大数据环境中自愿接种策略及个体安全保护方法研究

丁宏 牛文芳 王震 任一支 吴铤

摘要 大数据背景下，如何充分利用数据分析、挖掘等方法有效发现传染病传播规律，对于疾病防控、个体的安全保护有着重要作用和意义.自愿接种是对群体获得广泛免疫和安全保护的有效方式.以往的研究中，个体根据以往传播过程中的患病风险或者收益来确定是否进行自愿接种，如个体与其邻近的邻居比较上一个季节获得的收益来决定是否采用邻居的策略，也就是说策略更新对于群体的安全保护至关重要.本文研究了不同的策略更新方式对自愿接种行为的影响.通过比较个体采用不同的策略更新方式所获得的群体平均接种比例、疾病暴发规模和社会总花费，研究并设计出合理的策略更新方式，即在花费成本比较低的情况下，获得比较大的群体平均接种比例和较小的疾病覆盖率.

关键词 大数据；复杂网络；自愿接种；策略更新；安全保护

中图分类号TP311；O157.5

文献标志码A

0 引言

在大数据背景下，当传染病在人际网络中传播的时候，个体倾向于通过社交媒体的报道来获取疾病传播的相关数据信息[1].媒体报道当前的疾病传播情况时，尽早地提供关于疾病感染、疫苗接种、死亡率和病发率的数据消息，可以显著地降低疫情的严重程度.所以，当社交媒体报道关于疾病的相关数据信息时，也要快速地对数据进行处理分析.随着数据存储成本的迅速降低和通信网络带宽的不断提高，使大数据的发展变得更加容易.通过對疾病感染大数据的收集、存储和处理分析，及时地提供给群体有效的信息，有利于抑制疾病传播[2].同样，是否接种疫苗可以通过关于疫苗接种的研究决定，其实也取决于常规数据的检测.通过对疫苗接种相关的大数据分析，利用数据中有价值的情报，可以评估患病风险和接种成本等各种因素之间的关系，以制定有效的预防流感疫情的控制策略，提高种群的接种比例，降低种群的接种成本和患病风险，优化配置有限的公共卫生资源.

对于很多像天花、疯麻疹和禽流感病毒这类传染病，自愿接种对在疾病传播中获得广泛的免疫覆盖率有重要作用[3].但是在自愿接种行为中，个体会衡量患病风险和接种疫苗花费的成本.在人群中进行自愿接种以实现群体免疫是预防传染病大面积蔓延的有效手段，但却时常会导致公共物品困境[4].因为随着免疫覆盖率的增加，当群体免疫覆盖率达到一定程度时，群体中的个体即使不接种也不会被疾病传播，这时免疫覆盖率称为群体免疫值[5].

在复杂网络中传染病传播的研究中，关于自愿接种已经有很多人做出了努力.比如，Zhang等[6]探究了在流感传染病中自愿接种的影响，他们发现，除非给接种策略提供激励机制，否则接种行为不能阻止传染病的传播.实际上，个体只会被他邻居中的感染者感染.通常情况下，个体通过从邻居中获得的对患病和接种风险的感知来衡量自己的收益以及进行免疫决策.比如，Perisic等[7]已经探究出在自愿免疫情况下，当传染病传播时，个体会在接种所获得的收益大于不接种所获得收益的情况下选择接种.另外，研究者已经发现，对于个体而言，通过与邻居的接触而获得的一些适应接种行为的演化策略，如模仿[8]、相互比较[9]、生-死和死-生策略[10].在这个演化过程中，个体采用一种单纯的接种策略，通过社会学习和他上一次传播过程中获得的经验而决定是否接种或者是不接种.

当一个传染病传播季节结束后，个体根据上一个传播季节中的患病风险或收益进行策略更新以确定在下一个传染病传播季节如何进行免疫决策.在第一个工作中，主要是研究了在locally-mixed networks中的自愿接种行为，论文中提出了一种新的策略更新模型.整个模型主要包括以下几部分：首先，为了反映出接种的意愿，个体随机初始化他们接种的概率；另外，在免疫决策时，个体把与自己直接接触的邻居看成locally-mixed networks，依照传染病模型和邻居的接种策略，来预测自己的患病风险；根据患病风险，个体会平衡自己的患病代价和接种成本来更新自己的接种概率.该模型将会为分析个体自愿接种行为提供一个新的视角，这个角度没有依靠邻居之间的相互学习和上一个传染病季节传播过程关于接种和患病的经验.

本文主要研究不同的策略更新方式对自愿接种行为的影响.模型将从以下几个方面研究：首先，在整个演化过程最开始的时候，个体初始化自己的接种策略，即采用单纯的策略初始化（群体中有0.5的个体选择接种，有0.5的个体选择不接种）或者采用混合策略进行初始化（即每个个体取一个随机数p代表自己的接种意愿，然后再通过取随机数决定是否接种）.其次，当一个传染病传播季节结束后，每个个体进行策略更新，个体选择策略更新方式有下面几种：1）用费米方程（Fermi function，Fermi）[11-12]进行策略更新；2）用模仿接种行为（Imitation vaccination behavior，Imitation vaccination）[13]；3）用在locally-mixed networks中自我组织的接种策略（Self-organizing vaccinating strategy in locally-mixed networks，Self Vacstr in Local）进行策略更新；4）用在locally-mixed networks中自我组织的行为（Self-organizing behaviors in locally-mixed network，Self Behav in Local）进行策略更新.最后，比较几种策略更新方式对自愿接种行为的影响，看一下哪种策略更新方式在花费较小的情况下，能达到较高的接种水平.通过这样做，本文将分析出不同策略更新方式的优势，并在自由接种情况下，选择一种最优的策略更新方式，这对控制传染病以及维护社会安全有很大的意义.

1 模型

1.1 模型和方法

在有结构的群体中，本文的模型分为2个阶段来模拟个体的自愿接种动力学.第1个阶段是公共接种阶段，公共接种阶段发生在任何感染之前.在这个阶段，每个个体决定自己是否接种，接种需要花费的成本v.为了简单起见，假设对于每个接种的个体，能够获得一个完全的免疫力，在疾病传播过程中不会被感染.在每个传染病季节来临的时候，个体会初始化自己的接种策略，在每个传染病季节结束的时候，个体需要根据上一个季节接种的风险或者是收益来进行策略更新，决定下一个季节是否接种，策略更新的几种方法详见1.2.

第2个阶段是疾病传播阶段.在传播过程中，首先确定一个最初的感染数目I0，疾病根据SIR模型[14]进行传播，每天的传播率为β，恢复率为γ.疾病会一直传播，直到群体中没有感染个体为止.当个体被感染疾病时，会花费一个感染疾病的成本i，设置一个相对成本值c=i/v（0最后，i取随机数，当随机数小于p就接种，否则不接种.

为了研究不同的策略更新方式对自愿接种的影响，我们将模型应用到scale-free中进行模拟.在实验开始的时候，个体采用不同的接种策略来初始化：其中Fermi和Imitation vaccination采用单纯的接种策略；Self Vacstr in Local和Self Behav in Local采用混合的接种策略，实验按照上述的2个阶段（先进行接种策略更新，再进行传播过程）进行模拟.为了使群体中的个体状态达到稳定，每一次实验要迭代3 000次，实验中的数据取100次的平均值.

2 结果

在scale-free网络中模拟个体的自愿接种行为，种群规模N=1 000，平均度k=4，传播率β为0.55[11]，在Fermi和Imitation vaccination中，选择强度α都等于1.我们将看一下，用4种模型进行策略更新的时候，在一个传染病传播季节中，群体中的平均接种比例V、疾病的暴发规模R和社会总花费SC（量值为CS）随着c的变化情况.其中

CS=疫苗接种人数×疫苗花费+感染人数×感染花费=疫苗接种人数×c+感染人数×1.

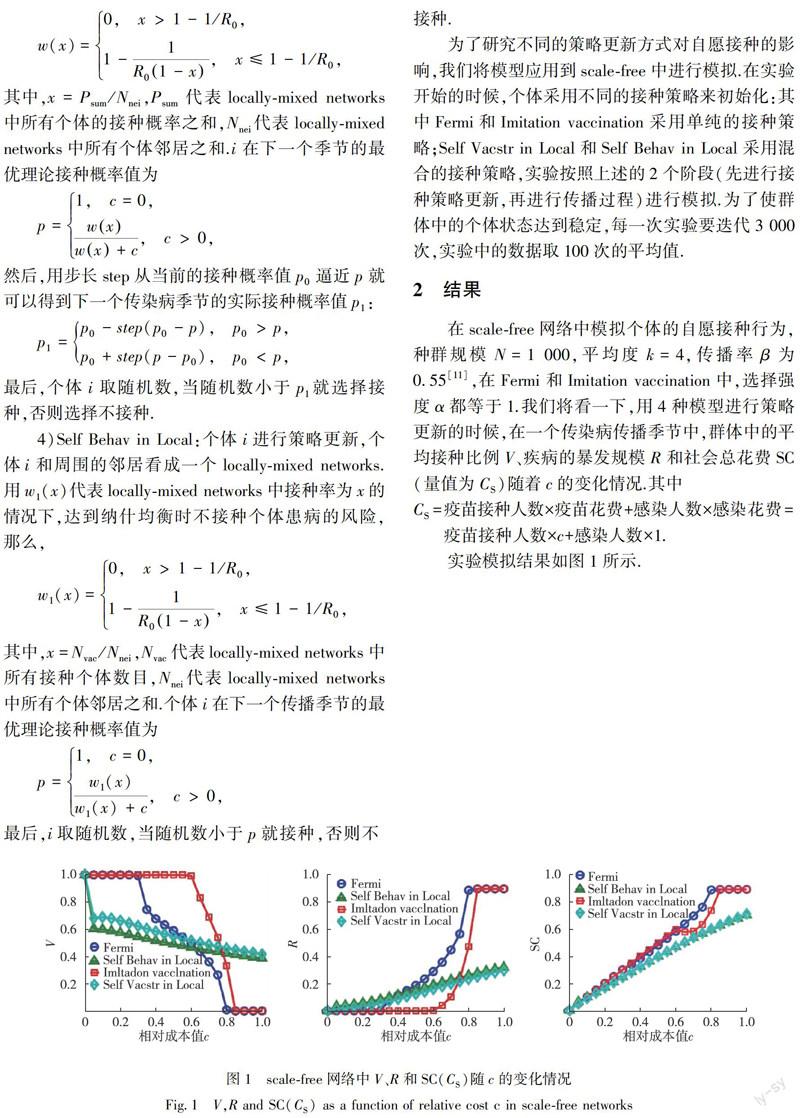
实验模拟结果如图1所示.

从图1中可以看出，用Self Behav in Local和Self Vacstr in Local进行策略更新时，随着相对成本值c的增加，社会总花费SC一直比用Fermi和Imitation vaccination进行策略更新要低.而且在相对成本值c较大的时候，用Self Behav in Local 和Self Vacstr in Local进行策略更新达到的群体平均接种比例V比较高，比如说，当c=1时，用Fermi和Imitation vaccination达到的平均接种比例V=0，而用Self Behav in Local和Self Vacstr in Local达到的平均接种比例V大约为0.4.虽然当相对成本值c较小的时候，用Fermi和Imitation vaccination达到的平均接种比例值V比较高，如当c=0.1时，用Fermi和Imitation vaccination达到的V=1，而Self Behav in Local和Self Vacstr in Local达到的平均接种比例分别是0.62和0.67左右，但是Self Behav in Local和Self Vacstr in Local达到疾病暴发规模R并不高，所以用Self Behav in Local和Self Vacstr in Local这2种策略更新方法的SC一直比较低.

当c=0.1时，用Self Behav in Local和Self Vacstr in Local达到平均接种比例值V比用Fermi和Imitation vaccination低，但是Self Behav in Local和Self Vacstr in Local达到疾病暴发规模R并不高.下面我们看一下，用这4种策略更新方法，在实验模拟过程中，易感染者S、感染者I、免疫者R和接种者V的随着迭代次数t的比例变化.

图2中第1行到第4行分别是用Fermi、Imitation vaccination、Self Vacstr in Local和Self Behav in Local進行策略更新时，第1、20、50、3 000个时间步steps中1 000个个体的S、I、R、V状态的变化情况，因为每个时间步steps代表一个传染病传播季节，而一个传染病季节结束的标志是群体中没有I个体，所以，图2中个体只有S、R、V 3种状态，其中S状态用蓝色表示，R状态用红色表示，V状态用绿色表示.从图2中可以看出，当c=0.1，用Fermi、Imitation vaccination进行策略更新时，当群体状态达到稳定时，所有的个体都变成了接种者（图2中绿色的点），用Self Vacstr in Local和Self Behav in Local进行策略更新时，当群体状态达到稳定时，群体中除了大部分的接种个体（绿色的点）以外，还有很多易感染者（蓝色的个体）和极少数目的免疫者（图2中红色的点），这就说明用Self Vacstr in Local和Self Behav in Local进行策略更新时，虽然并不是所有的个体都接种，但是群体中的感染个体很少，没有接种的那部分个体大多数为易感染者S，这部分个体没有花费任何的接种成本和患病代价，所以整个群体中的社会总花费SC比用Fermi、Imitation vaccination小.

当c=1时，用Self Behav in Local和Self Vacstr in Local进行策略更新，将对整个群体更有利，因为群体中的平均接种比例V比较大，社会总花费SC比较低.下面看一下，平均接种比例V、疾病暴发规模R随迭代时间t的变化情况（图3），因为在传播过程中，群体中个体的状态很快就达到平衡状态.

从图3a中可以看出，用Imitation vaccination和用Fermi进行策略更新，群体中的平均接种比例V快速下降，并在t=90时降为0，相对应图3b的疾病患病规模R也达到了最大值0.893；而用Self Vacstr in Local和Self Behav in Local进行策略更新，在图3a群体中的平均接种比例V很快达到了平衡值0.42和0.38，相对应图3b中，疾病患病规模只达到0.22和0.25.总之，从图3中的结果可以明显看出，用Self Vacstr in Local和Self Behav in Local比用Fermi和Imitation vaccination进行策略更新对整个群体更有利，因为用Self Vacstr in Local和Self Behav in Local达到的接种比例V较高，社会总花费SC较低.

3 結束语

当传染病在社交网络中传播时，当一个传播季节结束后，个体会根据上一个传播季节中的患病风险或收益进行策略更新以确定下一个传播季节来如何进行免疫决策.在这篇文章中，主要研究了个体分别采用Fermi、Imitation vaccination、Self Vacstr in Local和Self Behav in Local进行策略更新，对自愿接种行为的影响.通过上述的实验结果可以看出，个体采用Self Vacstr in Local和Self Behav in Local比采取Fermi、Imitation vaccination更有利于群体中抑制疾病的传播：当c比较小的时候，虽然采用Self Vacstr in Local和Self Behav in Local获取的V并不是最高的，但是疾病覆盖水平R很低，社会总花费SC也比采用Fermi、Imitation vaccination低；随着c的增加，采用Fermi、Imitation vaccination所获得的V会迅速下降，疾病覆盖水平R会迅速上升，社会总花费SC持续上升，总是比采用Self Vacstr in Local和Self Behav in Local的SC要高；当c=1时，从实验结果中更可以看出，采用Self Vacstr in Local和Self Behav in Local可以达到很高的V以及较低的社会总花费SC.综上所述，在自由接种情况下，当一个传染病季节结束时，个体采用Self Vacstr in Local和Self Behav in Local比采用Fermi、Imitation vaccination更有利于达到较高的接种水平，社会总花费SC更少，更有利于抑制群体中疾病的传播.在自由接种情况下，通过分析不同的策略更新方式找到个体可以采用的最优策略更新方式，对控制传染病传播以及维护社会安全有很大的意义.

参考文献

References

[1] Mummert A，Weiss H.Get the news out loudly and quickly：The influence of the media on limiting emerging infectious disease outbreaks[J].PLOS ONE，2013，8（8）：e71692

[2] Lopez D，Gunasekaran M，Murugan B S，et al.Spatial big data analytics of influenza epidemic in Vellore，India[C]∥IEEE International Conference on Big Data，2014：19-24

[3] Bonanni P.Demographic impact of vaccination：A review[J].Vaccine，1999，17（sup3）：120-125

[4] Hardin G.Thetragedy of the commons[J].Science，1968，162（5364）：1243-1248

[5] Czapkowski B，Pitman J，Pugliese B，et al.Herd immunity and you[C]//Great Problems Seminar Posters，2009

[6] Zhang H F，Zhang J，Zhou C S，et al.Hub nodes inhibit the outbreak of epidemic under voluntary vaccination[J].New Journal of Physics，2010，12（2）：023015

[7] Perisic A，Bauch C T.Social contact networks and disease eradicability under voluntary vaccination[J].PLOS Computational Biology，2009，5（2）：e1000280

[8] Wells C R，Klein E Y，Bauch C T.Policy resistance undermines superspreader vaccination strategies for influenza[J].PLOS Computational Biology，2013，9（3）：e1002945

[9] Traulsen A，Nowak M A，Pacheco J M.Stochastic dynamics of invasion and fixation[J].Physical Review E：Statistical Nonlinear & Soft Matter Physics，2006，74（1 Pt 1）：011909

[10] Ohtsuki H，Hauert C，Lieberman E，et al.A simple rule for the evolution of cooperation on graphs and social networks[J].Nature，2006，441（7092）：502-505

[11] Shi B Y，Qiu H J，Niu W F，et al.Voluntary vaccination through self-organizing behaviors on locally-mixed social networks[J].Scientific Reports，2017，7（1）：2665

[12] Fu F，Rosenbloom D I，Wang L，et al.Imitation dynamics of vaccination behaviour on social networks[J].Proceedings Biological Sciences，2011，278（1702）：42-49

[13] Mbah M L N，Liu J Z，Bauch C T，et al.The impact of imitation on vaccination behavior in social contact networks[J].PLOS Computational Biology，2012，8（4）：e1002469

[14] Buehlmann M，Beitler A.Lecture with computer exercises：Modelling and simulating social systems with MATLAB[R].2011