纵掠管束湍流对流换热的数值实验及其关联式

杨 茉, 吕海涛, 赵有生, 陆廷康, 戴正华

(1.上海理工大学 能源与动力工程学院,上海 200093; 2.上海斯耐迪工程咨询有限公司,上海 200233;3.上海市浦东新区特种设备监督检验所,上海 200136)

纵掠管束湍流对流换热的数值实验及其关联式

杨 茉1, 吕海涛1, 赵有生2, 陆廷康3, 戴正华3

(1.上海理工大学 能源与动力工程学院,上海 200093; 2.上海斯耐迪工程咨询有限公司,上海 200233;3.上海市浦东新区特种设备监督检验所,上海 200136)

对圆管内和纵掠管束的湍流对流换热分别运用k-ε模型和雷诺应力模型(RSM)进行了数值模拟.数值模拟结果表明,采用现有的管内湍流换热实验关联式近似计算纵掠管束对流换热的偏差较大.通过数值模拟研究了不同节距、不同雷诺数Re时纵掠管束的对流换热规律,给出了纵掠管束流动换热的努塞尔数Nu与Re的数值实验关联式.

纵掠管束; 湍流; 对流换热; 数值模拟; 关联式

纵掠管束强制对流换热在工业上有广泛的应用,对其进行准确的计算具有重要价值.一些传热学教科书,例如,杨世铭与陶文铨[1]编著的《传热学》和《换热器设计手册》[2],将纵掠管束强制对流换热计算归入到非圆截面通道对流换热的计算中,推荐的方法是近似采用圆管内强制对流换热的实验关联式(D&B公式)[3],只是将D&B公式中的圆管直径用所谓的当量直径来代替.王鹏等[4]、Wang等[5]采用数值方法的研究表明,利用这种当量直径加圆管内对流换热计算公式的近似处理方法得到的矩形和三角形等非圆形截面通道的努塞尔数Nu存在较大误差.Wang等[5]通过数值实验进一步对方形截面、三角形截面等几种非圆截面通道中的对流换热给出了修正公式,可使其换热计算精度显著提高.但是,Wang等[5]是针对正多边形通道对流换热进行的修正,而对纵掠管束流动换热规律没有涉及.除了文献[1-2]推荐的这种当量直径加圆管内对流换热计算公式的近似处理方法外,还没有发现其他关于纵掠管束对流换热计算的研究成果公开发表.笔者对圆管和纵掠管束对流换热进行了数值模拟,对圆管内对流换热计算所获得的数值结果与D&B公式[3]的计算结果吻合得很好.但是,纵掠管束对流换热的数值结果与利用上述文献推荐的当量直径加管内对流换热D&B公式的方法得到的结果的最大相对误差可达到142.5%.笔者认为,纵掠管束对流换热计算一直沿用至今的当量直径加D&B公式的方法已不足以满足工程上对传热计算的更高要求,有必要给出更高精度的传热计算公式.现有的文献资料表明,采用数值模拟方法对流动和传热的计算结果与实验结果吻合得很好.如余徐飞等[6]对密集管束的流动换热进行了数值研究;刘丽娜等[7]针对突缩通道内的流动和换热进行了数值模拟;张光璐等[8]对横掠单管的对流换热进行了数值研究;而Li等[9-10]采用较新的数值方法(Lattice Boltzmann方法)对熔融问题和自然对流换热进行了数值模拟.这些数值模拟例子表明,计算机数值模拟技术已日臻成熟,数值结果是可靠的,能够用于指导工程实践.

本文采用数值方法,首先对圆管内湍流对流换热进行了数值模拟,并将数值模拟结果与经典的实验关联式(D&B公式)的计算结果进行了比较,两者吻合得很好,确认了所采用的数值模拟方法可靠.然后进一步通过数值模拟对纵掠管束湍流对流换热进行数值实验,给出了不同工况换热的Nu,并进行了数据处理,给出了数值实验关联式.

1 问题描述与数值方法

1.1 问题

研究纵掠管束换热情况,部分管束排列的截面示意图如图1(a)所示,抽象出的一个典型通道模型如图1(b)所示.取通道的当量直径d=4f/U,f为通道截面积,U为湿周.f=S1S2-πD2/4,U=πD.S1,S2为管中心间距;D为管道直径.取管长L=140d,以消除入口段和出口局部单向化边界条件对计算结果的影响,保证流动和传热达到充分发展.图1(b)中的a边取为恒壁温边界条件,b边取为对称边界条件.

采用液态水作为模拟工质.假设:a.流体为牛顿流体;b.流动为三维、定常、不可压缩湍流流动;c.不计重力等体积力的影响.

采用标准k-ε双方程湍流模型和雷诺应力模型(RSM)进行数值模拟.这两种模型的控制方程可参见文献[1].k为湍流脉动动能,ε为湍流脉动动能的耗散率.通道进口速度和温度均匀,出口取局部单向化条件.

图1 管束及流道截面示意图

1.3 网格独立性和可靠性验证

针对雷诺数Re=46 403的情况,采用雷诺应力模型计算管束对流换热,对网格独立性进行验证.如图2所示(见下页),当截面周向网格节点数n大于150时,计算结果与网格无关.

为了确认计算结果可靠,模拟了Re=13 368,25 666,38 115,50 568,62 998,75 364,99 588,124 101,共8组情况的圆管内对流换热,将得到的努塞尔数Nu与对应8组工况由D&B实验关联式求得的Nu进行对比,两者吻合得较好,最大偏差在11.9%之内,如图3所示.

图2 圆管内的Nu随周向网格节点数的变化趋势

图3 标准k-ε模型与RSM对圆管内换热的Nu模拟结果

Fig.3 Comparison ofNuin circular tube between the uses of standardk-εmodel and RSM

1.4 数值方法比较

为了选择合适的方法,本文通过模拟计算对比了k-ε模型和RSM在圆管内的Nu的结果,如图3所示.D&B公式为

Nu=0.023Re0.8Pr0.4

定理 1 设(U,A∪D)是一个覆盖决策系统,U={x1,x2,…,xn}, U/D={k=1,2,…,l}。 如果θ=1,则

采用RSM与标准k-模型模拟后,得到的圆管内Nu的计算结果的相对误差在5%以内,这说明RSM计算结果是可靠的.由于RSM中的主观因素较少,因此,在进行管束对流换热计算时,采用了RSM.数值计算方法为基于原始变量的有限差分控制容积方法,对流扩散项采用延迟修正的QUICK差分格式[11],并用SIMPLE方法处理压力与速度耦合.

1.5 数据处理

定义截面流体平均温度

(1)

式中:ρ为流体密度;u为流体来流速度;cp为流体比定压热容;T为流体温度;A表示异形截面通道的截面面积.

局部对流换热系数h定义为

(2)

式中:q为管壁热流密度;Tw为管壁温度.

局部换热努塞尔数定义为

(3)

式中,λ为流体热导率.

2 计算结果与分析

2.1 数值模拟结果与传统方法计算结果对比

数值研究了Re=15 055,29 056,42 480,55 497,68 354,81 231,94 370,107 702,121 152,这9组工况下纵掠管束的流动换热特性.充分发展截面的平均Nu与采用当量直径和D&B实验关联式求得的Nu如图4所示.

图4 RSM与实验关联式的Nu对比

由图4可见,模拟结果和经典实验关联式的最大相对误差为142.5%,最小相对误差为20.9%.

由以上的比较可以看出,对于纵掠管束湍流换热的数值模拟结果与采用当量直径和D&B公式的近似处理方法的计算结果相差很大.笔者认为,数值模拟方法对于纵掠管束湍流换热的模拟结果是可靠的,而经典实验关联式运用当量直径作为特征尺度的方法只是一种近似的处理.因此,有必要给出纵掠管束新的数值实验关联式.数值模拟结果与用D&B公式计算的具体数值如表1所示.

表1 RSM与实验关联式的Nu随Re的变化

2.2 纵掠管束对流换热的数值实验关联式

对表1的数据进行拟合,最大回归误差为4.95%,拟合公式为

Nu=(0.019 72Re0.8+88.882 95)Pr0.4,

Re∈(1×104,1.2×105)

(4)

式中,Pr为流体普朗特数.

图5给出了数值结果和拟合曲线.

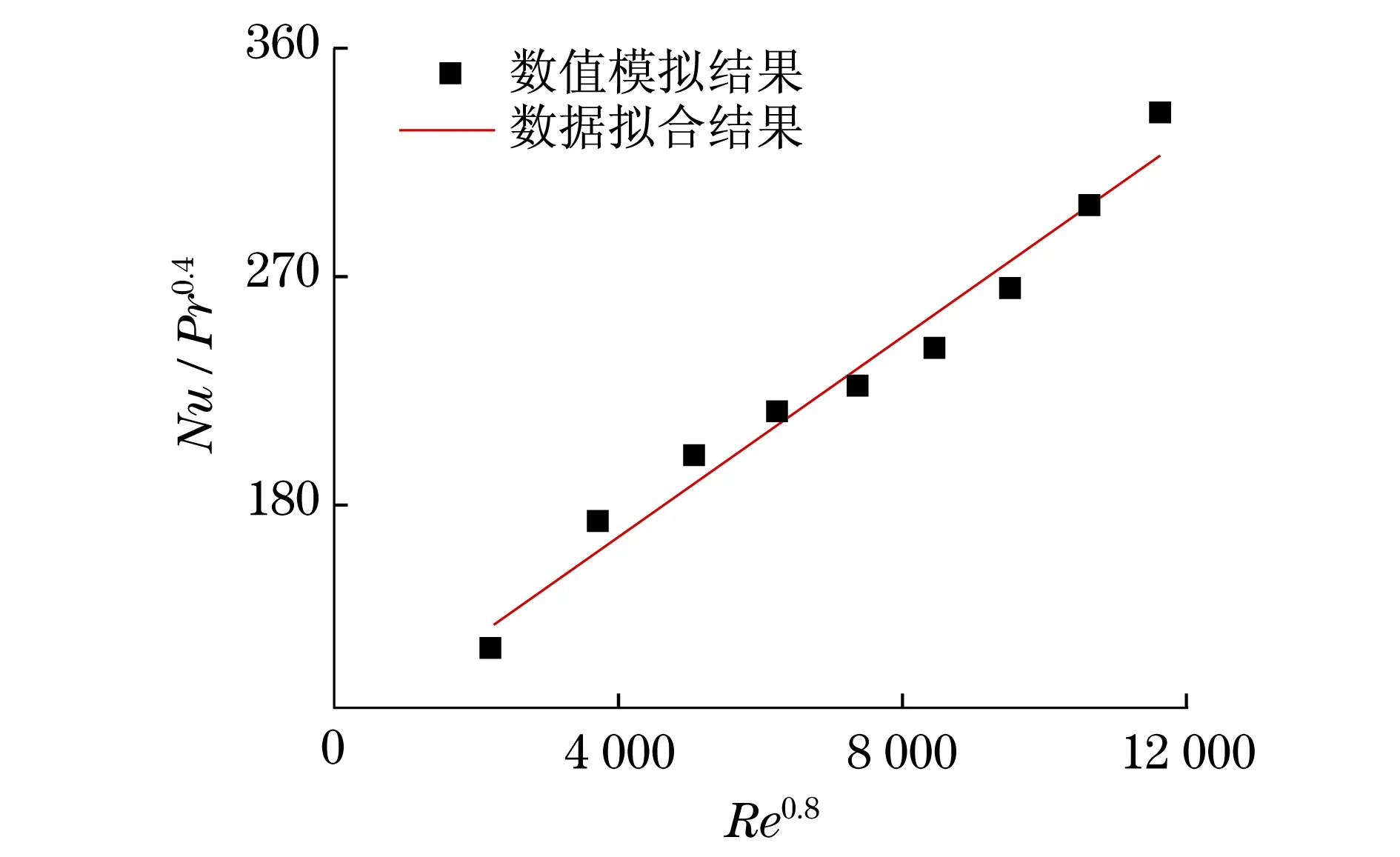
图5 数值模拟结果与数据拟合结果比较

本文对不同节距的情况进行了数值模拟,对结果进行了数据处理,并以式(4)为基础进行了修正.

Nu=C(0.019 72Re0.8+88.882 95)Pr0.4

(5)

其中,Re∈(1×104,1.2×105),C=0.99,m<4;C=0.91,m=4;C=1.066,4

3 结 论

以液态水为流动介质,利用雷诺应力模型对圆管纵掠管束湍流对流换热进行了数值模拟.对于圆形通道,数值模拟结果同已有文献的实验结果吻合得较好,验证了本文数值模拟结果的可靠性.在所计算的Re范围内,利用经典圆形通道湍流换热实验关联式计算纵掠管束对流换热系数的结果与数值模拟结果存在较大偏差,在本文的工况范围内,最高可达142.5%.提出了关于纵掠管束湍流对流换热的数值实验关联式,其中包括了管束节距变化的影响.

[1] 杨世铭,陶文铨.传热学[M].4版.北京:高等教育出版社,2006.

[2] 钱颂文.换热器设计手册[M].北京:化学工业出版社,2002.[3] DITTUS F W,BOELTER L M K.Heat transfer in automobile radiators of the tubular type[J].International Communications in Heat and Mass Transfer,1985,12(1):3-22.

[4] 王鹏,杨茉,王治云,等.非圆通道内变物性流体湍流换热的数值模拟[J].工程热物理学报,2014,35(11):2269-2273.

[5] WANG P,YANG M,WANG Z Y,et al.A new heat transfer correlation for turbulent flow of air with variable properties in noncircular ducts[J].Journal of Heat Transfer,2014,136(10):101701.

[6] 余徐飞,王治云,李起耘,等.横掠周期性密集管束流动换热的数值模拟[J].上海理工大学学报,2015,37(6):563-567.

[7] 刘丽娜,杨茉,王治云,等.扩缩通道内流动和换热非线性特性的数值模拟[J].上海理工大学学报,2015,37(5):440-444.

[8] 张光璐,李起耘,王治云,等.受限方腔内绕流两圆管强制对流换热的数值研究[J].上海理工大学学报,2015,37(6):551-556.

[9] LI Z,YANG M,ZHANG Y W.Numerical simulation of melting problems using the Lattice Boltzmann method with the interfacial tracking method[J].Numerical Heat Transfer,Part A:Applications,2015,68(11):1175-1197.

[10] LI Z,YANG M,ZHANG Y W.Lattice Boltzmann method simulation of 3-D natural convection with double MRT model[J].International Journal of Heat and Mass Transfer,2016,94:222-238.

[11] 杨茉,李学恒,陶文铨,等.QUICK与多种差分方案的比较和计算[J].工程热物理学报,1999,20(5):593-597.

(编辑:石 瑛)

Numerical Investigation and Correlation Formula on the Turbulent Convection Heat Transfer in Longitudinal Tube Banks

YANG Mo1, LÜ Haitao1, ZHAO Yousheng2, LU Tingkang3, DAI Zhenghua3

(1.SchoolofEnergyandPowerEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China;2.ShanghaiSnerdiEngineeringConsultingCo.,Ltd.,Shanghai200233,China; 3.ShanghaiPudongNewAreaSpecialEquipmentSupervisionandInspectionInstitute,Shanghai200136,China)

The turbulent convection heat transfers in a circular tube and in longitudinal tube banks were simulated with thek-εmodel and Reynolds stress model (RSM) respectively.The simulation results show that there are valid deviations in the approximate calculations by the existing experimental correlation formula for the turbulent convection heat transfer in longitudinal tube banks.Further simulations were carried out with different pitch ratios and Reynolds numbers.Based on the numerical simulation results,a new correlation formula was presented.

longitudinaltubebanks;turbulentflow;convectiveheattransfer;numericalsimulation;correlationformula

1007-6735(2017)02-0110-04

10.13255/j.cnki.jusst.2017.02.002

2016-04-24

国家自然科学基金资助项目(51476103);上海市教委科研创新项目(14ZZ134);上海市质量技术监督局公益科研项目(2012-41,2012-12)

杨 茉(1958-),男,教授.研究方向:传热数值技术.E-mail:yangm@usst.edu.cn

TK 124

A