三阶半线性中立型阻尼泛函微分方程的振动性
林文贤
(韩山师范学院数学与统计学院,广东潮州521041)
三阶半线性中立型阻尼泛函微分方程的振动性
林文贤
(韩山师范学院数学与统计学院,广东潮州521041)
研究了一类具有阻尼项的三阶半线性中立型泛函微分方程的振动性.通过引入参数函数和广义Riccati变换,结合积分平均技巧和一些分析技巧,建立了该类方程的所有解振动或收敛于零的若干新的充分条件,推广和改进最近文献的相应结果.
三阶中立型方程;半线性;阻尼项;振动性
近年来,泛函微分方程的振动性和渐近性研究开始受到关注,最近的成果可以参看文献[1-5].本文将考虑如下的一类三阶半线性中立型阻尼泛函微分方程
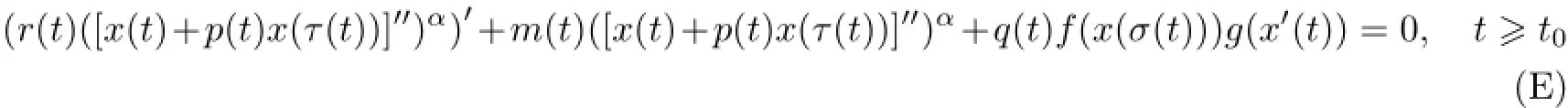
的振动性,其中α是两个正奇整数之比.假设下列条件成立.(H1)r(t),q(t)∈C([t0,∞),(0,∞)),p(t),m(t)∈C([t0,∞),[0,∞)),0≤p(t)≤p<1,且

(H2)τ(t),σ(t)∈C([t0,+∞),(0,+∞)),τ(t)≤t,σ(t)≤t,limt→∞τ(t)=limt→∞σ(t)=∞;K>0,u/=0,g(t)∈C(R,[L,+∞)),L>0.
引理1[6]设u(t)>0,u′(t)>0,u′′(t)≤0,t≥t0,则对任一λ∈(0,1),存在Tλ≥t0,使得

引理2[7]设u(t)>0,u′(t)>0,u′′(t)>0,u′′′(t)≤0,t≥Tλ,则存在β∈(0,1)和Tβ≥Tλ,使得

引理3[8]设A>0,B>0,X≥0,
引理4设x(t)是方程(E)的最终正解,令

则y(t)只有下列两种可能,即存在T≥t0,使得当t≥T时,有
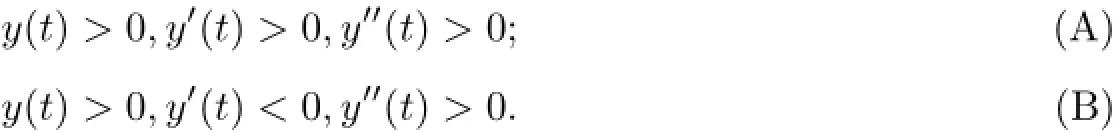
证明设x(t)是方程(E)的最终正解及条件(H3),则存在t1≥t0,当t≥t1时,有x(t)>0,x(σ(t))>0,x(g(t))>0.易知.y(t)>x(t)>0且
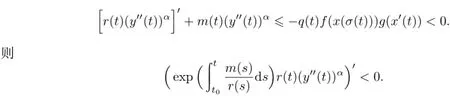
如果y′′(t)<0,则存在常数M>0,使得

在[t2,t)上对上式积分,有

上式中令t→∞,利用(H1),有y′(t)→-∞,因此,y′(t)最终为负.但是,由y′(t)和y′′(t)最终为负,可知y(t)最终为负,此与y(t)>0的假设矛盾,故有y′′(t)>0.因此,y(t)只能有(A)和(B)两种类型.引理4证毕.
引理5设x(t)是方程(E)的最终正解,且相应的y(t)为(B)型.若
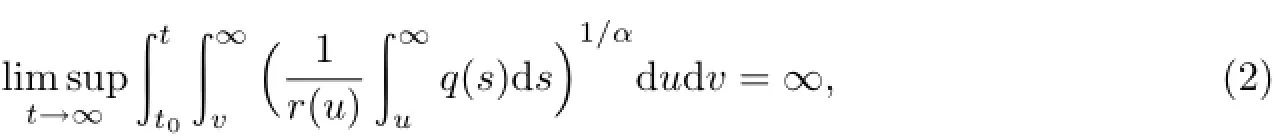
则limt→∞x(t)=limt→∞y(t)=0.
证明设x(t)是方程(E)的最终正解,且相应的y(t)为(B)型,存在常数l≥0,使得limt→∞y(t)=l.可以断言l=0.事实上,若l>0,则对任意ε>0,存在t2>t1,使得l<y(t)
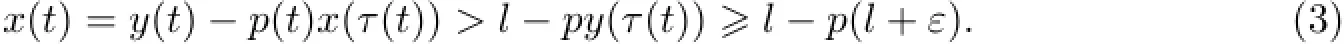

联合(H3)、(H4)、(4)式和方程(E),得
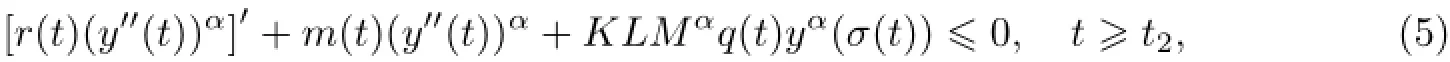
(5)式可写成

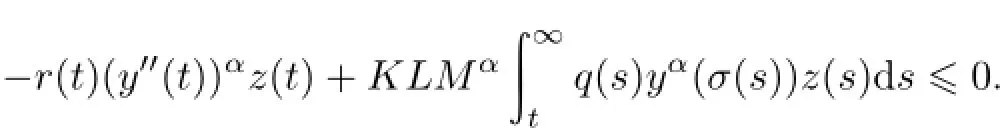
注意到y(σ(t))>l,t≥t3≥t2,z′(t)≥0,有
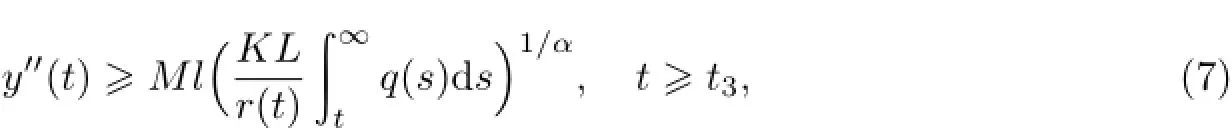
从t3到t对(7)式积分,得到

上式与(2)式矛盾.因此,l=0.又由于0<x(t)≤y(t),于是有limt→∞x(t)=0.引理5证毕.
定理1设n>1,且(2)式成立.若存在函数ρ∈C1([t0,∞),(0,∞)),使得
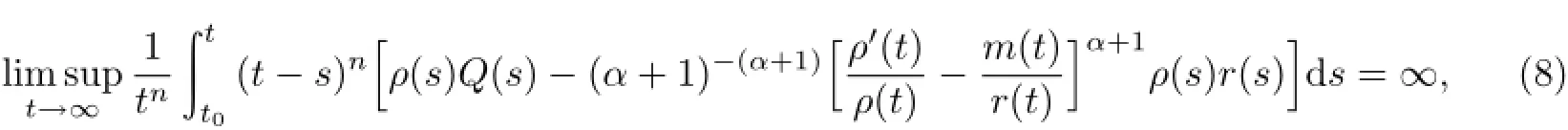
则方程(E)的每一解x(t)振动,或者当t→∞时x(t)→0,其中
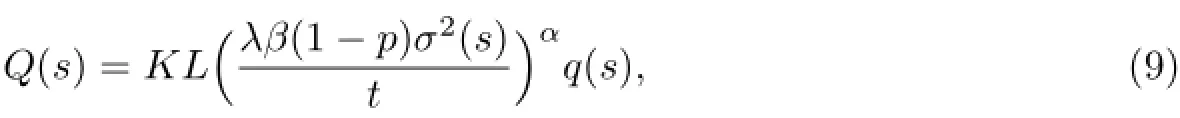
这里的α和β由引理1和引理2定义.
证明设方程(E)存在非振动解x(t),不失一般性,设x(t)最终为正(当x(t)最终为负时可类似证明),故存在充分大的t1≥T(T在引理1中提及),使得当t≥t1时有x(t)>0,x(τ(t))>0,x(σ(t))>0.y(t)由(2)式定义,由引理3,y(t)可能为(A)型或(B)型.
假设y(t)为(A)型,则有x(t)=y(t)-p(t)x(τ(t))≥y(t)-py(τ(t))≥(1-p)y(t).故由(H3),(H4)和(E),得
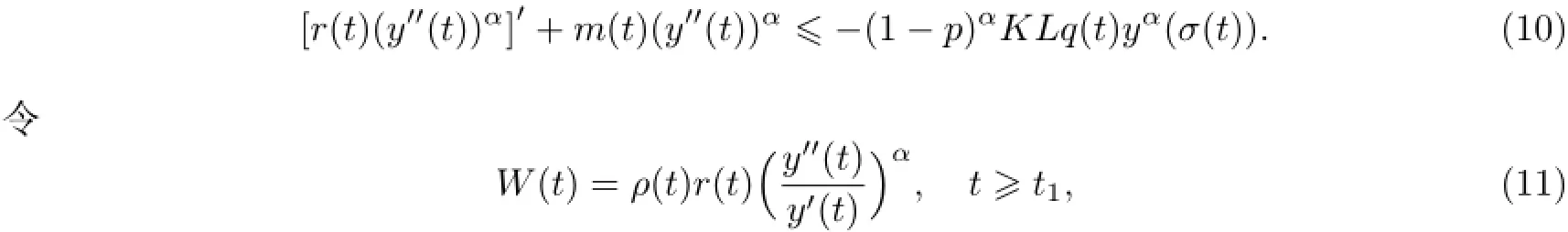
则由引理2和引理3得到

其中Q(t)由(9)式定义.
由引理4得
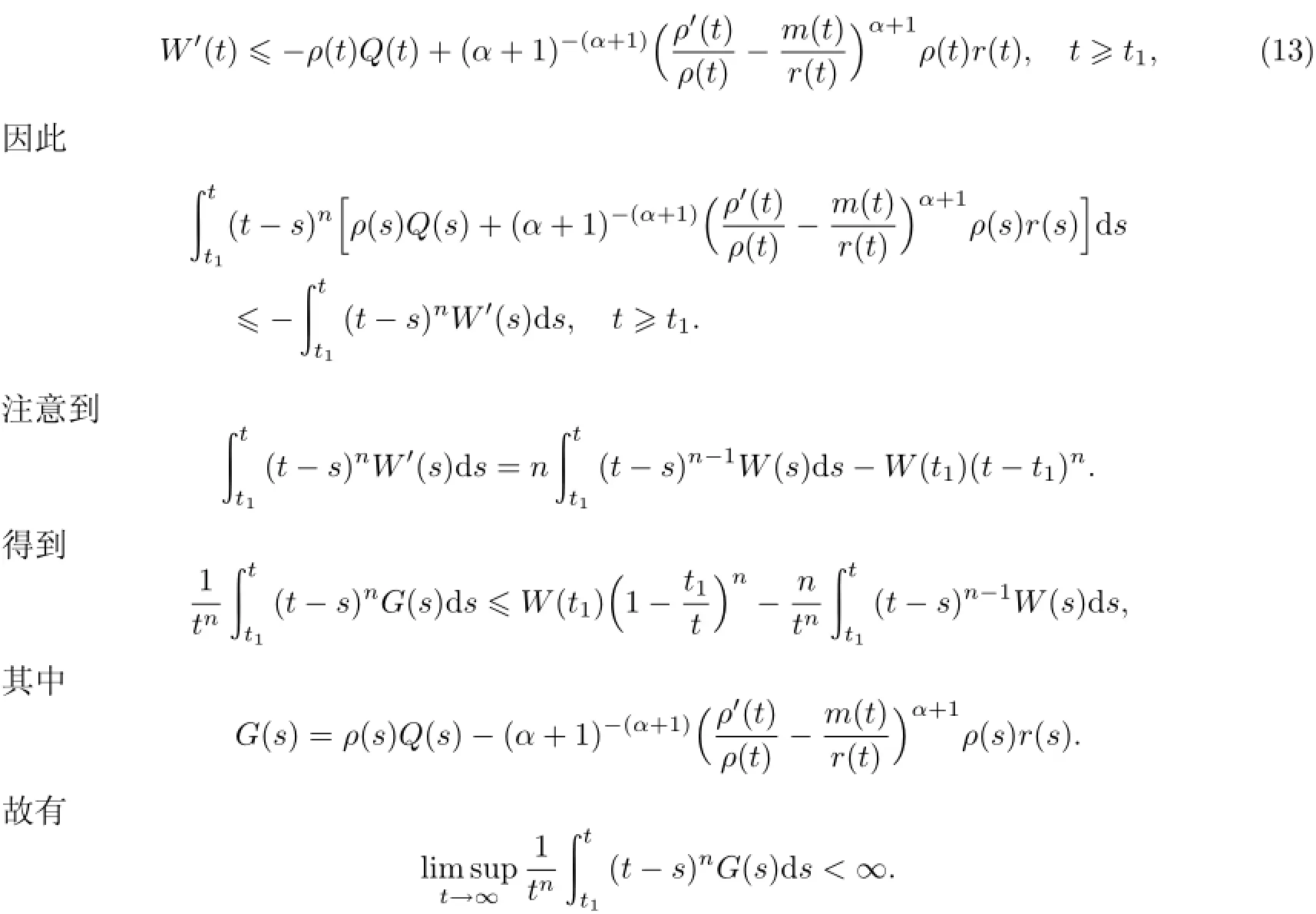
上式与条件(8)矛盾.
假设y(t)为(B)型,则由引理5有limt→∞x(t)=limt→∞y(t)=0.定理1证毕.
令D={(t,s)|t≥s≥t0},D0={(t,s)|t>s≥t0}.函数H(t,s)∈C(D,R)称为属于℘类,记作H∈℘,如果
(i)H(t,t)=0,t≥t0,H(t,s)>0,(t,s)∈D0;
定理2设(2)式成立,且存在函数H∈℘和ρ∈C1([t0,∞),(0,∞)),使得
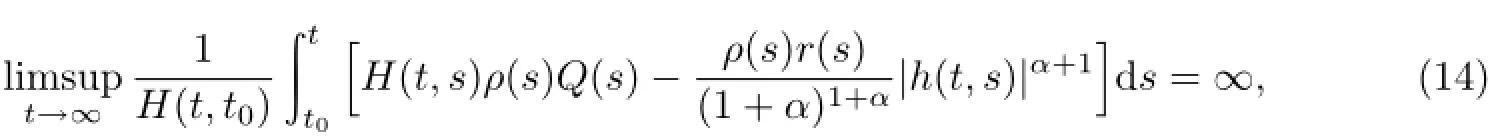
其中Q(s)由(5)式定义,则方程(E)的每一解x(t)振动,或者当t→∞时x(t)→0.
证明如同定理1的证明,设x(t)是(E)的非振动解,不妨设x(t)>0,x(τ(t))>0,x(σ(t))>0,y(t)由(2)式定义.由引理3,y(t)可能为(A)型或(B)型.
若y(t)为(A)型,定义函数W(t)如同(11)式,则W(t)>0且(12)式成立.令
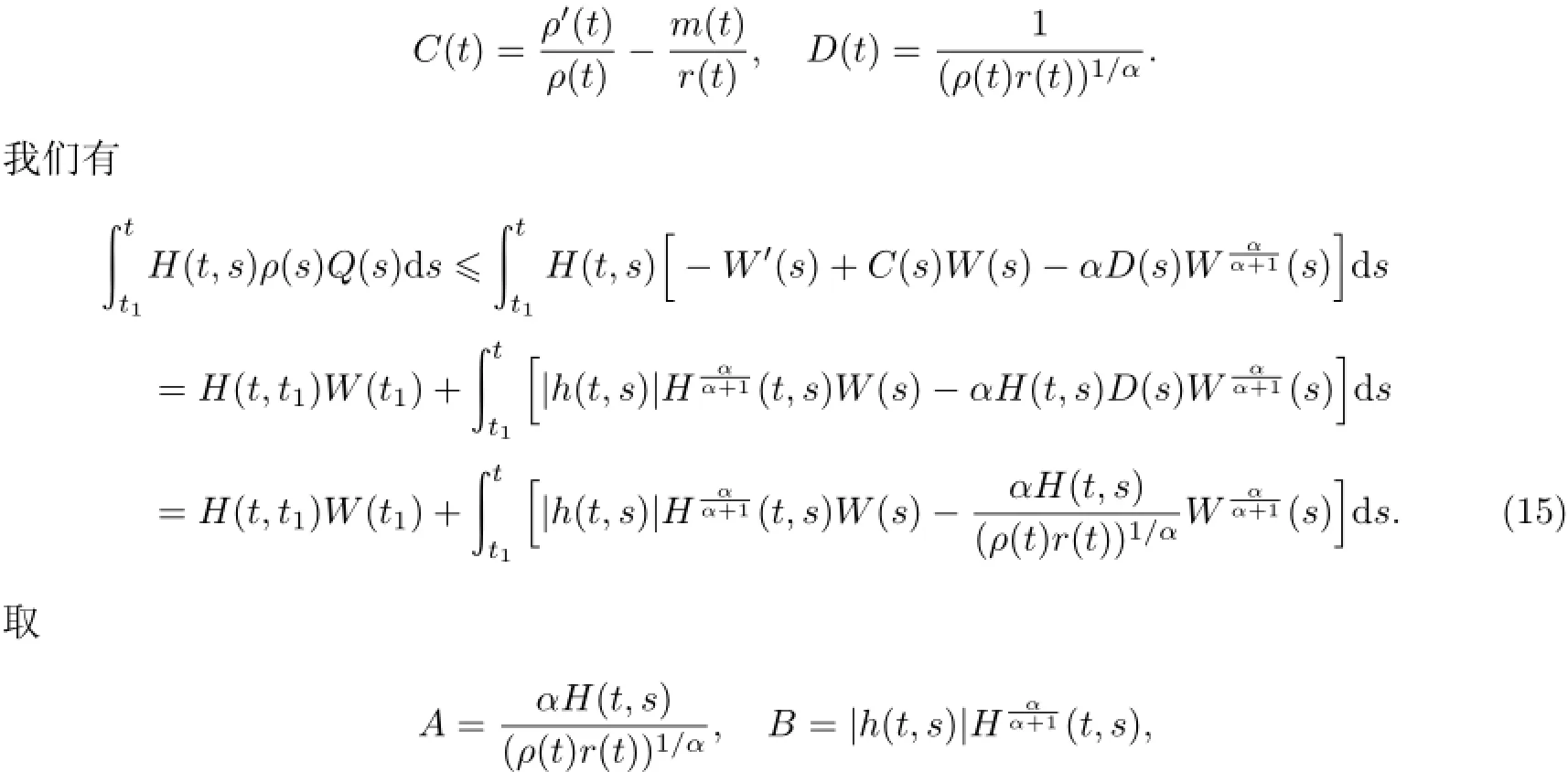
利用引理3,有
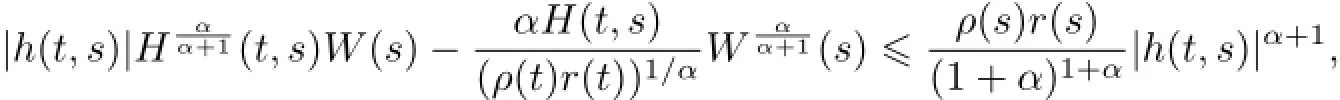
则由(15)式得
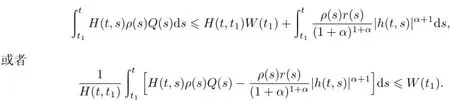
这与条件(14)矛盾.
如果y(t)为(B)型,证明与定理1的第二部分的证明一样,故省略.定理2证毕.
注当m(t)=0,α=1时方程(E)就是文献[5]所研究的方程,因而本文的结论推广和改进了文[5]的相应结果.
[1]DZURINA J.Asymptotic properties of the third order delay di ff erential equations[J].Nonlinear Anal TMA, 1996,26(1):33-39.
[2]GRACE S R,AGARWAL R P,PAVANI R,et al.On the oscillation of certain third order nonlinear functional di ff erential equations[J].Appl Math Comput,2008,202(1):102-112.
[3]TIRYAKI A,AKTAS M F.Oscillation criteria of a certain class of third order nonlinear deay di ff erential equations with damping[J].J Math Anal Appl,2007,325(1):54-68.
[4]AKTAS M F,TIRYAKI A,ZAFER A.Oscillation criteria for third-order nonlinear functional di ff erential equations[J].Appl Math Letters,2010,23(7):756-762.
[5]韩忠月.三阶非线性中立型泛函微分方程的振动性[J].华东师范大学学报(自然科学版),2012(1):113-120.
[6]ERBE L.Oscillation criteria for second order nonlinear delay equations[J].Canad Math Bull,1973,16(1):49-56.
[7]KIGURADZE I T.On the oscillation of solutions of the equation65(2):172-187.
[8]HARDY G H,LITTERWOOD J E,POLYA G.Inequalities[M].2nd ed.Cambridge:Cambridge University Press,1952
(责任编辑:林磊)
Oscillation of certain third-order half linear neutral functional dif f erential equations with damping
LIN Wen-xian
(College of Mathematics and Statistics,Hanshan Normal University,Chaozhou Guangdong521041,China)
This paper investigates the oscillation of third-order half linear neutral functional dif f erential equations with damping.By introducing parameter function and the generalized Riccati transformation and using integral averaging technique and some necessary technique,some new sufficient conditions which ensure that any solution of such equation oscillates or converges to zero were proposed.The corresponding results in literature are extended and improved.
third-order neutral equations;half linear;damping terms;oscillation
O175.1
A
10.3969/j.issn.1000-5641.2017.03.005
1000-5641(2017)03-0048-06
2016-09-18
广东省高等教育教学改革项目(GDJG20142396);广东省高等学校特色创新项目(2014GXJK 125);广东省自然科学基金(S2013010013372)
林文贤,男,教授,研究方向为泛函微分方程理论及应用.E-mail:linwx66@163.com.

