On modular representations of finite-dimensional Lie superalgebras
YANG Heng-yun,YAO Yu-feng
(Department of Mathematics,Shanghai Maritime University,Shanghai201306,China)
On modular representations of finite-dimensional Lie superalgebras
YANG Heng-yun,YAO Yu-feng
(Department of Mathematics,Shanghai Maritime University,Shanghai201306,China)
In this paper,we studied representations of finite-dimensional Lie superalgebras over an algebraically closed field F of characteristic p>2.It was shown that simple modules of a finite-dimensional Lie superalgebra over F are finite-dimensional,and there exists an upper bound on the dimensions of simple modules.Moreover,a finite-dimensional Lie superalgebra can be embedded into a finite-dimensional restricted Lie superalgebra.We gave a criterion on simplicity of modules over a finite-dimensional restricted Lie superalgebra g,and def i ned a restricted Lie super subalgebra,then obtained a bijection between the isomorphism classes of simple modules of g and those of this restricted subalgebra.These results are generalization of the corresponding ones in Lie algebras of prime characteristic.
Lie superalgebra;representation;p-envelope;p-character
0 Introduction
Recall that the finite-dimensional simple Lie superalgebras over the field of complex numbers were classified by Kac in the 1970s(cf.[1]).Furthermore,their representation theory was developed extensively.
In recent years,there has been an increasing interest in modular representation theory of restricted Lie superalgebras.A systematical research on modular representation theory was initiated and developed in[2-6]for Lie superalgebras of classical type,and in[7-15]for Lie superalgebras of Cartan type,respectively.W.Wang and L.Zhao[3]proved a super version of the celebrated Kac-Weisfeiler Property for the classical Lie superalgebras,which by def i nition admit an even non-degenerate supersymmetric bilinear form and whose even subalgebras are reductive.In[7-15],all simple restricted and some simple non-restricted modules of Lie superalgebras of Cartan type were classified.Moreover,character formulas for these simple modules were given.
In this paper,we study the modular representations of finite-dimensional Lie superalgebras.This research is largely motivated by[3,16,17].We brief l y introduce the structure of this paper.We collect the general notations and elementary preliminaries on Lie(associative) superalgebras in Section 1.Then Section 2 is devoted to developing general representation theory for a finite-dimensional Lie superalgebraover an algebraically closed field F of characteristicp>2.We show that each simple g-module is of finite-dimensional,and there exists an upper bound on the dimensions of simple modules.Moreover,g has a finitedimensionalp-envelope which is a restricted Lie superalgebra.In some sense,this helps us to reduce representations of finite-dimensional Lie superalgebras to those of restricted ones.We then study irreducible representations of finite-dimensional restricted Lie superalgebras in Section 3.We give a criterion for simplicity of an induced module of a finite-dimensional restricted Lie superalgebra g,and obtain a bijection between the isomorphism classes of simple modules of g and those of some restricted subalgebra(cf.Theorem 3.12).This reduces simple g-modules to those simple modules of a certain restricted subalgebra.
1 Notations and preliminaries
In this paper,we always assume that the ground field F is algebraically closed and of prime characteristicp>2.We exclude the casep=2,since in this case,Lie superalgebras coincide with Z2-graded Lie algebras.
1.1 Basic def i nitions
A superspace is a Z2-graded vector spaceV=V¯0⊕V¯1,in which we call elements ineven and odd,respectively.We usually write|v|∈Z2for the parity(or degree)ofv∈V,which is implicitely assumed to be Z2-homogeneous.A superalgebra is a Z2-graded vector spaceendowed with an algebra structure“·”such thatA superalgebrawith an algebra structure[-,-]is called a Lie superalgebra if for any homogeneous elementsx,y,zin g,the following conditions hold.

Homomorphisms of superalgebras(Lie superalgebras)are those linear mappings which reserve the Z2-grading and the superalgebra(Lie superalgebra)structure.
Example 1.1be a Z2-graded vector space over F with dimand dimV¯1=n.Then the algebra EndF(V)consisting of F-linear transformation ofVis an associative superalgebra with

Moreover,for any homogeneous elementsA,B∈EndF(V),we def i ne a new multiplication[-,-] by

Then(EndF(V),[-,-])is the so-called general linear Lie superalgebra,denoted by gl(V)=More precisely,

where Mati×jdenotes the set of alli×jmatrices fori,j∈N{0}.
Def inition 1.2be a Lie superalgebra.A Z2-graded vector spaceV=V¯0⊕V¯1is called a g-module if there exists a Lie superalgebra homomorphism from g to gl(V).
In this paper,all Lie superalgebras are assumed to be finite-dimensional.By vector spaces, subalgebras,ideals,submodules etc.,we mean in the super sense unless otherwise stated.
1.2 Key lemmas
In this subsection,we present several lemmas for later use.superalgebra.For elementsy,z1,···,znin A and
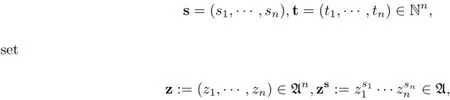
and
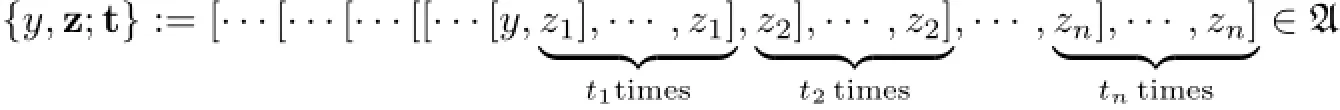
with the convention that{y,z;0}=y.Let


Lemma 1.3Assumeis an associative superalgebra.form+1≤i≤n.Then

ProofIt is trivial fors=0.In the following,we assumes/=0.Lx,Rxdenote the left and right multiplications byxin A,respectively.andLxcommutes with adx.We divide the proof into three cases.
Case 1sm+1=sm+2=···=sn=0.
In this case,we proceed by induction onm.The casem=1 follows from the following computation.
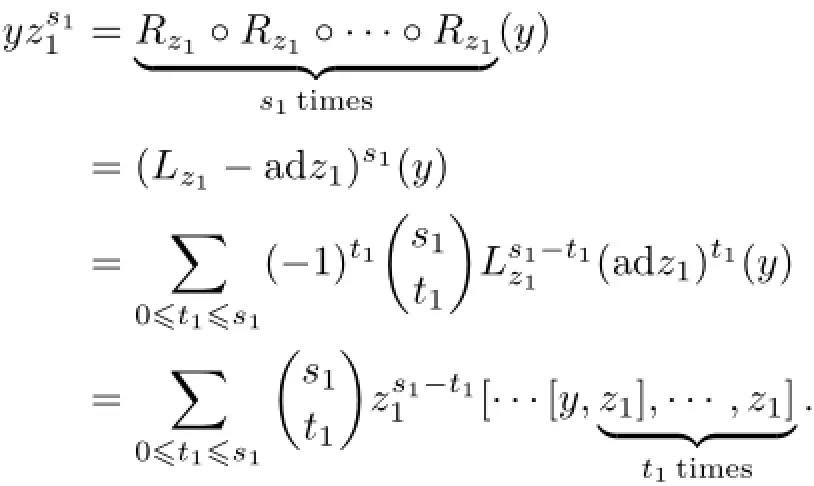
Assume thatm>1.The induction hypothesisyields

Hence,(1.1)holds in this case.
Case 2s1=s2=···=sm=0.
In this case,we proceed by induction onn-m.Ifn-m=1,then
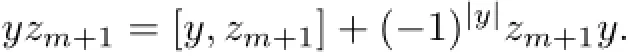
Hence,(1.1)holds in this case.Assume thatn-m>1.

The induction hypothesis yields

Hence,(1.1)holds in this case.
Case 3(s1,···,sm)/=0and(sm+1,···,sn)/=0.
Lets′=(s1,···,sm,0,···,0),s′′=(0,···,0,sm+1,···,sn).It follows from Case 1 and
Case 2 that

Hence,(1.1)holds in this case.
In conclusion,we f i nish the proof by the three cases above.
We have the following super version of Engel’s Theorem in Lie algebras.
Lemma 1.4LetV=be a fi nite-dimensional Z2-graded vector space and g⊆gl(V)be a Lie super subalgebra.Moreover,assume that g consists of nilpotent transformations. Then there exists a nonzero elementv∈such thatxv=0 for anyx∈g.
ProofWe proceed by induction onm.For the casem=0,the assertion follows from Engel’s Theorem(see[18]).Assume thatm=1 andnilpotent,-graded subspace.Moreover,it is easy to check that-submodule.By Engel’s Theorem again,subspace.Consequently,any nonzero homogeneous vectorvinsatisf i es the desired requirement.
Assume thatn>1 and the assertion holds for anym<n.We will show that it also holds form=n.For that,regard-module via adjoint action.Since
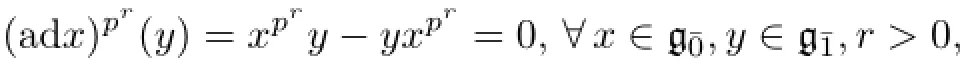
Let{x1,···,xl}be a homogeneous basis of g.Sincex1is nilpotent,andW3is invariant under the action ofx1,it follows thatis a nonzero Z2-graded subspace.For 2≤i≤l,de fi neinductively.These are nonzero Z2-graded subspaces by a similar argument.Then any nonzero homogeneous vectorvsatis fi es the requirement of the assertion.
As a consequence of Lemma 1.4,we get the following preliminary result on representations of Lie superalgebras.
Lemma 1.5vector space and g⊆L⊆gl(V)be Lie super subalgebras.Then the following statements hold.
(1)If[g,g]consists of nilpotent transformations and F contains all eigenvalues of elements in g,then there exists nonzerovsuch thatxv=λ(x)v,∀x∈g.
(2)Letλ∶g-→F be an eigenvalue function,i.e.,x-λ(x)idVis nilpotent for anyx∈g. Suppose thatλ(x)=0 for anyx∈[g,g].Thenλis linear.
(3)Keep assumptions as in(1).Moreover,assume that g is an ideal ofLandVis an irreducibleL-module.Then[g,g]=0,and anyx∈g has a unique eigenvalueλ(x)onV,andλ∶g-→F is linear.
Proof(1)According to Lemma 1.4,

Take anyxthen

Hence,W1is invariant under the actionMoreover,since
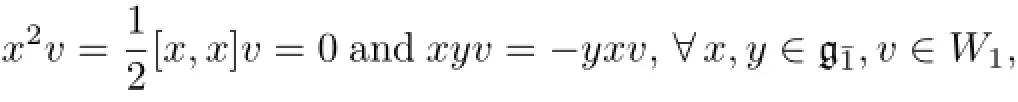
it follows that

(2)By(1),there existsvsuch thatxv=λ(x)v.Since the left hand side is linear inx,so is the right hand side.
(3)By(1),there existsv∈such thatxv=0,∀x∈[g,g].SinceVis an irreducibleL-module,V=U(L)v.Consequently,[g,g]acts trivially onV,since g is an ideal ofL.This means that[g,g]=0.is a nonzeroL-submodule.The irreducibility ofVas anL-module implies thatVcoincides withV,i.e.,x-λ(x)idVis nilpotent.Hence,λ(x)is the unique eigenvalue ofx.On the other hand,for anyx
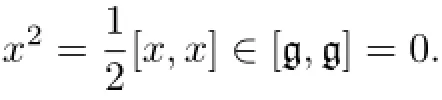
This implies that any elementis nilpotent,and 0 is the unique eigenvalue.The assertion thatλis linear follows from(2).
1.3 Restricted Lie superalgebras
The following def inition is a generalization of the notion of restricted Lie algebras[17,19]to the case of Lie superalgebras.
Def i nition 1.6[20]A Lie superalgebraa restricted Lie algebra and g¯1is a restricted g¯0-module under the adjoint action.This isequivalent to saying that there exists a so-calledp-mapping[p]on g¯0such that the following properties hold∶
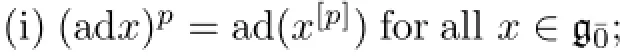
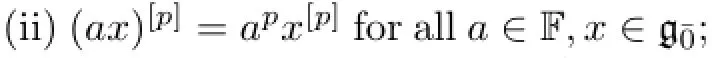
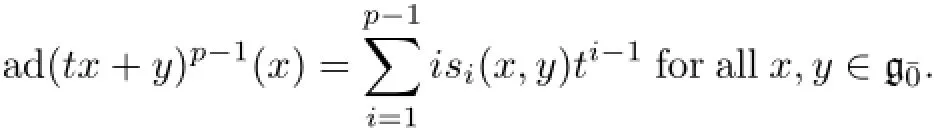
Heretis an indeterminate.
Remark 1.7Let(g,[p])be a restricted Lie superalgebra.Setξ(x)∶=xp-x[p]∈U(g)forAccording to Def i nition 1.6(i),ξ(x)∈Z(g)for anyMoreover,ξ∶isp-semilinear,i.e.,ξ(ax+by)=apξ(x)+bpξ(y),∀x,y∈
Example 1.8 Letg=gl(m|n)be the general linear Lie superalgebra.Let[p]∶
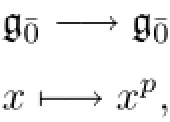
Proposition 1.9Let g be a restricted subalgebra of a restricted Lie superalgebra(G,[p]). Let[p]′∶g¯0-→g¯0be a mapping.Then the following statements are equivalent.
(1)[p]′is ap-mapping on g.
(2)There exists ap-semilinear mappingf
Proof(1)=⇒(2).Set

Since

factually mapsanda,b∈F,we have
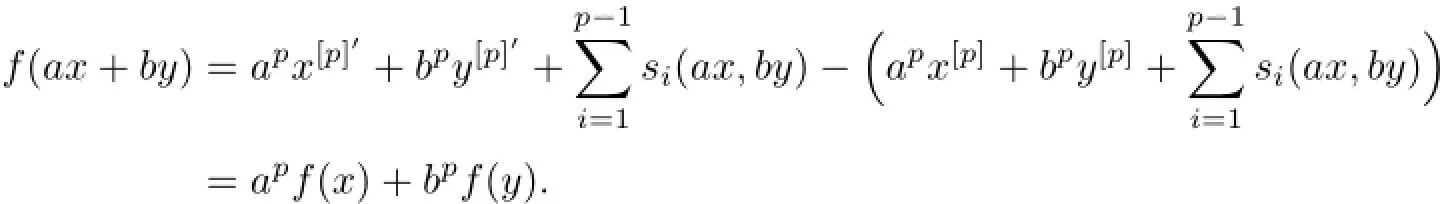
Consequently,fisp-semilinear.
(2)=⇒(1).We need to show that the three conditions in Def i nition 1.6 hold for[p]′.

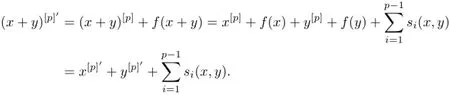
The proof is completed.
Let(g,[p])be a finite-dimensional restricted Lie superalgebra over F.LetZ0(g)be theF-algebra generated byxp-x[p]forx∈be the ideal inU(g)generated byxp-x[p]which is usually called the restricted enveloping superalgebra.
Suppose that{x1,···,xn}is a basisIt follows from the semilinearity ofξthatZ0(g)is generated byξ(x1),···,ξ(xn).Moreover,by PBW Theorem, we have
Proposition 1.10Keep notations as above,then the following statements hold.
(1)The elementsξ(x1),···,ξ(xn)are algebraically independent generators forZ0(g),i.e.,Z0(g)=F[ξ(x1),···,ξ(xn)]is a polynomial algebra ofnindeterminates.
(2)The universal enveloping superalgebraU(g)is free overZ0(g)with basis

(3)The restricted enveloping superalgebrau(g)is finite-dimensional,and has a basis

2 General representation theory
In this section,we always assume thata fi nite-dimensional Lie superalgebra over an algebraically closed field of characteristicp>2.We will show that each simple gmodule is finite-dimensional,and the dimensions of simple g-modules have an upper bound. Moreover,each finite-dimensional Lie superalgebra can be embedded into a finite-dimensional restricted Lie superalgebra.
Proposition 2.1be a finite-dimensional Lie superalgebra over an algebraically closed field F of characteristicp>2.Then the universal enveloping superalgebraU(g)is a finitely generatedZ(g)-module,andZ(g)is a finitely generated F-algebra.
Proof(1)Let{x1,···,xn}be a basis ofand{y1,···,ym}be a basis ofConsider

as elements in EndF(g).Since g is finite-dimensional,there existsdi∈N(1≤i≤n)such that

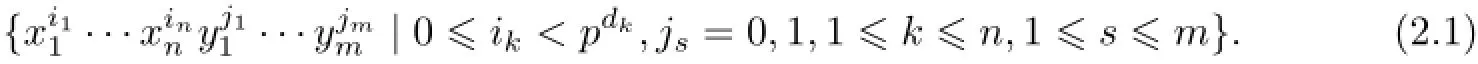
In particular,as aZ(g)-module,U(g)is spanned by those elements in(2.1).
(2)By(1),U(g)is a NoetherianO-module.Hence,as a submodule,Z(g)is also a NoetherianO-module.Consequently,Z(g)is a finitely generatedO-module.SinceOis finitely generated,it follows thatZ(g)is also finitely generated.
Theorem 2.2Let g=be a finite-dimensional Lie superalgebra over an algebraically closed field F of characteristicp>2.Then the following statements hold.
(1)Each irreducible representation of g is finite-dimensional.
(2)There exists a positive integerM(g)such that every irreducible representation of g has dimension less thanM(g).
ProofBy Proposition 2.1,we can assume thatLetVbe a simple g-module.Take a nonzero homogeneous elementvinV,then
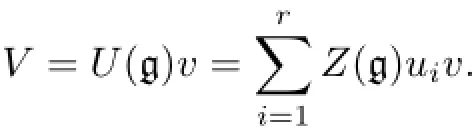
Hence,the moduleVis finitely generated overZ(g).SinceZ(g)is Noetherian,there exists a maximalZ(g)-submoduleV′⊂V.Consequently,Z(g)/m asZ(g)-modules for some maximal ideal m ofZ(g).Hence,mVSince mVis aU(g)-submodule ofVandVis irreducible,it follows that mV=0.Therefore,Z(g)acts onVasZ(g)/mproved.Moreover,by the discussion above,r+1 is an upper boundM(g).
Remark 2.3When g is a restricted Lie superalgebra,the results in Theorem 2.2 were asserted in[3].
Example 2.4be a subalgebra of gl(2|1)with{y},where
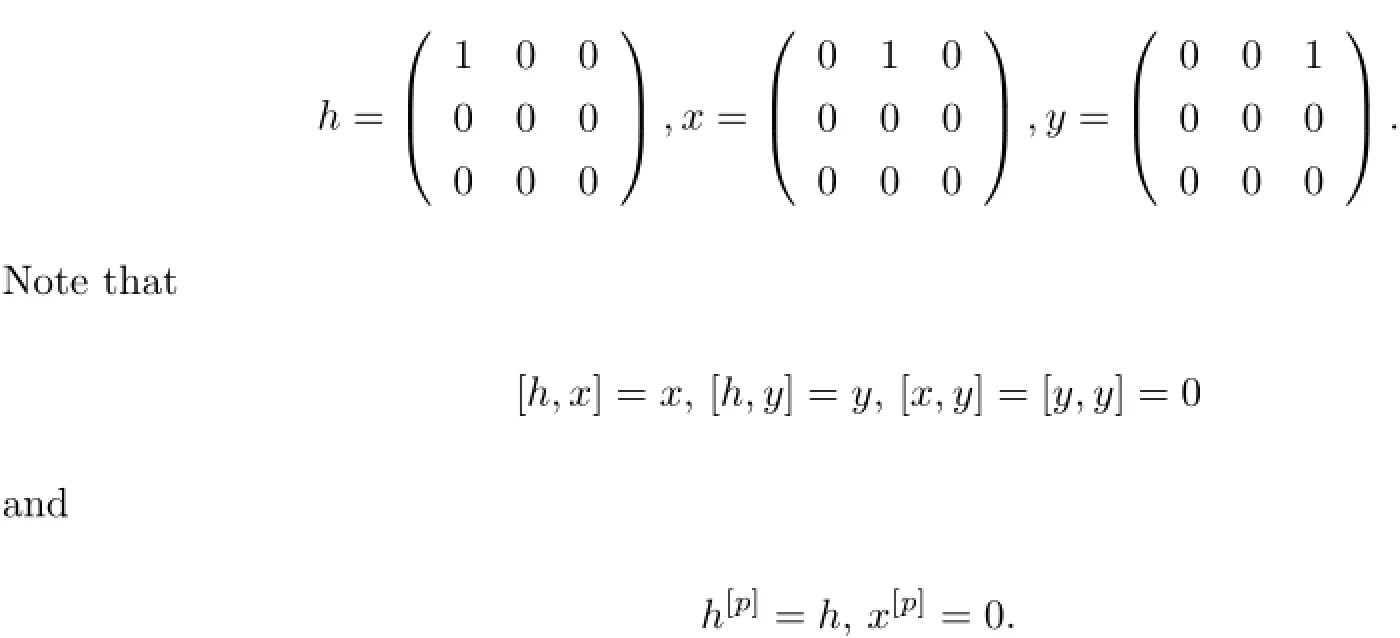
Hence,xpandhp-hare contained inZ(g).Consequently,
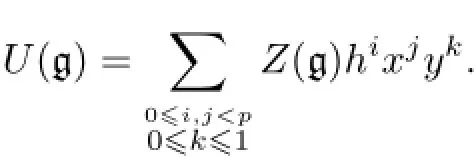
It is easy to check that
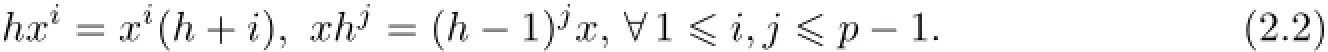
LetMbe an irreducible g-module.By Theorem 2.2,Mis finite-dimensional andxpacts as a scalar onM,sayingap.Hence,(x-a)p·M=(xp-ap)·M=0.
Case 1a=0.
Let g′=spanF{x,y}.Then g′is a subalgebra of g.According to Lemma 1.4,M′∶={m∈M|z·m=0,∀z∈g′}is a nonzero Z2-graded subspace.Moreover,M′is a g-submodule ofM,so thatM=M′by the irreducibility ofMas a g-module.Hence,Mis a simple module for the commutative Lie algebra g/g′Fh.Therefore,dimFM=1 andhacts as a scalar onM,whilex,yact trivially.Conversely,given any scalarb∈F,we get a one-dimensional simple g-module,denoted byMb,in whichhacts as multiplication byb,and g′acts trivially.
Case 2a/=0.

Setvi∶=hiBy(2.2),for 1≤i≤p-1,we have

It follows thatM′′∶=spanF{v0,v1,···,vp-1}is stable underxandh.We claim thatv0,···,vp-1are linearly independent.Suppose the contrary,then there exists somej<p-1 such thatM′′=spanF{v0,v1,···,vj}.It follows from(2.3)that tr(x|M′′)=(j+1)a.On the other hand,since[h,x]=x,we have tr(x|M′′)=0.This implies that(j+1)a=0,i.e.,j+1≡0(modp),a contradiction.Therefore,v0,v1,···,vp-1are linearly independent.Moreover,M′′is an irreducible g¯0-submodule,since up to scalars,v0is the unique eigenvector ofxWe have the following natural epimorphism of g-modules∶
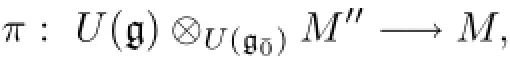
which is surjective by the simplicity ofMas a g-module.It is easyhas a unique maximal submoduley⊗M′′.dimFM=p.Conversely,givena,b∈F witha/=0,we have a simple g-moduleMof dimensionpwith basisv0,···,vp-1such thatyacts trivially,and the actions ofhandxare given as above.We denote this simple g-module byM(a,b).
In conclusion,{Mb,M(a,b)|a∈F×,b∈F}exhausts all non-isomorphic irreducible gmodules.
In the following,we study the connection of restricted and ordinary Lie superalgebras.
Def inition 2.5Let g=be a Lie superalgebra.
(1)A triple(G,[p],ι)consisting of a restricted Lie superalgebra(G,[p])and a Lie superalgebra homomorphismι∶g-→Gis called ap-envelope of g ifιis injective andG=ι(g)p, whereι(g)pdenotes the restricted subalgebra generated byι(g).
(2)Ap-envelope(G,[p],ι)of g is called universal,if it satisf i es the following universal property∶For any restricted Lie superalgebra(H,[p]′)and any homomorphismf∶g-→H, there exists a unique restricted homomorphismg∶(G,[p])-→(H,[p]′)such thatg◦ι=f.
The following result asserts that the universalp-envelope of a Lie superalgebra always exists and is unique.
Proposition 2.6Every Lie superalgebrahas a unique universalp-envelope
ProofLetbe the restricted subalgebra ofU(g)generated by g.LetHbe a restricted Lie superalgebra andf∶g-→Hbe a homomorphism.Recall thatHcanonically embedded intou(H).The universal property ofU(g)gives rise to an associative homomorphismTherefore,generated by g and thep-th powers,this extension is unique.The uniqueness offollows from the def i nition of the universalp-envelope.
Proposition 2.7Let g=be a Lie superalgebra.Then the following statements hold.
(1)If g is finite-dimensional,andis ap-envelope of g,thenis finitedimensional.
(2)If g is finite-dimensional,then g possesses a finite-dimensionalp-envelope.
(3)Each homomorphism of Lie superalgebrasf∶g-→h can be extended to a restricted homomorphism
Proof(1)Recall thatthe restricted subalgebra generated byι(g).Hence,

It is easy to check that Kerφ=Consequently,
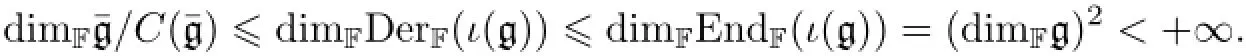
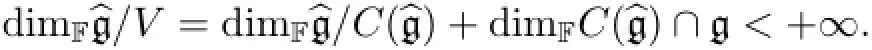
Then the restricted subalgebra generated by g inis the desiredp-envelope of g.

Iffis onto,thenIffis injective,it extends to an injective homomorphism
The following result is a superversion of Iwasawa’s Theorem in the case of Lie algebras.
Theorem 2.8be a finite-dimensional Lie superalgebra.Then g admits a finite-dimensional faithful representationρ.Moreover,assumethenρ(x)is nilpotent if and only if adxis nilpotent.
ProofWe first assume that g is restricted with thep-mapping[p].Without loss of generality,according to Proposition 1.9,we can assume that[p]|zg¯0(g)=0.This implies that adxis nilpotent if and only ifxis[p]-nilpotent forx∈Letρ∶g-→gl(u(g))be the left multiplication in the restricted enveloping superalgebrau(g).Thenρis a faithful representation of g,andxis[p]-nilpotent if and only ifρ(x)is nilpotnet.Consequently,adxis nilpotent if and only ifρ(x)is nilpotent.
In general,according to Proposition 2.7,there exists a finite-dimensionalp-envelope of g, denoted byG.By the discussion above,Gadmits a finite-dimensional faithful representationϱ∶G-→gl(V)with the desired property.Since adg(x)is nilpotent if and only if adG(x)is nilpotent forx∈Thus,ρ∶=ϱ|gsatisf i es the required property.
We have the following close connection between representations of a Lie superalgebra and itsp-envelope.
Theorem 2.9LetGbe ap-envelope of a finite-dimensional Lie superalgebra g andρ∶g-→gl(V)be a representation of g.Then there exists a representationextendingρ,and each g-submodule ofVis aG-submodule.
ProofThe statement obviously holds forG=the universalp-envelope of g.In general,by Def i nition 2.5,there exists an embeddingι∶g→Gand a restricted homomorphism
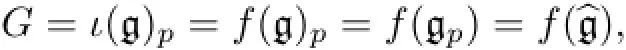
i.e.,fis surjective.We can fi nd a subspaceWofcontaining g such thatf|W∶W-→Gis an isomorphism(Wis indeed a subalgebra).is the desired representation ofG,whereis the restriction of the representation
According to Proposition 2.7,any fi nite-dimensional Lie superalgebra can be embedded into a fi nite-dimensional restricted Lie superalgebra.In the next section,we will study representations of restricted Lie superalgebras over a fi eld of prime characteristic.
3 Representations of restricted Lie superalgebras
In this section,we always assume that the base field F is algebraically closed of characteristicp>2,and g=is a finite-dimensional restricted Lie superalgebra over F with thep-mapping[p].
LetMbe a simple g-module.ThenMis finite-dimensional by Theorem 2.2.According to Schur Lemma,ξ(x)=xp-x[p]acts onMby a scalar for anyWe write this scalar asχM(x)pfor someχM(x)∈F.The semilinearity ofξimplies that
Theorem 3.1The functionχMis called thep-character ofM.More generally,ifVis a g-module andVhas ap-characterχif

In the following,when we writeχ∈g∗,we always make convention thatalso referχ∈as a linear function on g with
Proposition 3.3IfMhas ap-characterχandM′has ap-characterχ′,thenM∗has ap-character-χandM⊗M′has ap-characterχ+χ′.
The g-modules withp-character 0 are called restricted modules.They correspond to Lie superalgebra homomorphismsρ
Proposition 3.3Letχ∈and{y1,···,ym}is a basis of g¯1,then the superalgebraUχ(g)has the following basis
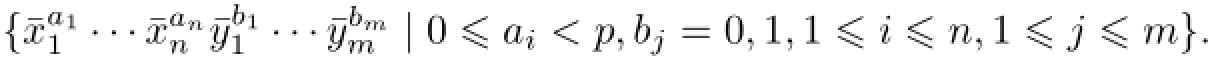
In particular,dimFUχ(g)=2dimFg¯1pdimFg¯0.
The following result asserts that the composition factors of a finite-dimensional indecomposable g-module have the samep-character.
Proposition 3.4Let g=be a finite-dimensional restricted Lie superalgebra over an algebraically closed field F,andMa finite-dimensional indecomposable g-module.Then there exists a uniquesuch that each simple composition factor ofMhas thep-characterχ.
ProofLetd=dimFM.Take a basis{x1,···,xn}of g¯0.Consideras a linear transformation onM.We can decomposeMas a direct sum of Z2-graded vector subspaces∶

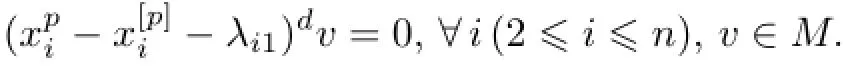

Consequently,each simple composition factor ofMadmits thep-characterχ.
As a direct consequence,we have
Corollary 3.5Let g=be a finite-dimensional restricted Lie superalgebra over an algebraically closed field,andVa finite-dimensional g-module.ThenVcan be decomposed into direct sum of submodules∶where the composition factors of eachhave the samep-characterχifor 1≤i≤t.Thoseχi(1≤i≤t)are called the generalizedp-characters ofV.
In the following,we always assume thatIis an ideal of a finite-dimensional restricted Lie superalgebrawithλ([I,I])=0.Let

which is a restricted subalgebra of g.Moreover,Iis also an ideal of gλ.
Let{z1,···,zl,zl+1,···,zr}be a cobasis of gλin g,wherel<j≤r.For a givenχ∈g∗(recall the convention that)and a finite-dimensional gλ-moduleMwith thep-characterχ|gλand

be the inducedUχ(g)-module.As a vector space,we have


We then have a f i ltration

We need the following lemma for later use.
Lemma 3.6Keep notations as above.
(2)For anyv∈M,s∈Nrwiths≾τ,we have
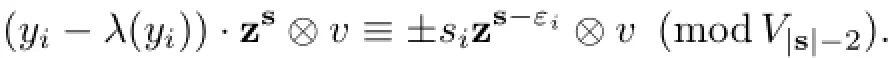
Proofforz∈g andy∈I.We then get a linear map
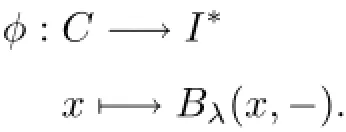
Thenφis injective.Consequently,φ(z1),···,φ(zr)are linearly independent.Hence,there existsy1,···,yr∈Isuch that

Sinceλ(g¯1)=0,we can choosey1,···,yl∈I¯0andyl+1,···,yr∈I¯1.
(2)According to Lemma 1.3,

Fort/=0,we have{yi-λ(yi),z;t}={yi,z;t}∈I,and{yi,z;t}⊗v∈1⊗M=V(0).Consequently,
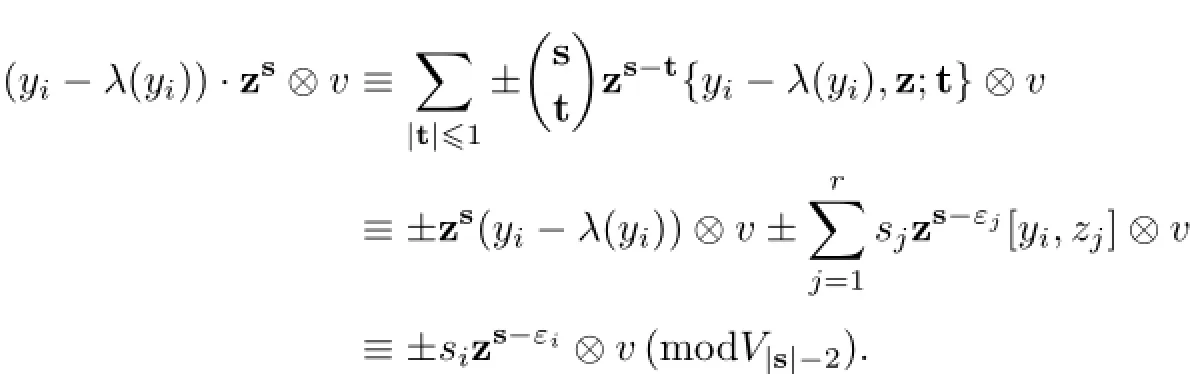
With aid of Lemma 3.6,we get the following result describing the submodule structure of the induced module
Proposition 3.7LetWbe a g-submodule of(M,χ).Then there exists a gλsubmoduleM′ofMsuch thatW∩(1⊗M)=1⊗M′and
ProofLetM′∶={v∈M|1⊗v∈W}.ThenM′is a gλ-submodule ofM.Moreover,W∩(1⊗M)=1⊗M′.Forj∈N,set

ThenW(0)=W∩V(0).We will show thatW∩V(j)⊆W(j)by induction onj.Letj≥1 and suppose thatW∩V(j-1)⊆W(j-1).Letv∈W∩V(j).Choose a cobasis{v1,···,vt}ofM′inM.Without loss of generality,we can assume that

whereas,k∈F fors≾τ,|s|≤jand 1≤k≤t.According to Lemma 3.6,we have
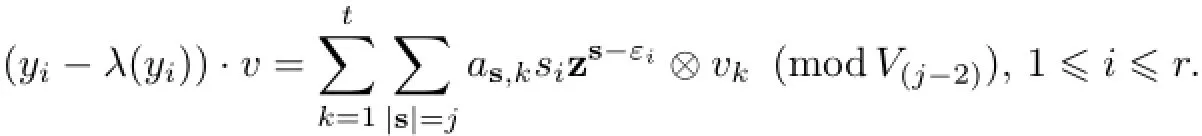
Hence,(yi-λ(yi))·v∈W∩V(j-1)⊂W(j-1).It follows from the def i nition ofW(j-1)thatsias,k=0 for|s|=jand 1≤i≤r,1≤k≤t.Consequently,v=0.This implies thatW∩V(j)⊆W(j).On the other hand,it is obvious thatW(j)⊆W∩V(j),so thatW∩V(j)=W(j),∀j≥0.Hence,W=W∩V=W∩V(p-2)l+r=W(p-2)l+r=Indggλ(M′,χ).
As a direct consequence,we have the following criterion on irreducibility of the induced
Theorem 3.8The inducedUχ(g)-moduleis irreducible if and only ifMis irreducible.
ProofThe sufficient implication is obvious.It suffices to show the necessary implication. Suppose thatMis irreducible.LetWbe a g-submodule ofBy Proposition 3.7, there exists a gλ-submoduleM′ofMsuch thatW=Consequently,W=0 or
For a g-moduleV,setVλ∶={v∈V|y·v=λ(y)v,∀y∈I},which is a gλ-submodule ofVby a straightforward computation.
Theorem 3.9Let g=be a finite-dimensional restricted Lie superalgebra over an algebraically closed field.LetVbe an irreducible g-module,andIbe an ideal of g.Then the following statements hold.
(1)IfVhas ap-characterχ∈g∗and there isλ∈I∗withλ([I,I])=0 andVλ/=0,thenandVλis an irreducible gλ-module.
(2)If[I,I]operates nilpotently onV,then there existsχ∈g∗,λ∈I∗withλ([I,I])=0
Proof(1)SinceVis irreducible,there existsχ∈g∗such thatVis a finite-dimensionalUχ(g)-module,and we have the following surjective homomorphism

Note that KerΨ is a g-submodule of(Vλ,χ)which intersects 1⊗Vλtrivially.This implies that KerΨ=0 by Proposition 3.7.Hence,Ψ is an isomorphism andVλis irreducible by Theorem 3.8.
(2)follows from Lemma 1.5 and the statement(1).
Remark 3.10IfI◃g is an abelian ideal,then Theorem 3.9(2)applies.
Def i nition 3.11LetVbe a g-module andI◃g be an ideal.We sayλ∈I∗a good eigenvalue function forVifλ([I,I])=0 andVλ/=0.
Letχ∈g∗andI◃g.Letλ∈I∗withλ([I,I])=0.We denote by Cχ,λ(resp.Dχ,λ)the set of isomorphism classes of irreducible g(resp.gλ)modules withp-characterχ(resp.χ|gλ) and a good eigenvalue functionλ.
Theorem 3.12Let g=g¯0⊕g¯1be a finite-dimensional restricted Lie superalgebra over an algebraically closed field.Letχ∈g∗.LetI◃g be an ideal andλ∈I∗withλ([I,I])=0. Then the following map

is bijective.
ProofBy Theorem 3.9,Υ is well-def i ned.Let

which is well-def i ned by Theorem 3.8.
LetMbe an irreducible gλ-module withp-characterχ|gλand a good eigenvalue functionThenVis irreducible by Theorem 3.8.Moreover,1⊗MLemma 1.5(3).Thanks to Theorem 3.9,Consequently,Vλ=1⊗Mby comparing their dimensions,i.e.,Υ◦Γ(M)
Conversely,letVbe an irreducible g-module withp-characterχand a good eigenvalue functionλ.ThenVby Theorem 3.9,i.e.,Γ◦Υ(V)~=V.Therefore,Υ is bijective,and Γ is its inverse map.
Example 3.13Let g=be the so-called Heisenberg Lie superalgebra withspanF{c},g¯1=spanF{xi,yj|1≤i,j≤n},and thep-mapping[p]and the Lie bracket subject to the following rules∶

[1]KAC V G.Lie superalgebras[J].Advances in Mathematics,1977,26(1):8-96.
[2]SHU B,WANG W Q.Modular representations of the ortho-symplectic supergroups[J].Proceedings of the London Mathematical Society,2008,96(1):251-271.
[3]WANG W Q,ZHAO L.Representations of Lie superalgebras in prime characteristic I[J].Proceedings of the London Mathematical Society,2009,99(1):145-167.
[4]WANG W Q,ZHAO L.Representations of Lie superalgebras in prime characteristic II:The queer series[J]. Journal of Pure and Applied Algebra,2011,215:2515-2532.
[5]ZHANG C W.On the simple modules for the restricted Lie superalgebra sl(n|1)[J].Journal of Pure and Applied Algebra,2009,213:756-765.
[6]ZHENG L S.Classical Lie superalgebras in prime characteristic and their representations[D].Shanghai:East China Normal University,2009.
[7]SHU B,ZHANG C W.Restricted representations of the Witt superalgebras[J].Journal of Algebra,2010,324: 652-672.
[8]SHU B,ZHANG C W.Representations of the restricted Cartan type Lie superalgebra W(m,n,1)[J].Algebras and Representation Theory,2011,14:463-481.
[9]SHU B,YAO Y F.Character formulas for restricted simple modules of the special superalgebras[J].Mathematische Nachrichten,2012,285:1107-1116.
[10]YAO Y F.On restricted representations of the extended special type Lie superalgebra[J].Monatshefte für Mathematik,2013,170:239-255.
[11]YAO Y F.Non-restricted representations of simple Lie superalgebras of special type and Hamiltonian type[J]. Science China Mathematics,2013,56:239-252.
[12]YAO Y F,SHU B.Restricted representations of Lie superalgebras of Hamiltonian type[J].Algebras and Representation Theory,2013,16:615-632.
[13]YAO Y F,SHU B.A note on restricted representations of the Witt superalgebras[J].Chinese Annals of Mathematics,Series B,2013,34:921-926.
[14]YUAN J X,LIU W D.Restricted Kac modules of Hamiltonian Lie superalgebras of odd type[J].Monatshefte für Mathematik,2015,178:473-488.
[15]WANG S J,LIU W D.On restricted representations of restricted contact Lie superalgebras of odd type[J]. Journal of Algebra and Its Applications,2016,15(4):1650075,14pages.
[16]JANTZEN J C.Representations of Lie algebras in prime characteristic[C]//Proceedings of the NATO ASI Representation Theories and Algebraic Geometry.Montreal,1997,514:185-235.
[17]STRADE H,FARNSTEINER R.Modular Lie Algebras and Their Representations[M].New York:Marcel Dekker,1988.
[18]HUMPHREYS J E.Introduction to Lie Algebras and Representation Theory[M].New York:Springer,1972.
[19]JACOBSON N.Lie Algebras[M].New York:Interscience,1962.
[20]PETROGRADSKI V.Identities in the enveloping algebras for modular Lie superalgebras[J].Journal of Algebra, 1992,145:1-21.
(责任编辑:林磊)
有限维李超代数的模表示
杨恒云,姚裕丰
(上海海事大学数学系,上海201306)
研究了特征大于2的代数闭域上有限维李超代数的表示.证明了有限维李超代数的单模都是有限维的,并且所有单模的维数有上界.进一步,一个有限维李超代数可以嵌入到一个有限维限制李超代数.给出了有限维限制李超代数g上单模的判定准则,定义了g的一个限制李超子代数,得到了该子代数的单模同构类和g的单模同构类之间的一个双射.这些结果是素特征域上李代数相关理论的推广.
李超代数;表示;p-包络;p-特征
2017-03-01
国家自然科学基金(11571008,11671138);上海市自然科学基金(16ZR1415000)
杨恒云,女,副教授,研究方向为李理论及表示理论.E-mail:hyyang@shmtu.edu.cn.
姚裕丰,男,副教授,研究方向为李理论及表示理论.E-mail:yfyao@shmtu.edu.cn.
O152.5Documentcode:A
10.3969/j.issn.1000-5641.2017.03.001
1000-5641(2017)03-0001-19

