转轴扭转变形动态测量噪声消除方法研究

尹学峰 朱玥琦 吉小军

(上海交通大学电子信息与电气工程学院，上海 200240)

转轴扭转变形动态测量噪声消除方法研究

尹学峰 朱玥琦 吉小军

(上海交通大学电子信息与电气工程学院，上海 200240)

转轴的扭转变形信号中包含了大量与转轴运行状态相关的信息，但往往被噪声所淹没，合理的去噪处理能够得到更有效的信号成分，有助于对转轴的工作状态做出正确的判断。相比于传统滤波方法，基于EMD的去噪方法有较强的自适应性，更适合动态信号的处理。从转轴相互正交的两个方向采集的相位差信号，依据两路信号EMD分解后各阶本征模态函数的相关性去除噪声并恢复出有效信号。仿真验证了该方法的有效性，并将其运用到实际转轴扭转变形信号的处理中，得到了更为准确的扭转变形信息。

转轴 扭转变形 测量 相位差 EMD 去噪

1 引 言

转轴扭转变形是由大小相等，方向相反，作用面都垂直于杆轴的两个力偶引起的，表现为杆件的任意两个横截面发生绕轴线的相对运动。轴扭转变形能够反映出轴的负载特性、安全性以及材料特性等许多信息，在机械工程领域这是一项基础而关键的测试需求，特别是转轴的动态扭转变形能够间接表征旋转机械的扭矩、功率等运行状况信息，从而可以对设备的动力特性、运行可靠性进行检测和故障诊断。因此，轴扭转变形测试是机械产品开发、质量检测、优化控制、工矿检测和故障诊断的重要内容。

关于转轴动态扭转变形的测试，国内外有关机构已经进行了大量的研究和开发工作[1]，其中主要的技术手段是采用编码器来测量轴扭转角的方法，将两个编码器沿轴向一定间隔安装在转轴上，测量由编码器发出的脉冲时间间隔可以获得轴在安装编码器的断面处的角速度，通过比较转轴二端断面的角速度，进而得到扭转角速度和其他有关扭角、扭振的信息。清华大学张晓玲提出了一种扭转变形测试的技术方案[2]，但是并没有涉及因轴系旋转而引起的动态振动噪声的处理问题。太原理工大学孙良环提出了应用高精度光电编码器测取扭振信号，用希尔伯特变换法进行扭振信号分析，并尝试了利用该扭振测量方法对齿轮进行故障诊断的研究[3]。但该文献侧重对扭振信号的测试和分析，没有涉及扭转变形与振动信号的分离问题。

针对转轴扭转动态扭转变形的测量问题，在前期对测试方法和系统设计与实现进行研究的基础上[4]，本文着重研究动态测试信号的处理问题，提出了采用EMD方法来消除由于转速波动和轴系振动等对测试结果的影响，对实现的基本原理和具体过程进行了详细说明，对其有效性进行了理论仿真和实验测试。

2 转轴动态扭转变形测试方法及其振动影响分析

弹性轴在受到大小为N的扭矩载荷作用时，轴将产生扭转形变，相距长度为L的截面绕中心轴发生相对转动，从而产生一个扭转角θ

(1)

式中：G——材料的剪切弹性模量；IP——横截面对圆心的极惯性矩。因此转角θ就代表了轴的扭转变形量，也反映了轴的机械特性，在预先测得轴的剪切弹性模量和极惯性矩的情况下，便可由转角θ计算出轴承受的扭矩载荷值。

在前期的研究中，我们已开发了如图1所示的轴扭转变形动态测量系统[4]，通过在被测旋转轴相隔一定距离的位置处平行地加工上反光/不反光的色标带，在与被测轴通过轴承相固连的套筒A、B位置安装两个反射式激光测头。为了抑制振动影响，在与A/B正交的位置C/D也布置一组同样的探头，测试中可以同步得到两组信号(在下文中A/B、C/D产生的信号分别记为x路、y路信号)。

当转轴旋转并承受一定的扭矩载荷时，A、B两位置处传感器会输出频率相同但存在固定相位差的两路脉冲信号，如图2所示。脉冲信号周期T反映了轴的转速，两路脉冲的相位差T1变化反映了转轴发生的扭转变形角，色标带的数目决定了测量的动态特性。假设色标条数目为m，则脉冲信号的周期T和转速n(r/min)的关系为

(2)

扭转角θ和相位差T1的关系为

(3)

由式(1)～式(3)可以看出，只要测出脉冲信号的周期T和两路脉冲信号的相位差脉宽T1，就可以得知一定扭矩载荷下扭转角的大小。测试系统中采用了FPGA高速计数器来对周期和脉宽进行填充计数测量，由于周期T的值会因为转速的不同而变化，每个脉冲周期会同时测量一个相位差计数值T1，这样的测量过程从空间上看是对转轴等角度间隔(即Δθ=360/m)进行取样。从时间上看，数据采集可以理解为按照可变的采样间隔T对相位差信号采样，即一个变采样率的取样过程，实际采样率是与转速密切相关的。

另一方面，由于一般转轴的剪切弹性模量都很大，由扭矩载荷引起的扭转变形量非常小，在测量过程中，转速的波动及其机械系统的振动等会引起脉冲波前后沿的非同步抖动，这样会造成测量的信噪比非常低，从而会给转速和相位的测量带来很大的影响。实际测试中转速波动和机械振动是被测对象自身存在的难以消除的因素，因此为了准确的进行微弱的扭转变形量测量，必须采取合适的信号处理方法对振动噪声进行分离和消除。

3 基于EMD的振动噪声分离与处理

3.1 EMD分解

从相关文献来看，目前对动态振动信号处理中采用的方法主要有自适应滤波、小波分解以及神经网络等。这些常用的方法都需要对被处理对象有一定的先验知识，如应用最多的小波方法，其处理效果在很大程度上取决于小波基函数的选择，在实际工程应用中，恰当的小波基函数选择困难且不具备自适应性。经验模态分解法(Empirical Mode Decomposition, EMD)是新发展起来的处理非线性非平稳信号的时频分析方法。这种方法吸取了小波变换多分辨率的优点，同时又克服了小波方法中基函数选择困难且不具备自适应性的缺陷[5]，因而可以较好地用来对非平稳信号进行滤波和去噪。该方法的主要思想是把一个时间序列的信号分解成若干不同尺度的本征模态函数(Intrinsic Mode Function, IMF)和一个残余量。各IMF反映了信号的局部特性，残余量反映了信号的趋势或均值。各IMF要满足两个条件[6]：①整个信号中零点数与极点数(包括极大值点和极小值点)相等,最多相差1；②信号上任意一点，由局部极大值点确定的包络线和由局部极小值点确定的包络线均值均为零[7]，即信号关于时间轴局部对称，具体分解过程可采用以下方法：

(1)首先确定出信号x(t)的所有极大值点和极小值点，然后将所有极大值点和极小值点分别用三次样条曲线拟合，从而获得信号的上包络曲线和下包络曲线，计算出它们的平均值曲线m1(t)，用x(t)减去m1(t)得

h1(t)=x(t)-m1(t)

(4)

(2)若h1(t)不满足IMF的两个条件，则将h1(t)作为原信号重复第(1)步，直到满足条件，完成IMF第一阶分解得

C1(t)=h1k(t)

(5)

(3)从原信号中减去C1(t)，得第一阶剩余信号

r1(t)=x(t)-C1(t)

(6)

再把r1(t)作为新的原信号，重复第(1)、(2)步，依次得到C2(t)、r2(t)、C3(t)、r3(t)、…Cn(t)、rn(t)。

(4)当rn(t)成为一个单调函数时，筛分结束。由此得到把原始数据表示为本征模态函数分量和一个残余项之和。这样原始信号便分解为

(7)

从上述的EMD分解过程可以看出，这种分解方法可以理解为以信号的极值特征尺度为度量的筛分过程。信号从最小的特征尺度进行筛分，从而获得最短周期的固有模态函数，随后，经过一层层的筛分,获得周期长度逐渐增大的多IMF，这个过程也体现了多分辨分析的滤波过程。越早分解出来的本征模函数频率越高，第一个分解出来的代表原信号的最高频率成份。这种滤波器充分保留了信号本身的非线性和非平稳特征，具有自适应强，对信号类型没有限制的特点。利用这些特征可以有效的去除信号的噪声干扰，充分保留信号的局部特征，在动态变采样率信号的滤波和去噪中具有很大的优势。

在实际测试中，振动噪声信号频率相对较高，对应与较低阶的IMF，被测扭转变形一般为静态和准静态，信号频率性对较低，对应与较高阶的IMF。按照上面EMD分解方法，分别对x、y二路相位信号做处理，得到如下二个分解

(8)

(9)

为了便于程序处理，把上式中的残余项和各阶IMF统一到一起，可以表示如下(最后一项即为残余项)

(10)

(11)

3.2 相关性处理

由于在轴上正交位置测量得到的振动噪声信号具有一定的随机性，两组信号的相关性较低。而被测的扭转变形信号是由相同的载荷作用引起的，理论上在正交位置处也完全相同，且采用了同步采集，所以理论上两路信号具有很强的相关性。因此通过对两路信号各阶本征模态函(IMF)作相关分析，提取相关系数大于设定阈值的本征模态函数(IMF)作为有效信号，然后对两组有效信号做加权平均来得到被测信息即轴扭转变形的测试结果，理论上可以实现自适应动态噪声分离和抑制。

以第i阶为例,x、y路信号的第i阶IMF分别为imfx(i)，imfy(i)，这里的i表示第i阶而非表示序列内的序列标号。假设每个IMF内有n个点，不妨把两个IMF分别写作imfx(n)，imfy(n)。然后做互相关

(12)

归一化互相关计算结果，使相关性系数处于[-1,1]区间内。相关性系数各子区间对应的相关程度如下表所示。

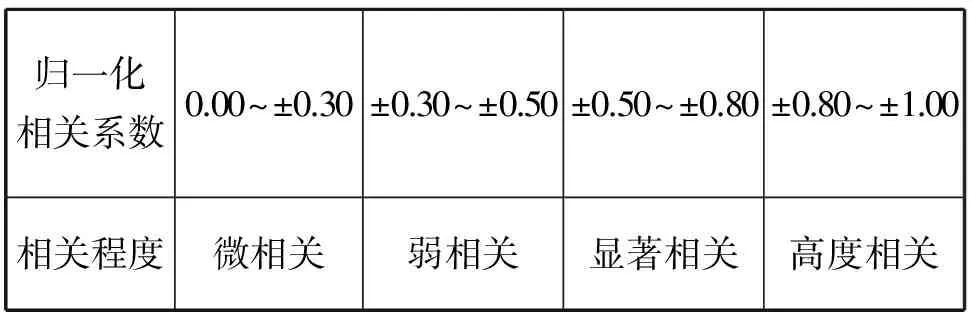
表1 相关性系数各子区间对应的相关程度

建立一个与IMF最大阶次相同的用以表征对应阶的IMF是否有效的哈希表hash(i)，初始值全部为0，当第i阶的x、y路信号的IMF相关系数大于设定的阈值时，有

hash(i)=Rxy(m)

(13)

把有效IMF依据其对应的相关系数加权合成(hash(i)即为权重)

(14)

由于二路信号的IMF最大阶次可能不同，所以必然会存在舍弃低阶或者高阶IMF的情况，因此在做互相关时，先从低阶到高阶做互相关分析，再从高阶到低阶做一次，记录下二次相应的hash(i)，取hash(i)中值最大的求互相关方向作为最终互相关分析以及后续IMF合成的方向。

4 仿真与实验测试

4.1 仿真实验

为了验证本文所提出的基于EMD的动态噪声处理方法的效果，本节首先结合被测对象特点，构建仿真模型，通过理论仿真验证。以转速1 000r/min，转速随机波动10%，对转轴分别施加1Hz正弦扭矩和线性增加扭矩，附加30%随机噪声为仿真例，如图3所示为EMD分解过程及其处理前后的比对。由仿真结果可以看出，应用本文所提出的EMD去噪方法对正弦、线性增加三种动态仿真信号做去噪处理，可以达到非常理想的效果。

4.2 实际测试

以前期构建的动态扭矩试验台为测试对象，通过实际测试和数据处理，比对验证本文所提出的EMD方法的对实际测试系统的有效性。考虑到激光-反射栅相位差测试系统在安装好后会存在初始零位误差，首先在转速为100r/min、外加扭矩为0条件下进行试验获取初始零点，然后分别在转速为50r/min，100r/min，150r/min，200r/min，扭矩载荷设定为500N·m的条件下进行试验测试和处理，结果如图5所示。

上面四幅图中每幅图的(a)表示每二个脉冲记录点之间的时间间隔随时间的变化情况；图(b)表示转速，图(c)中虚线、点划线分别为原始的x、y路相位差信号，实线为经过EMD去噪后的信号。

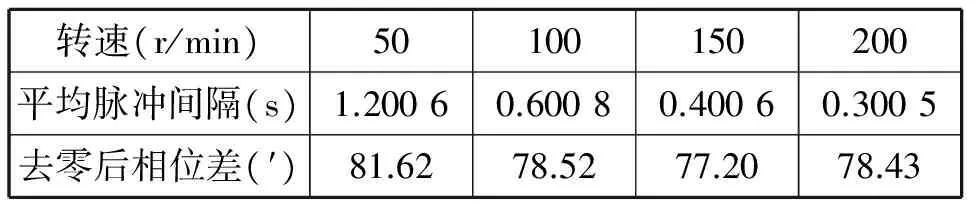
表2 对实测信号的处理结果

5 结束语

经验模态分解分析方法，能够自适应地将信号分解成不同频段的本征模态函数，并可通过有选择地组合实现噪声分离与信号提取。本文通过引入正交的两组同步信号的相关分析进一步实现了信号增强和噪声抑制，较好地实现了振动环境下对实测的磁信号的处理表明，这种方法可以有效地抑制噪声从而提取出清晰的缺陷信号,达到与小波变换几乎一致的处理结果。与小波变换相比，本征模态函数直接由原始信号分离得到，算法简单快捷，物理意义明显，且不受傅里叶变换及测不准原理的限制。同时，由于这种方法不是基于波形匹配原则，因此分解效果不受小波函数选择的影响，研究结果对管道缺陷检测中漏磁信号的处理提供了一种新的技术途径。

[1] 段国芳，苗岩松. 国内扭矩测试方法综述[J]. 测试技术学报， 1997， 11(4)： 44～47.

[2] 张晓玲，唐锡宽. 转轴扭角及扭振测试技术研究[J]. 清华大学学报，1997， 37(8)：83～86.

[3] 孙良环. 基于希尔伯特变换的扭振测量方法及其在齿轮故障诊断中的应用[D]. 山西: 太原理工大学.

[4] 丁珍红. 一种轴扭转变形动态测量系统的设计及实现[J]. 中国机械工程，2011， 22(14)： 1 672～1 675.

[5] Huang N Shen Z， Long R，et al. The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Procroy.soc Lond. a, 1998， 454(1971)：903.

[6] 万鹏. 基于流形学习的主轴系统故障诊断方法研究[D]. 北京信息科技大学， 2013.

[7] 胡劲松. 面向旋转机械故障诊断的经验模态分解时频分析方法及实验研究[D]. 浙江大学， 2003.

Reduction of Dynamic Noise in the Measurement of ShaftTorsional Deformation Based on EMD

YIN Xue-feng ZHU Yue-qi JI Xiao-jun

(School of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

A large number of information related to the running state of the rotating shaft is contained in the torsional deformation signal of the shaft. Reasonable method can get more effective signal components, it can help to make correct judgement on the working state of the shaft. Compared with the traditional denoising method, the method based on EMD has a strong adaptability. Effective signal is recovered from the original signals collected from two mutually orthogonal directions, after being filtered outnoise according to the correlation of EMD decomposition. The simulation results show that the method is effective and can be used to the actual rotating shaft to reduce the distortion of the signal.

Shaft Torsional deformation Measurement Phase difference EMD Noise reduction

2016-05-24

尹学峰(1990-)，男，硕士研究生，主要研究方向：测试、计量和信号处理。

1000-7202(2017) 02-0043-06

10.12060/j.issn.1000-7202.2017.02.09

TP391

A