基于导纳测量原理的隐极发电机失磁保护应用
兀鹏越,徐雷钧,王正元,王智高
(1.西安热工研究院有限公司,陕西 西安 710032;2.江苏大学 电气信息工程学院,江苏 镇江 212013;3.华能天津煤气化发电有限公司,天津 300452)
0 引言
发电机失磁保护是发电机的主保护之一,常见的失磁保护判据分为定子侧判据和转子侧判据,一般以定子侧判据作为主要判据。我国传统的发电机失磁保护采用阻抗原理,而目前实际工程中,国产和大部分国外的发电机保护装置的失磁保护定子侧判据都是基于阻抗平面的,由静态稳定阻抗圆和异步阻抗圆组成的失磁保护得到了广泛应用。
导纳和阻抗是倒数关系,因此基于阻抗平面的失磁过程也可以在导纳平面进行描述,这在有关著作中是有论述的[1]。由于导纳平面和发电机功率平面(以下简称P-Q平面)有天然的相似性,在导纳平面上的失磁保护特性可直观地满足励磁限制与失磁保护的配合关系,从而避免了目前工程上的失磁保护阻抗圆与励磁限制曲线配合计算难题,因此基于导纳原理的失磁保护在工程上具有一定的优越性。
西门子公司的发电机失磁保护装置采用了与众不同的导纳测量原理。由于该原理保护在国内应用较少,在DL/T 684—1999《大型发电机变压器继电保护整定计算导则》[2](下文中简称《导则》)没有提及,因此国内工程技术人员对此还不熟悉。目前,该保护的相关资料也比较缺乏,除了厂家说明书①Multifunction generator,motorand transformerprotection relay 7UM62.Siemens Manual,2001.的一般性介绍外,仅有少量文献[3-4]提到了基于导纳测量原理的失磁保护实际应用。而且这些文献都是基于厂家说明书的简单论述,既没有透彻地揭示常规阻抗原理与导纳原理在本质上的一致性,使得技术人员未能深入理解导纳特性,常常误认为是完全不同的失磁保护原理;也未能指出厂家整定原则与国内常规整定计算的不同之处,不能灵活地将《导则》的整定思想准确地应用到基于导纳测量原理的失磁保护整定计算中,给基于导纳测量原理的失磁保护在国内的应用造成一定障碍。因此,有必要对基于导纳原理的失磁保护在工程上的应用进行研究。
1 基于阻抗平面的失磁保护
在传统继电保护中,发电机进相运行程度是通过发电机机端阻抗测量值来反映的。失磁阻抗是基于发电机额定电压和额定视在功率下,根据发电机暂态电抗 x′d、同步电抗 xd、系统电抗 xs,形成静态稳定圆与异步圆的阻抗轨迹,见图1。图中,Xa、Xb、Xc为发电机失磁保护阻抗轨迹与X轴的交点。
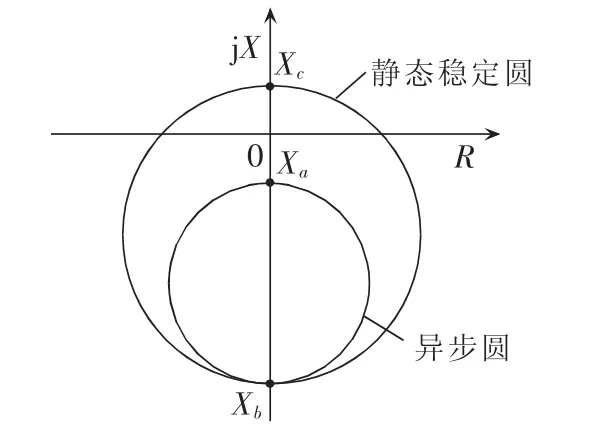
图1 失磁保护阻抗特性圆Fig.1 Impedance circle of under-excitation protection
设失磁保护阻抗圆的圆心为(0,x0)、半径为R0,其方程为:
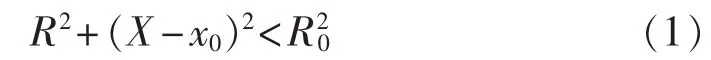
根据《导则》中失磁保护阻抗圆的整定规定,取Xa=x′d、Xb=xd、Xc=xs,则在阻抗平面上的静态稳定圆方程为:
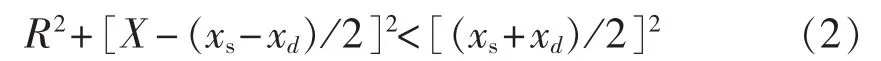
阻抗平面上的异步圆为:
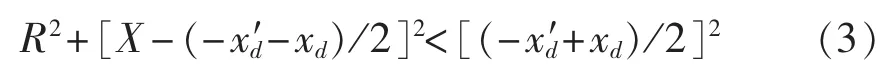
当发电机失磁时,机端测量阻抗由第一象限进入第四象限,当阻抗落入外圆内部时表示失去静态稳定,继续进入内圆则表示发电机异步运行,由此判断出发电机失磁。
失磁保护的阻抗原理长期以来得到广泛应用,但存在失磁保护与励磁限制配合困难的问题。按照规程要求,为了防止励磁限制与继电保护定值失配,必须要校核励磁系统低励磁限制与失磁保护的整定配合,以及失磁保护与进相运行极限的配合关系。正确的配合关系是要求发电机进相时,首先达到的是最大进相深度限制曲线,其次是励磁限制曲线,最后是失磁保护曲线。为了比较这三者关系,需要将三者映射在同一个坐标系。可以将失磁保护的阻抗特性映射到发电机P-Q平面进行比较,也可将发电机P-Q平面上的低励限制曲线映射到阻抗RX平面[5]。这2种方法都可行,但显然都建立在繁复的数学计算基础上,具有一定的难度。
2 基于导纳平面的失磁保护
将发电机机端导纳特性作为失磁保护的主要判定方式,最早是由德国西门子公司提出的[3]。其原理是,根据在标幺制下发电机导纳特性与发电机运行极限特性相同的特点,在P-Q平面表示的发电机运行极限特性曲线上,直接给出表示静态稳定特性和动态稳定特性的曲线,作为失磁保护的动作边界。保护装置测量发电机的导纳,当导纳超出特性曲线时,即判断发电机失磁。
2.1 导纳特性与发电机极限特性的转换关系
复功率为:
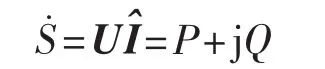
导纳的定义为:
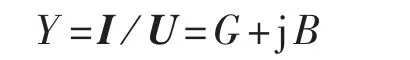
也即:
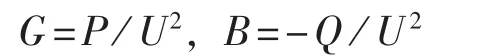
根据以上转化公式,可将发电机运行极限特性曲线以标幺值的标定方式转换成导纳平面图。在标幺制下,发电机导纳特性与发电机运行极限特性是相同的,区别只在于在无功方向反向180°,见图2。图中,横轴、纵轴各量均为标幺值。
保护装置通过瞬时值采样得到发电机三相电压、电流的矢量,然后通过这些矢量数据计算出电压、电流的正序分量,再计算出发电机有功功率和无功功率,按照复功率公式除以正序电压的平方,就将功率平面转换到了导纳平面。
2.2 基于导纳测量原理的失磁保护判据
西门子的发电机失磁保护是在导纳平面上,整定出3个相互独立的特性段即特性1、特性2、特性3,用这3段特性曲线来表示同步发电机的静态稳定极限边界与动态稳定极限边界,见图3。
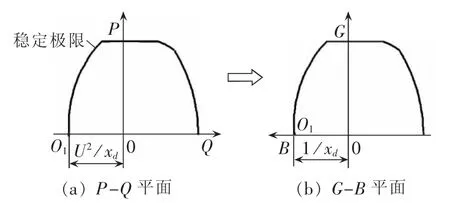
图2 发电机运行极限映射到G-B平面上Fig.2 Mapping of generator operational limit curve on G-B plane
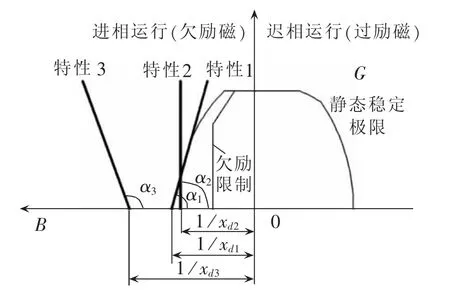
图3 基于导纳特性的失磁保护特性曲线Fig.3 Characteristic curves of under-excitation protection based on admittance measurements
(1)静态稳定极限边界——特性1、特性2。
当发电机发生欠磁后,由于发电机的感应电动势E0随着励磁电流的减小而减小,电磁转矩也将小于原动机的转矩,因而引起转子加速的趋势,使发电机的功角δ增大,发电机由发出无功功率转为吸收无功功率,开始进入进相运行。随着进相的深入,发电机的运行限额可能超出了静态稳定的边界。当发电机超过静态稳定的边界以后,就表明发电机已经超过静态稳定极限,失去同步。
在西门子的发电机失磁保护中,用特性1和2模拟静态稳定极限边界,等效于阻抗平面上的静态稳定阻抗圆。图3中,静态稳定边界是一段圆弧,西门子的发电机失磁保护中用特性1、2来模拟。
(2)动态稳定极限边界——特性3。
按照西门子提供的说明书,特性3是发电机的动态稳定极限曲线。当导纳的测量值越过本特性曲线时,发电机必将失去稳定,跳闸命令立即发出。特性3模拟动态稳定极限边界,其整定值一般是根据经验值得到,说明书特别要求该值要大于1。
(3)失磁保护的逻辑。
上述3条特性曲线和转子侧的励磁低电压判据共同组成了完整的失磁保护逻辑,见图4。
特性1、特性2经长延时跳闸,这是因为此时随着励磁调节器的作用,有可能再次将机组拉回静态稳定极限以内。如果此时发电机低电压判据(U1<)及励磁电压故障判据(>Uexe.fail)满足,则短延时跳闸。
特性3已超过动态稳定极限曲线,发电机肯定失去稳定,立即跳闸。
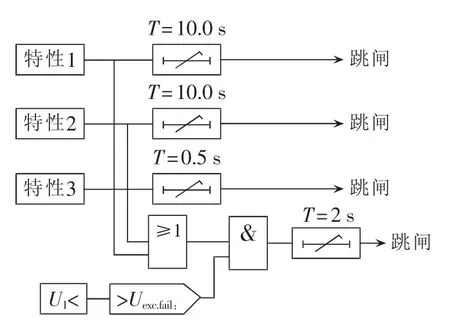
图4 失磁保护逻辑图Fig.4 Logic diagram of under-excitation protection
2.3 基于导纳测量原理的失磁保护优点
基于导纳测量原理的失磁保护直观易懂、易于整定。从图2中可见,在无功方向将相角反向转动180°后,可将发电机的运行极限图变换到导纳特性平面中,图形完全相同。因此将导纳特性判据与发电机的运行极限特性曲线进行比较,显然更加直观、简便。基于导纳测量原理的失磁保护的整定是不需要计算的,可以直观地从发电机P-Q曲线上获得。
基于导纳测量原理的失磁保护的另一个优点是易于与励磁限制配合。由于目前大部分励磁调节器采用的低励限制曲线都是P-Q平面的曲线,因此,基于导纳测量原理的失磁保护特性曲线、发电机运行极限曲线、低励限制曲线将可在同一平面通过目视直观绘制得出,无需任何计算,解决了长期困扰技术人员的失磁保护与励磁限制配合整定计算问题。
3 2种失磁保护原理的比较分析
3.1 阻抗特性和导纳特性的映射关系
由复功率定义可知:
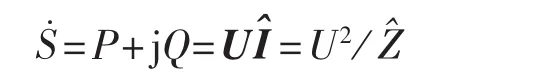
则有:
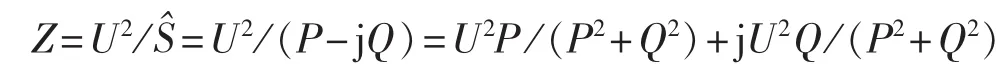
令 R=U2P/(P2+Q2)、X=U2Q /(P2+Q2),将 R 和X的表达式代入式(1),得:
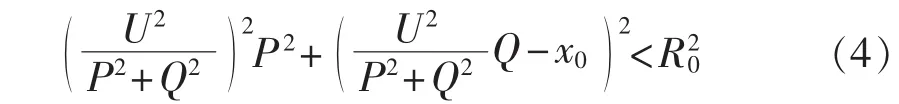
对于静态稳定阻抗圆,,化简式(4)得:
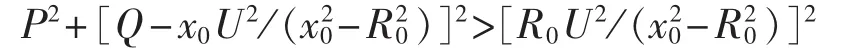
可见,静态稳定阻抗圆在P-Q平面上的映射是一个圆,圆外为动作区。由于,映射圆的圆心在Q轴正半轴上。根据《导则》整定要求,在图1 中取 Xb=xd、Xa=xs,即 x0=(xs-xd) /2、R0=(xs+xd)/2,可得到P-Q平面上发电机静态稳定极限圆:
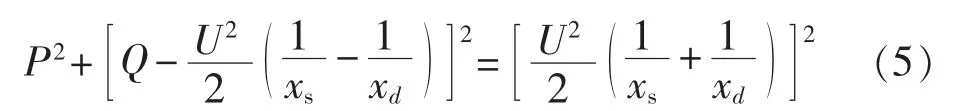
对于异步圆,,化简式(4)得:
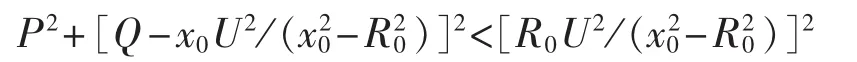
可见,异步阻抗圆在P-Q平面上的映射也是一个圆,圆内为动作区。由于,映射圆的圆心在Q轴负半轴上。
根据《导则》整定要求,在图1 中取 Xa=x′d、Xb=xd,也即 x0=(-x′d-xd) /2、R0=(-x′d+xd) /2,即可得到P-Q平面上发电机异步圆为:
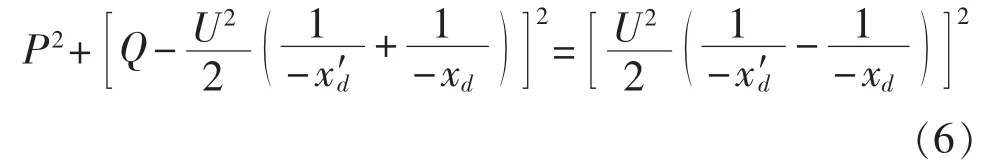
图5给出了图1中静态稳定圆和异步圆在阻抗平面和导纳平面的映射关系。阻抗平面内的静态稳定圆Z1和异步圆Z2分别映射为P-Q平面内的静态稳定圆 z1和异步圆 z2,点 A、B、C 分别映射为a、b、c。注意,在阻抗平面中Z1、Z2内部是动作区,而映射到P-Q平面后圆z1外部是动作区、圆z2内部是动作区。
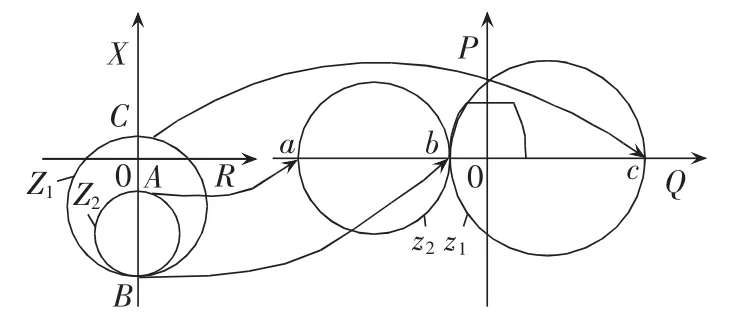
图5 静态稳定圆和异步圆在阻抗平面和导纳平面上的映射关系Fig.5 Mapping relationship of steady-state circle and asynchronous circle between impedance plane and admittance plane
可见,静态稳定圆和异步圆的导纳特性和阻抗特性是完全可以对应起来的,本质上具有一致性,也即西门子的发电机失磁保护与国内常用的阻抗原理失磁保护本质也是相同的(西门子的发电机失磁保护动作特性1、2、3是关于Q轴对称的,其动作区包含Q轴以下部分,本文各图中未画出)。
3.2 西门子失磁保护整定问题分析
西门子给出的失磁保护整定方法见于装置说明书和有关文献[3]介绍。其中用特性1和特性2模拟静态稳定圆,即图5中圆z1在P-Q平面第二象限的圆弧,这一点比较直观,国内技术人员容易理解。但是国内技术人员对于特性3所反映的“动态稳定边界”的含义就不是很清楚。装置说明书指出该定值是横坐标轴与特性3的交点,根据经验给出,且要求该值要大于1,但并未给出理由,这是现场定值整定时一个困惑的地方,其他文献均没有对此给予明确说明。
经咨询西门子技术人员得知,特性3实际上是模拟导纳平面上的圆弧,所谓动态稳定边界即稳定异步运行边界,也即是国内所表示的阻抗平面内的异步圆。《导则》规定异步阻抗圆是与静态稳定阻抗圆相切于-Xd(Xd为同步电抗)的,也即图6中的异步圆1;而根据西门子特性3整定结果(必须大于1)对应的异步阻抗圆和静态稳定阻抗圆是不会相切的,也即图6中的异步圆2,这是两者的区别所在。
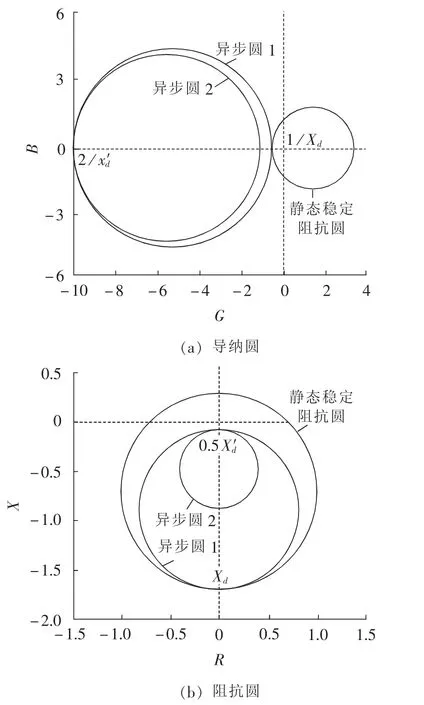
图6 仿真分析Fig.6 Simulative analysis
由图6中阻抗圆和导纳圆的定量仿真结果可以看出,当导纳平面异步圆与静态稳定圆外切于1/Xd时,对应的阻抗平面中异步圆与静态稳定圆内切于Xd。随着导纳平面中的异步圆向左移,阻抗平面中异步圆向上移,不再与静态稳定圆相切,且圆面积迅速变小。但是由于发电机失磁后最终都会进入稳定异步运行,均会进入这2个动作区,都会动作,但进入异步圆1的动作时间快于异步圆2。
按照我国《导则》规定的异步圆为异步圆1,对应的特性3位置应该是与特性1相交于横轴的1/Xd处。即如果按照《导则》的思想来整定特性3,应该是小于1的。
4 基于导纳测量原理的失磁保护整定算例
以华能IGCC电站180 MW发电机所配置的西门子7UM62保护装置为例,对基于导纳测量原理的失磁保护进行定值整定。机组的主要参数见表1。
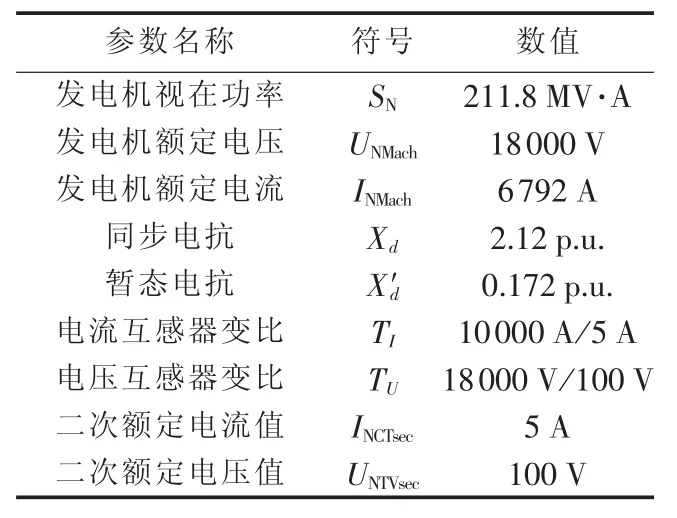
表1 机组参数Table 1 Parameters of generator
导纳特性曲线的整定有2种方法。一种是直接测量法,在发电机运行极限特性曲线上通过测量直接获得特性1、2、3的有名值,然后将有名值转换为标幺值即为最终的整定值。另一种是计算法,只需要知道发电机同步电抗,即可算出特性1、2、3。
4.1 直接测量法
a.测量特性曲线。
直接测量法是在发电机极限运行图上直接绘制出与发电机限额特性曲线的静态稳定极限边界相切的失磁保护的特性1和特性2,然后测量2条特性与Q轴的交点处的无功功率以及特性1的角度。表1机组的发电机极限运行曲线如图7所示,图中曲线 1、2、3 分别为测量法的特性 1、2、3,曲线 4、5、6 分别为计算法的特性 4、5、6。实测可知:特性 1,Q1≈148.0 Mvar,α1=74°;特性 2,Q2≈102.0 Mvar,α2=90°;特性 3,Q3≈102.0 Mvar,α3=110°。
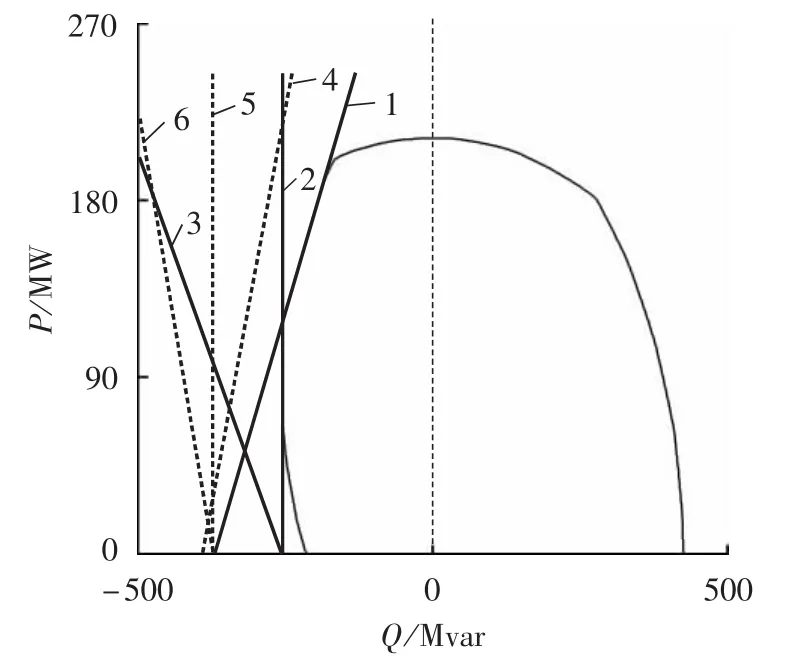
图7 测量法与计算法得到的失磁保护特性值的比较Fig.7 Comparison of under-excitation protection characteristic curves between measurement method and calculation method
b.标幺值归算。
保护装置中的定值为标幺值,为此,需要将测量到的Q1、Q2有名值归算为标幺值。归算过程如下:
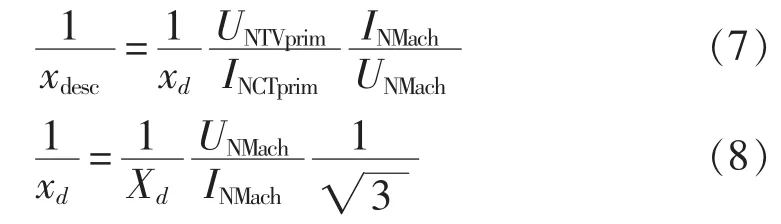
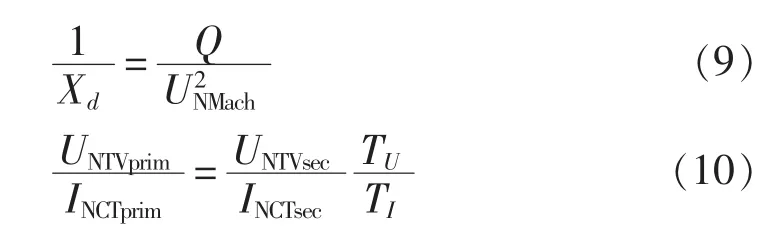
其中,xdesc为同步电机的直轴同步电抗二次标幺值;UNTVprim为电压互感器的一次侧额定电压;INCTprim为电流互感器的一次侧额定电流。
将式(7)—(10)合并可得:

将测量值 Q1、Q2代入式(11)中,得到特性 1、2分别如式(12)、(13)所示。

如3.2节所述,特性3取值与特性2相同,仅角度不一样。
将励磁调节器的低励限制曲线绘制在同一张图中,可以直观地看到这两者的配合关系,见图7。
4.2 计算法
计算法是由发电机同步电抗来计算出特性1、2、3的Q值,而特性曲线的角度则在一定范围内根据经验给出。
本例中发电机同步电抗xd=2.12 p.u.,将其取为特性2和特性3的定值,特性角度根据经验选择。
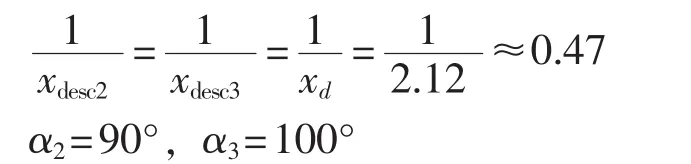
特性1的定值将特性2左移得到,可以乘以一个系数,如1.05,角度可选择为80°,则特性1为:
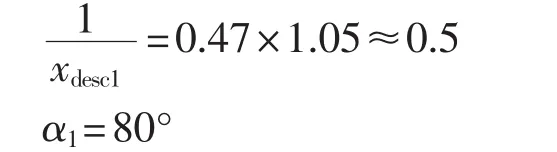
将计算法获得的特性表示在发电机运行极限图上,依据以下公式计算出对应的无功功率:
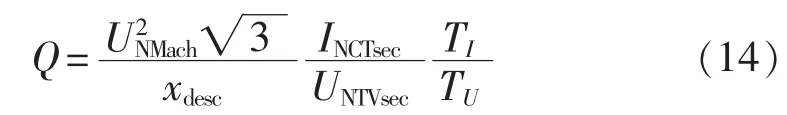
可得:
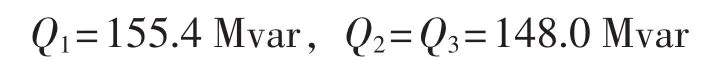
将归算后的特性1、2、3绘制在发电机运行特性图上,可以与低励限制等曲线进行比较,以确定它们的配合关系是否合理。
4.3 2种方法的比较
直接测量法是依据制造商提供的发电机运行极限曲线绘制的,具有简单、直观的优点。
计算法整定导纳特性与《导则》思想是一致的。《导则》中对失磁保护的阻抗圆整定主要依靠发电机电抗值来进行,而不考虑发电机运行极限曲线。
将这两者所得结果都画到发电机运行极限曲线上可以看出,这2种整定方法获得的保护范围是不完全一致的,原因在于发电机运行极限曲线与同步电抗的不同,但2种方法所得定值都满足与低励限制的配合关系。
5 进相试验对失磁保护的验证
图7中在P-Q坐标上绘出发电机运行限制曲线(制造厂给出)、低励限制曲线、失磁保护特性曲线,以及进相试验过程的运动轨迹。可以看出,基于导纳测量原理的失磁保护和低励限制曲线可以直观比较,配合关系清晰,物理意义明确。
发电机进相试验目的是实际测试发电机进相运行的最大深度,通过该试验还可以实际验证发电机失磁保护和低励限制的配合关系。正确的配合关系应当是发电机进相深度逐渐加深时,首先达到的是进相限制曲线,继续加深进相运行达到的是励磁限制曲线,再继续进相才会导致失磁保护动作。
表2是华能IGCC电站180 MW发电机进相试验时,不同负荷下达到最大进相深度的试验数据,试验过程失磁保护不退出,失磁保护定值采用测量法整定。由表2可知,在负荷119.9 MW进相时,无功功率为-80.9 Mvar,此时励磁调机器低励限制动作,达到发电机进相运行的最大深度,而失磁保护无异常,证明失磁保护和励磁限制器配合关系正确。
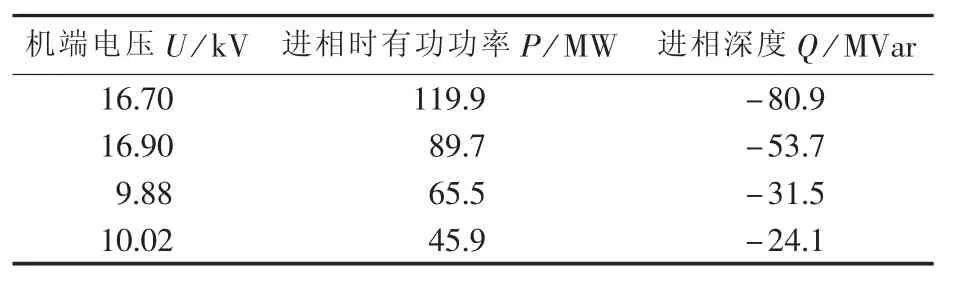
表2 进相试验数据Table 2 Data of leading-phase experiment
6 结语
采用导纳测量原理的发电机失磁保护与采用阻抗原理的失磁保护在本质上是一致的。但比较而言,采用导纳测量方法构成的失磁保护具有物理意义清晰、直观、易于整定、易于与励磁限制特性配合的优点。
虽然西门子的发电机失磁保护中的动态稳定特性等同于国内异步运行特性,但整定原则不同。按照《导则》思想也可整定导纳测量原理的失磁保护,且比西门子整定原则更合理,基于导纳测量原理的失磁保护也应按照我国标准整定。
参考文献:
[1]王维俭,候炳蕴.大机组继电保护理论基础[M].北京:水利电力出版社,1989:366-386.
[2]国家能源局.大型发电机变压器继电保护整定计算导则:DL/T 684—2012[S].北京:中国电力出版社,2012.
[3]Dr.Hans Joachim Herrmann,高迪军.基于导纳测量方法的发电机失磁保护-极为贴近发电机的运行极限图[C]∥中国水利发电工程学会继电保护专业委员会2009年年会.北京:中国水利发电工程学会继电保护专业委员会,2009:596-605.
[4]安亮.基于导纳测量原理的发电机失磁保护定值整定[J].河北电力技术,2013,32(4):44-46.AN Liang.Loss-of-excitation protection value setting based on admittance measurement principle[J].Hebei Electric Power,2013,32(4):44-46.
[5]王维俭,桂林,王雷,等.发电机失磁保护定值整定的讨论——对2007 年版《IEEE Guide for AC Generator Protection》的斟酌[J].电力自动化设备,2009,29(3):1-3.WANG Weijian,GUI Lin,WANG Lei,et al.Discussion on setting calculation of generator loss-of-excitation protection:thinking of IEEE Guide for AC Generator Protection published in 2007[J].Electric Power Automation Equipment,2009,29(3):1-3.

