考虑转子电压电流耦合全补偿的双馈感应发电机改进PI-R电流控制策略

秦世耀 ，刘其辉 ，宋诗雨 ，李少林 ，赵亚男

（1.中国电力科学研究院 新能源与储能运行控制国家重点实验室，北京 100192；2.华北电力大学 新能源电力系统国家重点实验室，北京 102206）

0 引言

近年来，电网电压不对称情况下，双馈感应发电机（DFIG）高性能控制的研究逐渐增多［1-3］，而电网含有谐波时，DFIG风电机组高性能控制策略的研究相对较少。文献［4］的研究表明，电网谐波电压的存在会造成电机电磁转矩的脉动，增加铜耗和铁耗，引起定子、转子电流畸变，使输出功率、转矩脉动，严重时可能导致机组从电网中解列。目前国内外已有部分论文对电网谐波环境下双馈风力发电系统的运行与控制进行了研究，如基于多重同步旋转坐标系的定子电流谐波补偿方法［5-6］、加入谐波指令计算的多目标控制方法［7-9］、基于多重旋转坐标系的谐波电流控制方法［10-12］、基于谐振控制器的选择谐波消去方法［13-16］。以上文献采用的方法大致可以分为2类：一类是选定控制目标后，分别在同步速、-5倍同步速、+7倍同步速旋转的多重坐标系下采用PI控制器对转子电流进行控制，可称为基于多重旋转dq坐标系下PI电流控制器的控制策略；另一类是在统一的同步速旋转dq坐标系下采用PI-R控制器对转子电流进行控制，可称为基于dq坐标系下PI-R电流控制器的控制策略。但上述文献所提的各种方法大都忽略了转子电压、电流间的交叉耦合特性，有的则是仅考虑了转子基波电压、电流之间的耦合而没有考虑谐波电压、电流之间的耦合，因而所采取的补偿也不是“全补偿”。如果在d、q轴转子电流控制器的设计中没有对上述耦合进行有效补偿，则会影响转子电流控制的快速性和准确性，从而降低控制策略的动态特性。

基于以上原因，本文考虑转子电压、电流耦合特点对现有的控制策略进行改进。首先对电网谐波环境下DFIG动态建模，进而得到了各次谐波电压、电流之间的耦合关系，通过增加转子各次谐波电压、电流耦合补偿项，提出了基于dq坐标系下PI-R电流控制器的改进控制策略，并在PSCAD／EMTDC上进行了仿真验证。

1 电网谐波环境下DFIG动态建模

同步速旋转dq坐标系下DFIG数学模型矢量形式表达如下。

a.电压方程。

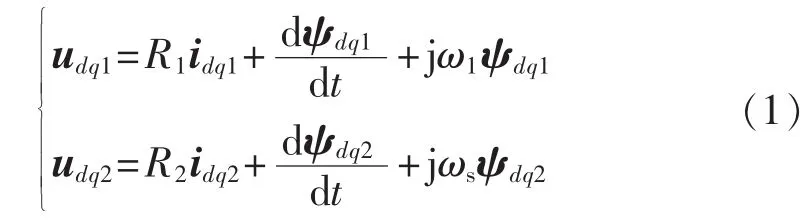
其中，udq1、udq2分别为定、转子电压；R1、R2分别为定、转子绕组的等效电阻；idq1、idq2分别为定、转子电流；ψdq1、ψdq2分别为定、转子磁链；ω1为同步转速；ωr为转子转速；ωs=ω1-ωr为同步转速相对于转子转速的转差角速度。

b.磁链方程。

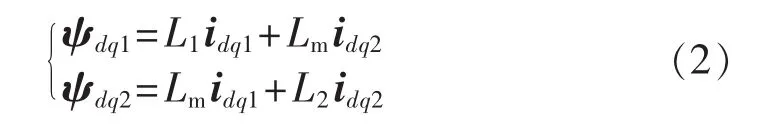
其中，Lm为dq坐标系下在同一轴上定子绕组与转子绕组之间的等效互感；L1为dq坐标系下定子绕组的自感；L2为dq坐标系下转子绕组的自感。

由式（2）整理得：

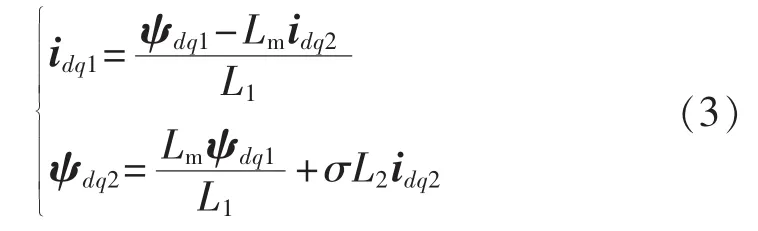
其中，σ=1-L2m／（L1L2），为漏磁系数。

将式（3）代入式（1），得到转子电压与转子电流之间的关系为：

在考虑5次负序谐波与7次正序谐波的三相电网畸变电压时，DFIG的建模将变得略微复杂。

1.1 考虑谐波时DFIG的电压与磁链方程

在电网电压含有5、7次谐波分量时，电网电压可表示为：

其中为电网电压在dq坐标系下的基波分量；为电网电压在－5dq坐标系下的5次谐波分量；为电网电压在+7dq坐标系下的7次谐波分量。式（5）还表明，在dq坐标系下，电网电压基波分量呈现为直流量，5、7次谐波分量分别呈现为以+6ω1、-6ω1旋转的交流量。

可得定子、转子电压方程［13］为：

其中，ω5s=5ω1+ωr；ω7s=7ω1-ωr。

定子、转子磁链方程为：

1.2 考虑谐波时DFIG的功率与电磁转矩方程

DFIG的电磁功率为：

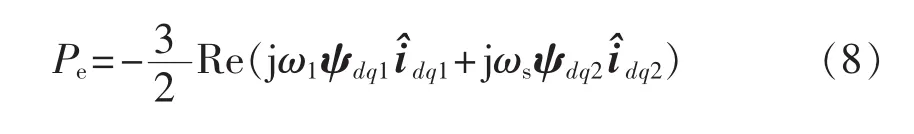
将电磁功率化简为只与定子磁链和转子电流有关的函数，得：

其中，Pe，dc为电磁功率的直流分量；Pe，sin6、Pe，cos6为电磁功率 6 次谐波分量的峰值；Pe，sin12、Pe，cos12为电磁功率12次谐波分量的峰值。上述各变量表达式参见文献［17］。

电磁转矩Te与电磁功率的关系为：

其中，pn为电机的极对数。

从以上公式中可以看出，当电网中含有5、7次电压谐波分量时，不仅定子电流会产生5、7次谐波，定子有功功率、无功功率与电磁转矩中还会出现6次以及12次谐波成分，这对于DFIG的运行是极为不利的。

2 电网谐波环境下DFIG改进控制策略

DFIG是一个存在大量交叉耦合现象的复杂机电系统，转子电压、电流之间的耦合会削弱控制系统的性能，若对转子电压、电流间的耦合进行有效补偿，将能够显著提高控制性能。本文全面考虑了转子基波和谐波电压、电流耦合并对此实现“全补偿”，对基于dq坐标系下PI-R电流控制器控制策略进行改进。

基于dq坐标系下PI-R电流控制器的控制策略虽然需要谐振控制器，但可以大幅减少PI控制器的数量。此外，在转子电流控制环路中，基于dq坐标系PI-R电流控制器的控制策略无需对转子电流进行基波与各次谐波分量的提取，减少了因谐波提取带来的控制延时，提高了控制的动态性能。

2.1 基于dq坐标系下PI-R电流控制器的改进控制策略

为能清晰表示出DFIG的耦合关系，将式（4）中的转子电压d、q轴分量分开写成式（11）。其中，GPIR（s）为 PI-R 控制器的传递函数；i*d2、i*q2分别为转子电流 d、q 轴参考值；Δud2、Δuq2为 dq 坐标系下转子电压的补偿项。式（12）为dq坐标系下转子电压解耦项，可通过PI-R控制器对转子电流指令值与实际值之差调节后输出。假定式（11）中微分项为零，机组稳态运行时定子磁链基波与各次谐波幅值不变，由式（11）可知转子电压全补偿项（包括基波、谐波补偿）如式（13）所示。

考虑转子电压、电流耦合全补偿的基于dq坐标系下PI-R电流控制器的改进控制策略如图1所示。

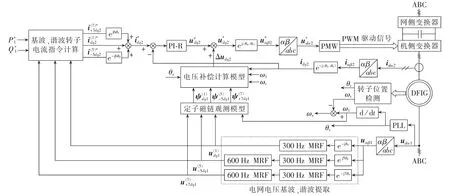
图1 考虑耦合全补偿的基于dq坐标系下PI-R电流控制器的改进控制策略Fig.1 Improved control strategy with complete coupling compensation for PI-R current controller based on dq coordinate system

其中分别为定子有功、无功功率参考值；θs为定子电压相角；θr为转子位置角。电网电压基波与谐波提取采用300 Hz与600 Hz陷波器MRF（Middle Reject Filter）组合提取。基波、谐波转子电流指令计算模块输出的转子电流dq坐标系下的基波指令坐标系下的 5 次谐波指令坐标系下的 7 次谐波指令被统一转换到dq坐标系上并合成为总电流指令值检测的转子电流无须经过基波与谐波分离直接变换到dq坐标系作为反馈值，两者的差值经过PI-R电流控制器调节得到补偿前的转子电压解耦项解耦项与电压补偿计算模型输出的转子电压耦合补偿项相加，得到dq坐标系下转子电压的指令值然后经过坐标变换变换到abc坐标系，最后通过PWM环节得到驱动机侧变流器IGBT器件的导通与关断的PWM脉冲信号，实现对DFIG指定控制目标下的功率与谐波控制。

进行补偿电压计算时需要知道定子磁链，因此控制策略中加入定子磁链观测模型，如图2所示。由式（13）可得到基于dq坐标系下的补偿电压计算模型如图3所示。

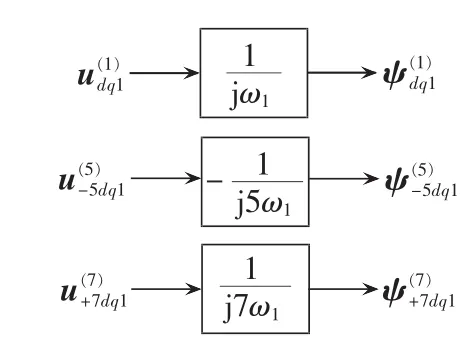
图2 定子磁链观测模型Fig.2 Stator flux observation model

2.2 PI-R电流控制器的设计方法

忽略定子电阻，由式（1）可得：

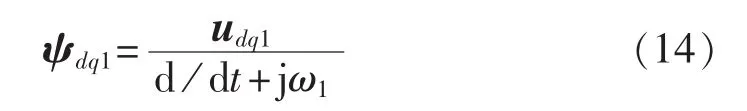
图3 补偿电压计算模型Fig.3 Compensating voltage calculation model

结合式（3）、（4）和（14）并进行拉氏变换，可得到DFIG控制模型的传递函数，即：

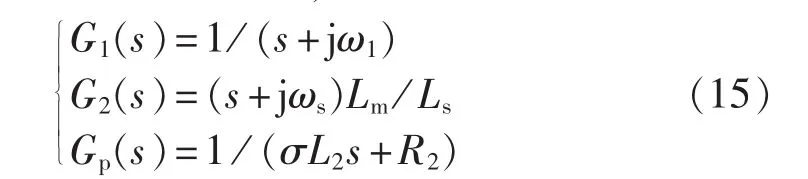
结合上述DFIG的数学模型与控制策略，能够得到 dq坐标系下双馈风力发电机控制系统的控制结构框图，如图4所示。图中Gd（s）为代表变流器动作延时的传递函数［18］，一般可认为延时时间Td等于采样周期，也等于开关周期的1／2，从第3节中变流器参数可知，本文采样周期为250 μs。

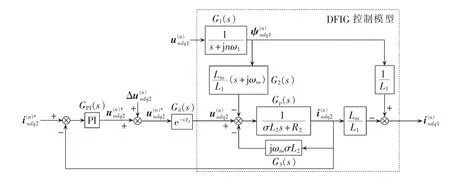
图4 dq坐标系下双馈风力发电机控制结构框图Fig.4 Block diagram of DFIG wind turbine control on dq coordinate system

PI-R控制器的传递函数为：

其中，KP为比例增益；KI为积分增益；KR为谐振控制器在谐振频率ω0处的增益；ωc为当KR=1时谐振控制器的开环截止频率。

忽略补偿项与耦合项，电流环结构框图如图5所示。

图5 双馈风力发电机控制系统电流环结构框图Fig.5 Block diagram of current loop of DFIG wind turbine control system

本文用ωcr表示开环穿越频率。令s=jωcr，转子侧时间常数τ=（σL2）／R2，可得转子电流开环传递函数在穿越频率ωcr处的频率特性表达式为：

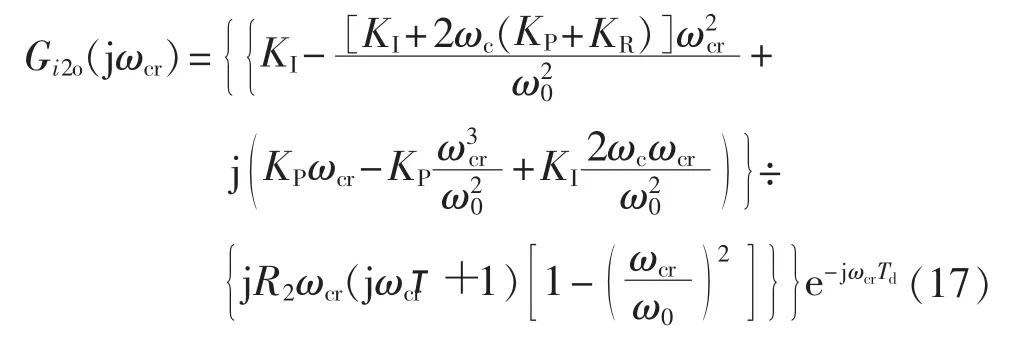
通常情况下，穿越频率ωcr略大于PI-R控制器的谐振频率 ω0，可认为两者近似相等［19］，故式（17）分子的实部中又因为故式（17）分子的虚部中此外，由于故式（17）分母中项可化简为综上，转子电流开环传递函数在穿越频率ωcr处的频率特性表达式可简化为：

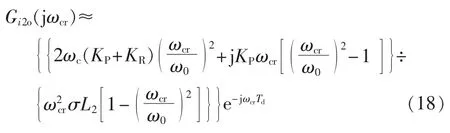
转子电流开环传递函数在穿越频率ωcr处的相位裕量φ表达式为：

在开环穿越频率处的开环传递函数增益应为1，即：

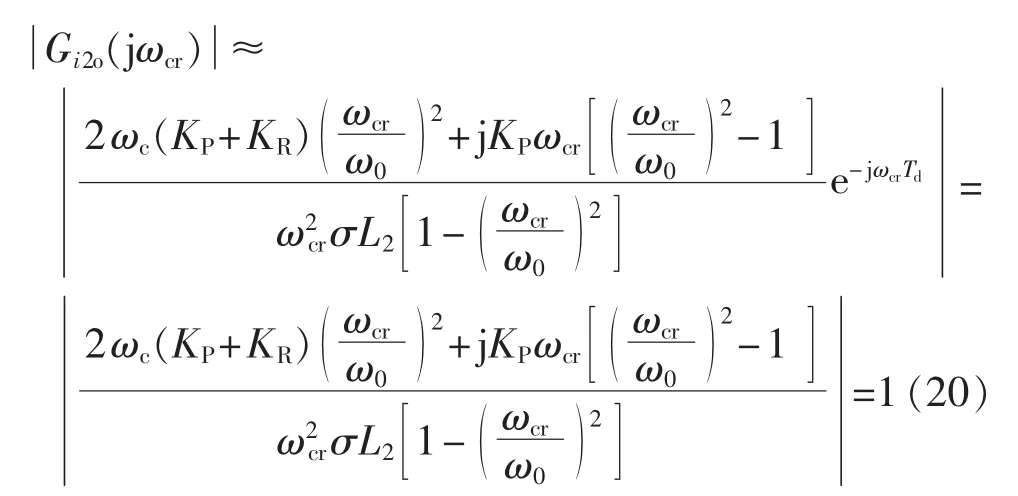
整理得到：

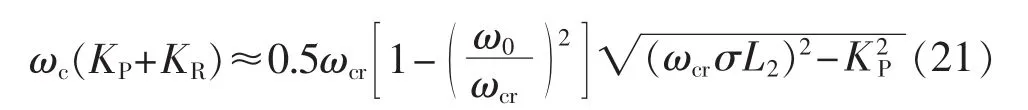
结合式（19）和式（21）可得：

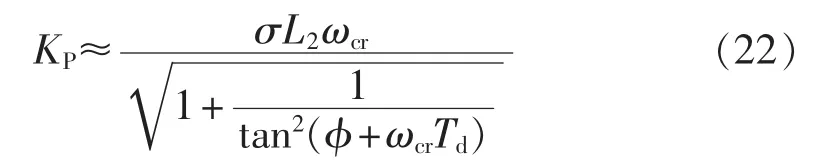
基于以上推导，dq坐标系下PI-R电流控制器的设计步骤如下：

a.选择合适的相位裕量和开环穿越频率，通常推荐的相位裕度 φ 在 30°～60°之间［20］，推荐的开环穿越频率ωcr在1／10～1／5的开关频率之间；

b.将设定好的相位裕度与开环穿越频率ωcr代入式（22）可解得PI-R控制器KP的参数值；

c. 将 KP、φ、ωcr代入式（19）可得到（KP+KR）ωc的值；

d.根据数字处理器的运算精度，选取较小的ωc值，通常推荐的PI-R控制器截止频率在2～10 rad／s之间［19］；

e.由已知的 KP、ωc、（KP+KR）ωc值计算出 KR；

f.在PI-R控制器中，PI控制器的参数主要对dq坐标系下的基波分量进行无静差控制，R控制器的参数在基波频率下影响很小，因此确定PI-R控制器中KI参数值时，可做近似处理使其与PI控制器中的KI参数值一致；

g.检查解得的PI-R参数是否满足控制系统的稳态与动态性能要求，若不满足，重新调整相位裕度、开环穿越频率与截止频率的选择，重复以上步骤，直至系统稳态与动态性能最优。

依照以上步骤，本文相位裕度φ选为30°，开环穿越频率 ωcr选为 1／6 的开关频率，即 333×2π（rad ／s），截止频率ωc选为5 rad／s，解得PI-R控制器的参数为KP＝18、KI＝405、KR＝942。

3 仿真验证

在PSCAD仿真平台中搭建双馈风力发电系统模型，系统参数［21］如下：风力机，额定功率为1.5 MW，叶片半径为35 m，空气密度为1.225 kg／m3，额定风速为 12m／s，切入风速为 3m ／s，切出风速为 25m／s；DFIG，额定功率为1.5 MV·A，转子定子比为2.5，极对数为 2，惯性常数为 1.14 s，定子电阻 R1＝0.00698 Ω，转子电阻 R2＝0.008252 Ω，定子漏抗 X1σ＝0.05618 Ω，转子漏抗 X2σ＝0.036818 Ω，定转子之间互感抗 Xm＝1.485432 Ω；变流器，直流母线电压为1100 V，开关频率为2 kHz，网侧进线电感为2 mH，网侧进线电阻为 0.0003 Ω，直流储能电容为 8640 μF。

为了验证考虑DFIG转子电压、电流耦合而加入的补偿项对发电机控制性能是否有优化作用，选择在dq坐标系下，对同一模型分别采用传统控制策略、加入补偿的PI-R电流控制器改进控制策略对DFIG进行控制，其中传统控制策略指未考虑电网谐波的理想情况下DFIG控制策略。通过仿真比较，可以验证加入补偿的基于dq坐标系下PI-R电流控制器的改进控制策略较传统控制策略在电网谐波环境中控制性能的优越性。

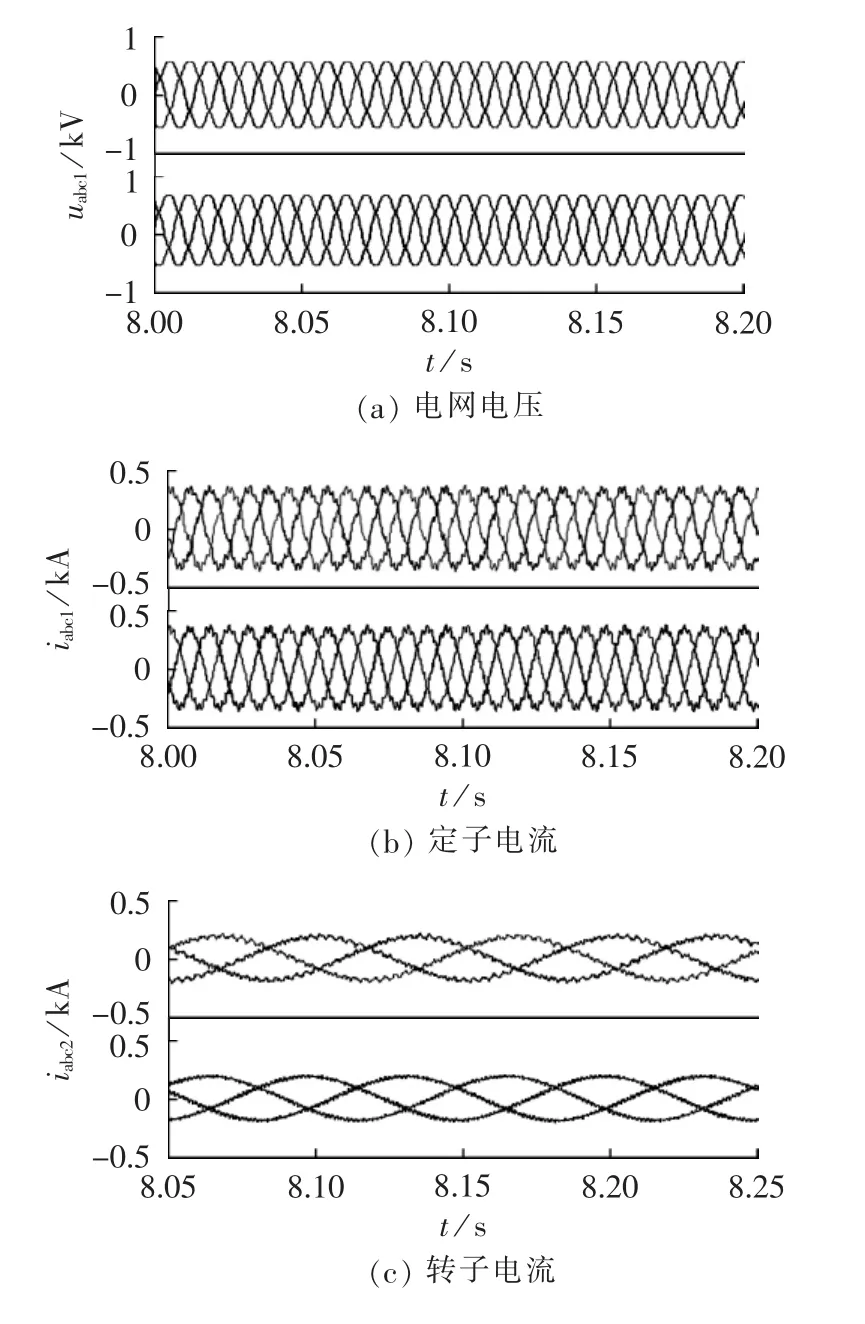
仿真中保持风速为6m／s不变，仿真总时长20s，DFIG运行于亚同步状态，转子转速约为0.8 p.u.，定子无功功率指令为0 var。电网畸变电压包括4%的5次负序谐波分量（每相谐波电压为4%＝0.015 9（kV））和4%的7次正序谐波分量，电网电压的总谐波畸变率（THD）约为5.66%，PI-R电流控制器的参数参照2.2节中的设计值。以平衡的转子电流为控制目标来进行仿真，不同控制策略下的仿真波形图与波形频谱分析图如图6、图7所示。图6中每个子图从上至下分别为采用传统PI控制、加入补偿的PI-R控制策略的仿真波形图；图7中每个子图从上至下分别为采用传统PI控制、加入补偿的改进PI-R电流控制策略的频谱分析图。

图6 以平衡的转子电流为控制目标时不同控制策略的波形图Fig.6 Waveforms of rotor current balancing control by two control strategies

图7 以平衡的转子电流为控制目标时不同控制策略的波形频谱分析图Fig.7 Spectrum analysis charts of rotor current balancing control by two control strategies

由波形图可以定性地看出不同控制策略下的仿真结果，频谱分析图则可以定量地看出不同控制策略的控制效果。其中频谱分析图中的数值为某次谐波的有效值。

以平衡的转子电流为控制目标时，由图6、图7可以得出以下结论（此处定义控制策略的电流谐波抑制效果为改进后的控制策略下电流d、q轴谐波的平方和根与传统控制策略下电流d、q轴谐波的平方和根之比）。

a.加入补偿后，基于dq坐标系下PI-R电流控制器的控制策略与传统控制策略相比降低了定子电流中5、7次谐波电流含量，同时加入补偿的定子电流谐波抑制效果为22.9%，使定子电流波形更趋于良好的正弦波形。

b.加入补偿后，基于dq坐标系下PI-R电流控制器的控制策略较传统控制策略能对转子电流d轴分量6次谐波进行明显的抑制，使转子电流波形更趋于良好的正弦波形。以平衡的转子电流为目标时，加入补偿的转子电流谐波抑制效果为1.5%，说明补偿后对转子电流的谐波抑制效果较对定子电流的谐波抑制效果更为显著。

c.加入补偿后，基于dq坐标系下PI-R电流控制器的控制策略与传统控制策略相比降低了定子无功功率中6、12次谐波电流含量，使定子无功功率波形更趋于平直。加入补偿后定子无功功率脉动抑制效果为45.2%，说明以平衡的转子电流为目标对定子无功功率的谐波抑制效果较对转子电流的谐波抑制效果弱很多。

4 结论

本文在电网谐波环境下对DFIG进行动态建模，在此基础上给出了包括基波和谐波在内的转子电压和电流耦合关系，通过对耦合进行全补偿给出了基于dq坐标系下PI-R电流控制器的改进控制策略。此外，建立了DFIG控制模型，提出了根据开环传递函数相位裕度和穿越频率设计PI-R控制器参数的方法和过程。理论分析和仿真验证表明，在电网谐波环境下，考虑DFIG转子电压、电流耦合的改进控制策略较传统与未改进的控制策略相比，可以更有效地抑制电网谐波对双馈风电机组带来的影响。以平衡的转子电流为控制目标时，转子电流中的谐波分量被有效控制，同时定子电流、定子有功、无功功率的谐波分量也随着转子电流谐波的抑制而在一定程度上得到抑制。

参考文献：

［1］WANG Yi，XU Lie.Coordinated control of DFIG and FSIG-based wind farms under unbalanced grid conditions［J］.IEEE Transactions on Power Delivery，2010，25（1）：367-377.

［2］YAO Jun，LIHui，CHEN Zhe，etal.Enhanced controlofa DFIG-based wind-power generation system with series grid-side converterunderunbalanced grid voltageconditions［J］.IEEE Transactions on Power Electronics，2013，28（7）：3167-3181.

［3］KEARNEY J，CONLON M F，COYLE E.The integrated control of the rotor side and grid side converters in a DFIG to reduce both power and torque pulsations during network voltage unbalance conditions［C］∥2009 44th International Universities Power Engineering Conference（UPEC）.Glasgow，England：［s.n.］，2009：1-5.

［4］EMANUEL A E.Estimating the effects of harmonic voltage fluctuations on the temperature rise of squirrel-cage motors［J］.IEEE Transactions on Energy Conversions，1991，6（1）：161-168.

［5］RAMOS C J ，MARTINS A P，CARVALHO A S.Rotor current controllerwith voltage harmonicscompensation fora DFIG operating under unbalanced and distorted stator voltage［C］∥IECON 2007-33rd Annual Conference of the IEEE Industrial Electronics Society.Taipei，China：IEEE，2007：1287-1292.

［6］徐君，陈文杰，徐德鸿，等.电网低次谐波电压下双馈风电系统定子谐波电流抑制［J］. 电力系统自动化，2011，35（8）：87-92.XU Jun，CHEN Wenjie，XU Dehong，etal.Statorharmonic current suppression of DFIG in wind power system under low order harmonic voltage of power grid［J］.Automation of Electric Power Systems，2011，35（8）：87-92.

［7］QUAN Yu，NIAN Heng，HU Jiabing，et al.Improved control of the grid-connected converter under the harmonically distorted grid voltage conditions［C］∥2010 InternationalConferenceon Electrical Machines and Systems.Incheon，Korea： ［s.n.］，2010：204-209.

［8］HU Jiabing，NIAN Heng，XU Hailiang，et al.Dynamic modeling and improved controlofDFIG underdistorted grid voltage conditions［J］.IEEE Transactions on Energy Conversion，2011，26（1）：163-175.

［9］胡家兵，贺益康，郭晓明，等.不平衡电压下双馈异步风力发电系统的建模与控制［J］. 电力系统自动化，2007，31（14）：47-56.HU Jiabing，HE Yikang，GUO Xiaoming，et al.The unbalanced voltage of DFIG in wind power system modeling and control［J］.Automation of Electric Power Systems，2007，31（14）：47-56.

［10］BLAABJERG F，TEODORESCU R，LISERRE M，et al.Overview ofcontroland grid synchronization fordistributed power generation systems［J］.IEEE Transactions on Industrial Electronics，2006，53（5）：1398-1409.

［11］张树全，戴珂，谢斌，等.多同步旋转坐标系下指定次谐波电流控制［J］. 中国电机工程学报，2010，30（3）：55-62.ZHANG Shuquan，DAI Ke，XIE Bin，et al.Synchronous rotating coordinate system specified harmonic current control［J］.Proceedings of the CSEE，2010，30（3）：55-62.

［12］姚骏，夏先锋，陈西寅，等.风电并网用全功率变流器谐波电流抑制研究［J］. 中国电机工程学报，2012，32（16）：17-25.YAO Jun，XIA Xianfeng，CHEN Xiyin，et al.Study on harmonic current suppression of full power converter for wind power grid connected power converter［J］.Proceedings of the CSEE，2012，32（16）：17-25.

［13］徐海亮.双馈风电变流器的谐振控制技术研究［D］.杭州：浙江大学，2014.XU Hailiang.Research on resonantcontroltechnology of double fed wind power converter［D］.Hangzhou：Zhejiang University，2014.

［14］LISERRE M，TEODORESCU R，BLAABJERG F. Multiple harmonics control for three-phase grid converter systems with the use of PI-RES current controller in a rotating frame［J］.IEEE Transactions on Power Electronics，2006，21（3）：836-841.

［15］TRINH Q N，LEE H H.Improvement of current performance for grid connected converter under distorted grid condition［C］∥IET Conference on Renewable Power Generation（RPG 2011）.Edinburgh，England：［s.n.］，2011：1-6.

［16］贺益康，徐海亮.双馈风电机组电网适应性问题及其谐振控制解决方案［J］. 中国电机工程学报，2014，34（29）：5188-5203.HE Yikang，XU Hailiang.Adaptiveproblemsofthepower system of DFIG and its resonant control solution［J］.Proceedings of the CSEE，2014，34（29）：5188-5203.

［17］XU Hailiang，HU Jiabing，NIAN Heng，et al.Dynamic modeling and improved control of DFIG under unbalanced and distorted grid voltage conditions［C］∥2012 IEEE International Symposium on IndustrialElectronics.Hangzhou，China：IEEE，2012：1579-1584.

［18］KIM H，DENGER M W，GUERRERO J M，et al.Discrete-time current regulator design for AC machine drives［J］.IEEE Transactions on Industry Applications，2010，46（4）：1425-1435.

［19］刘昌金.适应电网环境的双馈风电机组变流器谐振控制［D］.杭州：浙江大学，2012.LIU Changjin.The resonantcontrolofDFIG in the grid environment［D］.Hangzhou：Zhejiang University，2012.

［20］MIRET J，CASTILLA M，MATAS J，et al.Selective harmoniccompensation control for single-phase active power filter with high harmonic rejection［J］.IEEE Transactions on Industrial Electronics，2009，56（8）：3117-3127.

［21］齐桓若.电网谐波环境下双馈风力发电机控制技术研究［D］.北京：华北电力大学，2015.QI Huanruo.Research on control technology of doubly fed wind power generator in power system harmonic environment［D］.Beijing：North China Electric Power University，2015.