模块化多电平换流器子模块均压电阻参数优化策略

李 超，唐志军，林国栋，林金东，林文彬，余斯航，蔡美杰

（国网福建省电力有限公司电力科学研究院，福建 福州 350007）

0 引言

目前国内已投运的柔性直流输电工程均采用模块化多电平换流器MMC（Modular Multilevel Converter）［1-4］，其子模块主要器件有绝缘栅双极型晶体管（IGBT）、储能电容、续流晶闸管、冗余开关、均压电阻、取能电源等。均压电阻并联在储能电容两端，一方面可在换流器启动过程中对各子模块电容进行均压，另一方面可在换流器停运后充当电容的放电电阻。均压电阻参数直接影响电容的均压效果和放电时间，但目前并没有文献介绍均压电阻的选取原则，因此有必要对均压电阻的参数设计提出理论依据和优化策略。

现有研究认为均压电阻主要在换流器启动阶段起到均压作用，且由于均压电阻阻值的误差较小，各子模块电压在启动阶段基本一致。文献［5-7］在分析换流器启动过程中均认为各子模块电压相等。而换流器解锁后可通过优化电容值、改进控制方式和环流控制等方法实现电容电压均压，均压电阻所起作用较小。文献［8］提出可降低电容值的控制策略，文献［9-10］提出子模块电容均压算法，文献［11-13］提出环流抑制算法可降低电容电压波动。现有研究认为均压电阻阻值大小对电容均压效果并无较大影响，其参数设计只需考虑电阻功率和停运后放电时间即可。但根据已投运的南汇、厦门等柔性直流输电工程实际运行数据可知：在换流器启动阶段，各子模块电容均压效果较差，与现有理论分析结果不符；且根据试验可知，均压电阻的大小直接影响电容均压效果。因此需要分析均压电阻影响电容均压效果的机理，从而提出均压电阻参数优化策略。

本文首先改进了现有子模块的仿真模型，增加了均压电阻、取能电源等实际器件，使其更接近于工程实际。在优化后子模块仿真模型的基础上，推导出均压电阻和取能电源等效电阻共同作用引起的电容电压变化过程，阐明了启动过程中电容电压均压效果劣化的机理。然后综合考虑均压效果、功耗和换流器放电时间的需求，提出均压电阻参数优化策略。最后依托厦门柔性直流输电工程给出设计实例并进行了试验验证，试验结果表明根据本文设计的均压电阻可满足均压效果、静态直流充电耐受时间、放电时间等因素的要求，证明了所提子模块均压电阻参数优化策略的有效性。

1 子模块仿真模型优化

为了便于扩展和替换，MMC子模块采用独立的单元结构设计。以目前国内柔性直流输电工程子模块采用的半桥拓扑为例［14-16］，一个子模块的基本结构如图1 所示，包含 IGBT 模块（VT1、VT2）、反向并联二极管（VD1、VD2）、续流晶闸管（SCR）、冗余开关（K）、储能电容（C）、均压电阻（R0）、取能电源（PW）、中央控制板（SMC）、驱动电路（GDU）、散热器（图中未画出）。

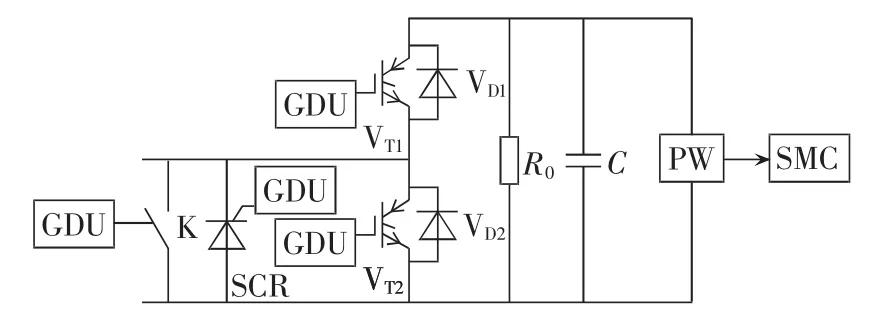
图1 子模块电路拓扑Fig.1 Circuit topology of sub-module

现有研究对子模块进行建模时通常只考虑IGBT、反向并联二极管和储能电容，其典型模型如图2（a）所示［17-18］。在启动过程中，由于 IGBT 闭锁，子模块仿真模型可进一步简化，简化后模型如图2（b）所示。根据图2中的子模块模型进行仿真时，无论均压电阻阻值大小，各子模块电容电压在启动过程中均保持一致，与工程中电容电压均压效果较差的实际情况不符。

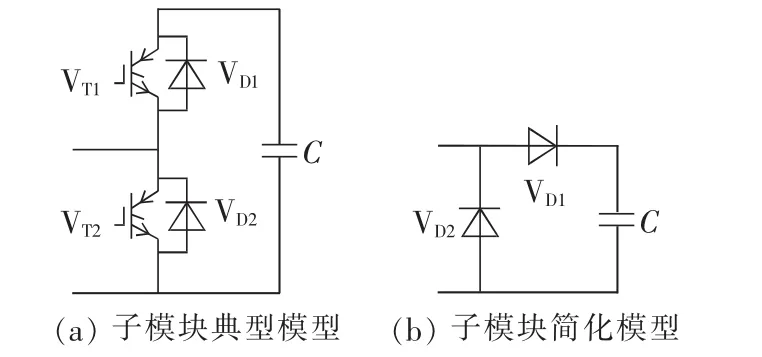
图2 子模块典型模型和简化模型Fig.2 Typical and simplified model of sub-module

由于现有子模块仿真模型无法分析启动过程中电容电压均压效果劣化的机理，需提出子模块仿真模型优化方法。在实际工程中，均压电阻和取能电源输入端均并联在储能电容两端。取能电源采用开关电源模式将电容电压转化为低压直流电为中央控制板和各驱动电路供能。取能电源等效电阻与均压电阻并联后直接影响各子模块电容电压的均压效果。现有模型忽略了均压电阻和取能电源对电容电压的影响，而本文通过增加均压电阻、取能电源等实际器件优化现有子模块仿真模型，使其更接近工程实际，优化后模型如图3所示。图中，UC为储能电容电压；r为取能电源等效电阻；R0为均压电阻；R为均压电阻与取能电源等效电阻并联后阻值。其中r并不是固定值，而是变量，其阻值与取能电源状态、中央控制板与驱动板卡的功率、电容电压值和取能电源效率有关。

图3 子模块优化后模型Fig.3 Optimized model of sub-module

当电容电压过低（低于取能电源启动电压）时，取能电源处于关闭状态，其等效电阻为MΩ级，即：

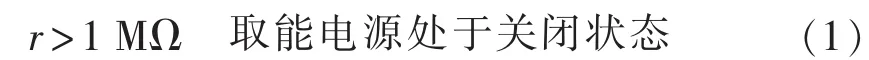
当取能电源处于工作状态时，其等效电阻为：

其中，P为中央控制板、IGBT驱动电路、续流晶闸管驱动电路、冗余开关驱动电路等板卡的总功率；η为取能电源效率。

均压电阻与取能电源等效电阻并联，其阻值为：

优化后的子模块仿真模型引入了均压电阻和取能电源等实际器件，为进一步分析均压电阻对电容均压效果的影响提供支撑。

2 启动过程中均压电阻对电容均压的影响

2.1 启动过程中换流器仿真模型

目前国内柔性直流输电工程均采用自励启动方式，即一端换流器通过对交流系统进行不控整流向子模块电容充电，另一端换流器处于静态直流充电状态。MMC处于不控整流或静态直流充电状态时，子模块IGBT均处于闭锁状态，各子模块电容电压完全由均压电阻和取能电源等效电阻决定。但均压电阻阻值和取能电源参数在实际工程中均存在差异，同时取能电源等效电阻随电压值不同发生动态变化，两者共同作用于电容均压过程，使电容电压均压效果发生劣化。其中，MMC处于静态直流充电状态时，由于每相上下桥臂的子模块共同对直流母线电压分压，子模块平均电压较低，此时均压效果劣化程度最高。

现以MMC处于静态直流充电状态时某一相为例分析电容电压变化过程，其仿真模型如图4所示。图中，ik为流入第k个子模块电容的电流；UCk为第k个子模块电容电压；rk为第k个子模块取能电源等效电阻实时值；Rk为第k个子模块均压电阻与取能电源等效电阻并联后阻值；i为桥臂电流；各子模块均压电阻R0和储能电容C参数一致。

图4 静态直流充电时的仿真模型Fig.4 Simulation model of static DC charging process

由于各子模块串联，流入各子模块的电流均等于桥臂电流，根据基尔霍夫电流定律可知：

在t0—t1时间段内，子模块电容电压变化量为：

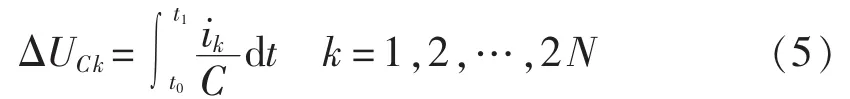
由于直流母线电压基本保持不变，各子模块电容电压变化量总和约为0，即：

由于储能电容容值较大，当t0—t1时间段较小时，可认为该时间段内电流值恒定，即式（5）转化为：

将式（7）代入式（6）可得：

对式（4）求和可得：

将式（8）代入式（9）可得：

当已知t0时刻各子模块电容电压、均压电阻和取能电源等效电阻时，联立式（4）、（10）可得：

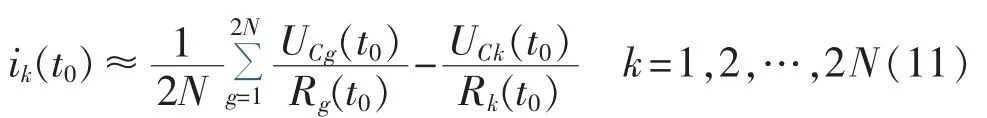
将式（11）代入式（7）可得：

则第k个子模块在t1时刻的电容电压值为：

将式（1）—（3）代入式（13），得到均压电阻和取能电源等效电阻与电容电压的关系如下。

a.取能电源处于关闭状态。

取能电源等效电阻为固定值，与取能电源输入端之间的绝缘能力有关，其阻值为MΩ级。此时电容电压计算公式为：

b.取能电源处于工作状态。

取能电源等效电阻为变量，与电容电压、取能电源效率和中央控制板功率有关。此时电容电压计算公式为：

仿真过程中只需设定各子模块电容电压的初始值、均压电阻和时间区间，即可根据式（14）或式（15）通过叠代求解的方式仿真均压电阻和各子模块电容电压变化过程的关系，具体仿真流程如图5所示。

图5 电容均压流程图Fig.5 Flowchart of capacitor voltage balancing

2.2 均压电阻阻值对电容均压效果的影响

以厦门柔性直流输电工程为例，MMC处于不控整流充电状态时虽然有限流电阻限流，但其时间常数为0.56s，在交流断路器闭合1s左右时直流母线电压即可达到稳定值。由于子模块工作时间较短，各子模块电容电压初始值基本保持一致。因此设定各子模块电容电压初始值一致，仿真分析均压电阻不同阻值时的电容电压变化过程。

a.均压电阻阻值较大时。

均压电阻远大于取能电源等效电阻时，两者并联后阻值主要由取能电源等效电阻决定。但由于产品一致性问题，各子模块取能电源等效电阻初始值存在一定差异，取能电源等效电阻初始值较小的子模块电容放电从而使电压降低；随着电压降低，其等效电阻减小，进一步使其分配的电压降低；如此循环使此部分子模块电压不断降低，当低于取能电源关断电压后进入反复启停状态。而取能电源等效电阻初始值较大的子模块电容充电从而使电压不断升高。其中4个典型子模块的仿真波形如图6所示，图中电容电压不断升高的是取能电源等效电阻初始值较大的子模块；电容电压不断降低、最终进入反复启停状态的是取能电源等效电阻初始值较小的子模块。

b.均压电阻阻值较小时。

均压电阻远小于取能电源等效电阻时，两者并联后阻值主要由均压电阻决定。由于均压电阻并不随电压变化，而取能电源等效电阻的动态变化带来的电压波动较小，最终使子模块电容电压形成动态平衡。其中4个典型子模块的仿真波形如图7所示，图中电容电压升高的是取能电源等效电阻初始值较大的子模块；电容电压降低的是取能电源等效电阻初始值较小的子模块；最终各子模块电压基本保持稳定状态。

图6 均压电阻较大时电压波形Fig.6 Voltage waveforms with larger balancing resistor

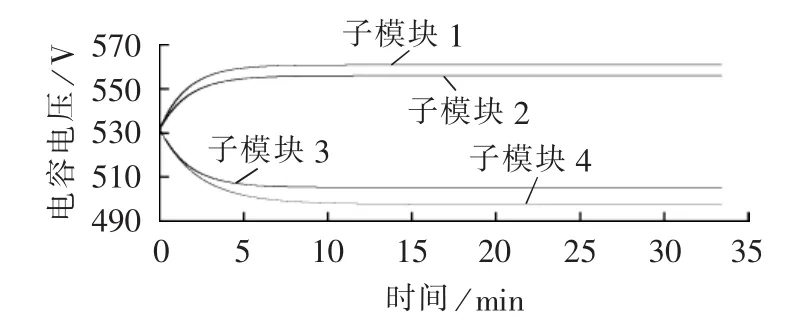
图7 均压电阻较小时电压波形Fig.7 Voltage waveforms with smaller balancing resistor

可见，均压电阻的阻值大小直接影响启动过程中子模块电容电压均压效果。当均压电阻阻值远大于其取能电源等效电阻时，电容均压效果较差，部分子模块甚至因电压跌落而反复启停。因此从提升启动过程电容均压效果方面考虑，均压电阻阻值越小越好。

3 均压电阻参数优化设计

均压电阻的常规参数设计方法只考虑了放电时间与功率的要求，忽略了均压电阻阻值对电容均压效果的影响。均压电阻与取能电源输入端并联在电容两端，均压电阻参数应与取能环节参数相匹配，才能满足MMC启动过程中电容均压的要求。因此均压电阻参数具体优化设计时需要考虑以下3个方面。

（1）电容均压。

当均压电阻与取能环节参数不匹配时，MMC启动过程中将出现电容均压效果劣化的情况：一方面导致大量子模块处于反复启停状态，使其取能电源易因反复启停产生的过电压或过电流导致故障；另一方面使剩余子模块因电压过高产生过压故障。因此，均压电阻与取能环节参数匹配的原则是使MMC即使处于静态直流充电状态时，反复启停的子模块所占比例亦不超过50%。

MMC启动时一方面要考虑调度指令下达、执行、核对等步骤所需的最低时间；另一方面要防止MMC长期处于静态直流充电状态，避免电容均压情况过度劣化。因此在柔性直流输电保护系统中设置了静态直流充电耐受时间保护定值，MMC应在此时间内完成启动过程，且在此时间定值内反复启停的子模块数量不应超过子模块总数量的50%。综上所述，启动过程中对子模块电容均压的基本要求为：

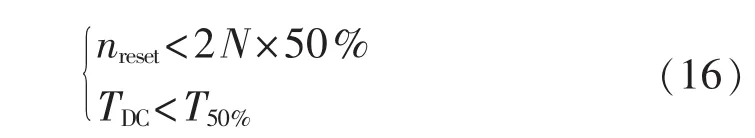
其中，nreset为处于反复启停状态的子模块数量；TDC为静态直流充电耐受时间保护定值；T50%为反复启停的子模块数量所占比例达到50%所需的时间。

根据图4仿真模型、图5仿真流程以及式（16），均压电阻与取能环节参数匹配设计的具体步骤如下。

a.采集各子模块电容容值、取能电源效率、二次控制板卡功率、静态直流充电时子模块电容电压初始值等数据。

b.根据图4建立MMC静态直流充电仿真模型，并输入采集的工程具体参数。

c.从小至大设定不同的均压电阻阻值并依次仿真，仿真得到反复启停子模块数量所占比例达到50%所需的时间T50%。

d.随着均压电阻阻值增大，电容均压劣化情况加重、T50%不断减小。当T50%＜TDC时，已不满足式（16）所示要求，此时仿真结束并最终确定满足式（16）的均压电阻上限值 Rmax1。

（2）放电时间。

换流器停运（尤其是因故障导致的紧急停运）后，检修人员需进入阀厅进行故障处理工作，但在电容放电完全前其门禁系统处于闭锁状态。门禁闭锁时间由换流器的放电时间决定。目前对子模块电容放电时间的研究中只考虑了均压电阻的作用，忽略了取能电源工作消耗的能量，导致放电时间误差较大。本文根据优化后子模块模型分析放电过程的2个阶段。

a.取能电源工作，由取能电源和均压电阻一起放电。此阶段放电时间为：

其中，UN为换流器解锁后子模块额定工作电压；Uoff为取能电源关断电压阈值。

b.取能电源关断，由均压电阻进行放电。此阶段放电时间为：

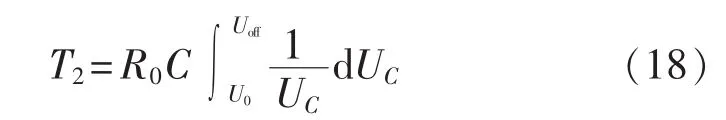
其中，U0为子模块电容电压安全阈值。

放电时间为两阶段时间之和，且需满足在门禁系统闭锁时间内电容应放电完毕的条件，即：

其中，Toff为换流器停运后阀厅门禁系统闭锁时间。

联立式（17）—（19）可计算均压电阻满足放电时间需求的另一上限值Rmax2。

（3）功率。

根据电容均压和放电时间的需求，可确定均压电阻参数设计应满足的条件为：

根据仿真可知均压电阻阻值越小，电容均压效果越好、放电时间越短。但在满足电容均压和放电时间要求时，还需考虑电阻的功率及散热要求。为了降低子模块功耗和对水冷系统的负荷，均压电阻应尽量选取较大的阻值。

综上所述，均压电阻参数设计时根据式（20）选取最大阻值，可同时满足电容均压、放电时间和功率要求。

4 设计实例与试验验证

4.1 厦门柔性直流输电工程均压电阻参数设计实例

依托厦门柔性直流输电工程给出均压电阻参数设计实例，实例中涉及的具体参数包括子模块数量、额定电压、板卡总功率、取能电源效率及启动/关断电压、静态直流充电耐受时间定值和换流器停运后阀厅门禁系统闭锁时间定值等，具体数值如下：每桥臂模块数为216，电容为10mF，子模块额定电压为1.6 kV，各板卡总功率为13~15 W，直流充电时电容电压为532V，取能电源启动电压为350V，取能电源关断电压为450 V，取能电源效率为0.65~0.75，门禁系统闭锁时间为60min，静态直流充电耐受时间为20min，子模块电压安全阈值为1V。

根据以上参数建立仿真模型，将均压电阻设置为不同阻值，仿真得到反复启停子模块数量所占比例达到50%所需时间T50%的数值，仿真结果如表1所示。由于MMC静态直流充电耐受时间保护定值设置为20 min，根据式（16）和表1数据可知，均压电阻的上限值Rmax1选取20~30kΩ为宜。

厦门柔性直流输电工程换流器停运后阀厅门禁系统闭锁时间定值为1h，子模块电容电压安全阈值为1V。以1V数值进行仿真得到放电时间和均压电阻的关系如图8所示。根据图8和式（19）可知，为满足闭锁时间1h的条件，均压电阻的另一上限值Rmax2为56kΩ（此数值亦是均压电阻常规设计方法确定的阻值）。

综上所述，综合考虑均压效果和放电时间的要求，根据式（20）确定厦门柔性直流输电工程子模块均压电阻阻值为25 kΩ。在额定电压1 600 V时均压电阻功率为102.4 W，考虑到电压波动和冗余设计，均压电阻功率设计为300 W。均压电阻参数最终设计值为：阻值25kΩ，额定功率300W，误差1%。

表1 均压电阻与T50%的关系Table 1 Relationship between balancing resistor and T50%

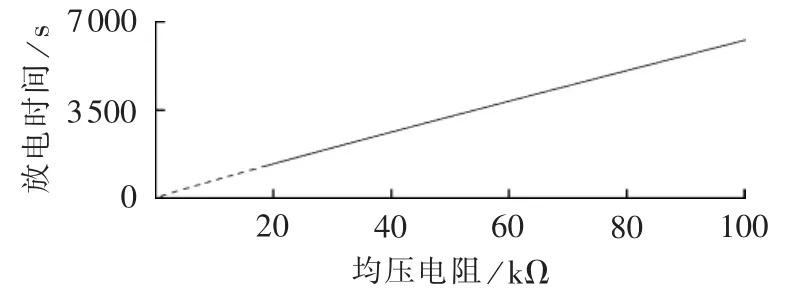
图8 均压电阻与放电时间的关系Fig.8 Relationship between balancing resistor and discharge time

4.2 试验验证

a.根据均压电阻参数设计实例，依托厦门柔性直流输电工程进行静态直流充电试验。

浦园站处于不控整流状态、鹭岛站处于静态直流充电状态时，鹭岛站换流器中2个子模块反复启停的波形如图9所示。由图9可知，在静态直流充电时子模块电容电压的确发生均压劣化问题，部分子模块电压跌落甚至反复启停，证明了本文均压电阻阻值在启动过程中对子模块电容电压影响机理分析的正确性。

图9 子模块反复启停时试验波形Fig.9 Experimental waveforms of sub-modules in repeated start-up and shutdown

鹭岛站MMC处于静态直流充电状态时，根据均压电阻常规设计方法确定的阻值56 kΩ进行试验时，只需15min即有50%子模块处于反复启停状态且所占比例不断提升，不满足电容均压要求。而根据本文所提均压电阻参数优化策略确定的阻值25 kΩ进行试验时，其反复启停的子模块试验数据如表2所示，反复启停子模块数量所占比例达到50%所需时间T50%的数值为20~25min，满足 MMC静态直流充电耐受时间保护定值要求范围，证明了本文均压电阻参数设计方法的正确性。

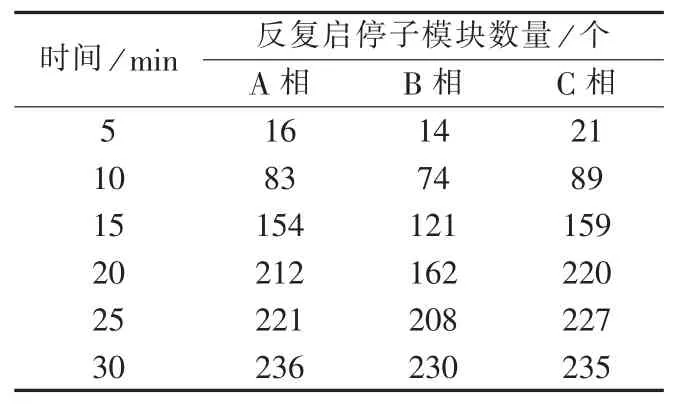
表2 反复启停子模块数量Table 2 Quantity of sub-modules in repeated start-up and shutdown

b.双端MMC均解锁后空载运行，各子模块电容电压基本维持在1 600 V。此时MMC进行紧急停运，完成子模块电容放电试验。

放电试验时，其中2个子模块电容电压随放电时间变化的波形如图10所示。由图10可见，本文提出的放电仿真模型可体现取能电源及其负载在放电过程中的作用，使仿真结果与试验波形基本一致。子模块电容电压和放电时间具体数值如表3所示。由表3可见，在换流器停运1 h内子模块电容电压低于1 V，证明本文提出的均压电阻参数设计方法满足放电时间的要求。

图10 电容电压随放电时间的变化波形Fig.10 Waveform of capacitor voltage vs.discharge time

表3 MMC停运后放电时间与电容电压Table 3 Discharge time and capacitor voltage after outage of MMC

5 结论

a.本文通过引入均压电阻、取能电源等效电阻参数优化子模块仿真模型，使其更接近工程实际。

b.根据优化后子模块模型，仿真分析了均压电阻在MMC启动过程中对电容均压的影响。阐明了均压电阻远大于取能电源等效电阻时电容均压效果劣化的机理。电容均压劣化导致部分子模块电压过高，部分子模块电压跌落甚至反复启停。

c.修正了MMC停运过程中放电时间的计算方法，体现了取能电源及其负载在放电过程中的作用，使放电时间更接近试验结果。

d.根据电容均压、放电时间以及功率等方面的要求，提出了均压电阻参数优化策略。根据静态直流充电耐受时间和停运后门禁闭锁时间2个保护定值仿真和计算得到均压电阻阻值上限，同时综合考虑功率和冷却要求将其阻值确定在上限附近。

e.依托厦门柔性直流输电工程给出了均压电阻参数设计实例并进行了相关试验。试验结果表明根据本文设计的均压电阻满足均压、静态直流充电耐受时间、放电时间和功率等方面的需求，证明了所提均压电阻参数优化策略的有效性。

致 谢

本文相关试验得到了厦门柔性直流输电换流站（鹭岛站、浦园站）、南瑞集团、全球能源互联网研究院、中电普瑞电力工程有限公司等单位运行人员与研发人员的大力支持，特此表示感谢。

参考文献：

［1］王姗姗，周孝信，汤广福，等.模块化多电平电压源换流器的数学模型［J］.中国电机工程学报，2011，31（24）：1-8.WANG Shanshan，ZHOU Xiaoxin，TANG Guangfu，et al.Modeling of modular multi-level voltage source converter［J］.Proceedings of the CSEE，2011，31（24）：1-8.

［2］张建坡，田新成，尹秀艳.模块化多电平换流器直流输电控制策略［J］.电力自动化设备，2015，35（11）：103-108.ZHANG Jianpo，TIAN Xincheng，YIN Xiuyan.Control strategy of MMC-HVDC［J］.Electric Power Automation Equipment，2015，35（11）：103-108.

［3］喻锋，王西田.基于冒泡原理的模块化多电平换流器快速电压均衡控制策略［J］.电力自动化设备，2015，35（9）：81-86.YU Feng，WANG Xitian.Fast voltage balancing control based on bubbling principle for modular multilevel converter［J］.Electric Power Automation Equipment，2015，35（9）：81-86.

［4］汤广福，贺之渊，庞辉.柔性直流输电工程技术研究、应用及发展［J］.电力系统自动化，2013，37（15）：3-14.TANG Guangfu，HE Zhiyuan，PANG Hui.Research，application and developmentofVSC-HVDC engineering technology［J］.Automation of Electric Power Systems，2013，37（15）：3-14.

［5］刁冠勋，李文津，汤广福，等.适用于风电并网的模块化多电平柔性直流启动控制技术［J］.电力系统自动化，2015，39（5）：81-87.DIAO Guanxun，LI Wenjin，TANG Guangfu，et al.Start-up control technology of modular multilevel VSC-HVDC system for wind farm integration［J］.Automation of Electric Power Systems，2015，39（5）：81-87.

［6］孔明，邱宇峰，贺之渊，等.模块化多电平式柔性直流输电换流器的预充电控制策略［J］.电网技术，2011，35（11）：67-73.KONG Ming，QIU Yufeng，HE Zhiyuan，et al.Pre-charging control strategies of modular multilevel converter for VSC-HVDC［J］.Power System Technology，2011，35（11）：67-73.

［7］肖晃庆，徐政，薛英林，等.多端柔性直流输电系统的启动控制策略［J］.高电压技术，2014，40（8）：2550-2557.XIAO Huangqing，XU Zheng，XUE Yinglin，et al.Start control strategy of MMC-MTDC system［J］.High Voltage Engineering，2014，40（8）：2550-2557.

［8］杨文博，宋强，刘文华，等.降低模块化多电平换流器子模块电容值的控制方法［J］.电力系统自动化，2015，39（16）：86-94.YANG Wenbo，SONG Qiang，LIU Wenhua，etal.A control strategy for reducing submodule capacitance value of modular multilevel converter［J］.Automation of Electric Power Systems，2015，39（16）：86-94.

［9］ZHANG Y，ADAM G P，LIM T C，et al.Analysis of modular multilevel converter capacitor voltage balancing based on phase voltage redundant states［J］.IET Power Electronics，2012，5（6）：726-738.

［10］孔明，汤广福，贺之渊，等.基于子模块电容电压预估的MMC分段电压平衡优化控制［J］.高电压技术，2015，41（7）：2457-2463.KONG Ming，TANG Guangfu，HE Zhiyuan，et al.Optimization control of sub-module capacitor voltage balance for modular multilevel converter based on the capacitor voltage estimation and segmented design［J］.High Voltage Engineering，2015，41（7）：2457-2463.

［11］WANG Kui，LI Yongdong，ZHENG Zedong，et al.Voltage balancing and fluctuation-suppression methods of floating capacitors in a new modular multilevel converter［J］.IEEE Transactions on Industrial Electronics，2013，60（5）：1943-1954.

［12］刘焕，岳伟，张一工，等.基于准比例-谐振控制的MMC-HVDC环流抑制策略［J］.电力系统自动化，2015，39（12）：146-151.LIU Huan，YUE Wei，ZHANG Yigong，et al.Circuiting current restraining strategy based on quasi proportional-resonance control in MMC-HVDC［J］.Automation of Electric Power Systems，2015，39（12）：146-151.

［13］张明，吴浩伟，蔡凯，等.模块化多电平变换器的环流谐波抑制策略［J］.电工技术学报，2015，30（21）：57-66.ZHANG Ming，WU Haowei，CAI Kai，et al.Circulating harmonics suppression method for modular multilevel converter［J］.Transactions of China ElectrotechnicalSociety，2015，30（21）：57-66.

［14］LI Binbin，ZHANG Yi，WANG Gaolin，et al.A modified modular multilevel converter with reduced capacitor voltage fluctuation［J］.IEEE Transactions on Industrial Electronics，2015，62（10）：6108-6119.

［15］SHI Xiaojie，LIU Bo，WANG Zhiqiang，et al.Modeling，control design，and analysis of a startup scheme for modular multilevel converters［J］.IEEE Transactions on Industrial Electronics，2015，62（11）：7009-7024.

［16］YU Feng，LIN Weixing，WANG Xitian，etal.Fastvoltagebalancing control and fast numerical simulation model for the modular multilevel converter［J］.IEEE Transactions on Power Delivery，2015，30（1）：220-228.

［17］MESHRAM P M，BORGHATE V B.A simplified nearest level control voltage balancing method for modular multilevel converter［J］.IEEE Transactions on Power Electronics，2015，30（1）：450-462.

［18］HUANG Ming，ZOU Jianlong，MA Xikui.An improved phaseshifted carrier modulation for modular multilevel converter to suppress the influence of fluctuation of capacitor voltage ［J］.IEEE Transactionson PowerElectronics，2016，31（10）：7404-7416.