中间再热式汽轮发电机组的多指标非线性鲁棒综合控制

陈明媛 ，李啸骢 ，从兰美 ，2，徐俊华 ，任子熠

（1.广西大学 广西电力系统最优化与节能技术重点实验室，广西 南宁 530004；2.临沂大学 汽车学院，山东 临沂 276005）

0 引言

由于大功率中间再热式汽轮发电机组在电力系统中已得到普遍应用，因此研究其控制对于提高电力系统的稳定性起着重要的作用，备受广大学者们的关注［1-3］。

文献［4］引入多指标非线性控制设计方法研究中间再热式汽轮发电机组的高、中压缸汽阀和励磁系统的综合控制问题。该方法既能够使系统获得良好的动态性能，也能够使其获得满意的静态性能。文献［5］应用目标全息反馈法处理中间再热式汽轮发电机组的非线性综合控制。该方法可以将非线性控制系统的多个控制目标均约束在性能指标中，从而实现系统的多目标控制。然而，文献［4-5］建立的中间再热式汽轮发电机组模型均没有考虑系统参数的不确定性以及干扰的影响。为了提高非线性控制设计方法的有效性，使设计所得的控制律在实际应用中能够达到满意的控制效果，在系统建模和控制器的设计过程中考虑不确定性对系统的影响是必不可少的。

文献［6］讨论了中间再热式发电机的高压缸汽阀和励磁系统的鲁棒综合控制问题，但没有考虑中压缸汽阀和中间再热器的动态过程。文献［7］讨论了高压缸汽阀的鲁棒调速控制问题，但未涉及励磁和中压缸汽阀。文献［8］研究了高、中压缸汽阀的鲁棒控制问题，但没有考虑励磁控制。由此可见，大部分文献在对中间再热式发电机组进行鲁棒控制设计时，都对其数学模型进行了简化处理。

本文在不简化模型的情况下，探讨多机环境下的中间再热式汽轮发电机组的非线性鲁棒综合设计问题。笔者在文献［9］中提出了一种多指标非线性鲁棒控制设计方法（MINRCA）。由于MINRCA并不需要将原被控系统模型完全精确线性化，因此无需对被控对象的数学模型进行简化处理。应用MINRCA所获得的控制器不仅能使系统状态变量满足给定的性能指标，而且能有效提高系统对于不确定干扰因素的鲁棒性。

1 中间再热式发电机组励磁与调速系统的鲁棒综合控制数学模型

考虑一个具有n台中间再热式汽轮发电机的多机电力系统，以第i台发电机为例，其控制系统的结构如图1所示。

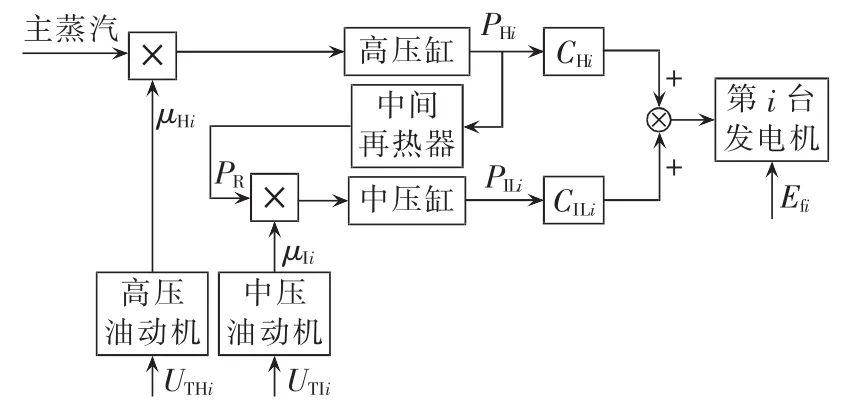
图1 控制系统结构图Fig.1 Structure of control system

根据图1可看出，第i台中间再热式汽轮发电机励磁与高、中压缸汽阀的鲁棒综合控制数学模型可以表示如下：

其中，下标i=1，2，…，n为第i台发电机对应的状态量；w1i为作用在励磁回路中的电磁扰动；w2i为作用在高压缸调节阀的外部干扰；w3i为作用在中压缸调节阀的外部干扰。其他状态量的物理意义可参考文献［10-11］。w1i、w2i和 w3i均属于扩展 L2空间。属于扩展L2空间的信号在时间区间［0，T］上的定积分是有界的，其中p 为信号 w（t） 的维数［12］。

2 多指标非线性鲁棒综合控制规律的设计

对于如式（1）所示的系统，进行鲁棒综合控制的目标是：当扰动［w1i，w2i，w3i］T=0 时，系统是稳定的；当扰动 ［w1i，w2i，w3i］T≠0 时，扰动对系统输出的影响被抑制在给定水平。运用文献［9］提出的MINRCA，可设计出令系统满足上述控制目标的控制规律。

2.1 输出函数的选取

系统输出函数的选取，其参考依据如下［13］。

a.与励磁控制规律相关的输出函数y1i：励磁控制的目标之一是将发电机端电压保持在给定值，所以端电压偏差信号ΔUti=Uti-Ut0i，必须引入输出函数中进行约束，其中Ut0i为电压给定值；同时，发电机运行的稳定性也是一个重要的性能指标，因此转子角速度偏差Δωi=ωi-1也需引入输出函数中进行约束。

b.与高压缸汽阀开度控制规律相关的输出函数y2i：为实现对发电机转速的精确控制，发电机的转速偏差Δωi应引入输出函数中。汽门开度控制在并联运行的发电机中有实现有功功率合理调节和分配的作用，因此发电机的有功功率偏差值ΔPei也应纳入输出函数中。为了使油动机环节有较好的调节性能，油动机的汽阀开度ΔμHi=μHi-μH0i也需引入输出函数中，其中μH0i为高压缸汽阀开度的给定值。

c.与中压缸汽阀开度控制规律相关的输出函数y3i：控制中压缸汽阀开度的目的与高压缸相似，因此选入输出函数y3i的系统变量与选入输出函数y2i的相似。但是，由于调节高压缸会引起中间再热器的输出功率发生变化，因此中压缸汽阀开度的控制还应能进一步反映中间再热器的输出功率的变化，故ΔPRi=PRi-PR0i信号也要引入输出函数中，其中PR0i为中间再热器输出功率的给定值。

2.2 系统的动态扩展

为消除系统的有功运行点发生改变后，电磁功率Pei出现的稳态偏差，本文借鉴文献［4］的动态扩展方法，定义一个新的系统状态变量，则式（1）所示系统可扩展为如下仿射非线性系统：

根据2.1节中所提的输出函数选取依据并结合动态扩展，则式（5）所示系统的输出函数为：

其中，ΔμIi=μIi-μI0i，μI0i为中压缸汽阀开度的给定值；ΔPeil=Peil-Pe0il。

2.3 控制规律的设计

令扰动［w1i，w2i，w3i］T=0，输出函数对系统的相对阶可由式（12）确定［14］。

易知，矩阵（x）是非奇异的。那么，系统对于输出函数的相对阶为r=3n。显然相对阶r小于系统的总阶数9n。因此，形如式（11）所示的输出函数仅能将系统部分精确线性化。

为系统的前3n个方程选择非线性变换坐标如下：

为系统的后6n个方程选择非线性变换坐标如下：

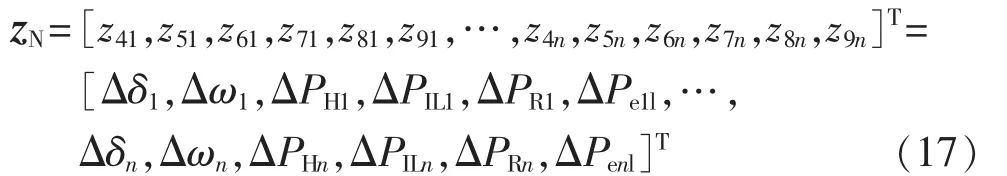
显然，非线性变换坐标式（17）满足：

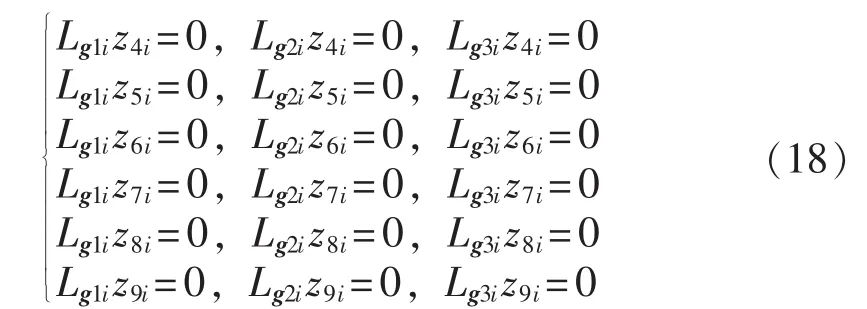
在非线性坐标变换式（16）和（17）的作用下，系统可以转化成如下的形式：

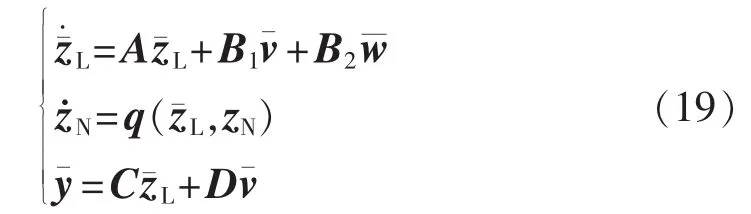
假设CTD=0，且DTD是可逆的。

将线性子系统L的二次性能指标选取为：

若对于如下 Riccati方程［15］：

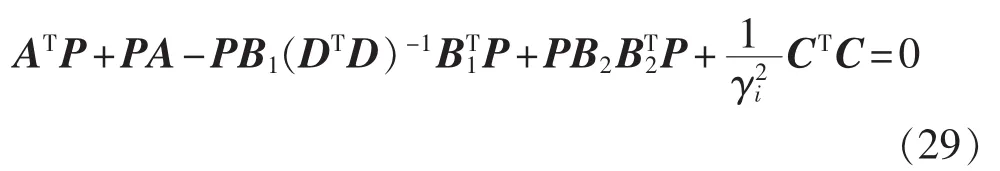
在控制规律的作用下，线性子系统L的闭环系统在x=0处是渐进稳定的，并且干扰输入到调节输出的 L2增益小于 γi。

线性子系统L的鲁棒控制规律如下所示：

其中，K= （DTD）-1，k（s）×（s）（s=1，2，…，3n）为矩阵K的第s个对角线元素。将式（31）和（32）代入式（25），将控制规律从z空间变换回x空间，得到鲁棒励磁控制规律Efi、鲁棒汽阀开度控制规律UTHi及UTIi。

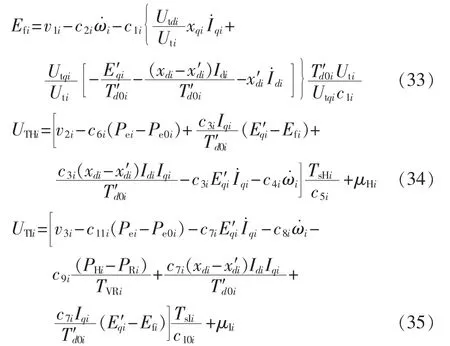
从式（33）—（35）可以看出，第i台发电机的鲁棒励磁控制规律Efi、汽门开度控制规律UTHi及UTIi仅包含该台发电机相关的状态变量，因此所求出的控制规律是具有分散性的。

当线性子系统进入稳定状态时，有L=0。将L=0代入式（19），那么系统的零动态可重写成：

由于输出函数中的待定系数c1i、c2i、c3i、c4i、c5i、c7i、c8i和c9i出现在零动态系统中，那么通过适当地赋值，可以调节零动态系统的稳定性。

3 系统仿真结果

第2节中所设计的多指标非线性鲁棒综合控制方法的有效性将在如图2所示的三机电力系统中进行验证。

图2 三机电力系统示意图Fig.2 Diagram of three-machine power system

图2中发电机G1是无穷大系统，G2和G3装配有综合控制器，其模型参数如表1 所示［16］。表中，x′di、xdi、xqi为标幺值。

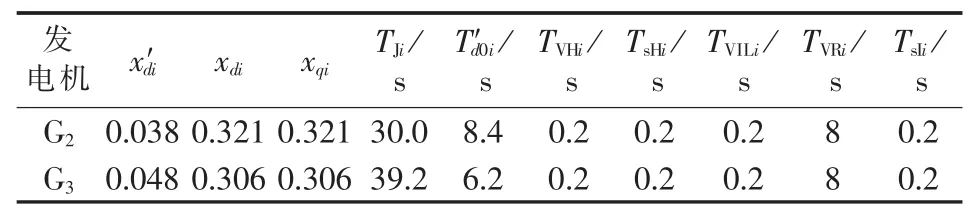
表1 发电机G2和G3的模型参数Table 1 Parameters of G2and G3

在实际应用中，由于发电机的容量有限，所以仅能提供有限的励磁电压。因此，励磁电压和汽阀开度的物理极限如下：

3.1 控制规律参数的选取

在MINRCA中，参数γi越小，说明干扰抑制效果越好。然而，太小的γi会导致Riccati方程无解。所以，应该选择适当的参数γi。在方程式（29）中，令γi=0.1（i=2，3），且令：

求解Riccati方程，可得：

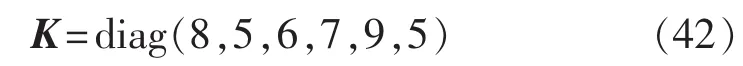
如式（11）所示的输出函数的代数参数选取为：

将式（42）和（43）代入控制规律式（33）—（35），得到的控制规律代入系统方程式（5），那么闭环系统的一次渐进系统的特征根配置在如式（44）所示的位置。

3.2 零动态系统的稳定性

在控制规律式（33）—（35）的作用下，零动态系统的特征根配置在如下的位置：

显然，零动态系统的特征根都位于负半平面，可见零动态系统是稳定的。

3.3 仿真案例与仿真结果

为验证多指标非线性鲁棒综合控制律（MINRC）的有效性，针对下述4种扰动方案，将其与多指标非线性综合控制律（MINC）进行仿真对比。

MINC指将输出函数选取为如式（11）所示的形式，输出函数的代数参数选取同式（43），二次性能指标中参数矩阵C和D的选取同式（40）和（41），求解式（46）所示的 Riccati方程［17］，可得式（47）。

将式（43）和（47）代入式（33）—（35），可得MINC。

3.3.1 电压调节扰动

在0.5 s时刻，G2的机端电压给定值阶跃调高2.5%，同时G3的机端电压给定值降低2.5%。系统在MINRC、MINC的作用下，各状态变量的响应曲线分别见图3、图4。图中 Ut、Pe、ω 为标幺值，后同。

图3和图4表明，当经历电压调节扰动时，发电机的机端电压在MINRC、MINC的作用下均能按调节要求对给定值进行跟踪，发电机输出的有功功率未因为出现调压扰动而出现偏差；发电机的功角及角速度的响应特性十分平滑，没有发生振荡现象。

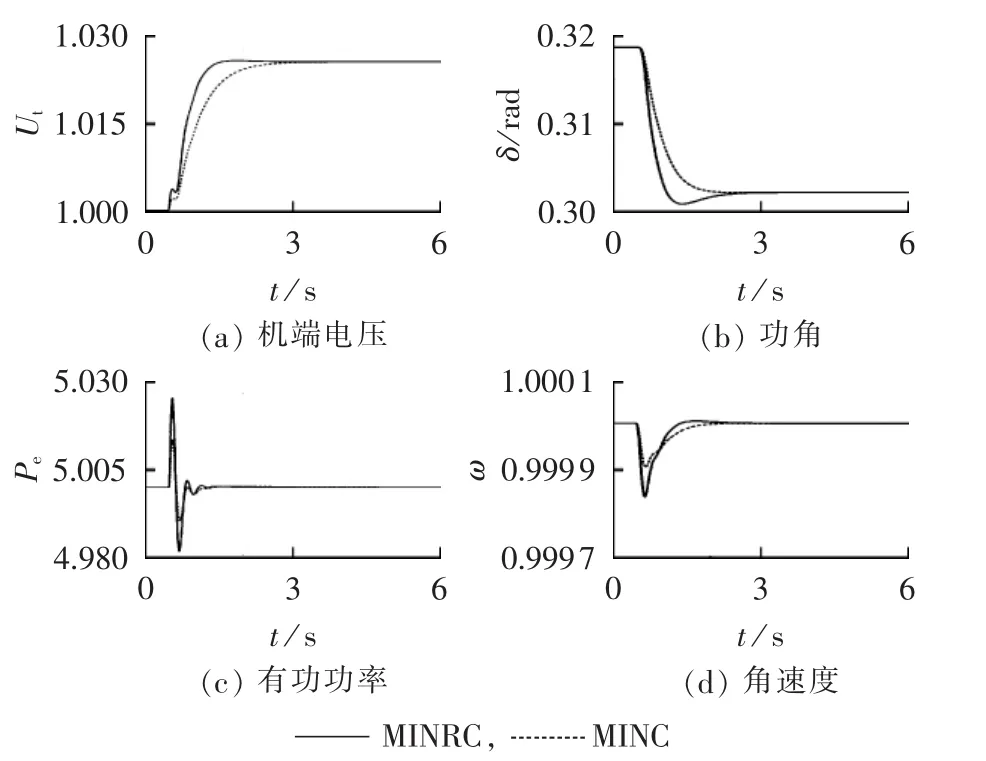
图3 电压调节扰动时发电机G2的系统响应曲线Fig.3 System responses for G2under voltage regulation disturbance

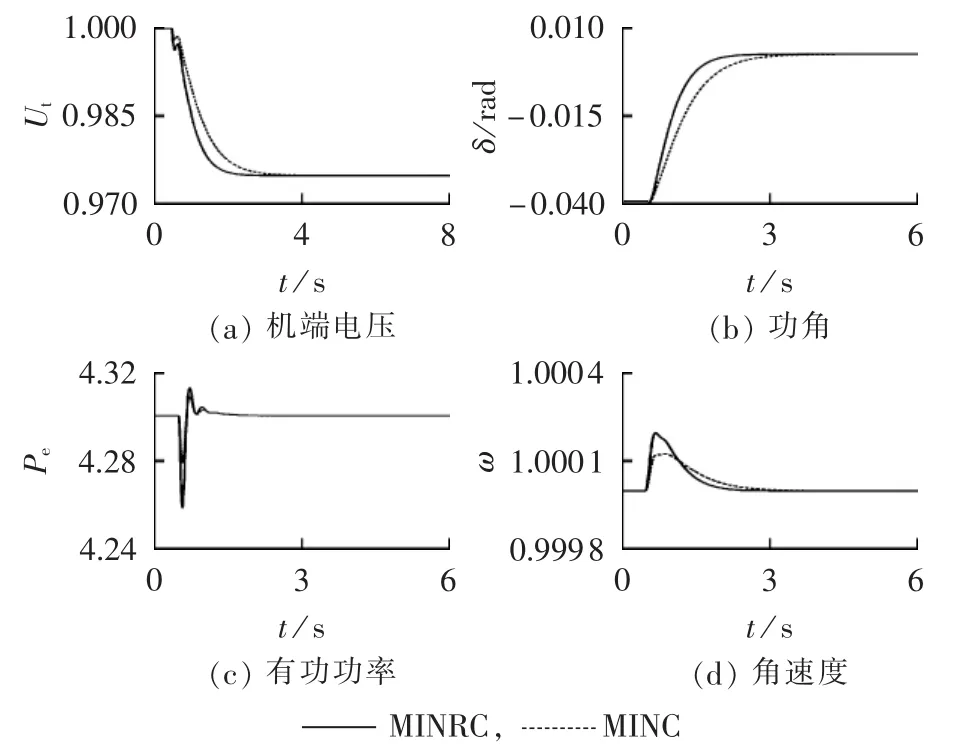
图4 电压调节扰动时发电机G3的系统响应曲线Fig.4 System responses for G3under voltageregulation disturbance

3.3.2 有功调节扰动

在0.5s时刻，发电机G2输出的有功功率从5 p.u.变为5.5 p.u.，同时发电机G3输出的有功功率从4.3 p.u.变为 4 p.u.。系统在MINRC、MINC的作用下，各状态变量响应曲线分别如图5和图6所示。

由图5和图6可知，在MINRC、MINC的作用下，发电机输出的有功功率均能按调节要求准确跟踪给定值，机端电压在经过小波动后，恢复到初始运行点而不会产生静态偏移；发电机G3功角减小以适应机械功率输入的减小，发电机G2功角增大以适应机械功率输入的增加，这些特性与实际相符。

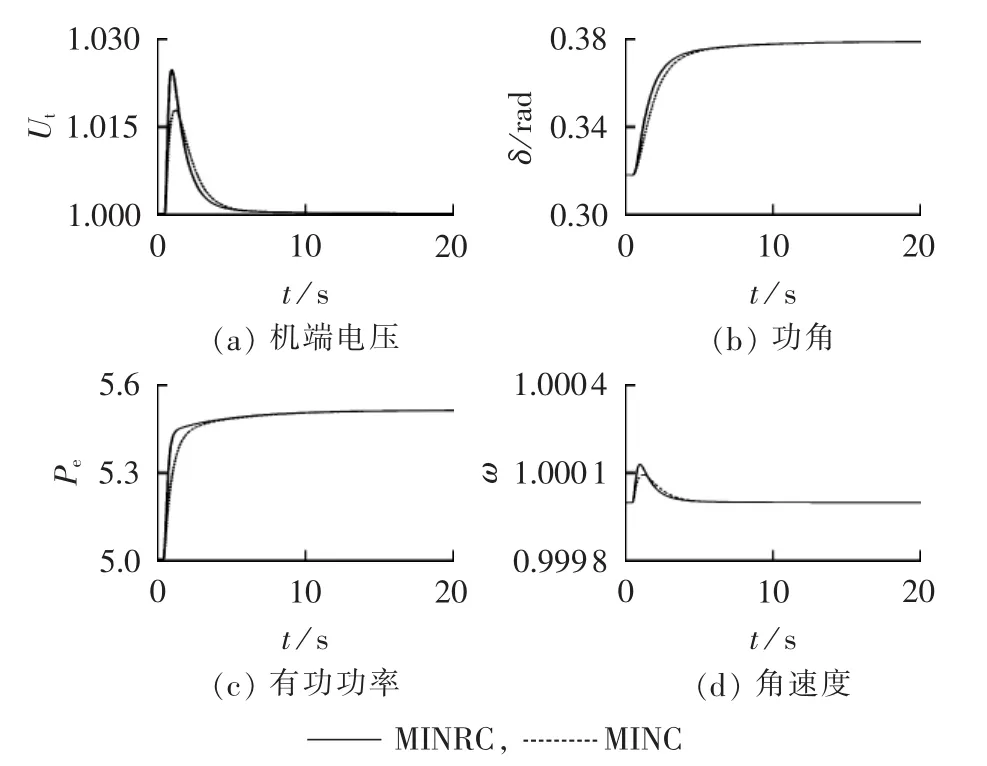
图5 有功功率调节扰动时发电机G2的系统响应曲线Fig.5 System responses for G2under active power regulation disturbance

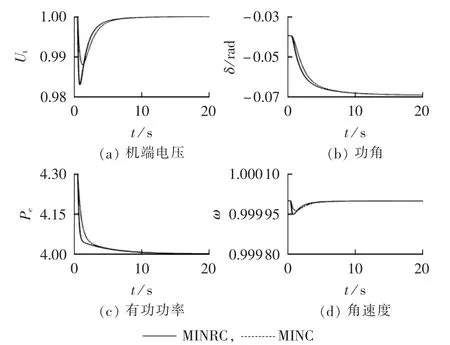
图6 有功功率调节扰动时发电机G3的系统响应曲线Fig.6 System responses for G3under active power regulation disturbance

图3—6表明，在MINRC、MINC作用下的系统响应具有较为相似的特性，都能提高中间再热式汽轮发电机组的动态性能，并在进入稳态后均能保证相关状态量准确跟踪给定值，具有令人满意的静态性能。

3.3.3 外部扰动

在0.5 s时刻，系统受到外部干扰。作用在发电机 G2、G3的干扰分别为 w12=w22=w32=sin t、w13=w23=w33=-sin t。系统在MINRC、MINC的作用下，有关状态量的响应曲线分别如图7和图8所示。

图7和图8表明，当发电机受到外部干扰时，其机端电压、功角、发电机输出的有功功率都不同程度地发生了偏移，说明发电机的运行状态发生了改变。但相比之下，在MINRC作用下产生的静态偏移比在MINC要小得多，可见MINRC比MINC具有更加有效的干扰抑制作用，能使系统具有较好的鲁棒性。

图7 外部扰动时发电机G2的系统响应曲线Fig.7 System responses for G2under exogenous disturbance

图8 外部扰动时发电机G3的系统响应曲线Fig.8 System responses for G3under exogenous disturbance

3.3.4 三相短路扰动

在扰动发生前，系统处于稳定状态。在0.5 s时刻，5号和8号母线之间的线路（靠近5号母线端处）发生三相金属性短路，故障持续0.15 s后被切除，0.8 s时系统重合闸成功。当系统采用MINRC、MINC时，系统有关状态量的响应曲线分别见图9和图10。

图9 三相短路扰动时发电机G2的系统响应曲线Fig.9 System responses for G2under three-phase short circuit fault

图10 三相短路扰动时发电机G3的系统响应曲线Fig.10 System responses for G3under three-phase short circuit fault

图9、图10表明，当系统发生大扰动时，在MINRC、MINC作用下，机端电压均能很快地恢复到初始状态，且有效地平息了有功功率的摆动并抑制了系统的超调，使得发电机具有良好的暂态稳定性能。

4 结语

本文针对一个具有n台中间再热式汽轮发电机的多机电力系统，建立其鲁棒综合控制模型。运用MINRCA，成功设计出多机环境下的中间再热式汽轮发电机组励磁与高、中压缸汽阀的MINRC。仿真结果表明，MINRC能维持发电机端电压在给定值上运行，准确控制发电机的转速，合理调节和分配发电机的有功，提高发电机运行的稳定性，实现了系统的多目标控制；同时，MINRC综合控制律相比于MINC能更有效地抑制扰动对系统输出的不利影响，增强了系统的鲁棒性。

参考文献：

［1］黎浩荣，李东海，李立勤，等.中间再热式汽轮发电机组汽门开度全程非线性控制［J］.清华大学学报（自然科学版），2000，40（10）：84-87.LI Haorong，LI Donghai，LI Liqin，et al.Reheat-type turbogenerator steam valve whole range non-linear control［J］.Journal of Tsinghua University（Natural Science Edition），2000，40（10）：84-87.

［2］刘辉，汪旎，韦化，等.发电机组目标全息反馈大范围稳定控制设计［J］.中国电机工程学报，2009，29（31）：21-26.LIU Hui，WANG Ni，WEI Hua，et al.Global asymptotic stable coordinated control with objective holographic feedbacks for the turbo-generator set［J］.Proceedings of the CSEE，2009，29（31）：21-26.

［3］CHEN H，JI H B，WANG B，et al.Coordinated passivation techniques for the dual-excited and steam-valving control of synchronous generators［J］.IEE Proceedings－Control Theory and Applications，2006，153（1）：69-73.

［4］李啸骢，程时杰，韦化，等.中间再热式汽轮发电机组的多指标非线性综合控制器的研究［J］.电网技术，2004，28（7）：1-6.LI Xiaocong，CHENG Shijie，WEI Hua，et al.Study on multiindex nonlinear integrated controller for reheat-type turbogenerator unit［J］.Power System Technology，2004，28（7）：1-6.

［5］刘辉，韦化，李啸骢.大型汽轮发电机组目标全息反馈非线性综合控制设计［J］.电工技术学报，2008，23（4）：25-31.LIU Hui，WEI Hua，LI Xiaocong.Nonlinear coordinated control with objective holographic feedbacks for large turbogenerator set［J］.Transactions of China Electrotechnical Society，2008，23（4）：25-31.

［6］王冰，季海波，陈欢，等.汽轮发电机励磁与汽门协调无源性控制［J］.中国电机工程学报，2004，24（5）：104-109.WANG Bing，JIHaibo，CHEN Huan，etal.The coordinated passivity techniques for the excitation and steam-valving control of generator［J］.Proceedings of the CSEE，2004，24（5）：104-109.

［7］刘鑫蕊，孙秋野，谢志远，等.基于观测器的多机系统气门开度的模糊H∞控制新方法［J］.东北大学学报（自然科学版），2015，36（12）：1678-1681.LIU Xinrui，SUN Qiuye，XIE Zhiyuan，et al.New observer-based fuzzy H∞control approach for steam valve opening of multimachine power systems［J］.Journal of Northeastern University（Natural Science Edition），2015，36（12）：1678-1681.

［8］JIANG N，LIU T，LI S，et al.Whole-range nonlinear large disturbance attenuation controller design for turbo generator steam valve systems［J］.Journal of Dynamic Systems Measurement&Control，2013，136（1）：81-89.

［9］LI Xiaocong，CHEN Mingyuan，LIANG Zhijian，et al.Excitation and steam-valving coordinated robust controller design for multimachine powersystemsbased on the multi-index nonlinear robust control approach［J］.IEEJ Transactions on Electrical&Electronic Engineering，2016，11（4）：425-434.

［10］LU Q，SUN Y，XU Z.Decentralized nonlinear optimal excitation control［J］.IEEE Transactions on Power Systems，1996，11（4）：1957-1962.

［11］JIN M J，HU W，LIU F，et al.Nonlinear coordinated control of excitation and governor for hydraulic power plants［J］.IET Proceedings－Generation，Transmission and Distribution，2005，152（4）：544-548

［12］卢强，梅生伟，孙元章.电力系统非线性控制［M］.北京：清华大学出版社，2008：182-183.

［13］李啸骢，郑涛，梁志坚，等.水轮机水门、励磁与电气制动系统非线性综合控制［J］.电力自动化设备，2016，36（7）：97-103.LIXiaocong，ZHENG Tao，LIANG Zhijiang，etal.Integrated nonlinear control of hydroturbine governor and excitation and TCBR system［J］.Electric Power Automation Equipment，2016，36（7）：97-103.

［14］潘月斗，郭凯，陈继义，等.基于状态反馈线性化的矩阵变换器非线性控制［J］.电力自动化设备，2015，35（5）：77-82.PAN Yuedou，GUO Kai，CHEN Jiyi，et al.Nonlinear control of matrix converter based on state feedback linearization［J］.Electric Power Automation Equipment，2015，35（5）：77-82.

［15］李啸骢，程时杰，韦化，等.具有多性能指标的汽轮发电机非线性综合控制［J］.中国电机工程学报，2003，23（4）：96-101.LI Xiaocong，CHENG Shijie，WEI Hua，et al.Multi-index nonlinear integrated control for turbine generator unit［J］.Proceedings of the CSEE，2003，23（4）：96-101.

［16］LU Q，SUN Y.Nonlinear stabilizing control of multi-machine systems［J］.IEEE Transactions on Power Systems，1989，4（1）：236-241.

［17］MEI S，LIU F，CHEN Y.Coordinated H∞control of excitation and governor of hydroturbo-generator sets：a Hamiltonian approach［J］.International Journal of Robust and Nonlinear Control，2004，14（9-10）：807-832.