基于戴维南-诺顿等效的含分布式光伏发电系统的配电网仿真分析

黑晨阳，关远鹏，谢运祥，朱曦萌

（1.华南理工大学 电力学院，广东 广州 510640；2.华中科技大学 强电磁工程与新技术国家重点实验室，湖北 武汉 430074）

0 引言

能源与气候是当前最为重要的议题之一。化石能源的大量使用使得气候变暖，且其存储量急剧减少，严重威胁到了人类的生存。可再生能源作为当前最为合适的解决方案，正在快速发展［1］。光伏发电系统是可再生能源在电力系统中的重要应用方式之一［2-3］，在覆盖率和装机容量上快速发展，并受到国内外学者的广泛研究。目前，我国城市中的建筑物屋顶光伏分布式发电系统已成为最主要的实现形式之一，已在各大城市的工业园区实现示范工程应用。据统计，2015年我国分布式光伏装机容量已达6060 MW。

电压暂降是电力系统中最为常见的故障之一［4］，每年对居民、商业及工业生产，尤其是敏感电力用户造成巨大的经济损失。在分布式光伏发电系统中，光伏并网逆变器作为可插拔式的光伏发电系统接口，将会直接受到电压暂降所带来的冲击，对光伏电池和分布式光伏发电系统的出力特性都会造成影响，主要表现在光伏的P-V曲线和工作电压都会发生变化，不利于电力系统的稳定运行［5］。

目前，对含有分布式发电系统的配电网建模与仿真研究，主要有详细模型［6］和平均值模型［7-10］。详细模型是基于电力电子设备中的开关器件的控制建立的，能够准确地对分布式发电系统的控制方案、输出特性进行建模与仿真。但分布式发电系统的详细模型计算量比较大，在暂态过程仿真中会造成仿真平台溢出，不利于实际的仿真分析。

分布式发电系统的平均值模型主要关注发电模块以及接口的出力特性，在很大程度上简化了接口设备的内部具体开关模块环节，贴近详细模型的输出精度。而且分布式发电系统的平均值模型可以选择在较大步长下进行仿真，加快配电网电力系统的仿真速度。目前，已有大量学者对此进行研究分析。

针对含有分布式光伏发电系统的配电网系统或微电网，文献［6，11-12］对分布式光伏发电系统建立了平均值模型，并与详细模型进行仿真对比，在一定步长的仿真下，两者暂态过程的出力特性具有良好的一致性，然而，所建立的暂态模型中主要考虑了分布式发电单元，如光伏发电单元、风电发电单元和柴油机等模块，并没有考虑负荷的特性，不利于整个配电系统的稳定性研究。文献［13］将微电网中的负荷模型，如包含旋转电机和恒阻抗负荷的综合负荷，及分布式发电系统进行了化简，并在电压跌落扰动时分析各模块相应的出力特性，但将分布式光伏发电系统等效为功率因数为1的电流源，这与其在暂态过程中的控制方案，尤其是低电压穿越的控制方案的建模不相符。文献［14-15］将综合负荷的出力特性映射到分布式光伏发电系统的P-V平面上，分析在电压暂降发生后配电系统的稳定性，但该模型对于无功的出力则没有相关的分析。文献［16］建立了简化的配电网模型，并对分布式光伏发电系统建立戴维南等效模型，但该模型主要讨论的是稳态工况下的电能质量问题，并未涉及暂态过程的控制和等效。文献［17］对光伏阵列和光伏并网逆变器的出力特性和控制算法进行线性化处理，并建立了考虑发电效率的平均值等效模型，但该模型仍旧没有考虑负荷的出力特性，对电网、负荷和分布式光伏发电系统三体的相互作用并没有进一步的研究。文献［18-19］考虑电压暂降发生的位置和概率以及电压跌落程度、电压跌落时间和故障形式，进行电压暂降下含有分布式光伏发电系统的可靠性评估和分析，该方法统一分析了电网、负荷和分布式光伏发电系统三体的相互作用，但是没有对各模块在电压暂降发生后的出力特性进行分析。文献［20］对分布式光伏发电系统进行小信号建模，分析其工作的稳态临界条件，但该模型并没有考虑负荷以及光伏并网逆变器在低电压穿越时的出力特性。而文献［21］建立了分布式光伏发电系统的静态模型，并考虑了负荷的多样性。文献［22］则考虑在负荷发生突变时分布式光伏发电系统的频域稳定性。文献［23］则采用序分量分解的方法对故障状态下的分布式光伏发电系统进行分析，但并未给出分布式光伏发电系统的等效电源模型。

本文所提出的分布式光伏发电系统的戴维南-诺顿等效模型，介于详细模型和平均值模型之间。首先，对分布式光伏发电系统建立了在控制模型下的戴维南-诺顿等效模型，并充分考虑了光伏发电模块的P-V曲线以及光伏并网逆变器的低电压穿越控制方案。同时，对光伏分布式发电系统中的负荷，如非线性设备及包含旋转电机和恒阻抗负荷的综合负荷进行简化推导，获得相应的出力特性的戴维南-诺顿等效模型。考虑电压暂降过程，对所建立的戴维南-诺顿等效模型与详细模型进行印证。

1 含分布式光伏发电系统的配电网系统

1.1 系统的构成

含有分布式光伏发电系统的配电网如图1所示。分布式光伏发电系统向电网发送由太阳能所转换的电能，与大电网同时为用户负荷提供电能。配电网中的用户负荷，可通过提取典型负荷进行简化分析和研究，典型负荷主要有：

a.旋转电机负荷，主要是异步电机，包括空调、水泵等，随着生活的改善，该类负荷增长迅速；

b.恒阻抗负荷，主要是对电压暂降不敏感的负荷；

c.非线性负荷，随着电力电子设备的大量接入，该类负荷的增长更为迅猛，其非线性特性给配电网的稳定运行带来许多不确定的因素。

图1 含分布式光伏发电系统的配电网Fig.1 Distribution network with distributed photovoltaic generation system

由于配电网的线路接线比较复杂，在进行简化分析时特别要考虑线路和变压器的阻抗。

1.2 分布式光伏发电系统

分布式光伏发电系统主要包括光伏阵列和光伏并网逆变器以及相应的控制系统，如图2所示。光伏阵列的输出功率受光照强度以及工作电压点的影响较大，因此通常采用最大功率点跟踪（MPPT）算法来保证光伏阵列处于最大功率点处。并通过Boost电路稳定直流侧的输出电压。逆变器将光伏阵列的直流输出转化为交流电，实现分布式光伏发电系统并网。其控制策略一般采用的是双闭环控制。但为了在电网故障下快速提供无功支持，除了传统的电压闭环外，增加了无功功率的虚闭环，以支持电网快速恢复，提高电网的稳定性。

图2 分布式光伏发电系统Fig.2 Distributed photovoltaic generation system

在电压暂降发生时，故障将直接作用在逆变器上，虽然逆变器上存在直流侧电压闭环控制，但直流侧电压仍存在波动，会影响光伏阵列的工作状态，使得光伏阵列的P-V曲线在故障下发生变化，进而影响逆变器的输出特性。

通常大中型并网逆变器都具备低电压穿越能力，使其在电压暂降过程中能保持并网运行，减小电力系统的故障振荡，促进故障恢复。在现行光伏并网逆变器的并网要求中，并非要求逆变器在电压暂降下一直保持并网，当公共连接点PCC（Point of Common Coupling）电压在图3中的电压轮廓之上时，并网逆变器保持并网，反之，并网逆变器可以随时脱网。图中电压为标幺值。

图3 并网逆变器低电压穿越能力要求Fig.3 Requirements for low voltage ride through capability of grid-connected inverter

2 等效模型

在含有分布式光伏发电系统的配电网仿真中，分布式光伏发电系统的模型及其简化的准确性对仿真的真实性和效率至关重要。目前，主要的仿真模型有详细模型和平均值模型，但主要存在以下问题。

a.基于电力电子器件工作模态的详细模型，虽然能够很真实地反映逆变器的工作状态和出力特性，但是在配电网的系统仿真中，节点的增加以及分布式光伏发电系统的控制环节导致系统仿真占用较大的内存，出现仿真溢出、速度慢和效率低等问题。

b.现有的文献［9-12］也提出了相关的分布式发电系统的平均值模型，但更多的是关注考虑用户负荷时该模型的稳态特性，以及该模型在暂态时的设备出力特性，而缺少考虑模型在暂态时的出力特性和真实性，以及基于电力电子器件的非线性负荷的出力特性。

本节对光伏并网逆变器的控制算法深入分析，具体考虑光伏阵列的出力特性，对模型进行相应的简化；并分析在负荷为非线性负荷旋转电机和恒阻抗负荷的情况下，分布式光伏发电系统的暂态输出特性。

2.1 分布式光伏发电系统等效模型

在图2所示的分布式光伏发电系统中，化简后的光伏并网逆变器的电流反馈控制如图4所示。采用电力电子开关管的平均值模型，KPWM为调制波到逆变器的输出函数：

图4 分布式光伏发电系统的电流控制方案Fig.4 Current control strategy of distributed photovoltaic generation system

图中，Idqref、Udq、ICdq、UCdq、USdq和 ISdq分别为并网逆变器电流参考值矩阵、并网逆变器交流侧输出电压矩阵、并网逆变器LCL滤波器电容电流矩阵、并网逆变器LCL滤波器电容电压矩阵、并网电压矩阵和并网电流矩阵，即：

根据图4，上述各变量存在如式（3）所示的约束关系。

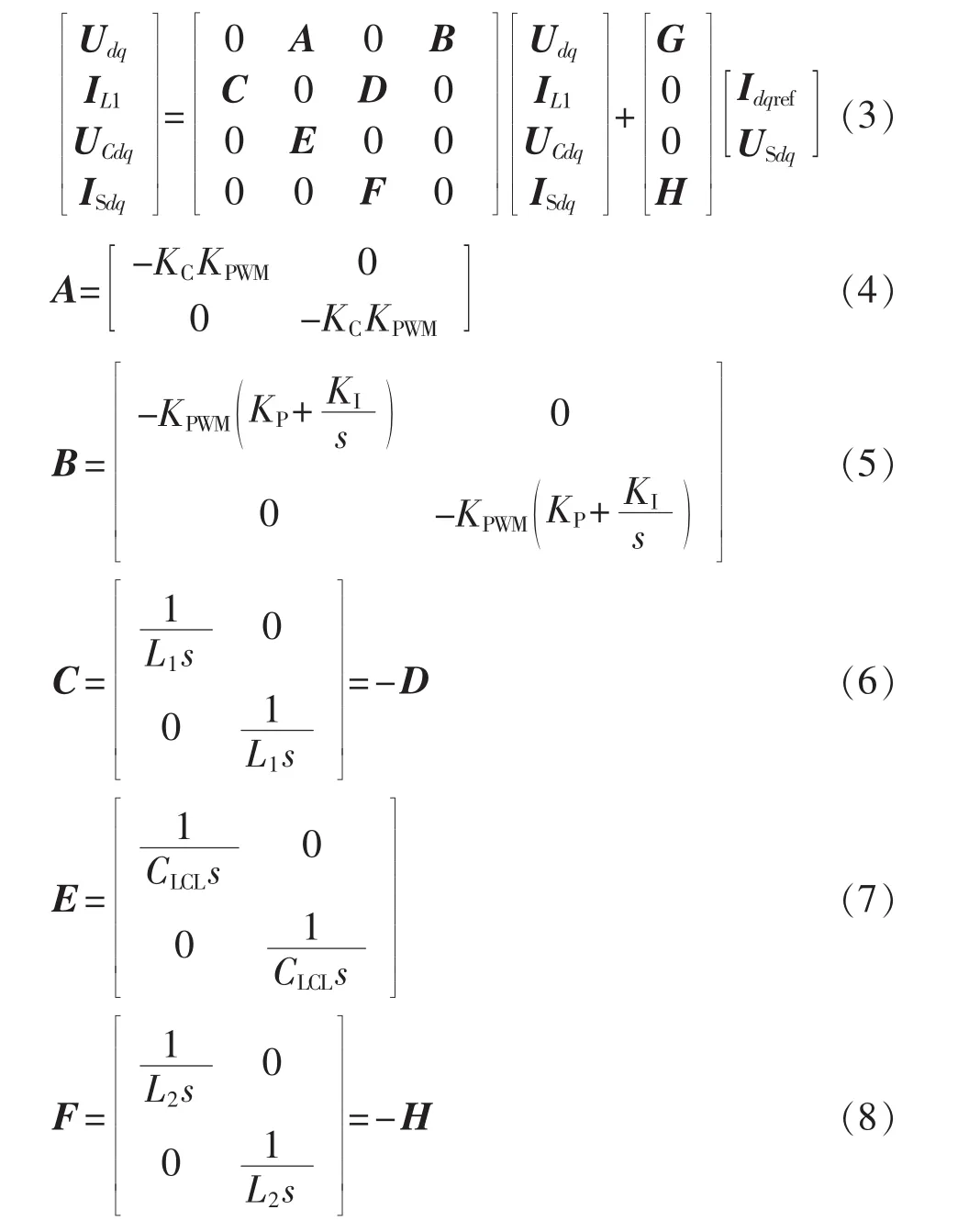
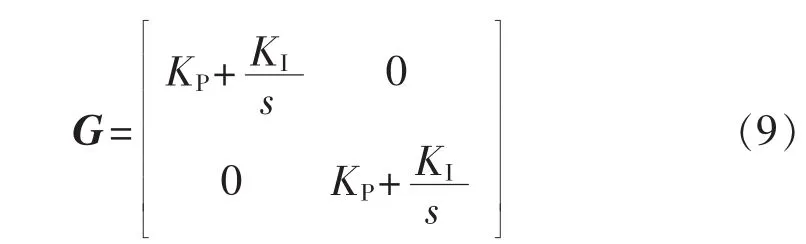
其中，KC为LCL滤波器电容电流反馈参数；KP、KI为PI控制器参数。

将式（3）化简后，可获得输出电流与参考电流和并网电压之间的关系，并建立分布式光伏发电系统的戴维南-诺顿等效模型，如图5（d）和式（10）—（12）所示。

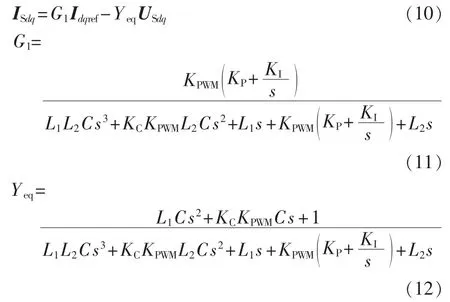
其中，G1Idqref为戴维南-诺顿等效模型中的等效电流源；Yeq为等效导纳。

逆变器的单桥臂戴维南-诺顿硬件等效过程如图5所示。桥臂上的开关阻值由开关管的开关状态决定，直流侧模块则等效为理想电源串联电阻。因此，可采用图5（b）所示的电路对图5（a）电路进行化简，其中，二极管的作用是防止直流侧电压为负值。进一步化简可获得图5（c）和图5（d）所示的简化电路。图5（d）中的电流源等效在考虑控制方式时，相应的电流值由式（10）—（12）决定。该等效过程表明，硬件简化模型与控制方案简化模型具有一致性。

图5 逆变器单桥臂戴维南-诺顿等效过程Fig.5 Thevenin-Norton equivalent process for single bridge arm of inverter

在电压暂降的过程中，分布式光伏发电系统不脱网运行，并向电网提供适当的电压支撑，有利于促进电网的故障恢复，即实现光伏并网逆变器的低电压穿越。光伏并网逆变器的低电压穿越控制策略通过对电压暂降时公共连接点的无功功率和并网电压的检测，在并网逆变器的最大功率范围的约束下，给定参考电流值，使其快速向电网发出无功支撑电流。该环节可以等效为一个无功功率闭环环节，见图6。

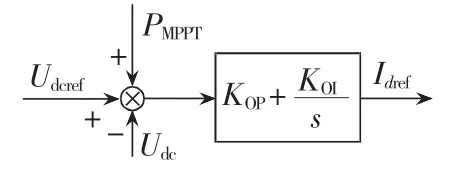
图6 d轴参考电流的给定Fig.6 Preset d axis reference current

与此同时，直流电压环依旧工作，稳定直流侧电压，可有效地降低输出电流的总谐波含量，见图7。但由于电压暂降的作用，在光伏阵列的P-V曲线中，最大功率点和相对应的电压将发生变化，如图8所示，图中功率、电压均为标幺值。这将使电压外环的光伏功率发生变化，光伏逆变器的输出有功功率降低，严重影响光伏并网逆变器的输出特性。

图7 q轴参考电流的给定Fig.7 Preset q axis reference current

图8 故障发生时P-V曲线变化Fig.8 Change of P-V curve after fault

因此，d轴和q轴的参考电流的整定分别为：

其中，为外环控制器；PMPPT为光伏阵列输出的最大功率。

2.2 综合负荷等效模型

在配电网中，旋转电机作为负荷占有很大的比重。一般工业上使用的旋转电机为异步电机。而异步电机在电压暂降过程中，机械的转速和转矩出力及电磁的暂态出力特性受端口电压的影响较大。因此，异步电机的暂态过程需要分析其电磁暂态过程和机械暂态过程。

图9（a）为异步电机的机械暂态过程等值电路。该电路主要考虑异步电机的功率特性，很大程度上忽略了电磁暂态过程。图9（b）为异步电机的电磁暂态过程和机械暂态过程的等值电路，该电路计及转子回路的电磁暂态过程和机械暂态过程，其中次暂态电动势E″LD和修正系数K分别由式（15）和（16）给定。

其中，PLDM0-jQLDM0为异步电机初始工作时的功率，可由铭牌以及初始工作时的潮流进行辨识；XLD=x1+xm，为定子开路时转子的时间常数，x1、x2、xm分别为异步电动机定子漏电抗、转子漏电抗和励磁电抗。

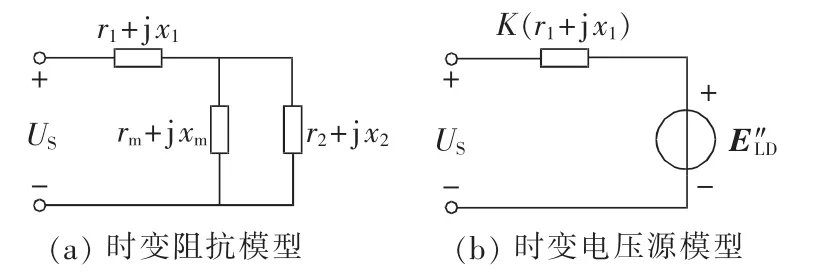
图9 异步电机等效模型Fig.9 Equivalent model of asynchronous motor

在电压暂降过程发生后，异步电机的转速将发生变化，使得转矩减小，即有功功率的输出将减小，而此时异步电机吸收的无功功率将增加。这会使异步电机转速增加甚至失稳，或在阻尼转矩的作用下异步电机迅速停止工作，如图10所示（图中转矩、转速均为标幺值）。

图10 异步电机机械特性Fig.10 Mechanic characteristics of asynchronous motor

在电力系统中，负荷除异步电机外，还存在一些其他的负荷，如照明、加热、制冷等用户负荷。这些负荷对电压暂降并不敏感，可以考虑采用恒定阻抗或导纳来表示，其值可以通过正常工作时的视在功率对其进行辨识，如式（17）所示。本文采用阻抗模型，ZLD为恒定阻抗，RLD和X′LD分别为其中的等效电阻和等效电抗，US为电网电压，SLD为负载的视在功率。

2.3 非线性负荷等效模型

基于电力电子开关器件的非线性负荷在配电网中广泛接入，给电网的稳定运行带来不确定因素，如图11所示。与光伏并网逆变器差异较大的是基于电力电子开关器件的非线性负荷的控制方案。该非线性负荷主要是整流器以及变频器，很少考虑到故障穿越。通常，该非线性负荷的控制方案，主要保证与电网相连一级的模块能够使该负荷的功率因数接近1，具有较为稳定的直流侧电压，而且没有输出最大功率点的限制，但存在容量的限制。因此，在建立模型时，应注意：

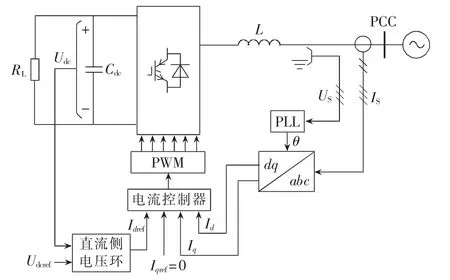
图11 非线性负荷电网侧模型Fig.11 Power grid side model of nonlinear load

a.电流控制器的输出存在饱和；

b.d轴的参考电流可以由电压外环确定，q轴的参考电流则为0。

由此构建基于控制模块的电力电子非线性负荷的等效模型。本文采用的是多阶等效系统，充分考虑控制环节中的暂态过程以及控制时延，如图12所示。图中，SIC为电流内环的等效传递函数；为电压环的采样延迟；0.75mcosθ为一时变环节，与PWM的矢量控制和开关函数的基本相位角相关；为直流侧电容和负载的等效阻抗。

图12 非线性负荷控制环节Fig.12 Control segment of nonlinear load

由图12可得基于控制环节的非线性负荷的等效模型，如图13所示。

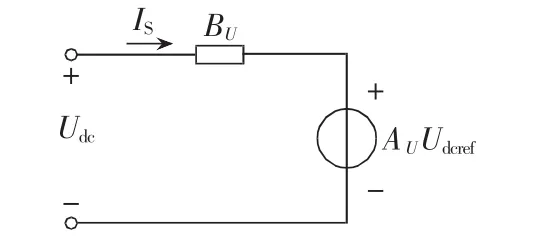
图13 非线性负荷等效模型Fig.13 Equivalent model of nonlinear load

3 算例分析

本文选用IEEE 13节点配电系统，并对其进行改造，在节点634和节点675分别加入额定容量为400 kW的分布式光伏发电系统。节点646和611的负荷替换为基于电力电子开关器件的非线性负荷，其余负荷节点改造为包含电机负荷和恒阻抗负荷的综合负荷，如图14所示。具体仿真参数见表1—4。

图14 改进的IEEE 13节点配电系统Fig.14 Improved IEEE 13-bus distribution system

表1 仿真节点数据Table 1 Node data of simulation

表2 分布式光伏发电系统仿真参数Table 2 Simulation parameters of distributed photovoltaic generation system

表3 综合负荷仿真参数Table 3 Simulation parameters of synthetic load

表4 非线性负荷仿真参数Table 4 Simulation parameters of nonlinear load

在节点650外，1.4 s时配电网发生三相短路故障，故障传至节点632时，体现为电压暂降故障，节点电压跌落深度为75%的额定电压值，持续时间为0.1 s。本文以节点634、652、646作为功率动态特性的观测点，分别对应分布式光伏发电系统、综合负荷和非线性负荷的功率动态特性，如图15—17所示。

图15 分布式光伏发电系统（节点634）功率动态特性Fig.15 Dynamic power characteristics of distributed photovoltaic generation system（Node 634）

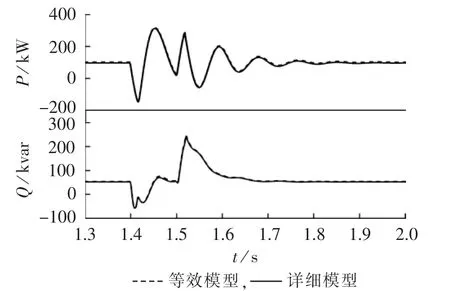
图16 综合负荷（节点652）功率动态特性Fig.16 Dynamic power characteristics of synthetic load（Node 652）

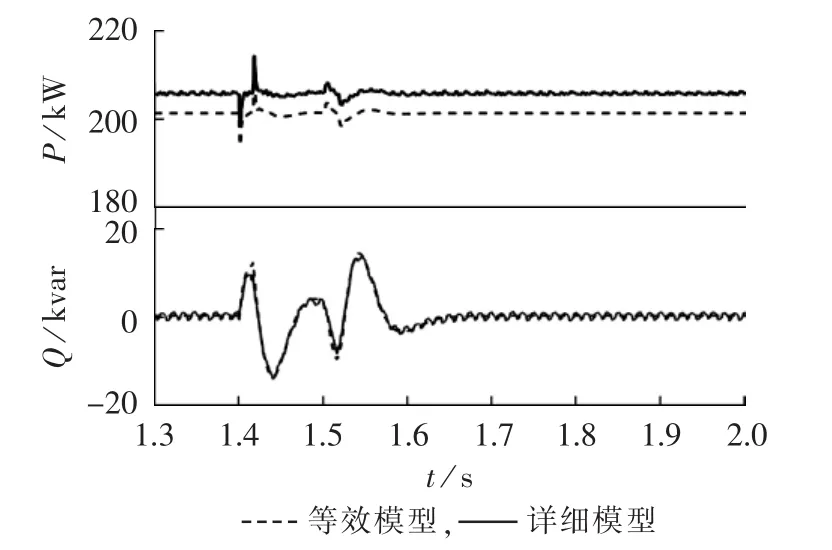
图17 非线性负荷（节点646）功率动态特性Fig.17 Dynamic power characteristics of nonlinear load（Node 646）

在图15中，分布式光伏发电系统等效模型和详细模型的动态无功功率特性存在一定的偏差，但是整个动态过程的变化趋势是相同的；两者的动态有功功率特性几乎完全吻合。图16所示的综合负荷的等效模型和详细模型的动态功率特性完全吻合。图17所示的非线性负荷等效模型和详细模型的动态有功功率特性存在整体性的偏差，但是变化的过程具有一致性；且在动态无功功率特性中，等效模型的曲线比较平滑，详细模型的曲线存在较大的纹波，但两者仍保持着高度的一致性。可见，等效模型与详细模型总体等效，能够完全反映整体系统的动态特性。

4 结论

分布式光伏发电系统等效模型的建立是提高其仿真速度的有效手段。本文对分布式光伏发电系统和非线性负荷的主要模块和相应的一般性控制方案进行等效简化。对包含旋转电机和恒阻抗负荷的综合负荷，本文建立旋转电机的转子动态等效电势模型。通过以上3种主要负荷模型的简化，本文建立了具有一般形式的戴维南-诺顿等效负荷模型。最后，在改进的IEEE 13节点配电系统下，通过对相关用户的节点动态功率进行观测，并与详细模型的结果进行对比，验证了所建立的等效模型在含有分布式光伏发电系统的配电网系统中的正确性和有效性，有效地降低了仿真运行时间占用的内存空间，并且仿真的输出具有较高的准确性。

参考文献：

［1］陈炜，艾欣，吴涛，等.光伏并网发电系统对电网的影响研究综述［J］.电力自动化设备，2013，33（2）：26-32.CHEN Wei，AI Xin，WU Tao，et al.Influence of grid-connected photovoltaic system on power network ［J］.Electric Power Automation Equipment，2013，33（2）：26-32.

［2］郭镥，罗安，黎燕，等.新型光伏逆变器及其前馈功率预测控制［J］.电力自动化设备，2013，33（6）：119-123.GUO Lu，LUO An，LI Yan，et al.New photovoltaic inverter and its feedforward power predictive control［J］.Electric Power Automation Equipment，2013，33（6）：119-123.

［3］李斌，袁越.光伏并网发电对保护及重合闸的影响与对策［J］.电力自动化设备，2013，33（4）：12-17.LI Bin，YUAN Yue.Impact of gridconnected photovoltaic power generation on protection and reclose，and itscountermeasures［J］.Electric Power Automation Equipment，2013，33（4）：12-17.

［4］刘旭娜，肖先勇，汪颖.电压暂降严重程度及其测度、不确定性评估方法［J］.中国电机工程学报，2014，34（4）：644-658.LIU Xuna，XIAO Xianyong，WANG Ying.Voltage sag severity and its measure and uncertainty evaluation［J］.Proceedings of the CSEE，2014，34（4）：644-658.

［5］谭骞，徐永海，黄浩，等.不对称电压暂降情况下光伏逆变器输出电流峰值的控制策略［J］.电网技术，2015，39（3）：601-608.TAN Qian，XU Yonghai，HUANG Hao，et al.A control strategy for peak output current of PV inverter under unbalanced voltage sags［J］.Power System Technology，2015，39（3）：601-608.

［6］王成山，高菲，李鹏，等.电力电子装置典型模型的适应性分析［J］.电力系统自动化，2012，36（6）：63-68.WANG Chengshan，GAO Fei，LI Peng，et al.Adaptability analysis of typical power electronic devicemodels［J］.Automation of Electric Power Systems，2012，36（6）：63-68.

［7］许寅，陈颖，陈来军，等.PWM 变流器分段平均模型中的纹波估计方法［J］.电网技术，2013，37（8）：2143-2150.XU Yin，CHEN Ying，CHEN Laijun，et al.A ripple estimation method for piecewise averaged model of PWM converters［J］.Power System Technology，2013，37（8）：2143-2150.

［8］许寅，陈颖，陈来军，等.基于平均化理论的PWM变流器电磁暂态快速仿真方法（一）PWM变流器分段平均模型的建立［J］.电力系统自动化，2013，37（11）：58-64.XU Yin，CHEN Ying，CHEN Laijun，et al.Fast electromagnetic transientsimulation method forPWM converters based on averaging theory part one establishment of piecewise averaged model for PWM converters［J］.Automation of Electric Power Systems，2013，37（11）：58-64.

［9］许寅，陈颖，陈来军，等.基于平均化理论的PWM变流器电磁暂态快速仿真方法（二）适用PWM变流器分段平均模型的改进EMTP 算法［J］.电力系统自动化，2013，37（12）：51-56.XU Yin，CHEN Ying，CHEN Laijun，et al.Fast electromagnetic transientsimulation method forPWM converters based on averaging theory part two improved EMTP algorithm suitable for piecewise averaged model of PWM converters［J］.Automation of Electric Power Systems，2013，37（12）：51-56.

［10］高海翔，陈颖，于智同，等.基于平均化理论的PWM变流器电磁暂态快速仿真方法（三）适用于图像处理器的改进EMTP并行仿真算法［J］.电力系统自动化，2014，38（6）：43-48.GAO Haixiang，CHEN Ying，YU Zhitong，et al.Fast electromagnetic transient simulation method for PWM converters based on averaging theory part three improved EMTP parallel algorithm for graphic processing unit［J］.Automation of Electric Power Systems，2014，38（6）：43-48.

［11］郭力，王成山.含多种分布式电源的微网动态仿真［J］.电力系统自动化，2009，33（2）：82-86.GUO Li，WANG Chengshan.Dynamical simulation on microgrid with different types of distributed generations［J］.Automation of Electric Power Systems，2009，33（2）：82-86.

［12］艾欣，金鹏，韩晓男，等.基于平均值模型的微电网建模及仿真分析［J］.现代电力，2013，30（5）：1-6.AI Xin，JIN Peng，HAN Xiaonan，et al.Modeling and simulation of microgrid based on average model［J］.Modern Electric Power，2013，30（5）：1-6.

［13］曹相芹，鞠平，蔡昌春.微电网仿真分析与等效化简［J］.电力自动化设备，2011，31（5）：94-98.CAO Xiangqin，JU Ping，CAIChangchun.Simulativeanalysis and equivalentreduction formicro-grid ［J］.Electric Power Automation Equipment，2011，31（5）：94-98.

［14］KAWABE K，TANAKA K.Impactofdynamicbehaviorof photovoltaic powergeneration systemson short-term voltage stability［J］.IEEE Transactions on Power Systems，2015，30（6）：3416-3424.

［15］KAWABE K，TANAKA K.Analyticalmethodforshort-term voltage stability using the stability boundary in the P-V plane［J］.IEEE Transactions on Power Systems，2014，29 （6）：3041-3047.

［16］PATSALIDES M，EFTHYMIOU V，STAVROU A，et al.Simplified distribution grid model for power quality studies in the presence of photovoltaic generators ［J］.IET Renewable Power Generation，2015，9（6）：618-628.

［17］WEIXiaodong，EDWIN F，SPAGNUOLO G，etal.Efficient approaches formodeling and simulating photovoltaic power systems［J］.IEEE Journal of Photovoltaics，2013，3（1）：500-508.

［18］MARTIN D，LEMON S.Simplifiedmodelingoflow voltage distribution networks for PV voltage impact studies［J］.IEEE Transactions on Smart Grid，2016，7（4）：1924-1931.

［19］贾东梨，刘科研，盛万兴，等.有源配电网故障场景下的电压暂降仿真与评估方法研究［J］.中国电机工程学报，2016，36（5）：1279-1288.JIA Dongli，LIU Keyan，SHENG Wanxing，etal.Voltagesag simulation and evaluation in active distribution network with fault cases［J］.Proceedings of the CSEE，2016，36（5）：1279-1288.

［20］BUENO P，HERNÁNDEZ J，RUIZ-RODRIGUEZ F.Stability assessmentfortransmission systems with large utility-scale photovoltaic units［J］.IET Renewable Power Generation，2016，10（5）：584-597.

［21］SAMADI A，SÖDER L，SHAYESTEH E，et al.Static equivalent of distribution grids with high penetration of PV systems［J］.IEEE Transactions on Smart Grid，2015，6（4）：1763-1774.

［22］GOLPI^RA H，SEIFI H，HAGHIFAM M.Dynamic equivalencing of an active distribution network for large-scale power system frequency stability studies［J］.IET Generation，Transmission&Distribution，2015，9（15）：2245-2254.

［23］MIRSAEIDIS，SAID D，MUSTAFA M，etal.A protection strategy for micro-grids based on positive-sequence component［J］.IET Renewable Power Generation，2015，9（6）：600-609.