基于双解耦的配电网三相不平衡快速潮流算法

陈 醒 ，卫志农 ，沈海平 ，孙国强 ，臧海祥 ，孙永辉

（1.河海大学 能源与电气学院，江苏 南京 210098；2.国网无锡供电公司，江苏 无锡 214061）

0 引言

配电网潮流计算是进行配电网分析的基础。近年来，随着分布式电源DG（Distribution Generation）的大量接入及主动配电网技术的快速发展，传统配电网正在从“单源”模式向“多源”模式转变，系统的不对称性日益明显，网络结构更加复杂，因此传统的配电网潮流分析方法难以适应当前的配电网［1-6］。为了进一步提高当前配电网潮流的计算效率，增强算法的适应性，有必要寻找一种高效的配电网潮流快速算法。

近年来，国内外学者对配电网潮流算法进行了大量研究。文献［7-8］采用经典牛顿-拉夫逊方法建立了三相潮流模型，有效解决了配电网三相不平衡潮流计算，但是该算法模型复杂，每次需重新生成雅可比矩阵，耗时长。为进一步提高三相潮流计算的效率，文献［9-12］从序分量的角度出发，提出了基于序分量法的三相潮流计算方法。虽然该方法进行了三序解耦，提高了潮流计算的效率，但是其主要针对的是输电网的三相潮流计算。考虑到配电系统在拓扑结构和运行方式上与输电网有着明显区别，因此需要研究适用于配电网的三相潮流。

前推回代算法原理简单，能够适应辐射型配电网络，因此在配电网潮流计算中被广泛应用。文献［13］提出了辐射型网络潮流的分层前推回代算法，该算法将网络支路按层次进行分类，大幅提高了配电网潮流的计算速度。文献［14］提出一种基于道路矩阵的配电网三相潮流直接算法，该算法充分利用配电网络的结构特点，建立了节点电压与注入电流的关系矩阵，实现了潮流的快速计算，但是该算法处理环网的能力较弱。文献［15］提出了一种基于序分量的弱环配电网三相解耦潮流算法，该算法将序分量法和道路回路分析法相结合，具有一定的处理弱环网的能力。但由于配电线路参数的不对称性，序分量法解耦线路参数失效［16］，所以需要对解耦后的各序进行补偿，相序之间的多次变换增加了计算的复杂度。

作为经典牛顿法的改进算法，快速分解潮流算法凭借其收敛快、节省内存的优势在输电网潮流计算中获得了广泛应用，但由于配电网中线路高R/X比值的特点，快速分解算法无法直接应用于配电网。文献［17］提出的复数域标幺化（complex per unit normalization，简称cpu）技术，有效地解决了配电线路中高R/X比值的问题，进而将快速分解潮流算法成功地引入配电系统潮流计算中，但是该方法并未考虑配电网的三相不平衡问题。

结合现代配电系统中电源、线路、负荷三相不平衡以及环网现象，本文提出了一种相间解耦与复数域快速分解算法相结合的三相不对称配电网双解耦潮流快速算法。首先采用相间解耦补偿模型对配电线路三相进行解耦；然后利用复数域标幺化技术减小各相线路R/X比值的影响，继而引入快速分解潮流算法进行相内分解运算；最后利用IEEE 13、IEEE 34、IEEE 123标准测试系统对本文算法的收敛性、计算效率及其对含分布式电源以及弱环网的适应性进行了测试。

1 各类分布式电源的潮流计算模型

常用的分布式电源类型主要有PQ类型、PQ（V）类型和PV类型等［18］，本节以单相为例，简要介绍这些分布式电源的潮流计算模型。

1.1 PQ类型

此类型分布式电源发出的有功P、无功Q均为恒定值，其计算模型为：

其中，P、Q分别为节点有功、无功功率，参考方向以流出节点为正；Pg、Qg分别为给定的发电机有功、无功功率。

1.2 PQ（V）类型

此类型分布式电源的有功P恒定，无功Q与电压U有一定的函数关系，其计算模型为：

其中，U为节点电压幅值。

潮流计算中处理此类节点时，无功功率Q可以按照给定的函数关系求得，然后作为PQ节点处理。

1.3 PV类型

此类型分布式电源的有功P与电压U恒定，其计算模型为：

且满足：

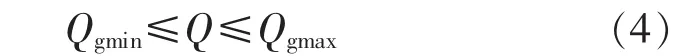
其中，Ug为给定的电压值；Qgmin、Qgmax分别为给定的无功下限与上限。在迭代过程中，如果发现该类型分布式电源的节点无功功率越限，则需要将其转换成对应的PQ节点。

当分布式电源以三相方式接入不平衡配电网时，由于配电网中三相电压不对称，分布式电源输出的三相功率并不相等，传统方法中近似认为分布式电源三相功率对称的处理方式就显得不够合理。针对此问题，本文拟采用文献［19-20］中考虑配电网不对称特性的分布式电源处理方式，在此不再赘述。

2 相间解耦模型

线路解耦补偿技术最早出现在文献［9］中，但其所提出的线路解耦补偿模型为序分量下的，借鉴文献［9］中的推导思路，可以推出相分量下的线路相间解耦补偿模型。

配电网线路的精确三相π型等值电路模型［21］如图1所示。

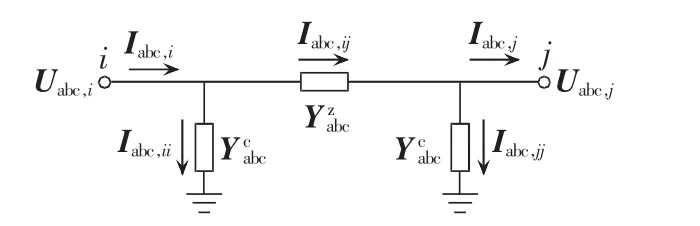
图1 配电线路三相π型等值电路模型Fig.1 Equivalent πtype circuit model of three-phase distribution line

图中，为线路的对地电容部分；为线路的导纳部分，那么线路的阻抗Zabc可以表示为：

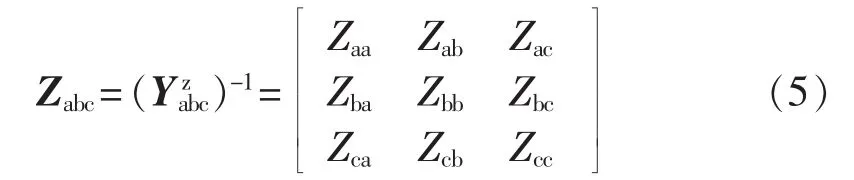
由图1可推导出解耦之前配电线路的导纳方程为：

考虑到配电网三相线路参数的不对称性，即三相相间互阻抗的不等性：

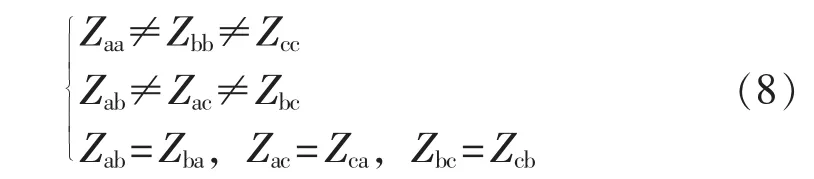
对式（6）直接进行展开，并将非对角线上的元素移到等式的右边，经整理后，进一步推导得：

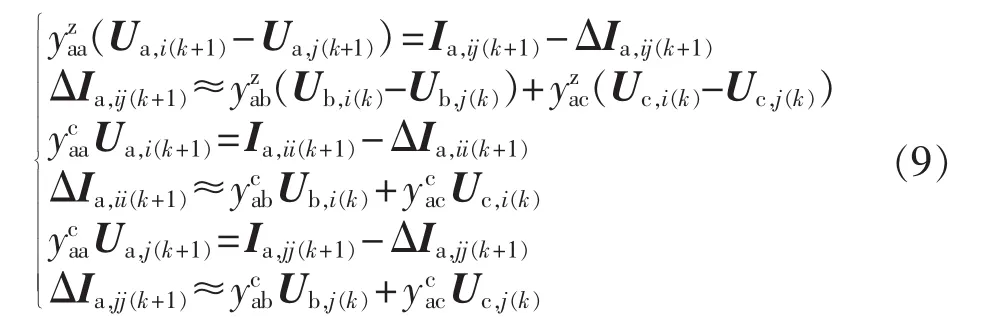
其中，k为迭代次数。

由式（9）可得到a相解耦补偿等效电路模型如图2所示。

图2 a相线路解耦补偿等效电路模型Fig.2 Decoupling compensation equivalent circuit model of phase-a line

根据a相解耦补偿电流等效电路模型，以流入节点方向为正，可以求出解耦后a相线路两端的节点注入补偿电流：

最后将解耦后a相线路两端的节点注入补偿电流，转化成相应的补偿注入功率加入线路两端节点注入功率中，完成第一步相间解耦工作：

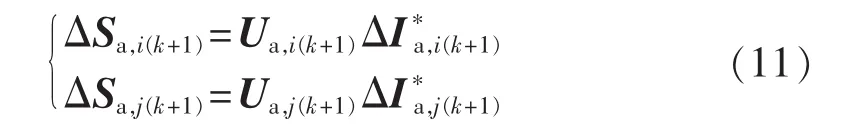
其中，上标*表示共轭。

同理，a相的解耦补偿模型可以类推到b相和c相，在此不再赘述。采用第一步的相间解耦模型之后，abc三相之间的耦合相应地转换成各相的补偿电流，从而实现了不对称三相线路的相间解耦，对于配电网三相潮流的计算则可以相应地转化成各相的计算，加快计算效率。

3 相内解耦模型

本文拟采用输电网中PQ快速分解潮流技术进行相内解耦，由于配电网络中线路高R/X比值的影响，传统的快速分解潮流计算无法直接应用在配电网络中。而文献［17］中提出的复数域标幺化技术在一定程度上减轻了配电线路中高R/X比值的影响，使得PQ快速分解潮流计算在配电网中的应用成为了可能。

3.1 复数域标幺化技术

传统的电力系统计算所采用的标幺化技术是在实数域上的标幺化，即在实数域上选定系统的功率基准值Sbase和电压基准值Ubase，计算相应的阻抗基准值Zbase，然后进行相应的标幺化。然而，复数域标幺化技术中的相应基准值则是在复数域下选取的。

在复数域下选定功率基准值、电压基准值为：

其中，φs为相应的功率基准角；φv为相应的电压基准角。

则求得相应的阻抗基准值为：

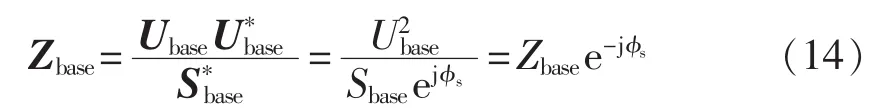
那么，在复数域下功率的标幺化形式为：

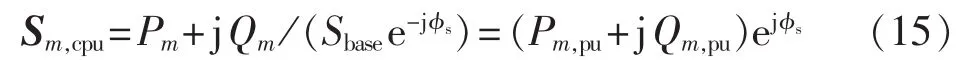
其中，m=1，2，…，t，t为注入功率数；下标 cpu 表示复数域下的标幺化；下标pu表示传统实数域下的标幺化。

在复数域下线路阻抗的标幺化形式为：

其中，i=1，2，…，l，l为支路数。

从式（16）可以看出，复数域下标幺化后的阻抗值与实数域下标幺化后的阻抗值相比，增加了一个功率基准角φs，这是复数域快速分解潮流可以在配电网中使用的一个至关重要的因素。

由传统输电网潮流计算的经验可知，线路参数R≪X是快速分解潮流计算的必要条件，也是传统输电网快速分解潮流算法很难适应配电网的重要原因，下文将详细介绍如何运用复数域标幺化的方法，解决配电线路中高R/X比值的问题。

由式（16）可知，复数域标幺化之后相应的电阻和电抗为：

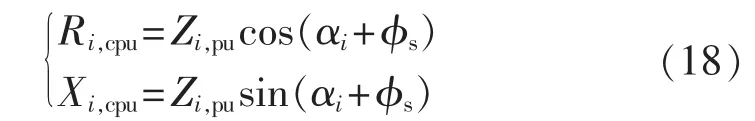
若要使得 Ri，cpu≪ Xi，cpu，则：

即有：

由式（20）知，αi是由线路固有参数决定的，因此可选定一个合适的功率基准角 φs使 αi+φs⇒π/2，从而使得 Ri，cpu≪ Xi，cpu，增强快速分解潮流算法在配电网络的适应性。由式（12）—（20）可以注意到，电压基准角 φv的选取并不影响 Ri，cpu≪ Xi，cpu，故本文取φv=0以减轻问题的复杂度，从而简化计算。

3.2 复数域功率基准角φs的选取

由3.1节可知，复数域功率基准角φs的选取对快速分解潮流算法在配电网络中的应用有决定性作用。相比文献［17］的复数域功率基准角φs的选取方案，本文基于最优化方法推导了φs的另一种选取方法。

由正切函数的性质可知：

由式（21）可知，当 αi+φs趋近于 π/2 的左侧时，tan（αi+φs）趋近于 +∞；当 αi+φs趋近于 π/2 的右侧时，tan（αi+φs）趋近于 -∞。分析可得，这 2 种趋近方式都能满足快速分解计算的要求，只是当选定的 φs使得部分线路的 tan（αi+φs）趋近于 -∞ 时，这些线路的R/X比值会出现负值的情况，这不符合线路参数所表现出的正常物理现象。故在复数域下选定功率基准角φs时，只是为了尽可能地减小R/X比值的影响，以增强快速分解潮流计算在配电网的适用性，复数域标幺化后的线路各参数并没有实际的物理意义。

本文采用优化的方法来选取功率基准角φs，首先建立如下目标函数：

根据式（22），函数 f（φs）表示所有线路的 αi移相φs之后，向左或向右靠近π/2的程度。所以求得使目标函数f（φs）值最小的φs即为要找的最优解。令 f（φs）对 φs的偏导为 0，即可求得 φs的最优解为：

相比于文献［17］中功率基准角φs的选取，本文从另一角度出发，建立了描述线路的αi移相φs之后与 π/2靠近程度的目标函数 f（φs），基于最优化原理确定了复数域功率基准角φs的最佳选择。在复数域下选定功率、电压基准值进行复数域标幺化之后，即可采用PQ快速分解法求解潮流，快速分解潮流算法在输电网领域已经发展的相当成熟，故在此不做详细的介绍。

4 配电网双解耦三相快速潮流计算

本文所介绍的配电网双解耦快速潮流计算整体思路如图3所示。

如图3所示，本文第一步采用相间解耦补偿模型在实数域标幺化下进行a、b、c相间解耦；第二步在复数域标幺化下将a、b、c各相进行PQ分解快速潮流计算；然后，反复迭代达到一定收敛精度之后，结束计算，返回潮流值。采用的收敛判据为a、b、c相的电压幅值与相角修正量绝对值的最大值。

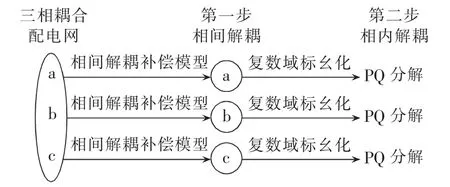
图3 双解耦潮流计算思路Fig.3 Calculation idea of double decoupling power flow

其中，ΔUa、Δθa、ΔUb、Δθb、ΔUc、Δθc分别为 a、b、c 相的电压幅值与相角的修正量；ε一般取值为10-6～10-4。

本文第一步相间解耦使用实数域标幺化和第二步相内解耦使用复数域标幺化主要有如下两方面的考虑。

其一，复数域标幺化的目的是降低配电网线路高R/X比值的影响，而第一步相间解耦模型与线路高R/X比值的相关性不大，所以第一步解耦无需复数域标幺化。

其二，在循环迭代计算时，第一步相间解耦补偿模型与第二步相内解耦模型所需交换的数据仅为各节点电压幅值和相角。在第2节介绍的复数域电压基准值的选取上，选取了电压基准角φv=0，从而使得Ubase=Ubase·ej0=Ubase，因此如果在实数域标幺化下电压基准值取Ubase，在复数域标幺化下电压基准值取Ubase·ej0，那么第一步相间解耦和第二步相内解耦中的电压数据可以直接进行交换，无需进行另外处理。

图4为三相不平衡配电网双解耦快速潮流计算方法流程图。

5 算例测试

本节从3个方面对本文提出的三相不对称配电网双解耦快速潮流计算方法展开了测试：第一，对该算法进行了收敛性与计算效率测试；第二，对本文中的选取方法与文献［17］中φs的选取方法进行了对比，并且展示了实数域标幺化和复数域标幺化后的线路参数变化情况；第三，对本文算法就分布式电源接入和弱环网的适应性进行了测试。程序采用MATLAB编程，在CPU为Intel 3.3 GHz 4核计算机上运行。

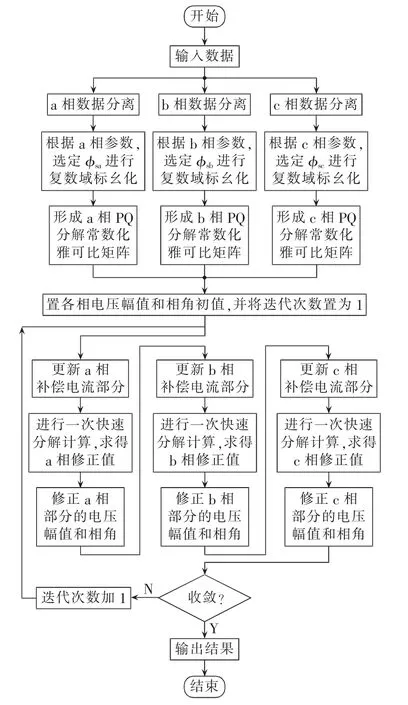
图4 三相不平衡配电网双解耦快速潮流计算流程图Fig.4 Flowchart of double decoupling power flow calculation for three-phase unbalanced distribution network

5.1 收敛性与计算效率测试

本文采用的算例测试系统为IEEE 13、IEEE 34、IEEE 123节点三相不平衡配电系统［22］，并选用3种方法进行了对比。为方便阐述，现规定：本文算法即相间解耦+复数域PQ分解法；方法1为传统三相牛顿潮流算法；方法2为相间解耦+单相牛顿法；方法3为相间解耦+实数域PQ分解法。本文算法与方法3的区别在于本文算法在第二步相内解耦过程中采用复数域PQ分解法，而方法3的第二步相内解耦过程则采用了实数域PQ分解法。

图5为IEEE 13节点三相不平衡系统的电压幅值（标幺值）计算结果，本文选择方法1计算结果作为本文算法计算结果的比较基准，收敛精度为10-5。从图5中可以看出，本文算法的计算结果与方法1的计算结果基本一致，验证了本文算法的有效性。

图5 IEEE 13节点系统的电压幅值Fig.5 Voltage amplitude of IEEE 13-bus system

图6为IEEE 34节点系统4种方法迭代次数与收敛精度的关系图，其中纵坐标表示的是收敛精度的负常用对数（-lg（·））。

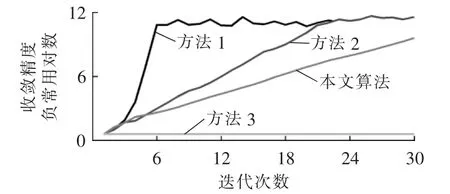
图6 IEEE 34节点系统4种方法迭代次数与收敛精度的关系图Fig.6 Relationship between iteration times and convergence accuracy of IEEE 34-bus system for four methods

从图6中可以看出，在IEEE 34节点测试系统中，作为经典潮流解法，方法1具有很好的收敛特性，经过5次迭代计算后，精度就能达到10-5。由于线路中高R/X比值线路的影响，方法3在该测试系统中不能有效收敛，验证了传统快速分解潮流算法在配电网潮流计算中适应性差的问题。本文算法和方法2具有相近的收敛特性，大都呈近似线性变化，其中方法2在10次左右计算精度能达到10-5，而本文算法在12次左右计算精度能达到10-5。可见，本文提出的算法具有一定的工程实用前景。

表1为4种方法在各测试系统中不同收敛精度下收敛次数的比较，收敛次数是不同收敛精度下每种方法运行100次的平均结果。从表1中可以看出，方法3在IEEE 13节点系统中可以收敛，但收敛效果不佳。由于配电线路参数高R/X比值的影响，方法3在IEEE 34节点系统和IEEE 123节点系统中均无法收敛。相比于方法3，本文算法在第二步相内解耦中采用复数域标幺化后，能够在其他测试系统中可靠收敛，并表现出与方法2相近的收敛次数。

由以上分析结果可知，本文算法相比方法1和方法2牺牲了部分收敛性，下面将结合计算耗时综合比较各方法的性能。图7为3种方法在IEEE 34、IEEE 123节点系统中平均计算时间的比较，收敛精度定为10-5，平均计算时间是每种方法运行100次的平均结果。

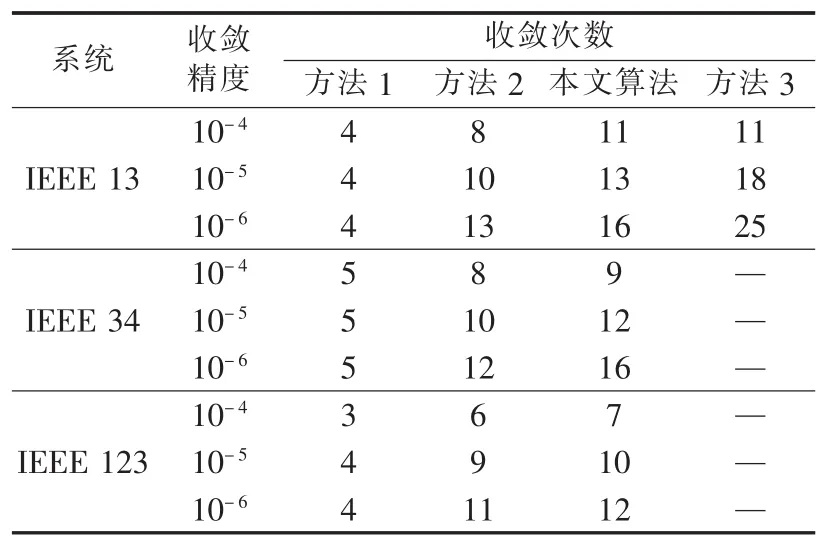
表1 各方法在不同收敛精度下收敛次数Table 1 Convergence times of each method for different convergence accuracies

图7 各方法的平均计算时间Fig.7 Average calculation time of each method

由图7可以看出，无论是IEEE 34节点系统，还是IEEE 123节点系统，本文算法的计算时间都明显小于方法1和方法2，且系统越大优势越明显。本文算法通过abc相间解耦、abc各相相内PQ解耦，大幅降低了雅可比矩阵的维度，减少了雅可比矩阵的存储空间；另外得益于雅可比矩阵的常数化，本文所提算法能有效节省计算时间，提高计算效率。结合表1和图7，虽然方法1的收敛性能优于本文算法，但是方法1在每次迭代求解和存储雅可比矩阵时消耗了大量时间，所以在工程实用角度上本文算法优于方法1。虽然本文算法在收敛性能上和方法2很相近，但是本文算法在计算效率上明显优于方法2。故综合来看，本文算法在计算性能上有着极大的优势，能实现三相不平衡配电网快速、高效的潮流计算。

5.2 功率基准角φs的选取方法对比

现将本文中复数域功率基准角φs的选取方法与文献［17］中所用方法进行比较。表2给出了在收敛精度为10-5时，这2种选取方法下φs的选取值与收敛次数。由表2可以看出，2种选取方法所选取的各相功率基准角φs有所不同，其中采用本文方法所选取的功率基准角在一定程度上减小了收敛次数，所以本文功率基准角φs选取方法相比于文献［17］的φs选取方法具有优越性。

表3展示了IEEE 34节点测试系统中复数域标幺化前后b相部分线路参数的变化情况。由表3可以看出，复数域标幺化之后线路值得到了一定程度的减小。部分线路参数出现了R值为负的现象，这种现象正好与本文第3.2节的分析结果一致，属于正常现象，复数域标幺化只是为了尽可能地减小线路R/X比值的影响，以增强快速分解潮流计算在配电网的适用性，复数域标幺化后的线路各参数并没有实际的物理意义。

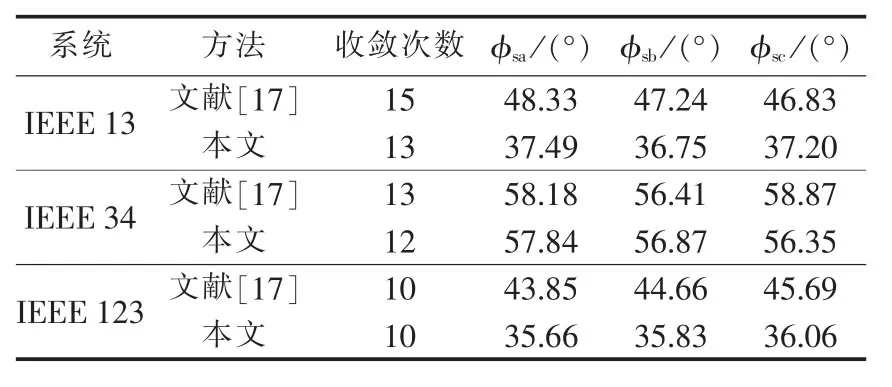
表2 2种功率基准角的选取方法Table 2 Two selection method of power base angles

表3 IEEE 34节点测试系统复数域标幺化后b相线路参数Table 3 Parameters of phase-b line after complex per unit normalization for IEEE 34-bus test system

5.3 分布式电源与弱环网的适应性测试

为测试本文所提双解耦快速潮流算法对分布式电源以及弱环网的适应性，本节在IEEE 34节点系统的基础上增加了几种常见的分布式电源以及联络线组成环网，并列举了几种接入方案进行测试。表4为各类型分布式电源接入参数，分布式电源接入参数配置可参考文献［18］，在处理abc三相接入的分布式电源时，本文所采取的处理方式认为该分布式电源对外输出的三相总功率保持恒定［19-20］。表5为联络线的接入参数，由于IEEE 34节点系统的地理接线架构未知，所以表5的联络线参数仅是为了达到环网效果而假定的试验值。为简单起见，所有的联络线路类型规定为300型［22］，接入方式均为abc三相接入。

表4 各分布式电源接入参数Table 4 Parameters of integrated DGs

表5 联络线的接入参数Table 5 Parameters of integrated contact-lines

图8为修改后的IEEE 34节点测试系统网络接线图，图中虚线表示联络线，由于分布式电源的接入和弱环网的出现，在一定程度上提高了系统的整体电压水平，故在修改后的IEEE 34节点测试系统中未考虑调压器部分。

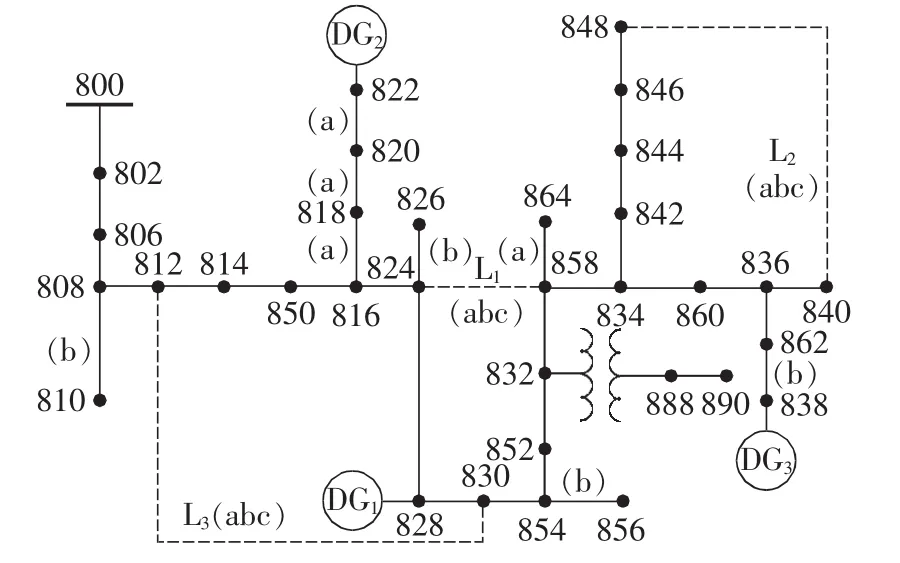
图8 修改后的IEEE 34节点测试系统Fig.8 Modified IEEE 34-bus test system

表6为5种接入方案下各方法迭代次数的比较，其中方法1和方法2是第5.1节中所用方法，此时的收敛精度为10-5。从方案1到方案5，方法1均能有效收敛，验证了传统牛顿法潮流计算在分布式电源和弱环网中的适应性。方法2在第一步相间解耦后依然用单相牛顿法求解潮流，所以在分布式电源和弱环网出现后仍具有稳定的收敛性。相比于方法1和方法2，本文算法在第一步相间解耦后采用复数域PQ分解法求解潮流，由于复数域PQ分解法本质为牛顿法的简化方法，故从方案1到方案5，在分布式电源接入种类和弱环网数量逐渐增多的情况下，本文算法亦表现出了稳定的收敛性。环网线路的出现改善了系统功率，减小了电压不平衡度［15］，本文算法的迭代次数有所减少，同时保持了其稳定的收敛性。

表6 5种方案下各方法的迭代次数Table 6 Iteration times of each method for five schemes

6 结论

本文提出了一种适应分布式电源和弱环网的三相不平衡主动配电网双解耦快速潮流算法。该算法有如下特点：第一步采用相间解耦补偿模型直接对三相不平衡配电网进行解耦，加快了潮流计算速度；第二步采用复数域标幺化技术削弱线路R/X比值的影响，基于PQ分解在各相进行快速分解潮流计算，进一步降低计算复杂度，并常数化雅可比矩阵，提高了潮流计算效率；相比文献［17］功率基准角φs的选取方法，本文的选取方法具有一定的优越性；相比于序分量解耦的方法，本文所提方法不需要相序之间的来回转换，计算操作更为简便；由于本文算法本质为简化的牛顿法，所以对分布式电源以及弱环网有着良好的适应性。

从算例分析的结果可以看出，本文算法的综合性能明显优于其他算法，具有计算高效、收敛线性、适应性强的特点。因此在三相不平衡配电网潮流计算的工程实用范围内，本文算法具有良好的应用价值。

参考文献：

［1］李鹏，窦鹏冲，李雨薇，等.微电网技术在主动配电网中的应用［J］.电力自动化设备，2015，35（4）：8-16.LI Peng，DOU Pengchong，LI Yuwei，et al.Application of microgrid technology in active distribution network［J］.Electric Power Automation Equipment，2015，35（4）：8-16.

［2］马钊，周孝信，尚宇炜，等.未来配电系统形态及发展趋势［J］.中国电机工程学报，2015，35（6）：1289-1298.MA Zhao，ZHOU Xiaoxin，SHANG Yuwei，et al.Form and development trend of future distribution system［J］.Proceedings of the CSEE，2015，35（6）：1289-1298.

［3］王建勋，吕群芳，刘会金，等.含分布式电源的配电网潮流快速直接算法［J］.电力自动化设备，2011，31（2）：17-21.WANG Jianxun，LÜ Qunfang，LIU Huijin，et al.Fast and direct power flow algorithm for distribution network with distributed generation［J］.Electric Power Automation Equipment，2011，31（2）：17-21.

［4］杨雄，卫志农，孙国强，等.含分布式电源的配电网三相解耦潮流计算方法［J］.电力自动化设备，2014，34（3）：99-107.YANG Xiong，WEIZhinong，SUN Guoqiang，etal.Decoupled three-phase power flow calculation for distribution network with DGs［J］.Electric Power Automation Equipment，2014，34（3）：99-107.

［5］赵波，王财胜，周金辉，等.主动配电网现状与未来发展［J］.电力系统自动化，2014，38（18）：125-135.ZHAO Bo，WANG Caisheng，ZHOU Jinhui，et al.Present and future development trend of active distribution network［J］.Automation of Electric Power Systems，2014，38（18）：125-135.

［6］张建华，曾博，张玉莹，等.主动配电网规划关键问题与研究展望［J］.电工技术学报，2014，29（2）：13-23.ZHANG Jianhua，ZENG Bo，ZHANG Yuying，et al.Key issues and research prospects of active distribution network planning［J］.Transactions of China Electrotechnical Society，2014，29（2）：13-23.

［7］ZHU Y，TOMSOVIC K.Adaptive power flow method for distribution systems with dispersed generation［J］.IEEE Power Engineering Review，2002，22（5）：72-72.

［8］王守相，黄丽娟，王成山，等.分布式发电系统的不平衡三相潮流计算［J］.电力自动化设备，2007，27（8）：11-15.WANG Shouxiang，HUANG Lijuan，WANG Chengshan，et al.Unbalanced three-phase power flow calculation for distributed power generation system［J］.Electric Power Automation Equipment，2007，27（8）：11-15.

［9］张小平，陈珩.不对称三相潮流的对称分量分析法［J］.中国电机工程学报，1993，13（6）：1-12.ZHANG Xiaoping，CHEN Heng.Unsymmetrical three phase load flow study based on symmetrical component theory［J］.Proceedings of the CSEE，1993，13（6）：1-12.

［10］ZHANG X P.Fast three phase load flow methods［J］.IEEE Transactions on Power Systems，1996，11（3）：1547-1554.

［11］ABDEL-AKHER M，NOR K M，RASHID A H A.Improved threephase power-flow methods using sequence components［J］.IEEE Transactions on Power Systems，2005，20（3）：1389-1397.

［12］黄少伟，陈颖，沈沉.不对称电力系统相序混合建模与三相潮流算法［J］.电力系统自动化，2011，35（14）：68-73.HUANG Shaowei，CHEN Ying，SHEN Chen.Hybrid modeling of asymmetrical power system and three-phase power flow method［J］.Automation of Electric Power Systems，2011，35（14）：68-73.

［13］颜伟，刘方，王官洁，等.辐射型网络潮流的分层前推回代算法［J］.中国电机工程学报，2003，23（8）：76-80.YAN Wei，LIU Fang，WANG Guanjie，etal.Layer-by-layer back/forward sweep method for radial distribution load flow［J］.Proceedings of the CSEE，2003，23（8）：76-80.

［14］李红伟，王敬章，张安安.一种含分布式发电系统的三相配电网潮流直接算法［J］.电力自动化设备，2012，32（1）：67-71.LI Hongwei，WANG Jingzhang，ZHANG Anan.Direct algorithm of three-phase power flow for radial distribution network with DGs［J］.Electric Power Automation Equipment，2012，32（1）：67-71.

［15］杨雄，卫志农，孙国强，等.基于序分量的弱环配电网三相解耦潮流算法［J］.中国电机工程学报，2014，34（7）：1167-1174.YANG Xiong，WEIZhinong，SUN Guoqiang，etal.A threephase decoupled power flow algorithm for weakly meshed distribution networks based on the sequence component［J］.Proceedings of the CSEE，2014，34（7）：1167-1174.

［16］姜彤，郭志忠，陈学允，等.多态相分量法及其在电力系统三相不对称分析中的应用［J］.中国电机工程学报，2002，22（5）：70-74.JIANG Tong，GUO Zhizhong，CHEN Xueyun，et al.Polymorphic phase components method and its application in three-phase unbalance calculation of power system［J］.Proceedings of the CSEE，2002，22（5）：70-74.

［17］TORTELLI O L，LOURENCO E M，GARCIA A V，et al.Fast decoupled powerflow toemergingdistribution systemsvia complex pu normalization［J］.IEEE Transactions on Power Systems，2015，30（3）：1351-1358.

［18］牛焕娜，井天军，李汉成，等.基于回路分析的含分布式电源配电网简化潮流计算［J］.电网技术，2013，37（4）：1033-1038.NIU Huanna，JING Tianjun，LI Hancheng，etal.Simplified power flow calculation for distribution network with distributed generation based on loop analysis［J］.Power System Technology，2013，37（4）：1033-1038.

［19］杨雄，卫志农，孙国强，等.主动配电网三相解耦潮流算法［J］.电工技术学报，2016，31（2）：186-195.YANG Xiong，WEI Zhinong，SUN Guoqiang，et al.Three-phase decoupled power flow algorithm for active distribution networks［J］.Transactions of China ElectrotechnicalSociety，2016，31（2）：186-195.

［20］王成山，孙充勃，彭克，等.微电网交直流混合潮流算法研究［J］.中国电机工程学报，2013，33（4）：8-15.WANG Chengshan，SUN Chongbo，PENG Ke，et al.Study on AC-DC hybrid power flow algorithm for microgrid［J］.Proceedings of the CSEE，2013，33（4）：8-15.

［21］王守相，王成山.现代配电系统分析［M］.北京：高等教育出版社，2007：11-13.

［22］Distribution System Analysis Subcommittee.Radial distribution test feeders［EB/OL］.（2011-02-01）［2015-09-23］.http：∥ewh.ieee.org/soc/pes/dsacom /testfeeders/index.html.