基于改进CPSO算法的区域电热综合能源系统经济调度

刘 洪 ，陈星屹 ，李吉峰 ，徐 科

（1.天津大学 智能电网教育部重点实验室，天津 300072；2.国网天津市电力公司，天津 300010）

0 引言

随着能源互联网的发展，多种能源在不同时间尺度上的相关性和互补性加深，如何调度综合能源系统 IES（Integrated Energy System）中各单元的出力以降低系统运行成本、提高能源利用率、减小环境污染，成为目前亟待解决的重要技术问题。在我国北方地区供热季，热电联产系统CHP（Combined Heating and Power system）通常在“以热定电”模式下工作，这种运行模式制约了机组出力的灵活性，不仅导致弃用大量风电，还增加了化石燃料的消耗。在区域电热综合能源系统中引入电储能ES（Electricity Storage）、热储能 HS（Heat Storage）、电动汽车 EV（Electric Vehicle）及电锅炉 EB（Electric Boiler）对电热进行联合调度，可更好地匹配可再生能源出力及电热负荷的峰谷特性。

目前针对多能系统经济运行和风电消纳的研究，多是以经济性和消纳弃风分别作为目标优化调度系统各单元出力。 文献［1］以包含风机WT（Wind Turbine）、光伏电池、热电联产系统、电锅炉、储热和储电等装置的并网型微电网为例，求得调度周期内系统最优总运行成本。文献［2］为实现微电网整体优化的同时计及蓄电池损耗特性，建立以综合发电成本最低、环境效益最好为优化目标的微电网优化模型。文献［3-5］以一个包含可再生能源、电储能、热电联产系统等的微电网为研究对象，分析了计及网内折旧、维护和热电联产系统燃料成本的各单元最佳出力。文献［6］构建了含电动汽车的动态环境经济调度模型，将“车-网”互动（V2G）功率以及常规机组出力作为决策变量，以总燃料费用和污染排放量作为优化目标，动态管理电动汽车的充放电行为。文献［7］从解耦热电耦合约束、提升电力系统调节能力的角度出发，提出了基于含储热热电联产机组与电锅炉的弃风消纳协调调度模型。文献［8］提出含储热、热电联产机组与电锅炉的弃风消纳协调调度模型。文献［9］利用通用分布模型拟合不同风电功率预测水平下的实际风电功率分布，并以此建立了考虑风电低估、高估成本的日前动态经济调度的随机优化模型。文献［10］建立了计及需求响应的风电与电动汽车协同调度的多目标优化模型，通过价格机制引导电动汽车入网，以负荷方差和车主支付费用最小为目标，并协调优化发电侧资源消纳风电。

以上文献在电热经济调度与风电消纳方面取得了一定进展，但是此类文献在调度过程中有4个问题尚未解决：通过合理调度，风电得到了消纳，但是风电的经济性没有量化，也没有将弃风与经济调度这2个目标结合起来；通过以降低储能损耗为目标进行调度，延长了储能的循环寿命，但是缺少电储能循环损耗、热储能散热损耗的经济性描述方法，也未能将储能运行成本统一到经济调度目标中；调度中若考虑电动汽车的作用，可能会使经济性更佳，已有的文献没有建立电动汽车调度成本模型；粒子群系列算法是求解优化问题的常用算法，但是对于多变量的高维优化问题，粒子群系列算法的收敛性有限。

为了解决上述问题，本文首先基于热电联产机组、风机、电储能和热储能、电动汽车等单元的出力模型建立其经济性模型；其次，综合考虑了燃煤成本、环境污染成本、储能损耗成本、弃风成本和电动汽车调度成本等，从全社会的角度出发构建了系统最优运行成本的一体化经济调度模型；然后，借鉴信息熵的概念，采用贪心变异策略，提出基于粒子维度熵的改进混沌粒子群优化CPSO（Chaos Particle Swarm Optimization）算法，求得系统内各单元最佳出力及总运行成本；最后，构造典型算例比较不同运行模式下的综合能源系统的运行成本，分析各设备单元在经济调度和消纳弃风方面的作用，并对比本文算法和其他几种算法的迭代结果，进一步说明本文所提方法的有效性与实用性。

1 系统各单元成本模型

区域电热综合能源系统主要包含热电联产系统、风机、电锅炉、电储能、热储能和电动汽车等单元，各单元通过热网和电网的能量传输流动联系起来，供给区域的电热负荷。

1.1 热电联产系统

1.1.1 煤耗成本

热电联产系统在时段t电热出力对应的燃料成本 CFU（t）可由式（1）表示：

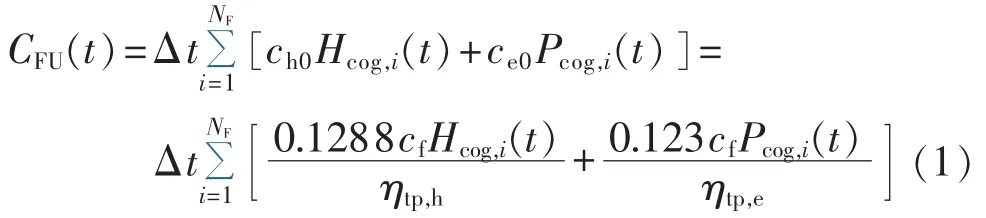
其中，NF为热电联产机组总台数；ch0和ce0分别为热电联产机组平均发热成本和平均发电成本；Δt为单位时段调度时长；cf为单位煤成本；Pcog，i（t）和 Hcog，i（t）分别为热电联产机组i输出的电功率和热功率；ηtp，h为机组供热效率；ηtp，e为机组发电效率。

电热比ηcog为热电联产机组电出力和热出力的比值，在“以热定电”模式下，热电联产机组i的电出力可由其热出力得到：

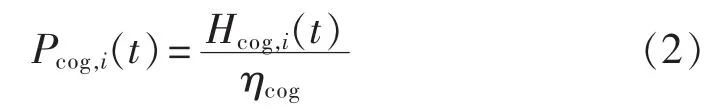
1.1.2 可控机组启停成本

根据文献［1］，机组启停成本计算公式如下：

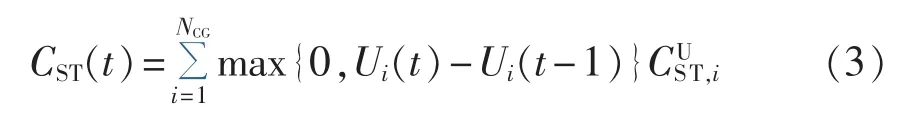
其中，NCG为可控机组总数；Ui（t）取值 0 或 1，为时段 t可控机组i的启停状态为可控机组i的一次启动成本。

1.1.3 环境污染成本

燃煤热电联产发电系统将排放NOx、SO2、CO和CO2气体，每个发电单元的污染成本为：

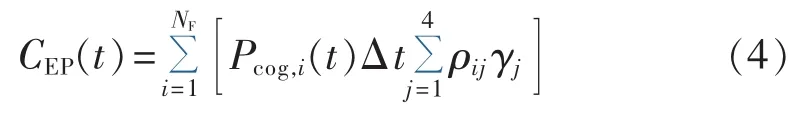
其中，ρij为热电联产机组i排放j类气体的排放因子；γj为j类气体的治污费用。

1.2 风机

由于无需购买一次能源，风机发电的运维成本实际上远低于火力发电的运行成本，但却出现风机上网电价较贵的现象，这主要是因为风机投资商是以盈利为目的的，风电售价中不仅包含运维成本，还包括建设成本，若从全社会角度出发，将上述两部分成本计入风机运行寿命周期内单位发电量上，即可得单位风电成本。弃风成本CWC是风电没有得到全部消纳所造成的经济损失，需通过风机实际发电量减去并网电量得到：

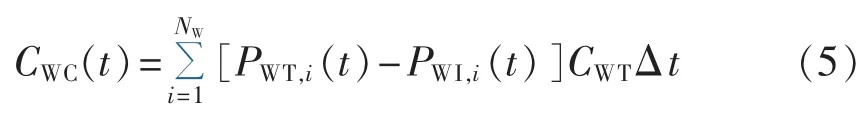
其中，NW为风机总台数；PWT，i（t）为时段 t第 i台风机的输出功率；PWI，i（t）为时段 t第 i台风机的并网功率；CWT为单位风电成本。

文献［11］考虑了风机建设成本、维修费用、人力成本、物价上涨指数、政府补贴等，计算出风电单位折算成本。但该模型的风机折旧年限过长，也没有考虑风机建设成本的残值。本文在文献［11］模型的基础上，结合风机的实际运行年限，考虑风机净残值，改进了风机年发电量的计算方法，建立了如下风机单位折算成本模型：

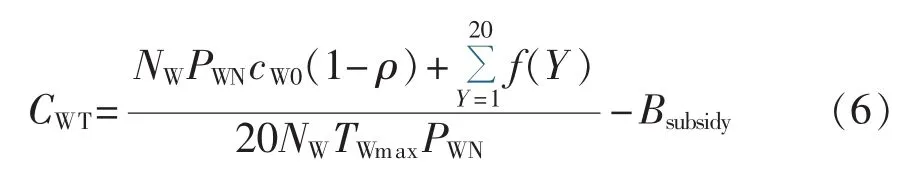
其中，PWN为单台风机满发出力，这里认为其等于风机装机容量；cW0为风机建设单位容量投资；ρ为风机净残值率；TWmax为风机年发电等效满负荷小时数；Bsubsidy为国家节能减排补贴；f（Y）如式（7）所示。

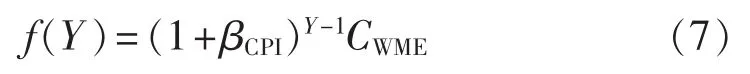
其中，Y为风机运行时间；βCPI为物价上涨系数；CWME为风机的年运行成本。

1.3 储能

为了描述储能的运行和损耗成本，本文利用储能建设费用建立其单次循环损耗成本模型，利用热电联产系统平均发电／发热成本建立储能能量传输损耗成本模型。

1.3.1 热储能

（1）热储能动态模型。

热储能主要包括大型蓄热罐、蓄热槽及蓄热式电锅炉等，其特性可描述成设备自身容量、输出输入能力和热效率等几部分之间的关系。其差分动态数学模型可表示为：

其中，HHS（t）为时段 t热储能容量；kLOSS为热储能散热损失率；Qst（t）、Qex（t）和 kst、kex分别为时段 t吸、放热功率及吸、放热效率。本文中kLOSS取为1%／h，kst、kex取 90%。

（2）热储能损耗成本。

本文以水作为储热介质，无需设置换热器，并且储热装置主要是针对城市小区域进行供热。储热装置的循环寿命损耗相对于储电装置较小，本文不予考虑。储热装置损耗主要为闲置散热成本与热传输损耗。综上，热储能损耗可由式（9）表示。

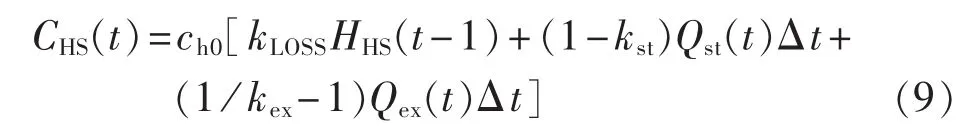
1.3.2 电储能

（1）电储能动态模型。

储电装置只考虑铅酸蓄电池LB（Lead-acid Battery），其动态模型［12］与储热装置类似，可由式（10）表示。

其中，EES（t）为时段 t储电量；Pst（t）、Pex（t）和 δst、δex分别为时段t的充、放电功率及充、放电效率。本文中δst、δex均取 90%。

（2）电储能损耗成本。

铅酸蓄电池的自放电率较小，因此不考虑自放电损耗，储电装置的充放电成本损耗主要为储电装置寿命损耗成本CES1与电传输损耗成本CES2。

文献［13］采用雨流计数法计算电池放电深度DoD（Depth of Discharge），拟合电池使用寿命与放电深度之间的关系。采用四阶函数表征循环寿命与放电深度D的关系：

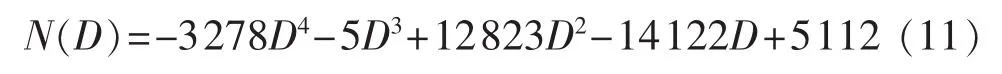
当蓄电池在短时间Δt内参与负荷调节时，只有充电或放电半个过程，因此在计算循环损耗时，需引入调节系数μ1。电量变化ΔSOC即为电池的放电深度D，对应的电池寿命损耗成本为：

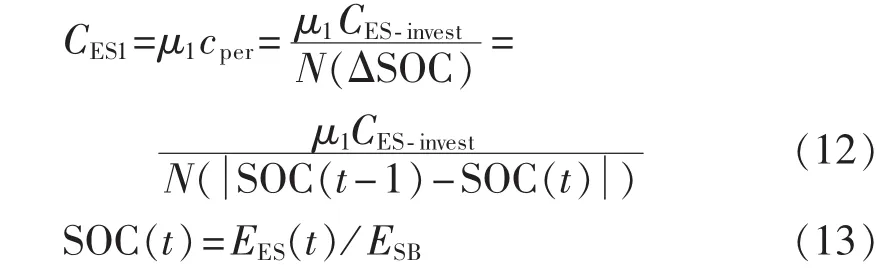
其中，cper为蓄电池每次循环费用；CES-invest为蓄电池的一次性购置费用；ESB为蓄电池容量。

结合式（10），可以得到电池循环损耗成本与充放电功率的关系为：

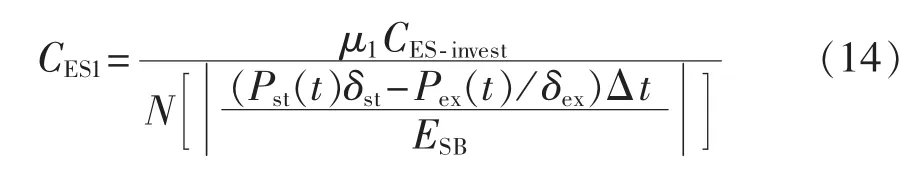
电传输损耗是由于蓄电池传输效率达不到100%导致的能量损耗，可由下式表示：

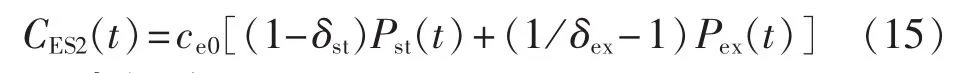
1.4 电锅炉

电锅炉是将电能直接转化为热能的装置，其在运行过程中只有维护成本，成本模型可表示为：

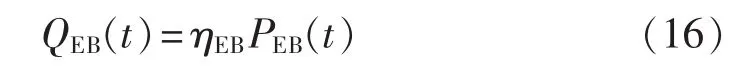
其中，QEB（t）为时段 t电锅炉的热出力；PEB（t）为时段t电锅炉的耗电功率；ηEB为电锅炉效率。

1.5 电动汽车

本文在用户侧引入V2H（Vehicle to Home）系统，鼓励固定时段非行驶状态的电动汽车参与系统调度。

1.5.1 电动汽车电池动态模型

电动汽车电池的动态模型可以描述其电池状态，可表示为：

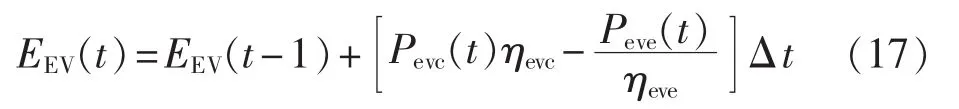
其中，EEV（t）为时段t电动汽车电池内储存的电量；Pevc（t）与 Peve（t）分别为电动汽车从家庭用户获得的充电功率和电动汽车向家庭用户输出的放电功率；ηevc与ηeve分别为电动汽车充电与放电的效率系数。

1.5.2 电动汽车调度成本

电动汽车在返回停车场后，应充电以满足下一日行驶需求。在这个过程中，电动汽车电池可以参与系统调度，响应各时段的充放电功率大小。从全社会的角度考虑，电动汽车参与调度的成本就是电动汽车电池的循环损耗成本。假设电动汽车采用恒功率慢充／放电，电池寿命损耗只与电池循环次数有关，电动汽车电池由SOCEVmin充电至SOCEVmax最多可循环NEV次，电池容量为EEV，则可以由式（18）表示电动汽车电池单位电量循环损耗成本。

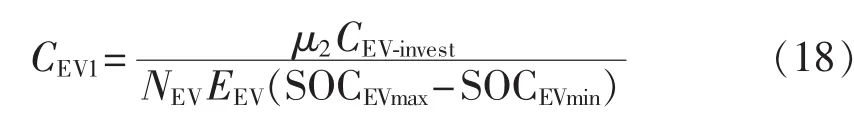
其中，CEV-invest为电池的一次性购置费用；μ2为综合修正系数。

2 区域综合能源系统经济调度模型

2.1 目标函数

结合各单元成本模型，综合能源系统经济调度的目标是在满足系统运行约束的条件下，通过合理安排各单元的出力，使全社会日运行成本最低。目标函数如下：

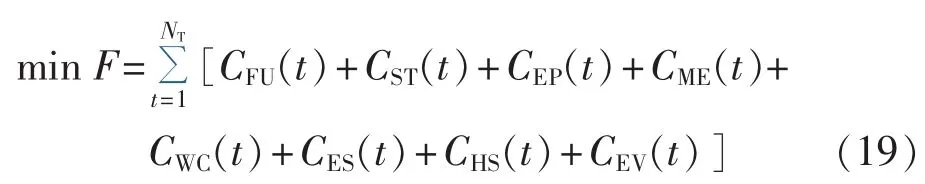
其中，F为全社会运行成本；NT为调度时段总数；CME（t）为时段 t各单元运维成本，如式（20）所示。

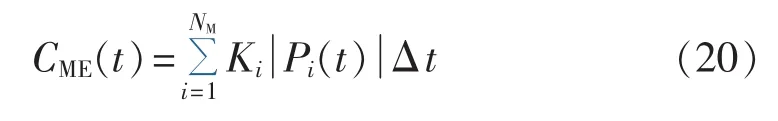
其中，NM为设备单元总数；Ki为第i类设备的维护成本系数；Pi（t）为第i类设备在时段t的输出功率。

2.2 约束条件

模型的约束条件需要考虑综合系统中各子系统相应的约束条件、电力系统和热力系统的网络约束条件。

2.2.1 电功率平衡约束

在地区综合能源系统中，参与调解负荷平衡的设备有热电联产机组、风电机组、储电装置、电动汽车和电锅炉。具体电功率平衡表达式为：

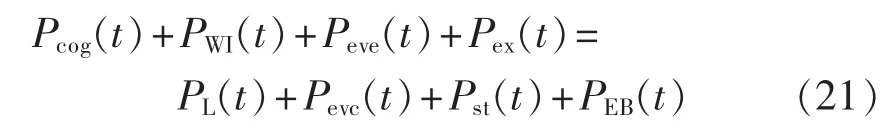
其中，PL（t）为时段 t系统的用电负荷；PWI（t）为时段 t系统消纳的风电。

2.2.2 热功率平衡约束

参与调解热负荷平衡的设备有热电联产机组、储热装置和电锅炉。具体热功率平衡表达式为：

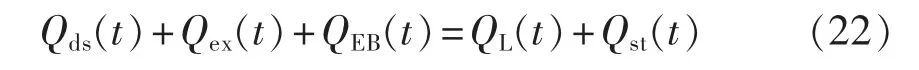
其中，Qds（t）为时段t热电联产机组输出的热功率中针对热负荷的直供热部分；QL（t）为时段t的热负荷。

2.2.3 其他约束

其他约束包括热电联产系统供电／热出力区间约束、可控机组出力爬坡约束、机组启停次数约束、储能容量约束、电动汽车电池的容量约束、储能装置功率传输约束、电动汽车电池功率传输约束、电锅炉出力约束、电力和热力网传输支路的潮流约束等。

3 求解算法

粒子群优化PSO（Particle Swarm Optimization）算法是一种基于群体智能的随机搜索算法。CPSO算法［14］在PSO算法的基础上引入混沌搜索，在变异过程中避免产生重复解，从而改善了PSO算法容易陷入局部收敛的缺点。但是CPSO算法的变异概率始终保持不变，当种群多样性较小时，依然以较低的概率变异，则易陷入局部最优。

3.1 粒子维度熵

为了衡量种群多样性，一些算法引入了信息熵的概念，一个系统的信息熵可由式（23）表示。

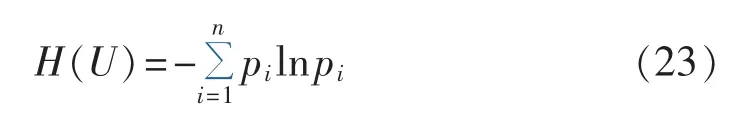
其中，U为所有可能输出的集合；pi为第i类输出的概率函数。一个系统越混乱，信息熵就越高且越接近于1，所以，信息熵也可以作为系统有序化程度的一个度量。

假设粒子群在一个n维空间中搜索，种群中包含m个粒子，文献［15-16］引入了种群熵以改进算法，这些算法是以m个粒子适应度的丰富度来衡量种群信息的多样性，这种处理方式有一定缺陷：当种群中各粒子在n维空间中的坐标差异较大（各粒子相对距离较远），但由于适应度函数的计算方法等缘故，这些粒子适应度差异却较小时，种群熵会偏高，在此时选择变异不仅会使种群偏离原有的正确寻优轨迹、延长计算时间，还有可能会在变异后缩短各粒子的相对距离，降低种群多样性。本文根据粒子各维度坐标差异性，引入如下粒子在维度d上维度熵的确定方法：

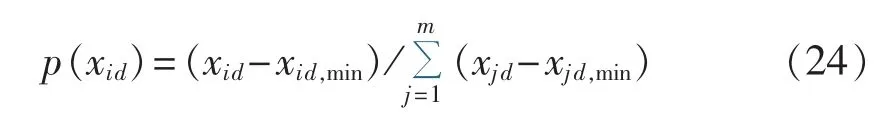
其中，xid为第i个粒子在维度d上的位置坐标；p（xid）为对应位置坐标的概率函数；xid，min为xid的最小值。种群包含n个粒子维度熵，归一化后的粒子维度熵可由下式表示：

设置维度熵上限为Emax，在迭代过程中若维度d的维度熵E（xd）>Emax，则对该维度的部分粒子坐标进行混沌变异。

3.2 基于粒子维度熵和贪心策略的CPSO算法

为了缩短迭代的收敛路径，可采用图1所示贪心变异策略［17］对部分适应度较差的个体坐标进行如式（26）所示的混沌变异。当种群较小时，应设置较高变异个体比例，提高种群多样性；当种群较大时，可适当降低变异个体比例。本文种群大小为50，变异个体比例选取为种群大小的80%。

其中，k 为迭代次数；xid，max为 xid的最大值；z（k+1）为第k+1次迭代的Logistic混沌方程取值，其表达式如式（27）所示。

它是典型的混沌系统，当 μ=4 且 0≤z（0）≤1（z（0）≠0.5）时，z的取值永远不会重复。

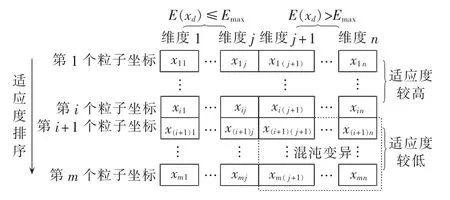
图1 贪心变异策略示意图Fig.1 Schematic diagram of greedy mutation strategy

本文采用基于粒子维度熵的改进CPSO算法对模型进行求解。综合能源系统的调度模型求解是一个单目标优化问题，优化变量包括各时段热电联产机组和电锅炉出力、储能装置的储放能功率、电动汽车的充放电功率等。计算步骤如下。

a.初始化粒子群，确定每个粒子的位置初值。

b.根据适应度评价函数即式（19），计算每个粒子的适应度值。

c.更新粒子个体极值pid和种群全局极值pgd，保留最优的个体极值和全局极值。

d.根据式（28）、（29）更新粒子的速度和位置。

其中为第i个粒子在第k+1次迭代中维度d上的速度；w 为惯性权重；η1、η2为加速系数；r1、r2为0～1之间的随机数。

e.根据式（24）和式（25）计算 n个粒子维度熵，若某一维度熵E（xd）＞Emax，则对该维度适应度较差的80%个体的坐标进行如式（27）所示的变异。

f.判断是否达到迭代停止条件，若满足终止条件，则停止计算；否则转步骤b。

4 算例分析

4.1 基本算例

以我国北方某城市地区为例，区域由热电联产机组通过“以热定电”方式供热、供电，并配置20×2 MW的分布式风电机组组成小型风电集群。模型参数如下：Δt＝15 min；cf＝1000 元 ／t；ηtp，e＝0.3539；ηtp，h＝0.8924；ηcog＝1；TWmax＝2000 h；cw0＝8300 元 ／kW；βCPI＝5%；风电场的年运行成本为其初始投资的5%；Y＝9 a；ρ＝3%；Bsubsidy＝0.1 元 ／（kW·h）［11］。 环境污染系数［2］见表 1。

表1 污染物治理成本及排污系数Table 1 Pollutant treatment cost and emission factor

该地区冬季某典型日热负荷与电负荷分布情况如图2所示，风机出力如图3所示。在各单元出力日运行调度过程中，假设系统满足2个条件：各设备效率保持恒定；系统相对独立，产生的无法消纳的电能或热能将被废弃。

图2 负荷与热电联产机组出力Fig.2 Load and output power of CHP

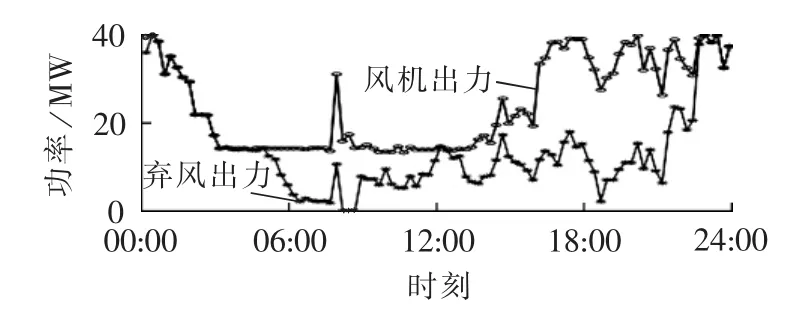
图3 风机出力与弃风出力Fig.3 WT output power and curtailed wind power

由图2可以看出，在“以热定电”模式下，热电联产机组出力几乎与热负荷曲线重合。由图2和图3可以看出，午间和晚间电负荷较高，在此期间部分风电被消纳，其余时刻大部分风电都被舍弃，一天弃风电量可达340.46 MW·h。

4.2 改进算例

为了分析各单元在优化调度和降低弃风方面的作用，设定2种运行模式下的算例进行对比。算例1：在基本算例运行模式的基础上加入储能和电锅炉，电储能和电锅炉参与电力平衡调度；热储能和电锅炉参与热力平衡调度。算例2：在算例1运行模式的基础上加入电动汽车，电动汽车电池在固定时段参与系统调度。各单元运维参数［1-8］见表2。

表2 各单元运维参数Table 2 Operational parameters of different units

4.2.1 算例1结果

算例1的运行结果如图4、5所示。算例1的弃风电量为49.05MW·h，与基本算例相比减少了约85%的弃风电量。在模型中加入储能和电锅炉，改变了原有的负荷曲线，形成了新的负荷分布。

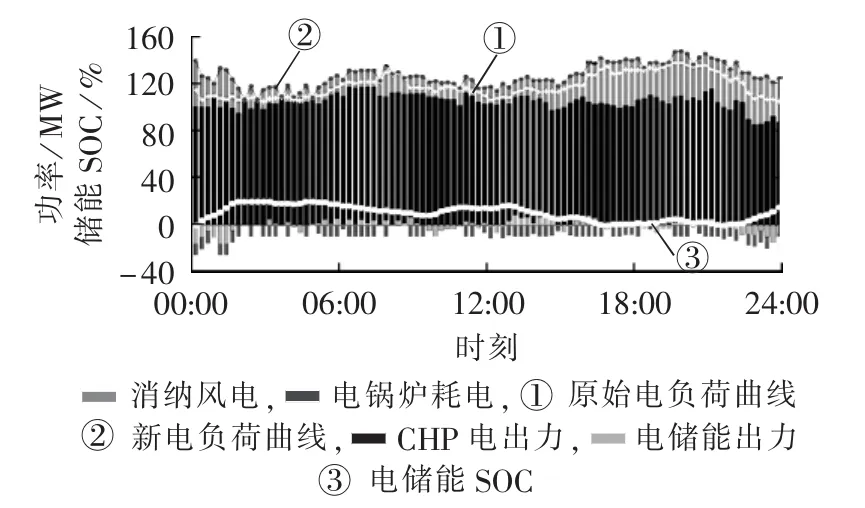
图4 算例1电负荷平衡情况及电储能SOC变化曲线Fig.4 Power load balance and SOC curve of ES in Case 1

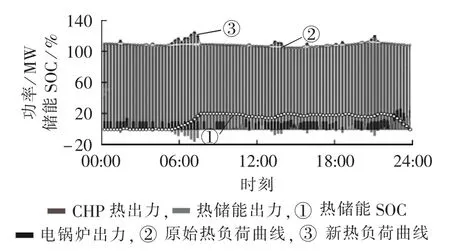
图5 算例1热负荷平衡情况及热储能SOC变化曲线Fig.5 Heat load balance and SOC curve of HS in Case 1

由图 3和图 4可知，00∶00— 02∶00和 22∶00—24∶00 2个时段，风机出力旺盛，电负荷较低而热负荷较高，此时电锅炉出力与电储能出力配合，提高了该时段的电负荷，为风电消纳提供了空间。由图5可知，22∶00— 24∶00，热储能出力增大以满足该时段的热负荷，降低了“以热定电”模式下的热电联产机组出力，不仅减少了燃煤成本，还消纳了一部分风电；06∶00— 08∶00，电负荷较高而热负荷较低，热储能与电锅炉配合提高了该时段热负荷，使电热负荷保持同步，提高热电联产系统的利用率。

4.2.2 算例2结果

算例2中电动汽车型号为比亚迪e6，CEV-invest为10万元，μ2取0.2，电池由SOC下限通过慢充方式充满大概可循环1000次，kEV取0.05。根据电负荷推算该城市约有100000人，人均电动汽车占有率为0.8%，则该区域有800辆电动汽车。假定电动汽车到达停车场的时间为 20∶00，剩余电量 30%，次日 05∶00 之前须充电至90%，在此期间电动汽车电池参与系统调度。算例2运行结果如图6、7所示。

图6 算例2电负荷平衡情况及电储能SOC变化曲线Fig.6 Power load balance and SOC curve of ES in Case 2

图7 算例2热负荷平衡情况及热储能SOC变化曲线Fig.7 Heat load balance and SOC curve of HS in Case 2

算例2的弃风电量为4.14 MW·h，风电几乎全部得到消纳。电动汽车电池可以看作固定时段充放电的电储能，算例2与算例1相比相当于扩大了电储能的容量，使电储能调节负荷的作用得到进一步强化，调度得到经济性更优的负荷曲线。由图3和图7可知，00∶00—05∶00，风机出力旺盛，电锅炉、电储能和电动汽车电池出力配合提高了电负荷，使该时段风电得到大幅消纳。由图 4 和图 6 可知，20∶00—24∶00，电动汽车电池的参与弱化了该时段电储能的作用，电储能出力较少，同时，电动汽车电池也对电锅炉出力和热储能出力的时空分布有一定影响。

4.2.3 算例结果对比

各算例的弃风量和运行成本分别如图8、表3所示。

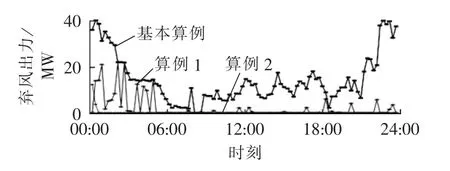
图8 各算例弃风出力Fig.8 Curtailed wind power for two cases

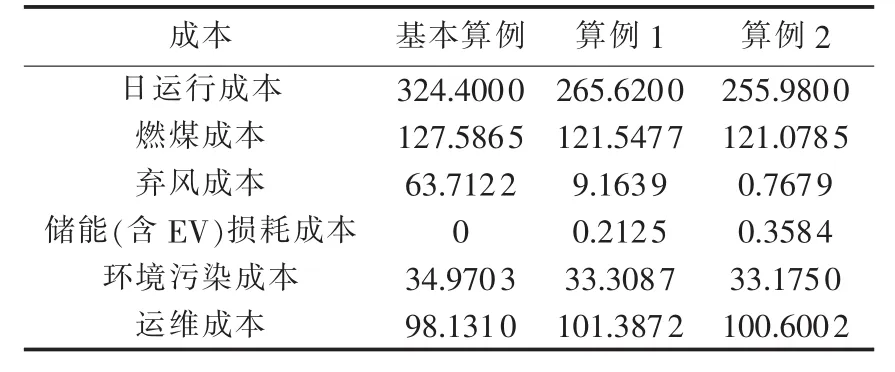
表3 各算例运行成本Table 3 Operational costs for two cases万元

机组启停成本设置较大，本文中通过各单元出力配合避免了热电联产机组的启停，因此机组启停成本为0。由图8可知，算例1与基本算例相比，各时刻弃风量都有所下降；算例2与算例1相比，主要是00∶00—05∶00的弃风得到消纳，其他时刻的弃风量也略有下降。由表3可知，由于算例1和算例2消纳了更多的风电，热电联产机组出力略有减少，与热电联产机组出力相关的燃煤成本和环境污染成本也相应减少。算例1和基本算例相比，日运行成本明显下降，而且储能损耗成本相对燃煤成本而言较小，证明储能在经济调度方面具有重要作用。算例2和算例1相比，尽管系统增加了约1461元的电动汽车调度成本，但弃风成本大幅减少，体现了电动汽车电池在调度中的作用。通过在算例中加入储能、电锅炉、电动汽车等装置，日运行成本和弃风成本逐步减少，验证了本文模型的有效性。

4.3 算法性能对比

选取CPSO算法、文献［16］基于种群熵的自适应PSO算法与本文采用的基于粒子维度熵的改进CPSO算法做对比。以算例2迭代情况为例，各算法运行过程见图 9，图 10 为时段 1（00∶00 —00∶15）电锅炉出力的粒子维度熵。

图9 3种算法迭代过程对比Fig.9 Comparison of iterative process among three algorithms

图10 3种算法粒子维度熵变化对比Fig.10 Comparison of particle dimension entropy variation among three algorithms

由图9可知，对于算例2这种96×4维的复杂优化问题，CPSO算法和文献［16］算法都很难求出其全局最优解。由图10可以看出，CPSO算法的粒子维度熵逐渐趋近于1，这表明随着迭代次数增加，种群多样性下降，算法陷入局部收敛；文献［16］算法在迭代过程中尽管会遵从一定规律降低粒子维度熵，但是由于其变异方式和条件无法满足优化问题的需要，也会陷入局部收敛；本文算法统计粒子维度而非适应度的信息熵，衡量的是粒子的多样性，并基于贪心策略对部分粒子进行混沌变异，使维度熵始终无法收敛于1。维度熵的波动体现了混沌变异的不重复性，波动始终处于0.96～1之间验证了变异策略的合理性。

5 结论

本文重点关注电热联合系统如何协调各单元出力以降低运行成本、提高能源利用率，利用合适算法求解高维优化问题，所得结论如下：

a.弃风不仅浪费风力资源，更有损经济成本，应对弃风情况给予足够重视；

b.储能、电锅炉、电动汽车等单元参与电热联合系统经济调度，可以有效降低系统运行成本，应鼓励电动汽车车主积极参与需求响应；

c.基于粒子维度熵的改进CPSO算法能够求解高维优化问题，在收敛性和收敛速度上都优于传统算法。

在电热调度过程中，本文将综合能源系统运营商、风机投资商和电动汽车车主视为一体，仅从全社会的角度考虑弃风经济成本和电动汽车调度成本。实际上，不同利益主体之间存在博弈关系，如何激励风机运营商、电动汽车车主参与调度，协调各主体的利益将作为下一步的研究方向。

参考文献：

［1］李正茂，张峰，梁军，等.含电热联合系统的微电网运行优化［J］.中国电机工程学报，2015，35（14）：3569-3576.LI Zhengmao，ZHANG Feng，LIANG Jun，et al.Optimization on microgrid with combined heat and power system［J］.Proceedings of the CSEE，2015，35（14）：3569-3576.

［2］胡晓通，刘天琪，何川，等.计及蓄电池损耗特性的微网多目标优化运行［J］. 中国电机工程学报，2016，36（10）：2674-2681.HU Xiaotong，LIU Tianqi，HE Chuan，et al.Multi-objective optimal operation of microgrid considering the battery loss characteristics［J］.Proceedings of the CSEE，2016，36（10）：2674-2681.

［3］陈洁，杨秀，朱兰，等.微网多目标经济调度优化［J］.中国电机工程学报，2013，33（19）：57-66.CHEN Jie，YANG Xiu，ZHU Lan，et al.Microgrid multi-objective economic dispatch optimization［J］.Proceedings of the CSEE，2013，33（19）：57-66.

［4］彭春华，谢鹏，詹骥文，等.基于改进细菌觅食算法的微网鲁棒经济调度［J］. 电网技术，2014，38（9）：2392-2398.PENG Chunhua，XIE Peng，ZHAN Jiwen，et al.Robust economic dispatch of microgrid using improved bacterial foraging algorithm［J］.Power System Technology，2014，38（9）：2392-2398.

［5］吴雄，王秀丽，王建学，等.微网经济调度问题的混合整数规划方法［J］. 中国电机工程学报，2013，33（28）：1-8.WU Xiong，WANG Xiuli，WANG Jianxue，et al.Economic generation scheduling of a microgrid using mixed integer linear programming［J］.Proceedings of the CSEE，2013，33（28）：1-8.

［6］朱永胜，王杰，瞿博阳，等.含电动汽车的电力系统动态环境经济调度［J］. 电力自动化设备，2016，36（10）：16-23.ZHU Yongsheng，WANG Jie，QU Boyang，et al.Dynamic environmental and economic dispatch of power system with EVs［J］.Electric Power Automation Equipment，2016，36（10）：16-23.

［7］崔杨，陈志，严干贵，等.基于含储热热电联产机组与电锅炉的弃风消纳协调调度模型［J］. 中国电机工程学报，2016，36（15）：4072-4081.CUI Yang，CHEN Zhi，YAN Gangui，et al.Coordinated wind power accommodating dispatch model based on electric boiler and CHP with thermal energy storage［J］.Proceedings of the CSEE，2016，36（15）：4072-4081.

［8］吕泉，姜浩，陈天佑，等.基于电锅炉的热电厂消纳风电方案及其国民经济评价［J］. 电力系统自动化，2014，38（1）：6-12.LÜ Quan，JIANG Hao，CHEN Tianyou，et al.Wind power accommodation by combined heat and power plant with electric boiler and its national economic evaluation［J］.Automation of Electric Power Systems，2014，38（1）：6-12.

［9］王豹，徐箭，孙元章，等.基于通用分布的含风电电力系统随机动态经济调度［J］. 电力系统自动化，2016，40（6）：17-24.WANG Bao，XU Jian，SUN Yuanzhang，et al.Stochastic dynamic economic dispatch of power systems considering wind power based on versatile probability distribution［J］.Automation of Electric Power Systems，2016，40（6）：17-24.

［10］侯建朝，胡群丰，谭忠富.计及需求响应的风电-电动汽车协同调度多目标优化模型［J］. 电力自动化设备，2016，36（7）：22-27.HOU Jianchao，HU Qunfeng，TAN Zhongfu.Multi-objective optimization model of collaborative WP-EV dispatch considering demand response［J］.Electric Power Automation Equipment，2016，36（7）：22-27.

［11］黄贵鸿，雷霞，杨毅，等.考虑风电与用户满意度的电动汽车两层智能充放电策略［J］. 电工技术学报，2015，30（5）：85-97.HUANG Guihong，LEI Xia，YANG Yi，et al.Two-layer smart charge-discharge strategies for electric vehicles considering wind generation and users’ satisfaction［J］.Transactions of China Electrotechnical Society，2015，30（5）：85-97.

［12］张晓波，张保会，吴雄.风光预测后微电网的优化运行［J］.电力自动化设备，2016，36（3）：21-25，40.ZHANG Xiaobo，ZHANG Baohui，WU Xiong.Optimal microgrid operation based on wind ／PV power prediction［J］.Electric Power Automation Equipment，2016，36（3）：21-25，40.

［13］韩晓娟，程成，籍天明，等.计及电池使用寿命的混合储能系统容量优化模型［J］. 中国电机工程学报，2013，33（34）：91-97.HAN Xiaojuan，CHENG Cheng，JI Tianming，et al.Capacity optimal modeling of hybrid energy storage systems considering battery life［J］.Proceedings of the CSEE，2013，33（34）：91-97.

［14］高鹰，谢胜利.混沌粒子群优化算法［J］.计算机科学，2004，31（8）：13-15.GAO Ying，XIE Shengli.Chaosparticle swarm optimization algorithm［J］.Computer Applications，2004，31（8）：13-15.

［15］姜毅，乐庆玲.基于信息熵的粒子群优化算法［J］.微型电脑应用，2008，8（5）：31-33.JIANG Yi，LE Qingling.Improved particle swarm optimization algorithm based on information entropy［J］.Microcomputer Applications，2008，8（5）：31-33.

［16］段晓东，高红霞，刘向东，等.一种基于种群熵的自适应粒子群算法［J］. 计算机工程，2007，33（18）：222-223.DUAN Xiaodong，GAO Hongxia，LIU Xiangdong，et al.Adaptive particle swarm optimization algorithm based on population entropy［J］.Computer Engineering，2007，33（18）：222-223.

［17］吴小珊，张步涵，袁小明，等.求解含风电场的电力系统机组组合问题的改进量子离散粒子群优化方法［J］.中国电机工程学报，2013，33（4）：45-52.WU Xiaoshan，ZHANG Buhan，YUAN Xiaoming，et al.Solutions to unit commitment problems in power systems with wind farms using advanced quantum-inspired binary PSO［J］.Proceedings of the CSEE，2013，33（4）：45-52.