基于能量网络理论的分布式供能系统分析

葛海麟 ，陈皓勇 ，文俊中 ，曾永浩 ，华 栋

（1.华南理工大学 电力学院，广东 广州 510641；2.广东电网有限责任公司禅城供电局，广东 佛山 528000）

0 引言

由于电力对人类社会的重要性，人们对电能的传递有着深入的研究，特别是对将电力工程理论与网络理论结合形成的电力系统分析理论［1］，为安全、可靠地利用电能奠定了理论基础。为了解决电能的供应问题，许多学者尝试将分布式能源作为电能源引入电力系统，相应的可靠性及运行优化等研究也逐渐深入［2-5］。分布式能源引入电力系统后，众多的分布式供能系统与电力系统共同构成了一个庞大的多能源综合利用系统，这对系统的运行优化及节能减排目标的实现提出了更高的要求。当前国内外学者对分布式供能系统的研究主要集中在分布式供能系统的能效分析及热经济性分析［6-7］、安全稳定性分析［8］及协调优化调度［9］等方面。 这些研究对分布式供能系统在工程领域的应用及推广起到了十分重要的作用，但在进行能效分析及热经济性分析时，仍局限于将分布式供能系统看作一个独立的个体。文献［10］将电网络与热网看作一个整体，提出了区域电力和供热系统的联立潮流求解方法。文献［11］从能量传递及转化本质的角度出发，将各种看似相互独立的能源系统整合成了一个相互联系及作用的整体，为多能源综合利用系统的建模、分析、运行与规划奠定了重要的基础。

能量的传递及转换过程，实质上也是炯用的传递及转换过程，研究炯用的传递及转换规律更具有理论和实际意义［12］。本文基于炯用传递理论，经过理论分析及推导得到炯用在线（管）路中的普遍化传递规律，建立炯用在线（管）路中的传递分析理论。为了证明能量网络理论的正确性及实用性，本文基于能量网络理论，对某个在工程实践上具有代表性的分布式供能系统进行建模、分析及计算，并采用将计算所得数据与系统实际运行数据对比的方式进行验证。最后，利用上述计算结果，对该分布式供能系统的各个环节进行炯用传递分析及计算，从做功能力损失的角度对系统的节能潜力进行判断，最终验证了“能质匹配”原则在分布式供能系统中的重要性。

1 能量网络基本理论

1.1 能量网络的基本概念

随着分布式能源的不断推广及应用，电力系统正发展成为一个庞大的多能源综合利用系统，与不同类型的能源系统共同满足用户的能源需求。这些不同类型的能源系统虽然有着不同的表现形式，但它们本质上传递的都是能量，本文将其统称为能量网络［11］，能量网络示意图如图1所示。

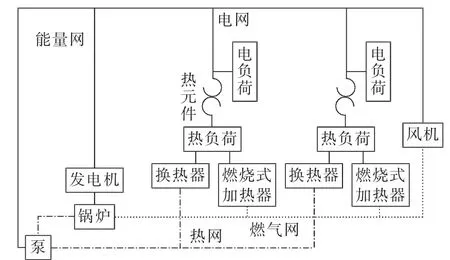
图1 能量网络示意图Fig.1 Schematic diagram of energy network

1.2 能量在线（管）路中的等效传递方程

能量网络是由传递线（管）路组成的，圆柱传递线（管）路如图2所示，图中X为强度量，Jx为广延量x的流密度矢量，下标A1和E1分别代表传递线（管）路的首端和末端截面。要研究能量在网络中的传递规律，必然要先研究能量在线（管）路中的传递规律。文献［11］基于文献［13］提出的广延量普遍化表达式Jx=KΔX（ΔX为强度量梯度），推导出能量在圆柱形传递线（管）路中的等效传递方程。

图2 圆柱传递线（管）路Fig.2 Cylindrical transfer line（pipe）

当广延量传递系数K为定值时（例如电能传递、稳态层流状态下的压能传递），能量在线（管）路中的等效传递方程为：

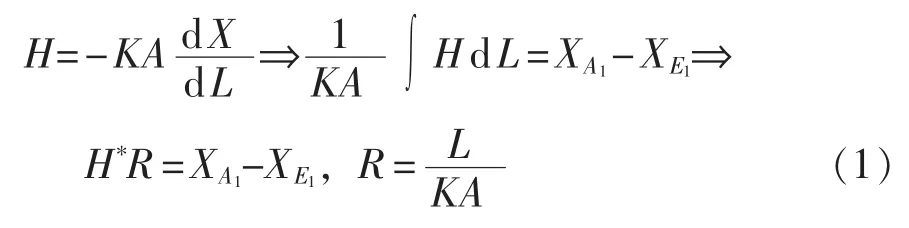
其中，L和A分别为传递线（管）路的长度和截面积；R为传阻，在电能传递过程中其为电阻，在压能传递过程中其为流阻；H*为积分 ∫HdL的拉格朗日中值，也即传递过程中的等效广延量流。

当广延量传递系数K非恒定，但能量传递系数λ=KX恒定时（例如热传导过程），能量在线（管）路中的等效传递方程为：

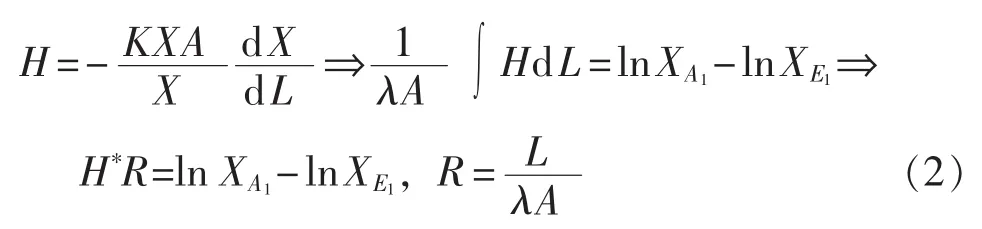
实际热量传递中，轴向上的温差很小，其引起的热量传递可忽略不计。传递过程中的热损失由热量径向传递引起，此时可对式（2）进行如下变换：

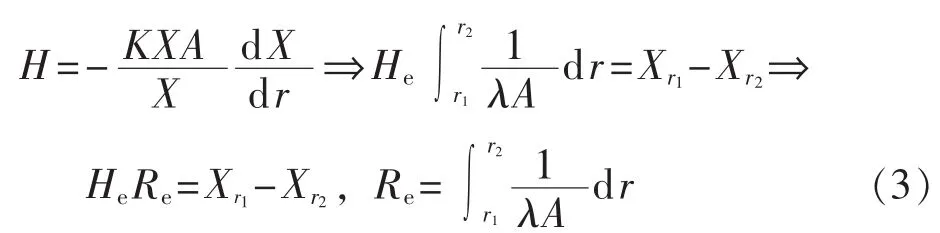
其中，下标r1和r2分别代表圆柱形传递线（管）路的内壁及外壁的半径；He、Re分别为热流量、热阻。

若进一步考虑管内流体与管壁之间和管外流体与外壁之间的热对流，可用多个串联热阻表示径向导热过程，径向热阻表达式为：

其中，λ为导热系数；h1、h2分别为内、外壁的对流传热系数。

能源有许多类型，但实际工程中能量的网络化传递主要依靠电网络和流体网络（如热网、燃气网等）。核能、风能、太阳能、水能等都必须先转化为电能或者热能再传递。电网络和稳态不可压缩流体网络的等效传递方程均为：

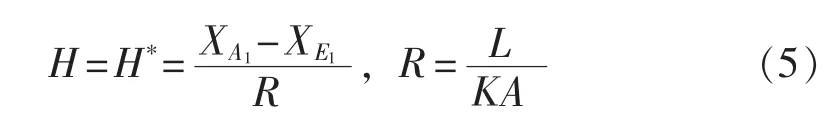
式（5）表示电网络方程时，X为电压，H为电流，K为电导率，该式即为欧姆定律［14］；表示流体网络方程时，X为压强，H为体积流量，K为体积传递系数率，该式即为不可压缩稳态层流的流动方程［15］。

1.3 广义的基尔霍夫定律

电网络是能量网络的一个特例，对应于电网络的基尔霍夫电压定律（KVL）和基尔霍夫电流定律（KCL），本文分别建立能量网络的基尔霍夫强度量定律（KIL）和基尔霍夫广延量定律（KEL）。基于广义的基尔霍夫定律能像列写电网络方程一样列写出能量网络方程，从而可以对能量网络中的各个参数进行求解。

a.基尔霍夫强度量定律：在能量网络的任何一个回路中，各段线（管）路强度量的变化量之和为0，即∑ΔX=0。

b.基尔霍夫广延量定律：对于能量网络中任何一个节点，流入该节点的广延量等于流出该节点的广延量。

1.4 能量网络方程的建立

由广义基尔霍夫定律可以列写出描述能量网络关系的方程组：

其中，A为关联矩阵；Bf为基本回路矩阵；H为广延量流量矩阵；ΔX为强度量差矩阵。根据能量在线（管）路中的等效传递方程，可以列写出描述传递线（管）路特性的方程组：

将这2个方程组组合就可以建立描述能量网络状态的能量网络方程。由此可见，能量网络方程与电网络方程具有相同的形式，因而对该方程组可解性的分析也与电网络方程组相似。对于一个有N+1个节点、B条支路的能量网络，根据广义基尔霍夫定律可以写出B个方程，B个方程中有2B个变量；再通过列写出B条支路的支路特性方程，联立则可对该能量网络方程实现求解。该方法与电网络中的2B求解法相似。

2 能量网络的炯用传递分析

2.1 炯用在线（管）路中的普遍化传递方程

对能量的评价包括能量的量及能量的质，与能量的量相比，能量的质（即炯用）或能量的品位更能深入地反映能量传递及转换过程中做功能力损失的实质。对于一个实际的能量网络，能量与炯用不是相互独立的，能量在线（管）路中的传递过程实质上也是炯用在线（管）路中的传递过程；某种能量和炯用的传递过程往往也会伴随有与其他类型能量和炯用的相互转化。与能量在传递及转换过程中始终守恒相比，炯用的传递及转换过程并不守恒，这表明了炯用传递过程必有其独特之处。因此，本文将根据炯用传递理论，将同一个传递过程中的能量和炯用统一起来，以得到更具有实用意义的能量和炯用的传递规律。

文献［13］提出了炯用的普遍化表达式：

其中，X0为强度量X的寂态值。

结合炯用的物理意义及定义可知，图2所示的圆柱形传递线（管）路中，能量由截面A1到截面E1的传递过程中产生的炯用损为：

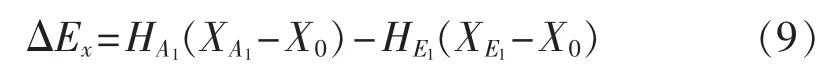
普遍化炯用传递及转换的动力学方程为［13］：

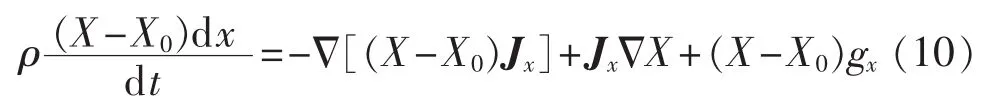
其中，ρ为介质的密度；gx为单位体积介质中广延量x的源强度。

式（10）等号左侧就是炯用随时间的变化率；等号右侧第1项表示通过体积元边界流入的炯用，第2项表示在强度量梯度的推动下与其他形式炯用之间的相互转换部分，第3项表示伴随着基本广延量的产生而由其他形式的炯用转化为该种形式的炯用。对该方程作体积分，整理简化后则可得到时变圆柱形传递线（管）路内的炯用平衡方程：

其中，xg为圆柱形传递线（管）路内广延量产生量关于长度L的函数。

对于时不变系统，式（11）等号左右两边均等于0，且dH=dxg，从而即可得到时不变系统圆柱形传递线（管）路内的炯用平衡方程：

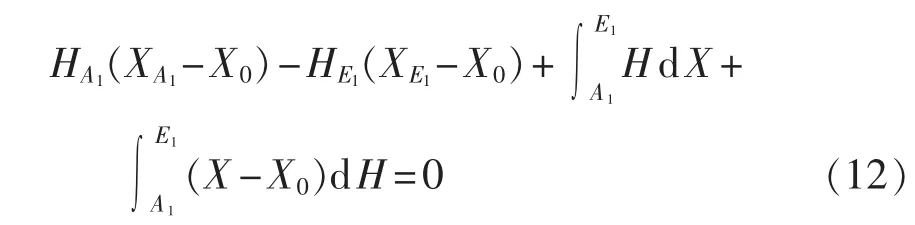
2.2 炯用在线（管）路中的传递过程分析

通过推导得到的式（11）及式（12），即炯用在线（管）路中的普遍化传递方程，是研究炯用在线（管）路中传递规律的重要依据。对于时不变系统，式（12）等号左侧前2项即圆柱形传递线（管）路中流动过程产生的炯用损 ΔEx，通过移项有：

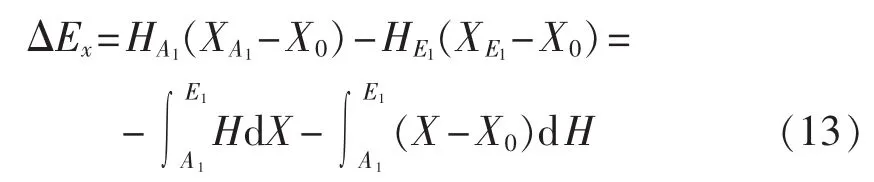
为了直观地理解能量和炯用在圆柱形传递线（管）路内传递及转换过程中的变化规律，以广延量H为横坐标、强度量X为纵坐标，作图得到能量在圆柱形传递线（管）路内由截面A1流向截面E1的参数变化曲线，如图3所示，图中虚线X0为该传递过程中强度量X的寂态值。

图3 参数变化曲线Fig.3 Variation of parameters

由能量公式可知，能量为状态参数X和H的函数，与过程无关，也即过程ae与过程abe是等效的（其中ab代表广延量不变的传递过程，be代表能量不变的传递过程）。过程be代表能量不变的传递过程，有SbmOc=SenOg。对比参数变化曲线易得，式（13）中代表传递过程中损失的炯用值；式（13）中代表传递过程中随着广延量的增加而由其他形式的炯用转化为该种形式的炯用。从而有：

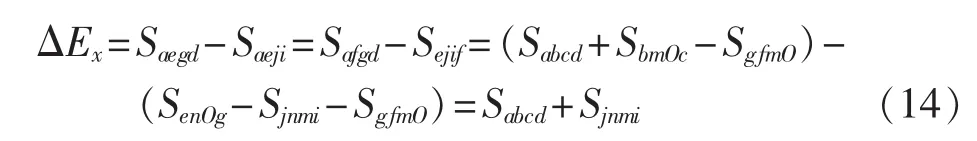
根据文献［11］的分析可知，式（14）中 Sabcd代表能量在线（管）路中传递所产生的损失ΔE；Sjnmi代表传递不可逆性所造成的损失的部分能量，由于Sjnmi可以表示为X0ΔH（ΔH为传递过程中线（管）路广延量的增加量），因此式（14）也可以改写为：

式（15）表明：与能量传递分析相比，炯用传递分析考虑到了传递不可逆性所造成的损失的那部分能量，更深刻地反映了能量传递过程中做功能力损失的实质。式（9）与式（15）是等价的，这表明以上的推导及分析是正确的，式（15）即是时不变系统的线（管）路中炯用损的普遍化表达式。

3 分布式供能系统的能量网络分析

3.1 能量网络的工程算例

为了验证能量网络方程的正确性及实用性，本节将对某供电局的分布式供能系统进行建模和计算，并通过计算所得数据与实际运行数据进行对比。在该分布式供能系统中，电能是通过线路传递的，冷量是以水为媒介通过管路传递的，分别形成了电网络和管网，而这2个网络也通过泵和用户（实验楼、综合楼、新楼）结合在一起，该系统实质上是一个能量网络。

本文研究的分布式供能系统的主要设备包括燃气轮机、溴化锂制冷机组、电制冷空调、泵等。系统使用燃气轮机燃烧天然气发电，将电供应给综合楼、实验楼和新楼，不足的电力由大电网络供应。此外，该系统利用天然气燃烧后的高温余气，通过溴化锂吸收式制冷机制冷，将冷量供应给新楼和综合楼，不足的冷量由电制冷空调提供。分布式供能系统的配置简图如图4所示。

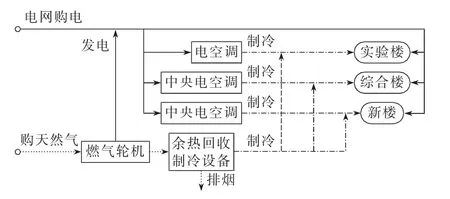
图4 系统配置简图Fig.4 Simplified diagram of system configuration

本文选取该系统在 2010年 9月 2日 12∶00∶00的数据进行计算，在该时刻溴化锂制冷机组只向新楼提供冷量（没有向综合楼和实验楼提供冷量），即能量网络中只有新楼，为了计算方便，本文在对该系统进行建模时，忽略综合楼和实验楼；虽然燃气轮机既供电也间接地供冷，但该系统是与大电网络相连接的，即可视为该分布式供能系统电能的供应是充足的，所以将燃气轮机和大电网络视为同一个电能源来处理；假设冷网中流体处于稳定层流状态。根据以上简化原则，该分布式供能系统的能量网络示意图如图5所示。

图5 分布式供能系统的能量网络示意图Fig.5 Schematic diagram of energy network of distributed energy system

图5中，S为电源；L为新楼中除去电制冷空调外其他电负荷；ARU为吸收式制冷机组；PCh为吸收式制冷机提供的冷量；PCe为电空调提供的冷量。整个系统运行状态是由PCh和PCe的比值决定的。图中实线代表电力线路，虚线代表冷水管路，电能与冷量通过水泵与冷负荷耦合在一起。由此可以画出该系统的网络图见图6。

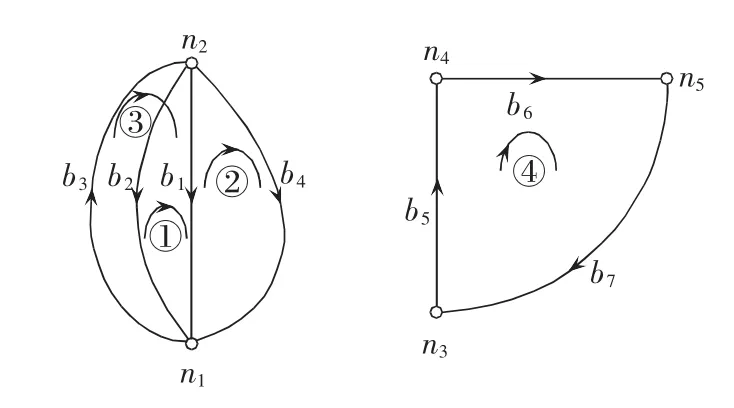
图6 系统网络图Fig.6 System networks

系统冷负荷由水冷空调和中央电空调系统共同满足，其中水冷空调系统制冷量PCh＝334.64 kW，中央电空调系统制冷量PCe＝540.54 kW。电源出口电压ΔX3＝-230.19 V，新楼其他电负荷的等效电阻为R2＝RL＝2.15 Ω，R4为等效可变电阻，其值受电制冷空调提供的制冷量影响，管路流阻 R6＝2.4×106Pa·s／m3、R7＝3.6×106Pa·s／m3，电制冷空调的能效比 γCOP＝4，水泵总效率η=0.52。

由于该能量网络中的强度量电压和压强属于不同的物理量，两者具有不同的物理含义，因此在数值上无法对它们直接进行比较，因而为了简化计算，引入电力系统分析中的标幺制计算方法［1］。

选取流量基准值 HPB＝10-3m3／s，压强基准值 ΔXPB＝103Pa，电压基准值 ΔXqB＝230 V，电流基准值 HqB＝1／230 A，流阻基准值 RPB＝106Pa·s／m3，电阻的基准值 RqB＝5.29×104Ω。

a.由 PCh＝ρCΔTH6，H5＝H6＝H7，求得：H5＝H6＝H7＝3.331×10-2m3／s。

对已知参数进行标幺化处理后得到：总冷负荷PCs＝8.7518×105p.u.；机组提供冷量 PCh＝3.3464×105p.u.；电空调提供冷量 PCe＝ 5.405 4 × 105p.u.；电压ΔX3s＝-1.001p.u.；冷水流量 H5s＝H6s＝H7s＝33.31 p.u.；电阻 R2s＝4.064×10-5p.u.；管路流阻 R6s＝2.4p.u.，R7s＝3.6p.u.。

b.列写能量网络方程组：

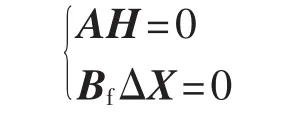
c.列写支路特性方程：ΔXi＝HiRi（i＝2，6，7）。

d.列写能量守恒方程：ΔX5H5+ηΔX1H1＝0。

e.列写电空调支路方程：PCe＝γCOPΔX4H4。

f.求解方程组。

强度量对比及广延量对比结果如表1所示。表中，ΔX1—ΔX4为相应支路的电压差；H1—H4为相应支路的电流；ΔX5—ΔX7为相应支路的压强差；H5—H7为相应支路的体积流量。

表1的对比结果表明：所有参数的误差绝对值均在5%以内，考虑到本文中建立的能量网络模型是基于稳态情况下的模型，模型本身并不完善，而实际运行过程是一个动态过程，所以计算数据与实际数据有误差是可以理解的。考虑到误差值不大，从而可以得出结论：能量网络方程是正确的。

表1 运行参数对比Table 1 Comparison of operating parameters

3.2 分布式供能系统的炯用传递分析

能量网络理论的建立为综合能源系统的建模、分析、运行与规划提供了重要的理论依据，但对工程实践上的分布式供能系统而言，单纯的能量分析及计算是不够的。要对节能潜力作出科学的判断及制定有效的优化措施，需要深入地探讨系统的炯用传递过程及其效率。分布式供能系统的炯用传递过程可分为2种：一为能量网络线（管）路中的炯用传递过程；二为能量转换设备的炯用传递过程。

3.2.1 能量网络线（管）路的炯用损分析

输电线路中的炯用损与电阻有关，电流在传递过程中产生热效应，线路中电炯用转化为热能耗散到环境中去。由于电压的寂态值X0＝0，将其代入式（15）可知，电能传递过程中线路产生的炯用损为：

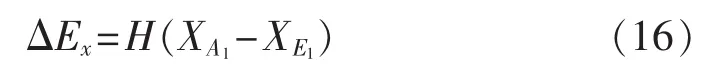
其中，H为流经线路的电流；X为电压。

压力的寂态值X0≠0，分布式供能系统管道内冷水是不可压缩的，此时ΔH＝0。同样地，将其代入式（15）也可得到式（16），此时H为流经管道的体积流量，X为压力。

冷水在管路传递过程中的能量损失为：

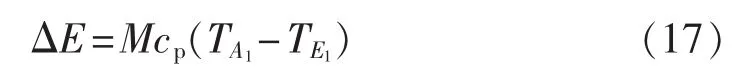
其中，M为管道内的质量流量；cp为定压比热容和分别为管段始端和末端处的流体温度，管段始端和末端处的流体温度满足［10］式（18）所示关系。

其中，T0为环境温度；λ为管道单位长度的传热系数。

在温度变化不大的情况下，比热容可视为定值，对于冷水管道其熵增为［16］：

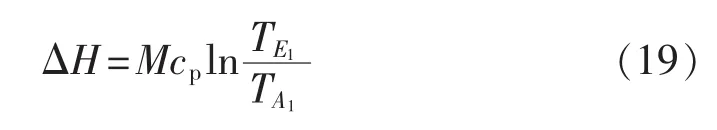
联合式（17）、（19），代入式（15），即可求得冷水在管道传递过程中产生的炯用损为：

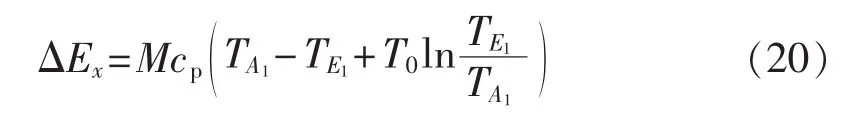
在分布式供能系统中电力线路较短，输电线路两端的电压降ΔX≈0，因此输电线路内的电炯用损失ΔExe≈0。分布式供能系统中通过冷水网络传递冷量，根据3.1节求得的系统运行参数，联立式（16）、式（18）和式（20），即可计算得到冷水管道的压炯用损失和冷量炯用损失。

计算该系统2011年9月2日12∶00∶00的数据。在该时刻，环境温度T0＝307.75 K，冷水机组出口温度T1＝280.25K，冷水机组入口温度为T2＝282.65K。根据式（18）和系统运行参数，即可推导出系统各冷水管道始端和末端的温度，代入式（16）和式（20）即可算得冷水管道支路b6和b7的压炯用和冷量炯用损失。其中管道支路b6的压炯用和冷量炯用损失分别为ΔExp＝2.658 kW 和 ΔExh＝4.989 kW，b7的压炯用和冷量炯用损失分别为 ΔExp＝3.986 kW 和 ΔExh＝4.239 kW。

通过上述分析可知，在分布式供能系统中输电线路电炯用损失可忽略不计，流体网络冷水管道的压炯用和冷量炯用损失较大，在规划运行过程中应采取措施减少炯用损，例如：规划阶段合理选择管道直径长度，运行阶段合理选择冷水供应温度等。

3.2.2 能量转换设备的炯用效率分析

为了找出系统存在的薄弱环节，提高能量利用效率，下文对系统中主要的能量转换设备进行炯用分析及计算。

a.系统电路消耗的炯用也即分布式供能系统输入的总电炯用为：

b.在分布式供能系统中，冷量炯用通过流体网络传递，并没有形成独立热网络，而输入的冷量炯用是通过冷水机组带入网络的。冷水机组带入网络的冷量炯用可以由式（22）进行计算。

其中，qm为冷水的质量流量。

c.用户获得的冷量炯用包括2个部分：一部分是由电空调提供，另一部分是由水冷空调提供。这两部分冷量炯用如式（23）所示。

其中，Tco为室内空气制冷出口目标温度为空气的定压比热容为水冷空调出口冷气的质量流量。从而系统输出到用户的冷量炯用为：

联立式（21）—（24），代入具体某个时刻的数据，即可求得该分布式供能系统的炯用效率，结果如表2所示。

表2 系统炯用计算结果Table 2 Results of system exergy calculation

表2的计算结果表明，该分布式供能系统中水冷空调的炯用效率最高，中央电空调的炯用效率最低。要实现分布式供能系统总炯用效率的提高，在水冷空调系统能满足用户制冷需要的情况下，应尽量减少使用中央空调系统，降低对高品位电能的消耗，即在分布式供能系统中，在满足用户能量需求的前提下，根据不同的用能场合匹配相应品质的能量，即实现“能质匹配”，才能实现能量更有效的利用。

4 结论

本文基于炯用传递理论，经过理论分析及推导，得到炯用在线（管）路中的普遍化传递规律，建立炯用在线（管）路中的传递分析理论。为了证明能量网络理论的正确性及实用性，对某个在工程实践上具有代表性的分布式供能系统进行建模、分析及计算。分析结果表明：系统各个参数的误差绝对值均在5%以内。考虑到误差值不大，从而可以得出结论：能量网络方程是正确的。最后，对分布式供能系统的各个环节进行炯用传递分析及计算，从做功能力损失的角度对系统的节能潜力作出判断，最后验证“能质匹配”原则在分布式供能系统中的重要性。

参考文献：

［1］夏道止，李建华.电力系统分析［M］.北京：中国电力出版社，2004：46-53.

［2］魏昊焜，刘健，高慧.分布式电源的本地电压控制策略［J］.电力自动化设备，2016，36（9）：40-45.WEI Haokun，LIU Jian，GAO Hui.Local voltage control of distributed generations［J］.Electric Power Automation Equipment，2016，36（9）：40-45.

［3］邓建玲.能源互联网的概念及发展模式［J］.电力自动化设备，2016，36（3）：1-5.DENG Jianling.Concept of energy internet and its development modes［J］.Electric Power Automation Equipment，2016，36（3）：1-5.

［4］冉鹏，张树芳，郭江龙.分布式能源系统的研究现状与应用前景［J］. 热力发电，2005，34（3）：1-3.RAN Peng，ZHANG Shufang，GUO Jianglong.Distributed energy systems research status and application prospects［J］.Thermal Power Generation，2005，34（3）：1-3.

［5］蒋润花.分布式能源系统研究［D］.北京：中国科学院研究生院（工程热物理研究所），2009.JIANG Runhua.The research of distributed energy resources system［D］.Beijing：Graduate University of Chinese Academy of Sciences（Institute of Engineering Thermophysics），2009.

［6］张洪伟.分布式能源冷热电联产系统的热经济性研究［D］.武汉：华中科技大学，2005.ZHANG Hongwei.Heating-economicalanalysisofdistributed energy system［D］.Wuhan：Huazhong University of Science&Technology，2005.

［7］吴波.分布式能源冷热电多联产系统能效分析与可比性方法研究［D］. 北京：北京科技大学，2015.WU Bo.Energy effect analysis and comparable methodology study on CCHP based on distributed energy system［D］.Beijing：University of Science and Technology Beijing，2015.

［8］付超，陈柔伊，柳勇军.含多种分布式电源的微网系统孤岛运行安全稳定性［J］. 南方电网技术，2013，7（4）：71-74.FU Chao，CHEN Rouyi，LIU Yongjun.The stability of islandedoperation microgrid with various types of distributed energy sources［J］.Southern Power System Technology，2013，7（4）：71-74.

［9］龚锦霞.含分布式能源的电网络协调优化调度［D］.上海：上海交通大学，2014.GONG Jinxia.Coordinated optimal dispatch of the power system including distributed energy resources［D］.Shanghai：Shanghai Jiao Tong University，2014.

［10］LIU X，JENKINS N，WU J，et al.Combined analysis of electricity and heat networks［J］.Energy Procedia，2014，61：155-159.

［11］陈皓勇，文俊中，王增煜.能量网络的传递规律与网络方程［J］.西安交通大学学报，2014，48（10）：66-76.CHEN Haoyong，WEN Junzhong，WANG Zengyu.Transfer laws and equations of energy network［J］.Journal of Xi’an Jiaotong University，2014，48（10）：66-76.

［12］项新耀.炯用传递方程及炯用传递分析［J］.大庆石油学院学报，1998，22（2）：3-7.XIANG Xinyao.Exergy transport equation and exergy transprort analysis［J］.Journal of Daqing Petroleum Institute，1998，22（2）：3-7.

［13］韩光泽.寂态热动力学基础理论研究［D］.广州：华南理工大学，2002.HAN Guangze.Study on the foundation of dead state thermodynamics［D］.Guangzhou：South China University of Technology，2002.

［14］邱关源.电路［M］.北京：高等教育出版社，2004：50-73.

［15］罗志昌.流体网络理论［M］.北京：机械工业出版社，1988：10-55.

［16］王修彦.工程热力学［M］.北京：机械工业出版社，2007：70-87.