基于能源集线器的区域综合能源系统分层优化调度

郝 然 ，艾 芊 ，朱宇超 ，伍 恒 ，梁中熙

（1.上海交通大学 电子信息与电气工程学院，上海 200240；2.西安交通大学 电气工程学院，陕西 西安 710049；3.南方电网广州供电局有限公司，广东 广州 510000）

0 引言

随着全球能源的深入渗透，能源利用向着多能协调、多能互补的方向发展，能源互联网成为多种能源网的集成发展方向［1］。传统的电力、热力和天然气网络相互独立的运行模式无法适应当前的能源生产和利用方式，2015年国家发改委能源局在促进智能电网发展的指导意见中明确提出“加强能源互联，促进多种能源优化互补”［2］。近年来，全球电能互联、区域多能源系统以及分布式多能源系统互联逐渐成为能源互联网3种主流的实现方式，综合能源系统ICES（Integrated Community Energy System）即上述后2种方式是能源互联网的重要载体，其核心是多能互补和能源阶梯利用［3］。

能源集线器EH（Energy Hub）最早由苏黎世联邦理工学院的Geidl M和Andersson提出［4］，它作为可以满足多种能源需求的能源转换单元［5］，可同时为不同能源的输入输出提供接口。EH对不同能量载体之间的功率转换建立了相应的耦合模型，从系统的角度看，耦合不同的能量载体相对于常规的去耦能量供应网显示出许多潜在的优点，冗余能流路径提供的一定程度的自由度为多能协同优化提供了空间。

目前，EH的分布式ICES的静态优化没有考虑燃气轮机与热电联产CHP（Combined Heat and Power）的协同优化，同时缺乏对CHP运行时机组热电比实时调整的考虑。在区域能源系统简化解耦的基础上，EH的输出量一般为CHP、燃气轮机和电网的总有功功率输出。一般的优化方法也通常停留在对基本EH模型［2］的优化上，对于区域内存在多个相同的能源转换单元，即多个相同能量转换器如何分配功率出力的问题没有进行深入考虑。此类场景考虑的需求侧响应也有局限性，常常忽略不同能源间用能替代这类广义的需求侧响应。

文献［6］运用EH对能源进行解耦优化，考虑了热电比的调整，但没有分析具体的网架和机组分配；文献［7］中的EH将区域内的CHP、燃气轮机和变压器等元件统一建模为单一能量转化元件，没有具体考虑区域内配置多个相同能量转化元件；文献［8］将多能流MEF（Multi-Energy Flow）的静态耦合模型应用于ICES的静态安全分析，但对于优化调度方面的应用没有过多涉及；文献［9-11］提出了包含扩展牛顿拉夫逊法的混合潮流计算方法，但至今少有文献将混合潮流运用到ICES的优化调度中；文献［12］分析了过量风电转换为热能的经济效益，但仅限于风机多能转化的内部收益，没有分析电网侧的调度收益；文献［13-14］同样分析了基于EH的优化问题，但其重点在于热能需求侧响应即周期性启停热负荷的优化，没有考虑热电比可调的情况，也没有结合具体网络算例分析。

针对上述情况，本文建立EH机组内部能效特性与外部能量分配的EH扩展模型和能量连接器动态模型，以经济成本最低、用能效率最高和区域内运行效率最高为目标，前2层是一个非线性双层规划（NBLP）问题，确定CHP用气比和热电比，第3层是考虑能源连接器动态过程的多目标优化问题，确定区域内多个能量转换器的功率配比。在区域EH的基础上完成热电解耦，将多节点耦合的复杂优化问题划归为统一解耦优化后再进行规划的问题。从仿真结果来看，优化方案满足了区域ICES的经济和环保要求，实现了电热气网络的优化运行。

1 EH扩展框架

EH包含2个基本要素：直接连接和经转换器连接。EH通过转换矩阵T将输入矩阵P混合输出能源L连接：L=TP。T为所有输入能源与输出能源间的转换效率，T中0代表对应2种能源间不存在转换关系。基于EH调度ICES运行要解决的根本问题就是在一定约束条件下寻找最优的转换矩阵T。

热电解耦矩阵如下：

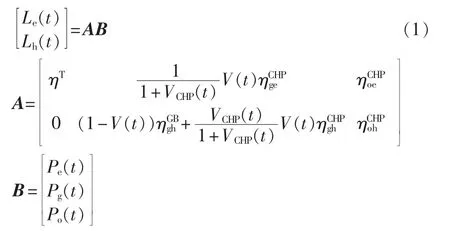
其中，Le、Lh分别为计及转移负荷的电、热实际负荷量；Pe、Pg、Po分别为区域能源网取用电厂电能、天然气和燃油一次能源的总能量；V为输入CHP的天然气功率占总购气功率的比例，满足0≤V≤1；热电比为CHP输出热功率与电功率的比值；为燃气锅炉（GB）供热效率；ηT为变压器效率和分别为天然气经过CHP转换成电和热的效率。图1为ICES能量枢纽框架结构，图中，VPg为输入CHP中的天然气功率，（1-V）Pg为输入GB的天然气功率；GDR（t）、TDR（t）分别为用能替代和电能转移2种需求响应。

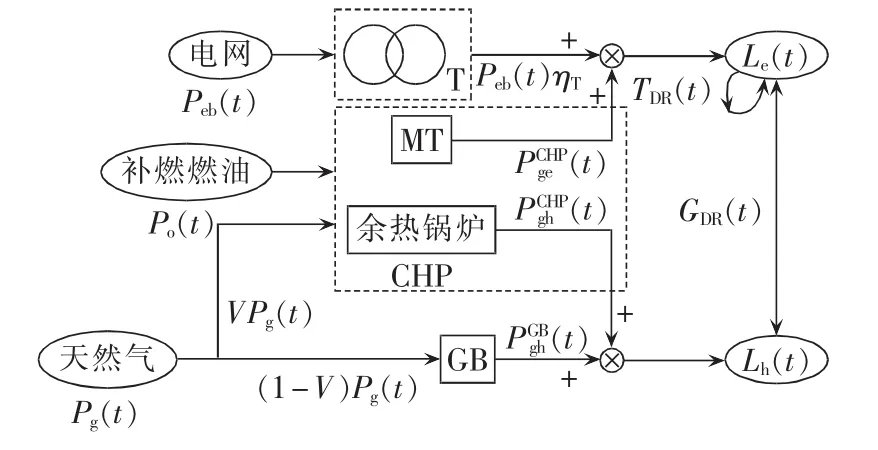
图1 ICES能量枢纽框架结构Fig.1 Structure of ICES energy hub frame

由于一般的冷热电三联产系统（CCHP）广泛采用吸收式制冷机，冷负荷可等效为热电负荷的叠加，因此这里仅讨论热电的解耦与优化调度。

CHP与一般发电机组的区别在于其可以通过余热锅炉收集发电多余热量，从而提高燃料利用率。余热锅炉可按有没有附加补燃设备分为无补燃余热锅炉和带补燃余热锅炉，无补燃余热锅炉的热电比一般认为无法更改，而带补燃装置的机组则可以通过补燃燃油在一定范围内改变热电比。一般情况下，燃油仅起到热电比调节的作用，并不能产生任何热电功率，因此燃油的热电转换效率均为 0。

2 基于EH的ICES分层优化模型

如图2所示，本文将整体优化模型分为多能分流层、能效优化层以及机组分配层，具体说明如下。

a.多能分流层以ICES综合用能成本最小为计算目标，将下层优化得到的CHP热电比代入优化计算。CHP机组是电热耦合元件，在热电价格不同时，系统综合用能成本对CHP和GB的实时天然气用能比的敏感程度最高，设置CHP和GB的实时天然气用能比为本层优化输出量，并将优化结果作为已知量代入下层优化模型。

b.能效优化层在上层优化给出CHP和GB的天然气用能比的基础上，最大化ICES用能效率。变压器、余热收集以及GB的能量转化效率较高（在90%左右），CHP机组发电能量转化效率较低（在36%左右），系统用能效率对CHP机组的实时热电比敏感度较高，设定CHP热电比作为本层优化输出量，并将优化结果作为已知量代入上层优化模型。

c.机组分配层根据前2层的优化计算结果，建立动态能量连接器模型，以同类机组功率分配为优化量，选取多能网运行评价指标（如线路损耗、热损和天然气网节点压强偏移等），实时优化综合能源网的运行状态。

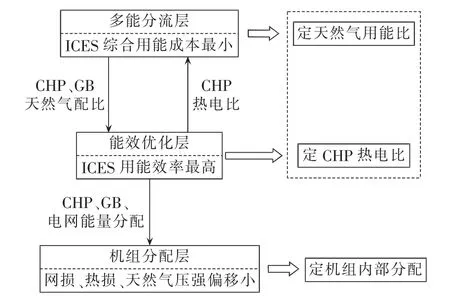
图2 IECS分层优化模型Fig.2 Hierarchical optimization model of IECS

2.1 多能分流层优化

（1）目标函数。

上层优化以用能成本最小为目标，用能成本包括综合运行成本C（t）和污染物排放成本P（t）。本层优化的决策变量为输入CHP的天然气功率占总购气功率的比值 V（t）。

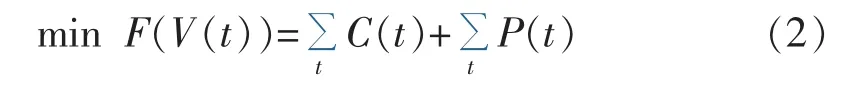
其中，C为综合运行成本；P为污染物排放成本。

综合运行成本考虑购能成本C1、设备折旧成本C2以及需求侧响应收益CDR，即C=C1+C2+CDR。

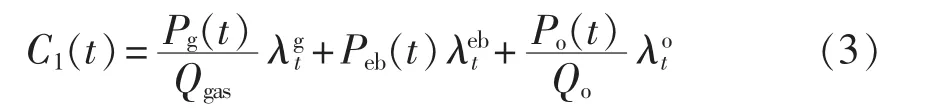
其中，C1（t）为购能成本，等式右侧3项分别为购气成本、电价成本和补燃燃油成本分别为天然气价格、电网实时电价和补燃燃油价格；Qgas为天然气的低热值，取 9.97 kW·h／m3；Qo为燃油低热值，取11.917 kW·h／kg；Po（t）为响应油耗。

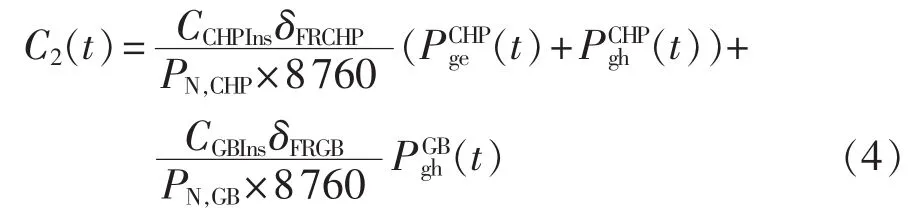
其中，C2（t）为 CHP 和 GB 的设备折旧成本；CCHPIns和CGBIns分别为CHP和GB单位容量安装成本；PN，CHP和PN，GB分别为 CHP和 GB的最大输出功率；δFRCHP和δFRGB分别为CHP和GB的资本回收系数，可由式（5）得到。

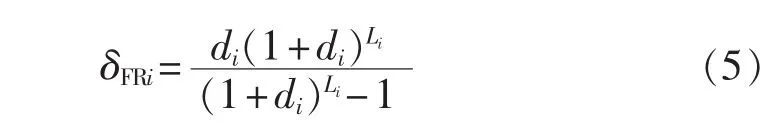
其中，di（i=CHP，GB）为相应发电类型 i的年折旧率，本文中CHP和GB的年折旧率均取为0.1；Li为发电类型i的折旧年限。

其中，CDR（t）为需求侧响应收益，包括CHP发电收益、用能替代收益和电能错峰收益；λIDR为CHP发电上网电价高于普通电价的部分。

其中，Pp（t）为污染物处理成本分别为GB、补燃装置、CHP以及电网电能污染物环境成本和生产单位能量的污染物排放强度（单位为 kg／（kW·h）），i表示污染物种类，包括CO、SO2和 NOx。 根据文献［13］可得，GB、补燃装置、CHP以及电网单位功率的发电污染物治理成本分别为 CGB、Co、CCHP和 Ceb。

（2）约束条件。

a.综合需求侧响应约束。

针对区域ICES，用户参与需求侧响应不再仅限于传统的需求侧响应。对于传统电能弹性负荷，用户响应行为具体表现在：在用电高峰时削减部分不必要负荷；将部分负荷从用电高峰转移至用电低谷时段。传统电能弹性负荷表现为用户对电负荷在时间尺度上的响应，这是区域综合能源用户需求侧响应的一种方式；另一种方式是用户在电价较高时将一些电负荷改用热或者在电价较低时将部分热负荷改用电，这时的弹性负荷不仅是电负荷，本文将这类需求侧响应称为广义需求侧响应，详见图3。

图3 综合需求侧响应示意图Fig.3 Schematic diagram of integrated demand-side responses

根据综合需求侧响应的特性建立ICES需求侧响应模型。设PGDR（t）为t时刻电能替代热能的功率，PTDR（t）为t时刻用户用电减少的功率。具体响应模型为：

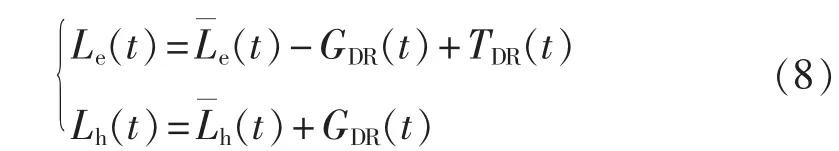
其中分别为电、热负荷的预测值。

b.系统约束。

为了降低区域能源系统对于地区电网的影响，电力市场规定区域购电量在一定范围内，设定区域购电量浮动极限。

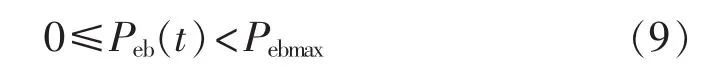
根据机组特性，CHP和燃气轮机电能出力上、下限约束分别为：

c.CHP热电比调节特性约束。

根据文献［14］提供的补燃机组实验数据，用线性模型对CHP补燃率A（%）、热电比VCHP、响应油耗量 Po（t）进行拟合得：

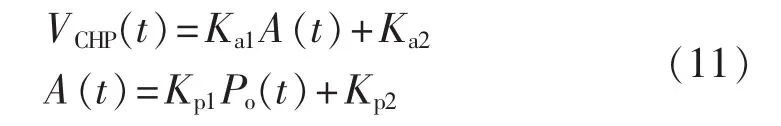
其中，Ka1、Ka2、Kp1、Kp2为补燃机组特性拟合后的模型参数。

将式（11）代入式（1）并由热电比定义可得：

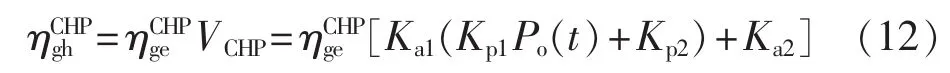
最大补燃率约束：

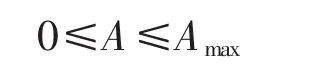
其中，Amax为内置补燃装置的最大补燃率，单位为%。

2.2 能效优化层

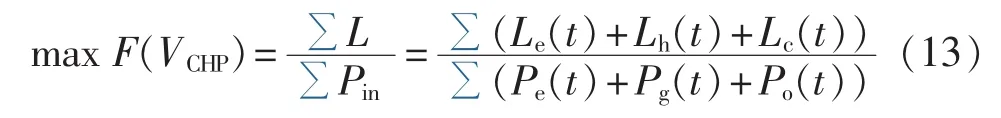
CHP的热效率和发电效率差别较大，由文献［15］可知，综合能源网能效对CHP热电比的敏感度最大，本文中能效优化层的优化目标为能源利用率最高，决策变量为CHP热电比。定义目标函数：其中，F为总的能量输出与能量输入之比。多能分流层和能效优化层的决策变量互为对方的已知量，多能分流层和能效优化层的求解是一个典型的NBLP问题。NBLP是一个 NP（Non-deterministic Polynomial）问题，由于下层模型具有连续、非线性和凸函数的特征，并且下层模型在可行域可导，根据KKT最优化条件可知下层模型极点处导数为0，可利用KKT模型对下层目标函数和约束建立拉格朗日函数，算法详见文献［17］，设下层有N个约束，具体优化模型为：

设为多能分流层优化的可行解，λT为拉格朗日乘数向量。对于固定的由最优性条件可知，能效优化层的问题等价于求解如下K-T点问题，将K-T条件等价为：

其中，λT=（λ1，λ2，…，λN）为拉格朗日乘数向量。

对下层决策变量VCHP求偏导的具体表达式为式

将拉格朗日函数作为上层多能分流的可行性度量，可行域为满足L=0的所有未知量集合。

2.3 机组优化分配层

在新的IECS的框架下，各类能源转换设备紧密耦合给最优潮流和运行方式的决策带来了一些难题。电力网络直接将电能传输至负荷侧，其中一部分发电节点CHP与热力系统耦合，热力系统又包括热源、热负荷、供热回路和回热回路，热源均视为天然气网络的负荷节点，天然气网络又由气源、管道、压缩机和天然气负荷组成。传统的潮流分析方法仅适用于纯电力系统，在IECS中的应用有很大的局限性。电热耦合系统的稳态混合潮流MCPF（Multi-Carrier Power Flow）模型［18］为IECS调度决策提供了新的思路。

考虑动态能源连接器传输环节的静态特征，分析不同能源网能量传输过程的动态变化规律，在稳态混合潮流分析的基础上，针对不同能源网传输过程中的能量损失，以CHP和GB机组实时出力量为自变量建立多目标优化模型。

下面仅给出天然气网和热网潮流计算模型，省略电网潮流计算过程。

（1）含压缩机的天然气网络模型。

一般天然气管道稳态流量fk由管道特性和节点压强决定：

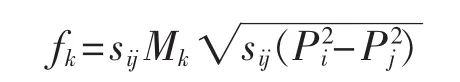
其中，Mk为常数，由管道参数、环境温度和工质决定，计算方法详见文献［18-19］；sij为该管道流量，正方向为节点i流向节点j；Pi为天然气网节点i的压强。

天然气潮流连续性方程为M=Agf，其中M为各个天然气节点流出流量，Ag为去掉压缩机后的天然气节点支路关联矩阵，f为天然气管道流出流量。

一般燃气直驱式压缩机工作在定输出压强的模式，建立压缩机工作模型，图4中fc、fo、fin分别为压缩机天然气消耗量、流出流量和流入流量。

其中，kc为气体压缩比，初始值设为已知输出压强与p点压强比值；qgas为天然气热值；Tgas为天然气热值；a为多变指数；Moq、Mpq分别为压缩机出口和入口的管道常数。定义计算误差为Δf=fin-fc-fo，如不满足给定精度，则修改气体压缩比kc=Pout／Pp和p、q节点等效流出流量，再次计算，直到计算误差在可接受的范围内。

图4 天然气压缩机工作原理示意图Fig.4 Schematic diagram of natural gas compressor

（2）热力系统模型。

（4）管理。小湖泊精养小龙虾，由于放养密度大，仅依靠天然生物饵料不能满足鱼类、小龙虾类生长的需要，因此应适当进行投饲施肥。在日常的管理工作中，要重点做好以下几点工作：一是改善水域条件，提高水体肥力，方法是可以通过人工施肥来提高湖泊水体肥力，常用的是无机肥料，每亩面积可施用尿素1.5～2.5kg，碳酸氢铵2.0～3.0kg，效果很好；二是抓好鱼种配套、苗种放养、投饲施肥、防逃防病、合理捕捞等技术措施。

热力系统模型包括4个方程：流量连续性方程式（22），即节点注入流量等于流出流量；节点热输出功率计算公式（式（23））；管道热损耗计算式（式（24）），根据管道参数、环境温度Ta和管道起始点温度Tstart求管道终点温度Tend；回水管道多条支路热水混合后的水温计算公式（式（25））。

其中，Ah为热力系统节点支路关联矩阵；m为管道流量向量；mq为负荷消耗的热流量向量；Φi为某节点输出的热功率，Φi为正时表示该节点向热网供给热能；Cp为水的比热容；Ts，i、To，i分别为节点 i出水温度和进水温度；mq，i、mj分别为节点 i流出量流量和管道j的热流量；热损耗计算式（24）中的管道参数包括管道长度l和热传导系数λh；回热温度Tr为从负荷节点流出的热水在管道汇合节点处与其他管道热水混合后的温度；min和Tin分别为流入流量和温度。

3 模糊综合决策方法

机组优化分配以热负荷节点温度偏移即热损耗、电网线路损耗和天然气网压强偏移作为热电气网络的评价指标，由优化算法得出这3个指标的一系列Pareto前沿作为非劣解集合，ICES优化中多能网的优化目标众多且很难统一量化到相同的量纲，面对目标数量较多时利用理想模糊决策方法辅助决策过程。

先在Pareto前沿中按比例选取离散解作为备选方案。专家对方案不同的决断构成的集合作为评语集，用三角模糊数［20］来表征专家对目标的主观权重的评价指标度量，模糊数的取值范围为［0，1］，模糊数越大表示该评价指标越重要。若由n位专家给J个指标作评价，第i位专家给第j位指标的模糊权重为 rij，对指标 j而言评判矩阵记为 Rj=［r1j，r2j，…，rnj］。模糊综合评判矩阵记为R。

给每位专家设定相同权重 e＝1／J×［1，1，…，1］T，热损耗、电损耗和天然气网络压强偏移这3个指标的权重为 w＝e·R。

在确定热、电、气3个指标权重后，具体的决策步骤如下。

a.对所有指标k个Pareto前沿非劣解的3个指标数据规范化。应用标准0-1变换，本文中3个指标均为成本属性，对于第i个非劣解的第j个指标aij，按照下式进行变换。

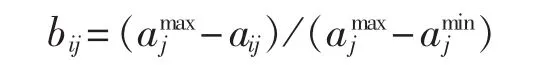
b.形成加权规范矩阵 Cij＝ （cij）k×J，cij＝wj×bij。

d.计算各方案到正负理想解的距离。

方案i到正理想解和负理想解的距离分别为：

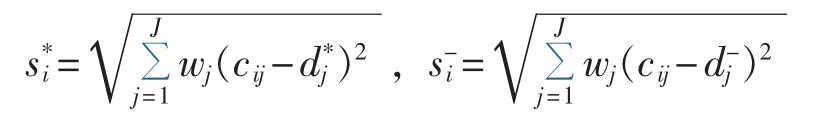
e.计算各个方案的综合评价指数

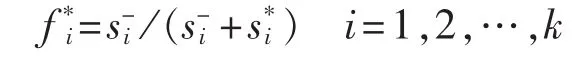
4 算例分析

本文选取商业区作为研究对象，配网额定电压为10kV。以一天24h为运行周期，1h为一次优化调整周期。该区域1 d冬季典型热、电负荷曲线和实时电价预测曲线如图5所示。算例拓扑结构如图6所示，图中GP、HP和EP分别表示天然气网、热网和电力网的节点。

图5 日热电负荷预测与实时电价典型图Fig.5 Typical diagram of predicted daily thermal and electric power loads and real-time tariffs

图6 ICES算例网络拓扑示意图Fig.6 Network topology of ICES example

发电供热和能量转化效率以及模型中的其他具体参数见表1。假设电网各个节点在同一时间电负荷相同，且功率因数均为0.85，热网中各个节点热功率在同一时间之比为定值，CHP和GB供热出口温度设为100℃。

表1 模型关键参数表Table 1 Key parameters of model

为验证模型有效性，构建4种运行模式对运行成本、用能效率以及热电气网三网设定的3个运行指标进行比较，具体4种模式如下。

模式1：CHP机组均工作于以热定电FTL（Following the Thermal Load）模式，设定热电比VCHP为定值2，CHP1与CHP2机组输出功率相同。

模式2：CHP机组工作于以电定热FEL（Following the Electrical Load）模式，其他设定同模式1。

模式3：CHP机组工作于热电比可调模式，运用双层优化模型，每小时滚动优化天然气用能比V（t）与热电联产热电比VCHP，CHP1与CHP2机组输出功率相同。

模式4：CHP1与CHP2机组输出功率可调且由机组优化分配模型优化得出，其他设定同模式3。

本文采用自适应遗传算法求解模式3、4中非线性双层非线性优化模型，算法收敛性完备证明详见文献［21］，优化处理后 24 h 的 V（t）和 VCHP（t）分别见图 7、图 8。

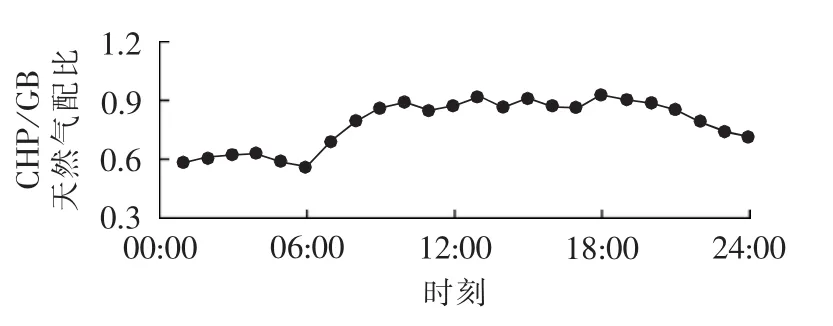
图7 模式3、4下CHP／GB天然气优化配比Fig.7 Optimal natural gas ratio of CHP to GB for Mode 3 and 4

图8 多模运行状态热电比对比图Fig.8 Comparison of thermal-electric ratio among different operating modes

将模式3、4优化后的综合用能成本和用能效率与模式 1（FTL）、模式 2（FEL）进行比较，得到图9、图 10。

由图9可知，优化后的综合用能成本和单位用能成本均低于传统以热定电以及以电定热的工作模式；由于上层优化给出的V（t）与调度模式1、2下的V（t）不同，用能效率在某些时段并不是所有模式中最优的，但由图10可知，虽然在某些时刻优化后的用能效率不如模式2，但是在用能成本最优的前提下，模式3、4可通过能效优化层寻优，使用能效率保持较优水平。

图9 多模运行区域总用能费用对比图Fig.9 Comparison of total energy cost among different operating modes

图10 多模运行总用能效率对比图Fig.10 Comparison of total energy efficiency among different operating modes

对于模式4中CHP机组的优化，根据搜索算法得到各个时刻热损耗、电网线路损耗和天然气网压强偏移者3个目标下的10个Pareto前沿非劣解，以12∶00为例，得到Pareto非劣解如图11所示。

图11 多目标优化Pareto前端非劣解图Fig.11 Curve of Pareto front-end non-inferior solution by multi-objective optimization

考虑专家对多个目标的评价，对投资方、电网运行部门、环保部门和园区管理部门调查得出的专家评价结果如表2所示。在非劣解集合中等间距地选取10个方案，并采用本文第3节提出的模糊综合决策方法求解相应的贴合度。

表2 非劣解多目标参数及评价结果表Table 2 Multi-objective parameters and evaluation results of non-inferior solutions

推荐贴合度较高的方案4，此时2台CHP机组承担的功率占比为1.33∶1。对24 h综合决策后的优化结果见图12模式4。

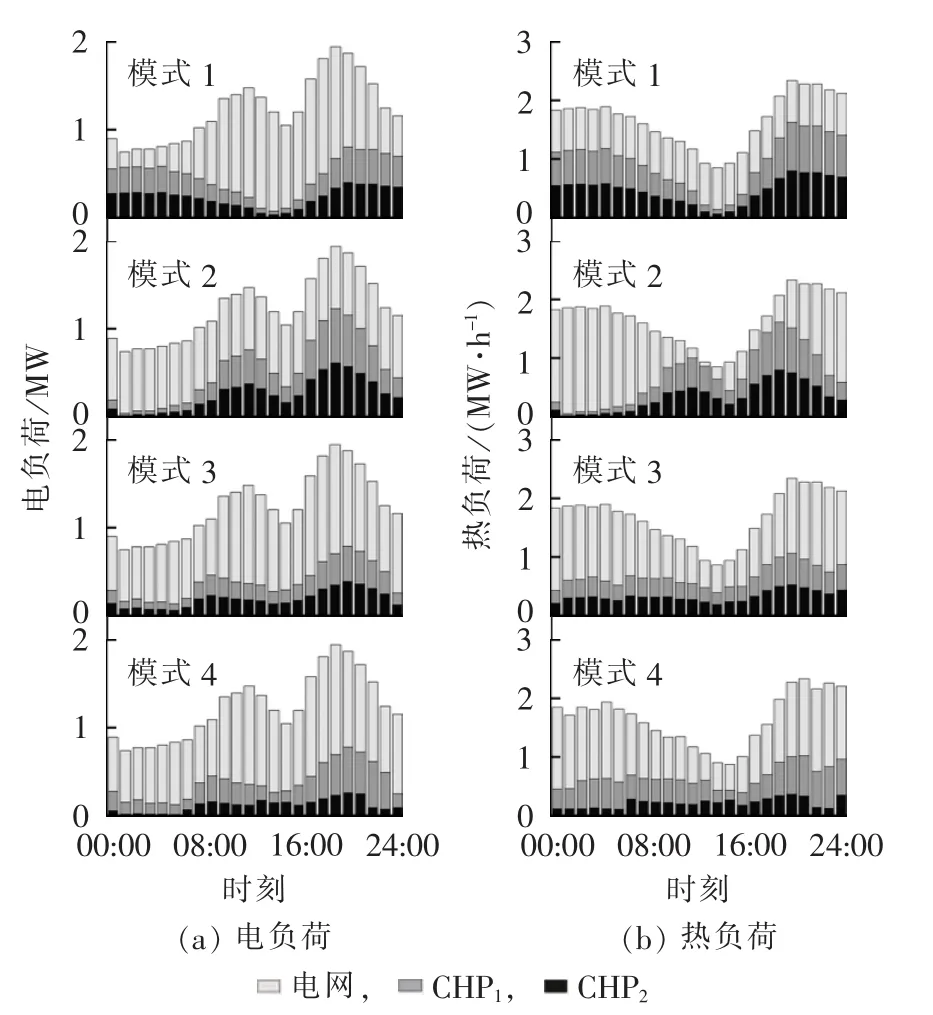
图12 多模运行方式电热功率图Fig.12 Thermal and electric power diagrams of four operating modes

将机组优化与前面3种CHP机组承担相同功率的调度方法作比较，可知机组优化层可以在设定指标权重的基础上选贴合度较高的CHP机组组合方案，优化热电气三网的运行状态。

图12为模式1—4各个时段电功率与热功率的出力占比，其中，电功率考虑电网处购电和CHP发电部分的电能，热功率包括GB以及2台CHP余热回收部分的热能。从优化结果来看，基于EH分层优化结果对于热电负荷波动的鲁棒性较强，通过电网、GB和CHP多个能源转换单元有机协调整合，热电负荷波动不仅由CHP机组单方面承担，CHP机组热电功率随时间的波动较小，运行态势较平稳。

5 结论

本文提出了一套适用于区域ICES的日前调度分层设计构架和基于EH的实时优化方法。综合考虑补燃机组热电比可调、综合需求侧响应以及能源连接器的动态过程，提出了针对ICES用能成本和用能效率的双层优化模型，并全面考虑了动态能源连接器的运行状态，分析了电网、GB和CHP机组的组合优化问题。最后以一个实际的电热气ICES为算例，结合广州工业园区项目部分调研结果和历史运行数据检验方法的有效性。研究结果表明：相比于传统的运行方式，基于EH的ICES分层优化模型对于多能耦合系统有清晰的理论描述，在降低用能成本、提高整体用能效率、优化电热气系统运行状态方面有较好的实用效果，适用于实行实时电价或峰谷电价且运行方法灵活可调的中小型区域综合能源优化调度。

参考文献：

［1］于慎航，孙莹，牛晓娜，等.基于分布式可再生能源发电的能源互联网系统［J］. 电力自动化设备，2010，30（5）：104-108.YU Shenhang，SUN Ying，NIU Xiaona，et al.Energy-based internet system based on distributed renewable energy［J］.Electric Power Automation Equipment，2010，30（5）：104-108.

［2］王伟亮，王丹，贾宏杰，等.能源互联网背景下的典型区域综合能源系统稳态分析研究综述［J］. 中国电机工程学报，2016，36（12）：3292-3305.WANG Weiliang，WANG Dan，JIA Hongjie，et al.A survey of steady state analysis of typical regional integrated energy systems in the context of energy internet［J］.Proceedings of the CSEE，2016，36（12）：3292-3305.

［3］张勇军，陈泽兴，蔡泽祥，等.新一代信息能源系统：能源互联网［J］. 电力自动化设备，2016，36（9）：1-7.ZHANG Yongjun，CHEN Zexing，CAI Zexiang，et al.New generation information energy system：energy internet［J］.Electric Power Automation Equipment，2016，36（9）：1-7.

［4］GEIDL M，KOEPPEL G，FAVRE-PERROD P，et al.Energy hubs for the future［J］.IEEE Power and Energy Magazine，2007，5（1）：24-30.

［5］GEIDL M，ANDERSSON G.A modeling and optimization approach for multiple energy carrier power flow［C］∥Power Tech，2005 IEEE. ［S.l.］：IEEE，2005：1-7.

［6］余晓丹，徐宪东，陈硕翼，等.综合能源系统与能源互联网简述［J］. 电工技术学报，2016，31（1）：1-13.YU Xiaodan，XU Xiandong，CHEN Shuoyi，et al.Brief introduction of integrated energy system and energy［J］.Transactions of China Electrotechnical Society，2016，31（1）：1-13.

［7］LIU X，WU J，JENKINS N，et al.Combined analysis of electricity and heat networks［J］.Applied Energy，2016，162：1238-1250.

［8］潘昭光，孙宏斌，郭庆来.面向能源互联网的多能流静态安全分析方法［J］. 电网技术，2016，40（6）：1627-1634.PAN Zhaoguang，SUN Hongbin，GUO Qinglai.Static energy analysis method for multi-energy flow oriented to energy internet［J］.Power System Technology，2016，40（6）：1627-1634.

［9］徐宪东，贾宏杰，靳小龙，等.区域综合能源系统电／气／热混合潮流算法研究［J］. 中国电机工程学报，2015，35（14）：3634-3642.XU Xiandong，JIA Hongjie，JIN Xiaolong，et al.Study on hybrid power flow algorithm of electricity ／gas／heat in regional integrated energy system［J］.Transactions of China Electrotechnical Society，2015，35（14）：3634-3642.

［10］XU X，JIA H，CHIANG H D，et al.Dynamic modeling and interaction of hybrid natural gas and electricity supply system in microgrid［J］.IEEE Transactions on Power Systems，2015，30（3）：1212-1221.

［11］王英瑞，曾博，郭经，等.电-热-气综合能源系统多能流计算方法［J］. 电网技术，2016，40（10）：2942-2950.WANG Yingrui，ZENG Bo，GUO Jing，et al.Calculation method of multi-energy flow in electro-thermal-gas integrated energy system［J］.Power System Technology，2016，40（10）：2942-2950.

［12］KAMALINIA S，WU L，SHAHIDEHPOUR M.Stochastic midterm coordination of hydro and natural gas flexibilities for wind energy integration［J］.IEEE Transactions on Power Systems，2014，5（4）：1070-1079

［13］XU X，JIN X，JIA H，et al.Hierarchical management for integrated community energy systems［J］.Applied Energy，2015，160：231-243.

［14］ZHANG X，SHAHIDEHPOUR M，ALABDULWAHAB A，et al.Optimal expansion planning of energy hub with multiple energy infrastructures［J］.IEEE Transactions on Smart Grid，2015，6（5）：2302-2311.

［15］顾伟，吴志，王锐.考虑污染气体排放的热电联供型微电网多目标运行优化［J］. 电力系统自动化，2012，36（14）：177-185.GU Wei，WU Zhi，WANG Rui.Multi-objective operation optimization of cogeneration power grid considering pollutant gas emission［J］.Automation of Electric Power Systems，2012，36（14）：177-185.

［16］李朋，臧向东，刘聿拯，等.分布式热电联产中热电比的确定［J］.热电技术，2005，18（4）：43-46.LI Peng，ZANG Xiangdong，LIU Yuzheng，et al.Determination of thermoelectric ratio in distributed combined heat and power［J］.Thermal Power Generation Technology，2005，18（4）：43-46.

［17］贾飞.解非线性双层规划的算法研究［D］.西安：西安电子科技大学，2014.JIA Fei.Study on algorithm of nonlinear bilevel programming［D］.Xi’an：Xi’an University of Electronic Science and Technology，2014.

［18］AN S，LI Q，GEDRA T W.Natural gas and electricity optimal power flow［C］∥Transmission and Distribution Conference and Exposition，2003 IEEE PES. ［S.l.］：IEEE，2003：138-143.

［19］江茂泽，徐羽镗，王寿喜，等.输配气管网的模拟与分析［M］.北京：石油工业出版社，1995：205-219.

［20］管霖，陈鹏，唐宗顺，等.考虑冷热电存储的区域综合能源站优化设计方法［J］. 电网技术，2016，40（10）：2934-2941.GUAN Lin，CHEN Peng，TANG Zongshun，et al.Optimized design method of integrated energy station considering cold and thermoelectric storage［J］.Power System Technology，2016，40（10）：2934-2941.

［21］李和成.非线性双层规划问题的遗传算法研究［D］.西安：西安电子科技大学，2009.LI Hecheng.Research on geneticalgorithmsfornonlieaner bilevel programming program［D］.Xi’an：Xi’an University of Electronic Science and Technology，2009.