杆塔刚性法兰加劲肋在轴力作用下的荷载分配

杨隆宇，施菁华

(中国电力工程顾问集团 华北电力设计院有限公司，北京 100120)

杆塔刚性法兰加劲肋在轴力作用下的荷载分配

杨隆宇，施菁华

(中国电力工程顾问集团 华北电力设计院有限公司，北京 100120)

钢管构件节点处拉力分别通过加劲肋和法兰盘环形焊缝传递，二者传力分配对加劲肋承载力计算有较大影响。现有研究对传力比例是固定还是动态变化、二者分配比例都有不同理解；同时，规范中给出的计算方法存在与实际明显不符之处。由于刚性法兰加劲肋设置的特点，在试验中不易提取到环形焊缝及加劲肋端部传递的轴向荷载的准确值，因此，建立6个不同螺栓数的包含钢管、法兰、螺栓、加劲肋、焊缝的完整刚性法兰模型(钢管分别为φ219×8、φ506×8)，根据节点实际受力情况分别设置数百个接触对的接触行为和参数。将模型求解结果与现有节点试验结果对比，表明模型有较好精度；通过加劲肋传递的内力比例随参数Ly/Lx变化；现有规范中给出系数α偏保守。结合模型计算结果，考虑刚性法兰工程实际并保留一定裕度，给出简化的刚性法兰加劲肋计算公式，为设计提供参考。

特高压；刚性法兰加劲肋；有限元；荷载分配；简化设计

0 引言

与特高压线路杆塔建设的相关研究在我国不断推进[1-5]。钢管作为常用截面，其节点处用法兰和螺栓连接，是重要的受力部件。现有对刚性法兰的研究多针对法兰盘，对加劲肋的分析较少[6-7]。

在受拉时，由于螺栓拉力通过2个路径传递，因此，加劲肋所传递拉力的比例是很重要的输入参数。现有研究对此只有不同认识，文献[8]中给出的传力比例随Ly/Lx不同而变化，认为最大时90%以上拉力都通过加劲肋传递；文献[2]146通过分析得出加劲肋传递约40%拉力的结论。

由于刚性法兰构造复杂，试验中不易精确测得通过加劲肋和钢管传递的内力大小，因此通常通过建立有限元模型的方法研究其受力情况。对节点构件的简化方式的不同理解是造成各文献所得结论不统一的另一个原因。分析过程中常利用构件对称性只建立局部模型[9-12]，在对称面上人为设定的边界条件不能很好地反映钢管、法兰、螺栓、加劲肋、焊缝等的相互作用，最终求解的应力和变形与实际情况存在一定不同；另一个常用的简化方式是用SHELL单元代替SOLID单元，这样能减少单元数量并保证计算结果准确性，也便于提取内力，但是法兰节点中，钢管、法兰、加劲肋厚度的量级相差较小，如果个别部件采用无厚度的SHELL单元，这会对其他部件几何尺寸产生较大影响。

针对上述不足，本次采用高阶SOLID单元按实际尺寸建立完整的包含接触行为的精细化有限元模型(包含法兰、螺栓、钢管、焊缝、加劲肋等部件)，考虑不同Ly/Lx的影响，探讨轴向拉力作用下加劲肋传力状态；分析并修正现有计算方法中不合理的设定，得到适用于加劲肋计算的简化公式。

1 有限元分析

为研究不同Ly/Lx、螺栓个数、法兰盘厚度时刚性法兰传力路径及对加劲肋受力的影响，共计算6种尺寸的有限元模型。钢管规格分别为φ219×8、φ506×8，法兰、钢管、加劲肋为Q345钢材，弹性模量E=2.06e11 Pa，泊松比0.3，螺栓采用8.8级M24。根据Q345材性试验结果，钢材本构关系采用多折线模型。之前研究受拉刚性法兰经常利用对称性采用简化模型，会对最终计算结果产生影响。为解决这一问题，本次建立完整的刚性法兰计算节点。刚性法兰计算模型如图1，模型参数见表1。

节点一端固定，一端施加拉力；螺栓、焊缝、加劲肋、钢管、法兰等相互之间接触行为、参数等根据实际情况设定，更具模型复杂程度不同，最多需设置数百个接触对。

图1 刚性法兰计算模型

模型细部网格划分如图2所示。模型中综合应用高阶SOLID单元：对规则实体采用六面体单元；对形状复杂、不规则的实体将其退化为四面体单元。由于本次加劲肋与钢管、法兰盘的厚度相差不大，且法兰盘厚度还影响螺栓杆长、对其变形有较大影响，因此各部位均以实体模型建立，通过加密网格来保证计算精度。

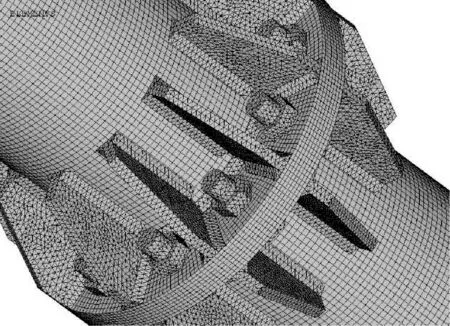
图2 模型网格划分

G13模型求解后如图3所示，提取到的加劲肋截面应力如图4所示。模型变形趋势和等效应力分布规律符合力学计算模型。应力集中区域、破坏过程与文献[2]148中刚性法兰节点受拉试验结果基本一致。

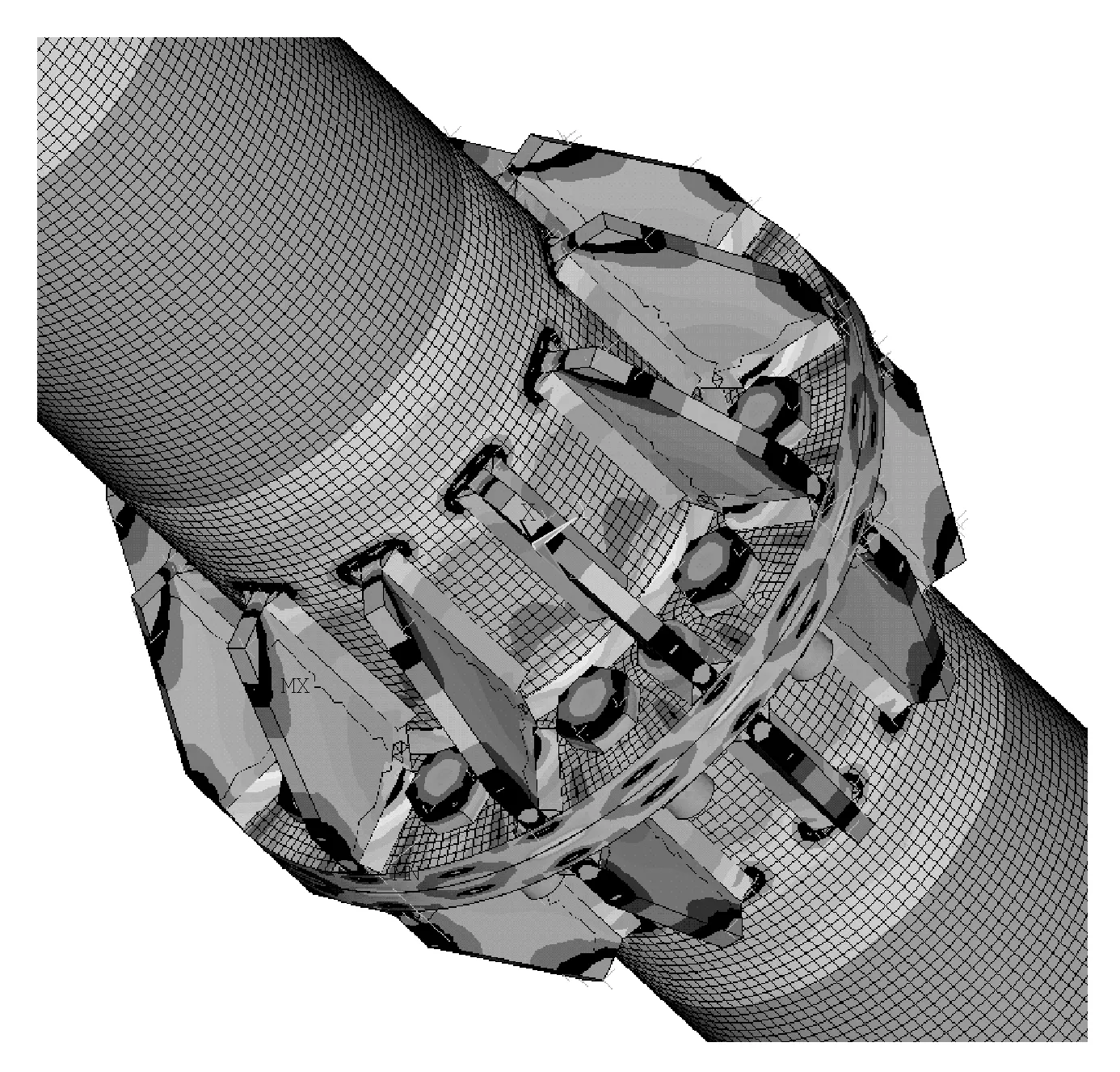
图3 模型等效应力图

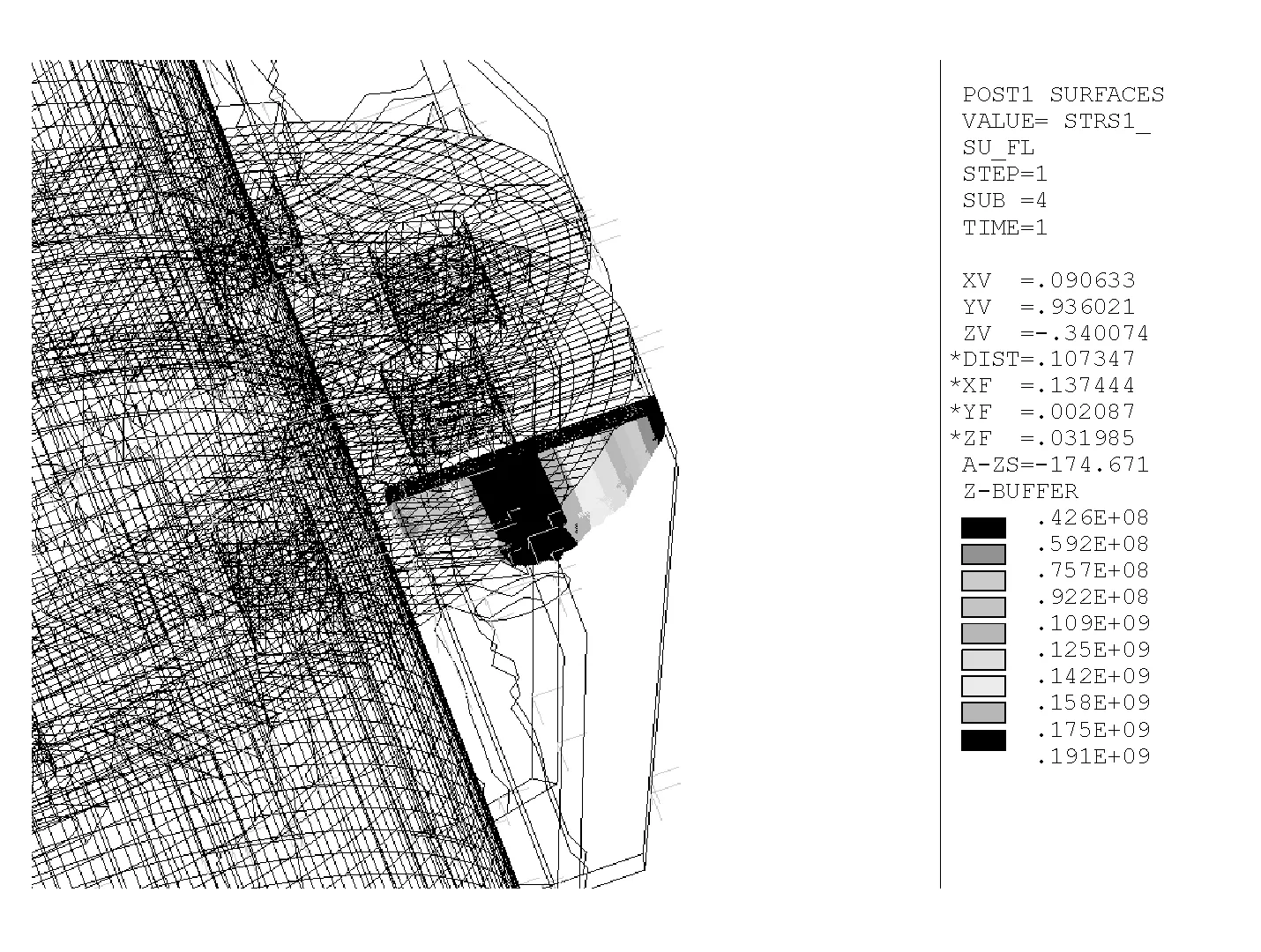
图4 加劲肋截面内力

2 加劲肋传力比

刚性法兰中螺栓拉力主要通过2个路径传递到钢管：通过法兰和钢管之间环形焊缝传递(路径I)，通过加劲肋传递(路径II)，如图5所示。

图5 刚性法兰节点传力路径

本次模型计算所得2个路径的传力比例列于图6中。

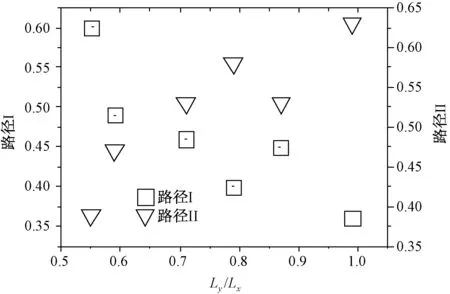
图6 传力路径比较

本次计算的6种模型，通过加劲肋传递的力与通过环形焊缝传递的力之和与施加的外荷载相符，计算模型有足够的精度。当Ly/Lx增加时路径II传力比例整体上升，路径I逐渐下降，表明2个传力路径之间的分配比例是动态变化的，加劲肋传递的力在40%～60%范围。

文献[8]24中根据不同Ly/Lx给出不同的α值和本次有限元计算得到的α值的对比如图7所示。

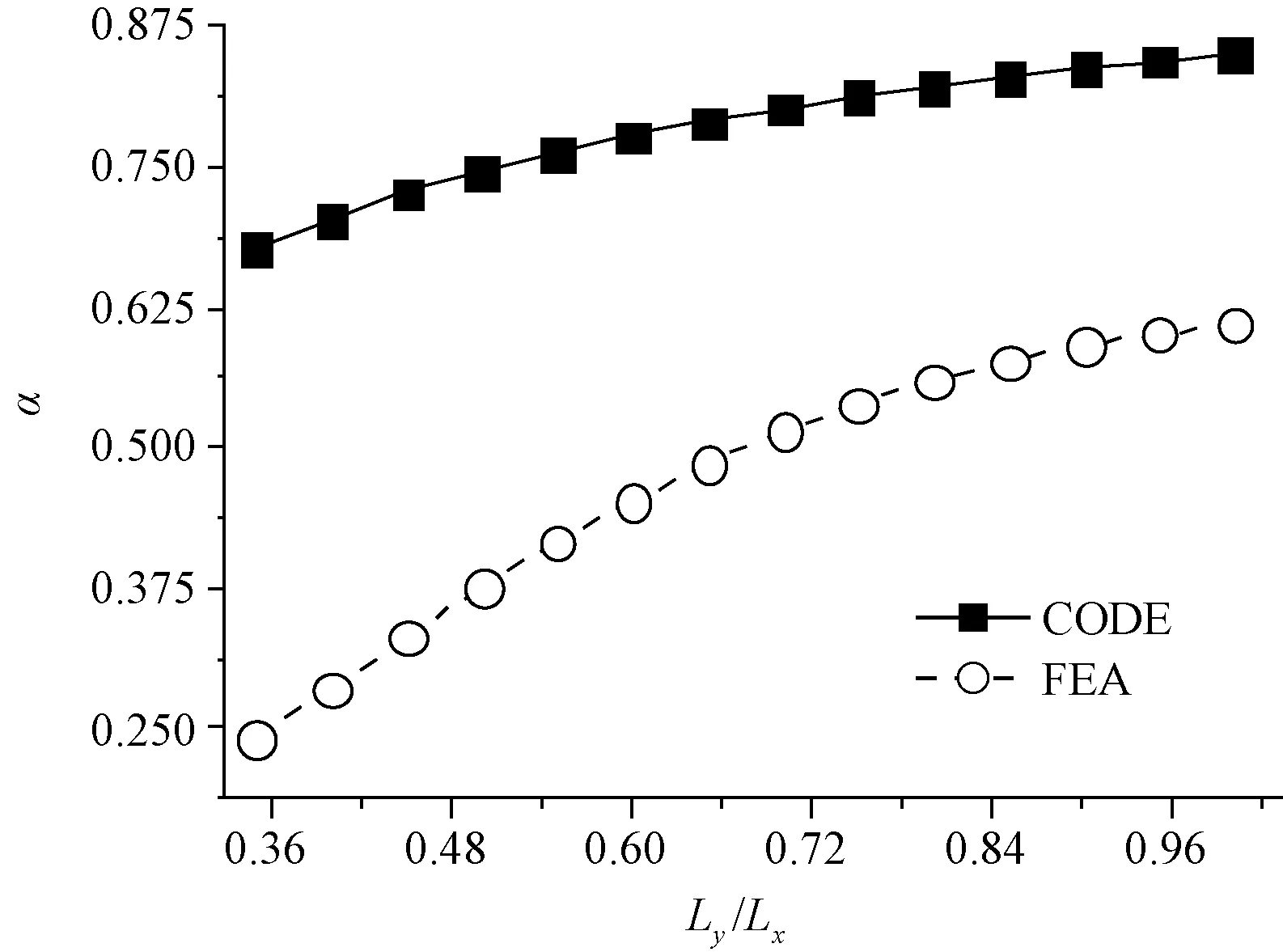
图7 加劲肋传力比α

图7中CODE曲线为文献[8]40曲线，FEA曲线为有限元计算后拟合曲线。CODE曲线整体偏高(平均比FEA曲线高70%)，当Ly/Lx增大后二者差值趋于稳定，大约为40%左右。结果表明文献[8]40给出的加劲肋的α值偏保守。

3 建议的加劲肋计算公式

加劲肋计算简图如图8所示。文献[8]40中对加劲肋的计算给出下列公式：

(1)

(2)

(3)

(4)

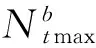
图8 加劲肋计算简图

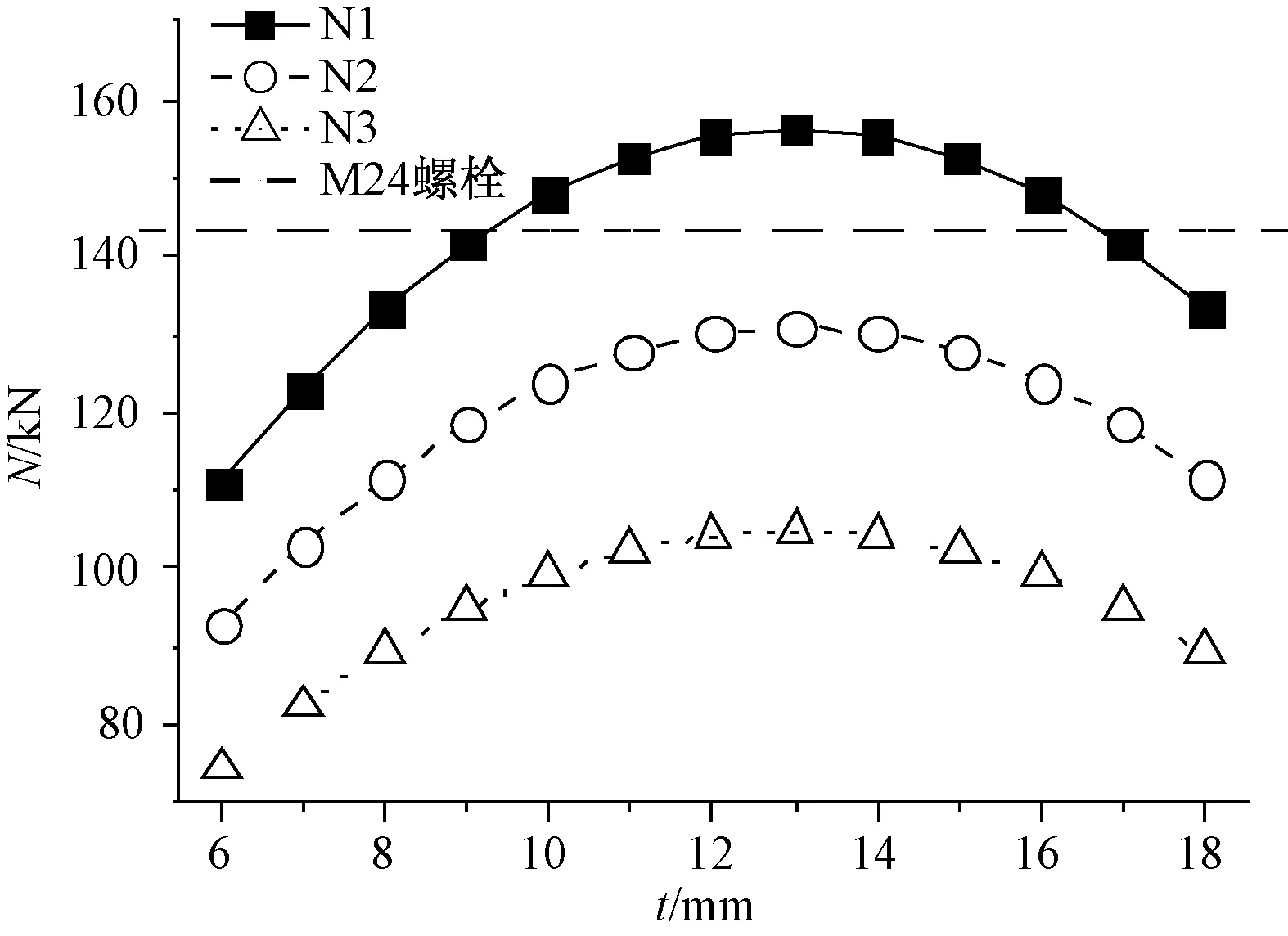
图9 不同加劲肋厚度对应的承载力

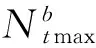
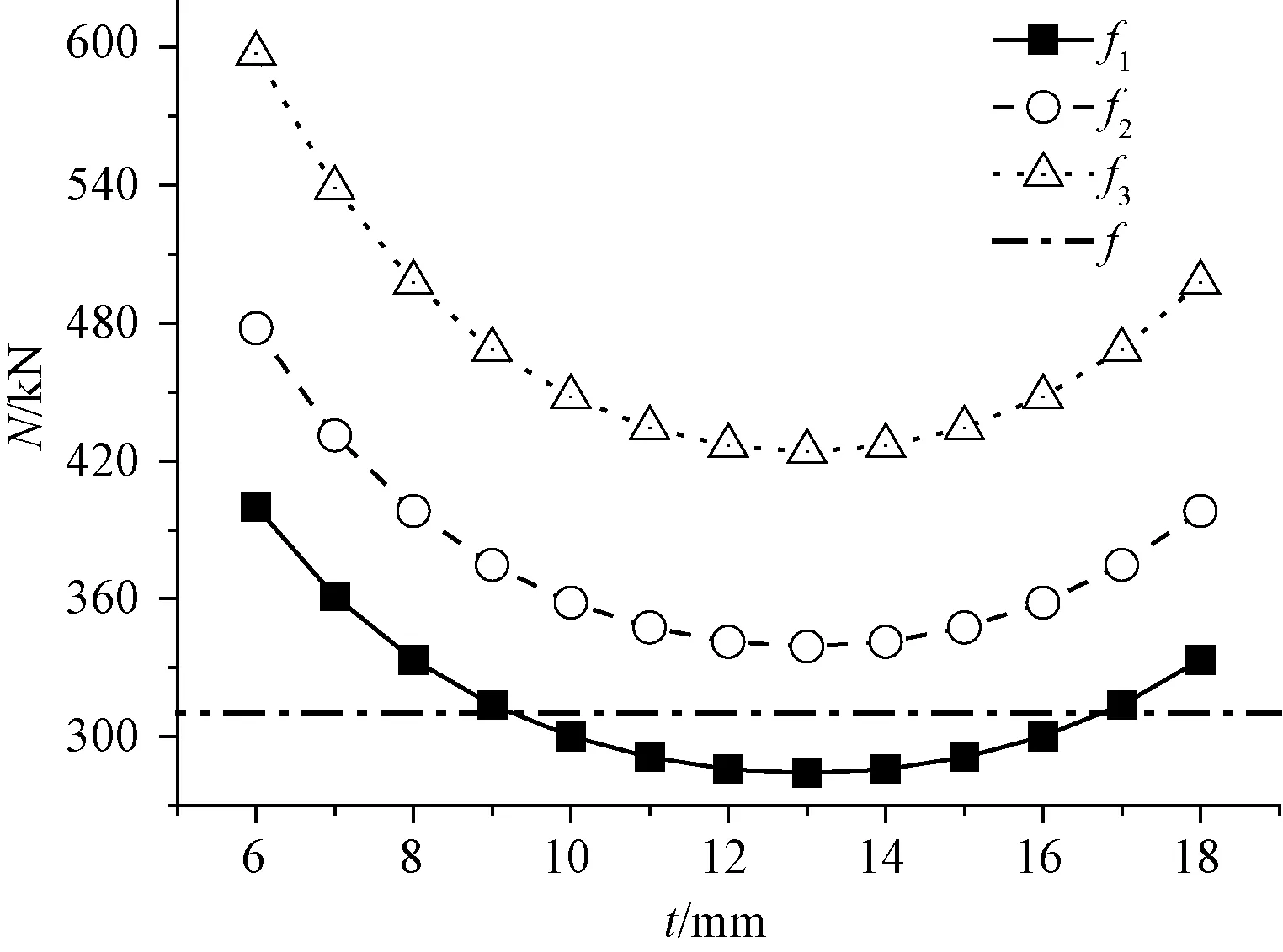
图10 水平焊缝应力

图10中曲线f表示焊缝的应力设计值，f1～f3为不同α时验算得到的焊缝应力。可以看出，仅当α值很小时部分厚度的加劲肋的焊缝低于应力限值，其α加大后即便加大的加劲肋厚度均无法满足要求。这与实际情况也是不符的，表明公式(4)并不能很好地应用于加劲肋的设计、验算。

出现这种情况的原因是公式(4)中计算焊缝截面时在加劲肋边长方向加入了一项“2t”，使二者关系从线性变成了抛物线形式。由于该部位主要承受法向拉力，观察公式(4)之后很自然的想法是原文中参数“2t”的加入是来自文献[7]55中对角焊缝计算长度的说明：要求每条焊缝实际长度减去2倍hf(hf为焊脚尺寸)。由于公式(4)中按对接焊缝考虑，“2hf”就变成“2t”。

为调和上述不合理，考虑文献[8]40给出的加劲肋的α偏保守，根据输电塔中刚性法兰实际情况，并考虑一定安全裕度，建议将公式(4)改为：

(5)

式中：tg为钢管壁厚。

采用公式(5)计算常用Ly/Lx范围加劲肋承载力与M24螺栓对比如图11。

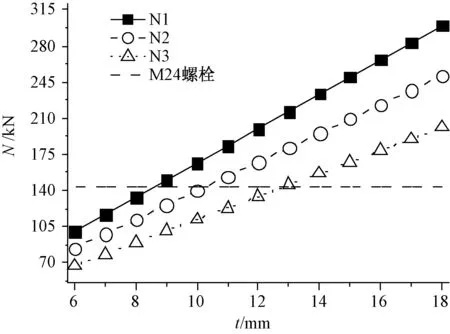
图11 建议的加劲肋计算方法

4 结论

与现有刚性节点试验对比可知，建立的完整刚性法兰模型具有较好精度，并有效解决了节点试验提取内力困难的问题。通过对文献[8]40计算方法的分析和有限元计算，得到下列结论：

(1)刚性法兰节点中通过加劲肋传递的内力占比不是一成不变的，它随节点几何参数Ly/Lx非线性变化，与文献[8]40描述的情况比较接近。

(2)在Ly/Lx=0.3～1.0范围时，文献[8]40中加劲肋传力比例α=0.67～0.85，其值比有限元计算结果平均高70%，当Ly/Lx增大后二者差值虽趋于稳定，依然相差约40%。文献[8]40明显偏保守。考虑刚性法兰节点的实际情况，α可适当放宽。

(3)文献[8]40给出的加劲肋B边计算公式存在不合理之处，该公式不能很好地用于加劲肋设计、验算。根据有限元计算结果和该公式设计思路，给出建议的简化公式，可为工程设计作参考。

[1] 杨隆宇. 考虑多种应力的组合截面填板承载力研究[J]. 电力科学与工程，2014，30(8)：33-27．

[2] 王宇强，张大长，李步辉，等. 圆管刚性法兰加劲肋角焊缝受力特性及强度计算理论[J]. 工程力学，2015，32(7)：143-148.

[3] 王华娟, 王峰. 输电线路钢管杆法兰连接设计[J]. 山东电力技术, 2015, 42(6): 62-65.

[4] 杨隆宇. 高强双角钢十字截面构件承载力折减系数[J]. 电力科学与工程，2015，31(6)：74-78.

[5] 王宇强. 新型圆钢管刚性法兰抗弯承载力试验及理论分析[D]. 南京: 南京工业大学, 2014: 1-8.

[6] GB 50017-2003，钢结构设计规范[S].北京：中国计划出版社，2003.

[7] DL/T 5154-2012，架空送电线路杆塔结构设计技术规定[S]. 北京：中国电力出版社，2012.

[8] DL/T 5254-2010. 架空输电线路钢管塔设计技术规定[S].北京：中国电力出版社，2010.

[9] 王宇强, 张大长, 李步辉，等. 圆管刚性法兰加劲肋角焊缝受力特性及强度计算理论[J]. 工程力学，2015，32(7)：143-148.

[10] 王孟，陈学辉. 高压输电钢管塔柔性法兰承载性能的有限元分析[J]. 华北电力大学学报(自然科学版)，2015，42(2)：66-71.

[11] 陈学辉. 特高压钢管塔用柔性法兰结构强度分析[D]. 北京：华北电力大学，2015.

[12] WANG X Y，LUO Y F，QIANG X H，et al. Review on high strength steel bolted end-plate connections[C]. Applied Mechanics & Materials, 2015: 265-273.

Load Allocation for Rigid Flange Stiffener Connection Used in UHV Transmission Tower under Axial Force

YANG Longyu，SHI Jinghua

(North China Power Engineering Co. Ltd. of China Power Engineering Consulting Group，Beijing 100120，China)

For circle hollow section members, there are two components for the transmission of axial load: the circumferential weld and flange stiffener. The allocation proportion of axial load has great influence on the design of stiffener. It is controversial that whether the allocation proportion is dynamic; and meanwhile, the share of stiffener is quite different in recent studies. The calculation formula of existing design method does not agree with the fact. Due to the complexity of joint structure, it is hard to measure the accurate stress of the force transmission whole components (stiffener and circumferential weld). The finite element models of 6 rigid flange stiffener joints are established which contain components such as pipes(φ219×8,φ506×8), flanges, bolts, stiffeners, and welding seams. Hundreds of contact pairs are defined by contact behavior and parameters for these FE models. The results show: data obtained after solution phase is in good precision comparing with available experiment; parameter α varies withLy/Lx; the existing design method provides a rather conservative result. Taking consideration of FEA results and engineering status, the proposed formula can be an effective solution for flange stiffener connection design.

UHV；stiffener of rigid flange；FEA；load allocation；simplified design

10.3969/j.ISSN.1672-0792.2017.04.013

2016-12-22。

TU392.6

A

1672-0792(2017)04-0069-05

杨隆宇(1981-)，男，博士，高级工程师，研究方向为输电线路杆塔设计、钢结构稳定。