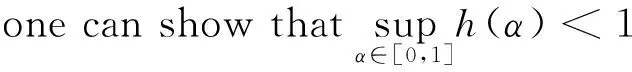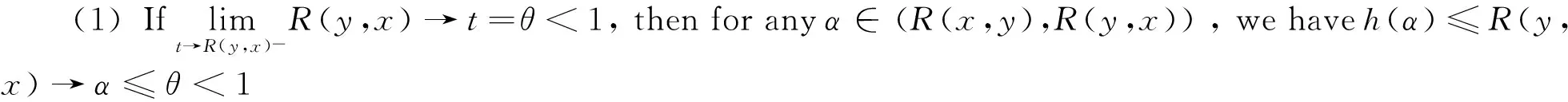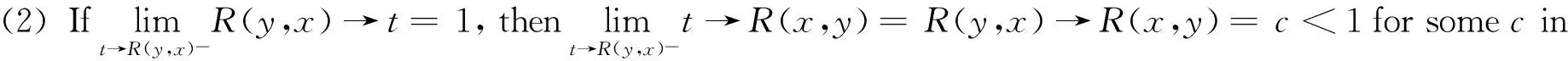The Degree of the Symmetry of Fuzzy Relations①
Dan Ye-xing
(Department of Mathematics, Sichuan University, Chengdu 610064, China)
The Degree of the Symmetry of Fuzzy Relations①
Dan Ye-xing
(Department of Mathematics, Sichuan University, Chengdu 610064, China)
In this paper, the degree of the symmetry of fuzzy relations is investigated based on the fuzzy equality of fuzzy relations.
fuzzy relation, degree of the symmetry, symmetric fuzzy relation, fuzzy equality
1 Introduction
Let & be a left continuous t-norm. There is a natural fuzzy equality on the fuzzy powerset [0,1]Xgivenby


GivenafuzzyrelationRonasetX,itissymmetricif,andonlyifR=Rop,whereRopisthedualityofR.However,whenRisnotsymmetric,wecantalkaboutthedegreeofthatRandRopareequal.ThedegreecanberegardedasthedegreeofthesymmetryofR[3, 4].
NoticethatafuzzyrelationRonasetXissymmetricifandonlyifthereisasymmetricfuzzyrelation,sayS,suchthatR=S.Ifwehavethefuzzyequalityonfuzzyrelationsinsteadofthecrispequality,wegetanotherapproachtodefinethedegreeofthesymmetryoffuzzyrelations(seeDefinition1).
In this paper, we will study the degree of the symmetry of fuzzy relations defined by the second approach. The contents are arranged as follows. In Section 2, we recall some basic notions of left continuous t-norms and fuzzy equalities. In Section 3, the main results are proved.
2 Preliminaries
First, we recall some basic notions of triangular norms and fuzzy equivalences[1,2]. A left continuous triangular norm (t-norm for short) is a binary operation & on the interval [0,1] such that ([0,1], &) is a commutitative monoid with 1 being the unit, and for eachxin [0,1],x&(-):[0,1][0,1]hasarightadjointx→(-):[0,1][0,1]inthesensethatforally,zin [0,1]
x&y≤z⟺y≤x→z.
Aleftcontinuoust-norm&iscontinuousif&isacontinuousfunction.
Example 1 (Klement, Mesiar and Pap[1]) Some basic left continuous t-norms on [0,1] are listed here. The first three are continuous but the fourth not.
(1)The Gödel t-norm &M:x&My=x∧y.Thecorrespondingresiduationandbiresiduationisgivenby
(2)Theproductt-norm&P:x&Py=x·y.Thecorrespondingresiduationandbiresiduationisgivenby
(3)TheLukasiewicat-norm&L:x&Ly=(x+y-1)∨0.Thecorrespondingresiduationandbiresiduationisgivenby


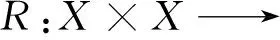
AfuzzyrelationEonXiscalledafuzzyequalityifitsatisfiesthat(1)E(x,y)=1 iffx=y, (2)E(x,y)=E(y,x),(3)E(x,y)&E(y,z)≤E(x,z) for allx,y,zinX.ThevalueofE(x,y) is often interpreted as the degree of the thatxequals toyin the setX.
Example 2 (1)Given a t-norm &, the operationx↔yontheunitintervalgivesanaturalfuzzyequality
E(x,y)=x↔y=(x→y)∧(y→x)
foreveryxandyin [0,1].
(2)For a setX,thefuzzyequalityEXon FRel(X)isgivenby
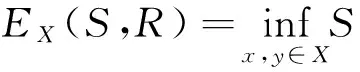
forallfuzzyrelationsSandR.
3 The degree of the symmetry of fuzzy relations
AfuzzyrelationRissymmetricifandonlyifthereissomesymmetricfuzzyrelationSsuchthatR=S.Replacethecrispequalitybythefuzzyequality,weobtainthefollowing:
Definition 1 Given a fuzzy relationRonasetX,thedegreeofthesymmetryofRisgivenby
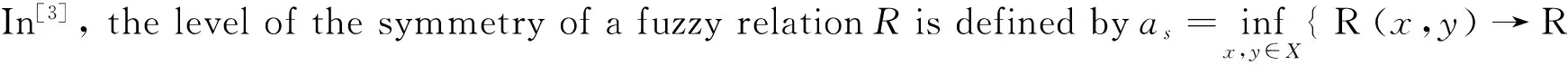
Proposition 1 A fuzzy relationRonasetXissymmetricifandonlyifD(R)=1.
Proof By Definition 1, ifRissymmetric,oneobtainsthatD(R)=1 clearly. Conversely, ifD(R)=1, butRis not symmetric, then there existx,yinX, such thatR(x,y)≠R(y,x). LetR(x,y) h(α)=(α↔R(x,y))∧(α↔R(y,x)), First,itholdsthath(α)≤R(y,x)→R(x,y)<1if0≤α≤R(x,y)orR(y,x)≤α≤1. Second,ifR(x,y)<α Letε0=(1-c)/4, then there exist δ0>0, for anytin (R(y,x)-δ0,R(y,x)), it holds that R(y,x)→t>t→R(x,y) Now,wetakesomet0in (R(y,x)-δ0,R(y,x)), thenh(α)≤R(y,x)→t0<1. Lemma 1 Let & be one of the t-norms in Example 1 The function h(x)=(x↔a)∧(x↔b) iscontinuousforalla,bin [0,1] witha Proof To proveh(x) is continuous, we need calculate (x↔a)∧(x↔b)foreachofthefourt-norms. So,ineachcase,wecanseethath(x) is continuous. Theorem 1 Let & be one of the t-norms in Example 1 andRbe a fuzzy relation on a setX, then there exists a symmetric fuzzy relationSsuch thatEX(S,R) is maximal. Proof IfR(x,y)=R(y,x), let S(x,y)=S(y,x)=R(x,y). IfR(x,y)≠R(y,x), by Lemma 1, the function h(α)=(α↔R(x,y))∧(α↔R(y,x)) iscontinuous.Thus,thereissomeelement,sayS(x,y), such thath(S(x,y)) is maximal. Clearly, the fuzzy relationSgiven in this way is a symmetric fuzzy relation as desired. Theorem 2 Let & be one of the t-norms in Example 1 andRbe a fuzzy relation on a setX, then there is some symmetric fuzzy relation S onXsuch thatD(R)=EX(S,R). [1] Klement E P, Mesiar R, Pap E. Triangular Norms[M]. Kluwer Academic Publisher, Dordrecht, 2000. [2] Alsina C, Frank M J, Schweizer B. Associative Functions: Triangular Norms and Copulas[M]. World Scientific Press, Singapore, 2006. [3] D Boixader, J Recasens. Approximate Fuzzy Preorders and Equivalences Proc[C]. ∥Fuzzy IEEE 2009. Korea,2 000. [4] D Boixader, J Recasens. Approximate Fuzzy Preorders and Equivalences: A similarity based approach[C]. Proc Fuzzy IEEE 2010, Spain,2 000. 2016-08-20 国家自然科学基金项目(11tp1297)资助 但业星,E-mail:danyexing09@163.com. 模糊关系的对称度 但业星 (四川大学数学学院,四川成都610064) 本文基于集合X上的模糊关系的模糊相等关系,讨论了模糊关系的对称度问题. 模糊关系,对称度,对称的模糊关系,模糊相等 O175.2 A 1672-6634(2017)01-0001-04 O175.2 Document Dode A Article ID 1672-6634(2017)01-0001-04