考虑位移约束的功能梯度结构ICM拓扑优化方法
杨旭静+胥海波+郑娟


摘 要:基于独立连续映射方法(Independent Continuous and Mapping,ICM),实现功能梯度材料(Functionally Graded Material,FGM)结构的拓扑优化设计.通过引入过滤函数,构建FGM-ICM材料模型.结合梯度位移函数,建立以结构质量最小化为目标、以位移为约束条件的功能梯度材料结构拓扑优化近似显式模型.采用线性衰减的过滤方法避免棋盘格现象和网格依赖性问题.另外,为得到边界清晰的拓扑构型,设计拓扑变量阈值动态调整策略(Dynamic Adjustment Strategy for Variable Threshold,DASVT),消除了拓扑变量阈值取值的盲目性.通过数值算例验证了该方法的可行性和有效性,最终实现了功能梯度材料结构ICM拓扑优化设计.
关键词:结构拓扑优化;功能梯度材料;ICM方法;位移约束;变量阈值动态调整策略
中图分类号:O342 文献标志码:A
ICM Topology Optimization Method of Functionally Graded Structures Considering Displacement Constraint
YANG Xujing, XU Haibo, ZHENG Juan
(State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082, China)
Abstract:Topology optimization of functionally graded material structure was presented based on independent continuous and mapping method. By introducing the filter function, the FGM-ICM model was constructed. Combined with the gradient displacement function, the approximate explicit model for ICM structural topology optimization of FGM was established. The filter method of linear attenuation was adopted to avoid the checkerboards and mesh dependency problem. Meanwhile, in order to obtain the clear topological configuration, the dynamic adjustment strategy for the topological variable threshold was proposed. The results of numerical examples demonstrate that the proposed analysis method can effectively realize the structural topological optimization of FGM.
Key words:topology optimization; functionally graded materials; ICM method; displacement constraint; dynamic adjustment strategy for variable threshold
功能梯度材料是根據其服役环境的使用要求,选择两种或两种以上不同性能的材料,在制备过程中通过控制各组分量在空间位置上的连续变化而制成的一种新型材料[1].国内外学者分别采用了理论计算和数值模拟仿真分析研究了功能梯度材料结构优化策略.龙述尧等[2]提出一种新的无网格局部径向点插值法来分析功能梯度材料.Fadel[3]采用已应用的熔融沉积成型技术(Fused Deposition Modeling,FDM)解决了在打印功能梯度材料对象过程中的成型困难问题.杨东生等[4]研究了FGM微观非均质性对整体热力学性能的影响,并发展了FGM热应力分析的耦合扩展多尺度有限元方法.黄桂芳等[5]在研究一维非线性功能梯度材料的不对称热传导性质过程中采用了非平衡分子动力学方法,并引入线性质量梯度.
结构拓扑优化设计在近几十年得到了迅速发展,其方法主要有均匀化方法[6]、渐进结构优化方法[7]、变密度法[8]和独立连续映射方法(Independent Continuous and Mapping,ICM)[9]等.拓扑优化设计是在给定的设计域内通过增删材料获得最佳的构型,由设计变量函数控制材料的分布,采用有限元离散方法数值求解,将设计域划分成单元网格形式,设计变量函数也相应地被离散成一个个单元变量函数.张伟等[10]提出了一种结合拓扑优化和车身尺寸优化的优化设计方法,建立了从整车拓扑结构到车身梁截面的优化设计模型,实现了电动汽车白车身的轻量化设计.因此,连续体结构拓扑优化的设计方法与功能梯度材料的材料性能有着相似之处,本质上都是考虑了材料属性的连续性变化.Xia等[11]基于水平集方法,以体分比和结构边界为设计变量实现了功能梯度结构的材料性能和拓扑布局的并行优化设计.邱克鹏等[12]基于SIMP模型,采用凸规划求解策略以及周长控制方法,实现了功能梯度MBB梁和功能梯度夹层结构中央芯的拓扑构型设计,揭示了材料性能和材料模型对结构优化中材料分布的影响规律.Radman A等[13]将FGM假定成各个自由方向上是由许多基细胞组成,通过双向渐进结构法(Bi-directional evolutionary structural optimization,BESO)一次性优化3个相邻基细胞,提高了计算效率,实现了FGM的BESO拓扑优化设计.
本文引入识别杨氏模量的过滤函数,建立FGM-ICM (Functionally Graded Material-Independent Continuous Mapping) 材料模型,基于ICM方法,以功能梯度材料结构质量最小为目标,在满足位移约束的前提下,采用约束限自适应调整策略,设计了MBB梁和悬臂梁的功能梯度结构的拓扑构型,分析了在求解过程中结构质量、结构位移和单元离散度的变化规律.在材料性质和功能呈梯度变化的同时,实现了功能梯度结构的轻量化设计.
1 优化模型的建立
1.1 FGM-ICM材料模型
ICM法以独立于单元具体物理参数的变量来表征单元的有无.对于FGM结构,杨氏模量在设计域内并不是一个常数,是按照指定关系以一定的规律变化的.根据FGM的特性,本文引入过滤函数fe(t)识别材料的杨氏模量,建立FGM-ICM材料模型,如式(1)所示.
式中:EH是FGM杨氏模量,随着设计域内坐标值的变化而变化;E0是基体杨氏模量;a和b是定义材料性能的变化参数;x和y是结构内各点的坐标值.
常见的过滤函数形式有幂函数、复合指数函数等,本文采用幂函数形式的过滤函数,即
其中β是杨氏模量过滤函数幂指数.
采用有限元方法对FGM结构设计域进行离散后,单元杨氏模量为该单元中每个节点处杨氏模量的平均值,即
式中:EHi是单元i的杨氏模量;ti是单元i的拓扑设计变量;m是单元i中节点个数;xji和yji分别是单元i中第j个节点的坐标值.
1.2 优化模型
为了实现拓扑变量由连续性向“0-1”离散型的靠拢,本文引入单元拓扑变量过滤函数fm(ti)
式中:mi表示单元质量;m0i为单元固有质量;α为结构质量过滤函数幂指数.
以结构质量最小化为优化目标,更加符合工程实际应用,故本文采用的是在满足性能指标下结构经济指标最小化问题的代表模型——基于ICM方法的位移约束下结构质量最小化模型,如式(6)所示.
式中:t=(t1, … ,tN)T为单元拓扑设计变量向量;u(t)為结构位移函数,即某载荷下,从根本上影响结构拓扑最优构型的节点的位移函数;为单元节点的位移上限值;N为设计域内单元总数.为了避免在优化迭代过程中出现奇异矩阵,取tmin =0.001.
2 优化模型的建立
2.1 节点梯度位移函数的显式化
由Mohr定理可知,结构上某节点的位移可通过虚功计算表示,即
式中:wi=σTRεvdv为单元i对节点位移贡献的积分形式;σR和εv分别为单元i在实载荷下的应力分量和虚载荷下的应变分量.
另外,外力在虚位移上做的功等于内力在虚位移导致的虚变形上所做的虚功,因此根据有限元分析方程可得
式中:FRi与uvi分别为单元i在实载荷下的单元力向量和虚载荷下的单元位移向量;Ki与Fvi分别为单元i的单元刚度阵和虚载荷下的单元力向量.
因为单元刚度矩阵与单元杨氏模量成正比,可得FGM设计域中单元刚度矩阵为:
式中: K0i是单元杨氏模量为E0i时的单元刚度矩阵.
将式(9)和式(8)代入式(7),可得梯度位移函数,即
式中:D0i≈FRiTK0i-1Fvi为单元i对节点位移的贡献分量系数.
2.2 优化模型的求解
为了分析拓扑变量对节点位移的贡献,由式(10)对拓扑变量求偏导数得
当-D0i>0时,uti>0,单元拓扑变量ti和位移u成正相关,即增大单元的拓扑变量值,结构位移值相应变大.称该拓扑变量为消极变量.
当-D0i≤0时,uti<0,单元拓扑变量ti和位移u成负相关,即增大单元的拓扑变量值,结构位移值相应减小.称该拓扑变量为积极变量.
积极变量集合记为Ia={i|D0i≥0,i=1,…,m}.
在优化求解的每次迭代中,可知消极变量集中的拓扑变量值保持不变,将式(10)代入优化模型式(6)中得到近似显示优化模型
2.3 约束限自适应动态调整策略
在推导求解优化模型(12)的过程中,为了解决约束函数值达不到约束上限或者约束超限问题,本文在优化模型的求解过程中引入约束限自适应动态调整方法[15],即
2.4 变量阈值动态调整策略
为了得到边界清晰的结构,本文采用拓扑变量阈值动态调整策略(Dynamic Adjustment Strategy for Variable Threshold,DASVT)定义拓扑变量阈值t,如式(18)所示,即拓扑变量阈值t随着迭代次数变化做动态调整.
2.5 收敛准则及优化流程
拓扑优化的优化收敛准则是基于拓扑构型的变化程度确定的,因此,本文以离散度的变化率作为收敛准则,即
3 优化模型的建立
3.1 MBB梁的功能梯度结构设计
如图2所示, MBB梁的高H=1 m,长度L=6 m,相对结构质量为5.实体杨氏模量为E0=2×108 Pa,泊松比为υ=0.29,上端中间作用一向下集中载荷F=1 000 N,设定结构位移的约束上限值=20.3 mm.
将设计域离散为10×60=600个四边形单元,收敛精度ε = 0.001,为了突出FGM的材料性能呈现梯度变化,以及比较FGM结构设计域内材料性能改变对优化结构的影响,对材料模型式(3)中参数a和b分别取不同的值:①a=0,b=0;②a=0.06,b=0;③a=0,b=0.06;④a=0.06,b=0.06.
1)a=0,b=0
在这种情况下,MBB梁为均质材料,设计域内各处的材料性能一样,所以得到的是关于左右对称最优构型,如图3所示.
2)a=0.06,b=0
在这种情况下,MBB梁的杨氏模量沿x方向逐渐增大,沿y方向保持不变,所以其最优构型是非对称的,沿x方向呈现梯度变化,所用材料逐渐减少,如图4所示.
3)a=0,b=0.06
在这种情况下,MBB梁的杨氏模量沿y方向逐渐减小,沿x方向保持不变,所以其最优构型是左右对称的,沿y方向呈现梯度变化,所用材料增加,如图5所示.
4)a=0.06,b=0.06
在这种情况下,MBB梁的杨氏模量沿x方向逐渐增大,沿y方向逐渐减小,所以其最优构型是非对称的,沿x方向和y方向呈现梯度变化,沿x方向所用材料减少,沿y方向所用材料增加,如图6所示.
通过以上4种情况的计算结果对比,所得到的优化构型与FGM的材料性能相一致,结果表明,基于ICM方法的FGM拓扑优化设计方法具有可行性和有效性.
3.2 悬臂梁功能梯度结构设计
如图7所示,悬臂梁的高H=2 m,长度L=6 m,相对结构质量为10.实体杨氏模量为E0=2×108 Pa,泊松比为υ=0.29.右下端作用一向下集中載荷F=500 N,设定结构位移的约束上限值=20.2 mm.
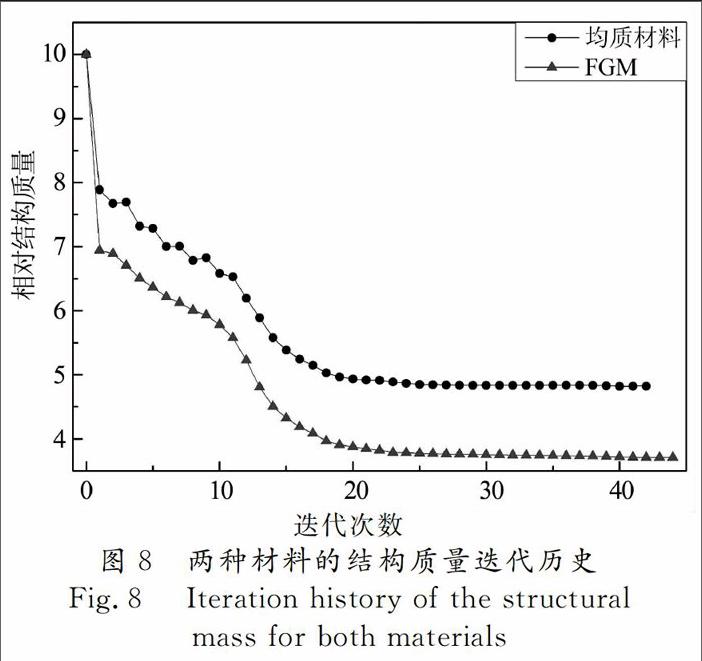
同样将设计域划分成20×60=1 200个四边形单元,收敛精度ε = 0.001,为了对比本文拓扑优化设计方法在对均质材料(a=0,b=0)和功能梯度材料(a=0.02,b=0.01)拓扑构型优化过程中的不同,分别绘制了两种材料在迭代过程中结构质量、结构位移以及离散度的变化曲线(如图8~图10),随着迭代次数的增加,各项参数趋于稳定,并得出两种材料的优化构型图(如图11).
如表1所示,采用本文提出的结构拓扑优化算法,以结构质量最小为优化目标,均质材料结构迭代次数为42次,优化后相对结构质量为4.823,单元离散度为15.74%,FGM结构迭代次数为44次,优化后相对结构质量为3.710,单元离散度为15.62%.结果表明,在约束条件和边界条件相同的情况下,所得到的最优结构,功能梯度材料结构质量比均质材料结构质量减轻了22.9%,功能梯度材料单元离散度较好.
3.3 带孔悬臂梁FGM结构拓扑优化设计
如图12所示,带孔短悬臂梁的高H=4 m,长度L=6 m,圆孔的中心坐标为(20, 20),半径为r=2 m,相对结构质量为10.实体杨氏模量为E0=2×108 Pa,泊松比为υ=0.29.右下端作用一向下集中载荷F=500 N.设定结构位移的约束上限值=3.59 mm.
为了对比变量阈值动态调整策略(DASVT)对FGM结构拓扑构型的影响,分别计算了采用DASVT和未采用DASVT两种情况的结果(如表2),获得最优构型(如图13).结果表明,采用DASVT的单元离散度为0,得到的优化结果具有清晰的边界.
4 结 论
本文基于ICM方法,实现了功能梯度材料结构的拓扑优化设计.
1)通过引入识别单元杨氏模量过滤函数,建立了功能梯度材料结构的FGM-ICM材料模型.
2)基于ICM方法,结合节点梯度位移函数,以位移为约束条件,建立了功能梯度材料结构拓扑优化近似显式模型.引入自适应约束限调整策略,通过计算离散度来检验单元设计变量值的收敛情况,实现了功能梯度材料结构拓扑优化设计.
3)采用拓扑变量阈值动态调整策略(DASVT)定义拓扑变量阈值,消除了拓扑变量阈值取值的盲目性.
4)通过算例对比了均质材料结构和功能梯度材料结构的拓扑优化计算结果,验证了本文方法的可行性和有效性.通过本文方法,合理地利用功能梯度材料的特性,可有效减轻材料结构设计重量,实现结构轻量化设计.
参考文献
[1] KOIZUMI M. The concept of FGM[J]. Functionally Gradient Material,1993, 34: 3-10.
[2] 龙述尧,刘凯远,李光耀.功能梯度材料中的无网格局部径向点插值法[J].湖南大学学报:自然科学版,2007,34(3):41-44.
LONG Shuyao, LIU Kaiyuan, LI Guangyao. A meshless local radial point interpolation method for the analysis of functionally graded materials[J]. Journal of Hunan University: Natural Sciences, 2007,34(3):41-44.(In Chinese)
[3] FADEL G. Design and manufacturing functionally gradient material objects with an off the shelf three-dimensional printer[J]. Journal of Mechanical Design, 2015, 137: 11407.
[4] 杨东生,张盛,张洪武.基于耦合扩展多尺度有限元方法的功能梯度材料热应力分析[J].复合材料学报,2015,32(4):1107-1117.
YANG Dongsheng, ZHANG Sheng, ZHANG Hongwu. Thermal stress analysis of functionally graded material based on coupling extended multiscale finite element method[J]. Acta Materiae Compositae Sinica, 2015,32(4):1107-1117.(In Chinese)
[5] 黄桂芳,詹斯琦,黄维清.一维非线性功能梯度材料的热整流反转[J].湖南大学学报:自然科学版,2015,42(10):102-106.
HUANG Guifang, ZHAN Siqi, HUANG Weiqing. Thermal rectification reversal in one-dimensional nonlinear function graded materials[J]. Journal of Hunan University: Natural Sciences, 2015,42(10):102-106.(In Chinese)
[6] BENDSOE M P, KIKUCHI N. Generating optimal topologies in structural design using a homogenization method[J]. Computer Methods in Applied Mechanics and Engineering, 1988, 71(2): 197-224.
[7] XIE Y M, STEVEN G P. A simple evolutionary procedure for structure optimization[J]. Computers and Structures, 1994, 11(5): 295-302.
[8] MLEJNEK H P, SCHIRRMACHER R. An engineers approach to optimal material distribution and shape finding[J]. Computer Methods in Applied Mechanics and Engineering, 1993, 106(1/2): 1-26.
[9] SUI Y K, YANG D Q. A new method for structural topological optimization based on the concept of independent continuous variables and smooth model[J]. ACTA Mechanica Sinica, 1998, 18(2): 179-185.
[10]張伟,侯文彬,胡平.基于拓扑优化的电动汽车白车身优化设计[J].湖南大学学报:自然科学版,2014,41(10):42-48.
ZHANG Wei, HOU Wenbin, HU Pin. The body in white optimization of an electric vehicle using topology optimization[J]. Journal of Hunan University: Natural Sciences, 2014,41(10):42-48.(In Chinese)
[11]XIA Q, WANG M Y. Simultaneous optimization of the material properties and the topology of functionally graded structures[J]. Computer Aided Design, 2008, 40: 660-675.
[12]邱克鹏,张卫红.功能梯度材料结构拓扑优化设计研究[J].西北工业大学学报,2010,28(6):851-857.
QIU Kepeng, ZHANG Weihong. Improving topological design of FGM (Functionally Graded Material) structure[J]. Journal of Northwestern Polytechnical University, 2010,28(6):851-857.(In Chinese)
[13]RADMAN A, HUANG X, XIE Y M. Topology optimization of functionally graded cellular materials[J]. Journal of Materials Science, 2013, 48(4):1503-1510.
[14]SUI Y K, PENG X R. The ICM method with objective function transformed by variable discrete condition for continuum structure[J]. Acta Mechanica Sinica, 2006, 22(1): 68-75.
[15]易桂莲,隋允康.解决约束违背问题的一种自适应调整方法[J].计算力学学报,2014,31(3):303-309.
YI Guilian, SUI Yunkang. An adaptive adjustment approach for solving breach issues of constraints[J]. Chinese Journal of Computational Mechanics,2014,31(3):303-309.(In Chinese)
[16]SIGMUND O. Morphology-based black and white filters for topology optimization[J]. Structural Multidisciplinary Optimization, 2007, 33(4/5): 401-421.

