Control allocation for aircraft with input constraints based on improved cuckoo search algorithm

Yo LU,Cho-yng DONG,Qing WANG

aSchool of Aeronautic Science and Engineering,BUAA,Beijing 100191,China

bSchool of Automation Science and Electrical Engineering,BUAA,Beijing 100191,China

Control allocation for aircraft with input constraints based on improved cuckoo search algorithm

Yao LUa,*,Chao-yang DONGa,Qing WANGb

aSchool of Aeronautic Science and Engineering,BUAA,Beijing 100191,China

bSchool of Automation Science and Electrical Engineering,BUAA,Beijing 100191,China

A R T I C L E I N F O

Article history:

Received 21 August 2016

Received in revised form

9 November 2016

Accepted 10 November 2016

Available online 23 December 2016

Control allocation

Optimization

Cuckoo search algorithm

Innovative control effector aircraft

Tracking

The control allocation problem of aircraft whose control inputs contain integer constraints is investigated.The control allocation problem is described as an integer programming problem and solved by the cuckoo search algorithm.In order to enhance the search capability of the cuckoo search algorithm,the adaptive detection probability andamplification factor are designed.Finally,the control allocation method based on the proposed improved cuckoo search algorithm is applied to the tracking control problem of the innovative control effector aircraft.The comparative simulation results demonstrate the superiority and effectiveness of the proposed improved cuckoo search algorithm in control allocation of aircraft.

©2016 The Authors.Published by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1.Introduction

As the development of the aircraft technology,for superior maneuver and reliability,more and more advanced aircraft,even unmanned aerial vehicles and missiles,deploy multiple and redundant effectors on their bodies.Therefore,an appropriate control allocation method is necessary for the control systems of these aircraft to use their effectors ef ficiently.Control allocation is a hot issue in the field of flight control.Many methods have been proposed for solving various control allocation problems[1].Most of the time,the control allocation problem can be represented as an optimization problem.Therefore,the designed control allocation methods are usually based on some optimization methods.

For an aircraft,its control allocation problem is apparently related to its effectors.Sometimes some unconventional effectors will make the control allocation problem different from the conventional problems and dif ficult to be solved.A characteristic example is the innovative control effector(ICE)aircraft which is introduced by Lockheed Martin Tactical Aircraft Systems[2].This aircraft uses several distributed arrays each of which contains lots of actuators as effectors.The particularity is that each actuator can only provide either full or no control energy[3].We can group those actuators which have almost the same full control energies together and then the control allocation problem of the ICE aircraft can be translated into an integer programming problem with some constraints.Actually,the integer constraints are present in many aircraft effectors,such as the reaction control system(RCS)and so on.

Different from the normal linear programming or quadratic programming problem,most of the integer programming problems are non-deterministic polynomial hard(NP-hard)problems and their optimum solutions are usually hard to be obtained.Some classical methods,such as the branch-bound method and cutting plane method,are usually used to solve the integer linear programming problem and they are effective when the scale of the problem is small.However,with the increase of the scale of the problem,the computational complexities of the classical methods will increase rapidly and cannot meet the practical requirements. Therefore,the metaheuristic algorithms have attracted more and more attentions.There have been recently many studies using metaheuristic algorithms to solve aircraft control allocation problems[4-7].The cuckoo search algorithm(CSA)is a relatively novel and promising metaheuristic algorithm proposed by Yang and Deb [8].Some studies have demonstrated that its search capability is better than many other metaheuristic algorithms[9,10].Therefore, the CSA has been applied to many application domains,such asparallel machine scheduling[11],total cost of ownership for supplier selection problem[12],maximum power point tracking for Photovoltaic System[13]and structural damage identi fication[14]. However,the ef ficiency of the basic CSA is still unsatisfactory. Therefore,the algorithm need be improved when it is used.

In this paper,an improved CSA is proposed for solving the aircraft control allocation problem with integer constraints.The remaining sections of this paper are organized as follows.Section 2 describes the aircraft control allocation problem with integer constraints.Section 3 formulates the design of the control allocation method based on an improved CSA.The simulation results established upon the proposed method and some compared methods are given in Section 4.Finally,some concluding remarks are summarized in Section 5.

2.Problem formulation

2.1.Description of the aircraft model

Consider the linearized dynamic model of aircraft

where x∈Rc1represents the states and v∈Rc2represents the virtual control input.The control objective is to track a reference model

where r（t）is the reference input.Assume that the system（A，Bv）is known and controllable,then the virtual control law can be designed as

where K1，K2are the gain matrices which meet the following matched conditions

Let e represent the tracking error.Under the virtual control law (3)the tracking error dynamical system can be described by

The system(5)shows that the tracking error e is asymptotically stable provided Amis a Hurwitz matrix.

2.2.Control allocation problem

After obtaining the virtual control input v,the control system on the aircraft need deploy the effectors to achieve it.Let n=［n1，…，nc3］Trepresent the actual control command from the effectors.Assume that ni，i=1，2，…，c3is restricted to the following compact setΩi

and the effector model is a linear model in the form

The objective of control allocation is to find out a suitable actual control command n to achieve the virtual control input v.Then the problem can be converted into an integer programming problem and the fitness function is defined as

where C is a de finite weighting matrix,‖·‖2is 2-norm.

It should be noticed that we cannot obtain the actual control command by rounding n=B+uv where（·）+represents pseudoinverse because the solution is inexact.Next,we propose an improved CSA for the design of the control allocation method.

3.Design of control allocation method

3.1.Basic cuckoo search algorithm

The CSA combines the cuckoo breeding behavior with a random walk called L′evy flight.Some studies have demonstrated that L′evyflight is an optimized search pattern for non-replenishable targets at unknown positions[15,16].The CSA is established based on the following three idealized rules[8]:

1)Each cuckoo lays only one egg once and places it in a random nest.

2)The best nest including the high quality egg will be carried over to the next generation.

3)The egg can be discovered by the nest owner with a detection probability pa∈［0，1］.When one egg is discovered,the nest owner will abandon the nest and build a new one in somewhere.

Controlled by the detection probability paand a random number θdrawn from a uniform distributionθ～U（0，1）,the CSA uses a combination of local random walk and global explorative random walk to search the optimum solution.Letτgjrepresent the j-th cuckoo in the population of g-th generation.When generating a new solutionτg+1j,if pa!θ,the global random walk is performed via L′evy flights

whereα＞0 is theamplification factor,⊗denotes Hadamard multiplication,L（λ）=［l1（λ），…，lc3（λ）］Tis the random step path and li（λ）follows the L′evy distribution

whereλis a L′evy flight parameter,li（λ）can be obtained by

whereβ=λ-1,μandνare drawn from normal distributions

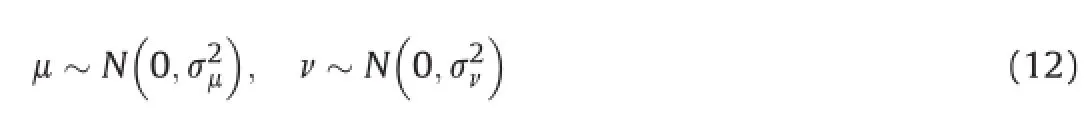
whereσμ，σνrepresent the standard deviations of the corresponding normal distributions and the values are

whereΓis the standard Gamma function.

Fig.1.The configuration of ICE aircraft.

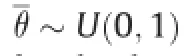
3.2.Improved cuckoo search algorithm

Similar to the other metaheuristic algorithms,the process of the CSA is of randomicity.It can be observed from the generative mechanism of the solutions of CSA that the characteristic of updated population is controlled by two parameters,detection probability andamplification factor.However,the two parameters are aptotic in basic CSA;this form is open-loop and cannot re flect the dynamic of the search process.Therefore,it is necessary for CSA to introduce some dynamic adjustment mechanisms to make the parameters of the algorithm adaptable to the speci fic situation of the search process.The speci fic improvements are designed as follows.

1)Detection probability

Generally,during the initial phase of the search process,the global search is preferred for extensive exploration and during the final phase the local search is preferred for rapid convergence.On the other hand,it is proved that larger detection probability is good for global search and smaller detection probability is good for local search.Thus,according to the Rechenberg's 1/5 criteria which considered that the successful proportion of all the mutation actions should be 1/5[17],the following adaptive method is adopted towards the detection probability

where g is the present iterative number,gmaxis the maximum number of iterations.Under the designed dynamic detection probability,the mutation rate in the whole searching process is about 0.2 on average.

2)Ampli fication factor

Theamplification factor can adjust the length of the random step path produced via L′evy flights.Due to the differences among the nests,the amplification factor of each nest should be adaptively adjusted according to its quality.The low-quality nest should be assigned a largeamplification factor for searching high-quality areas and the high-quality nest should be assigned a small amplification factor for searching the optimum solution around its location.Thus,the following adaptive method is adopted towards the ampli fication factor

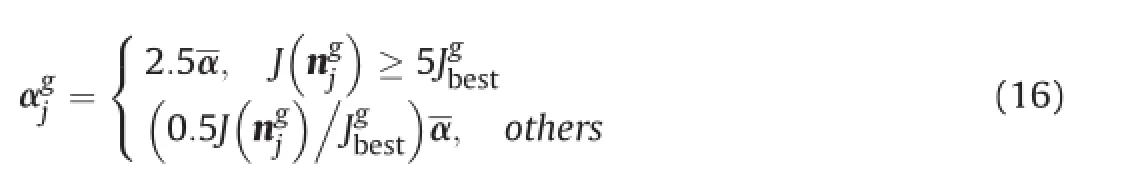
3.3.Bounds of the nests

4.Simulation

In this section,the effectiveness of the proposed improved CSA in aircraft control allocation is verified.The control allocation method based on the proposed algorithm is applied to the ICE aircraft linearized lateral-directional model which can be described via Eq.(1).The states x∈Rc4can be defined as x=［V p r φ］Twhere V represents the body-axis lateral velocity,p，r and φ represent the body-axis roll rate,yaw rate and roll angle,respectively.The configuration is illustrated in Fig.1.

The parameters of the ICE aircraft model are given as follows [6,7]

Table 1The bounds of the nests.

Table 2The parameters of the improved CSA.

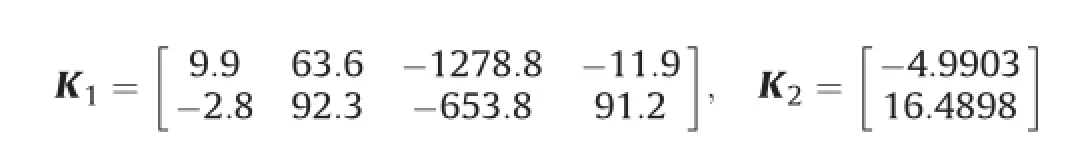
The reference model and reference input are[6,7].

Table 3The statistical results based on two algorithms.

Fig.2.The optimization convergence processes based on two algorithms.

The matrix Buand de finite weighting matrix C are

The bounds of nests are given in Table 1.

The parameters of the improved CSA are shown in Table 2.

First,the performance of the proposed improved CSA is studied. The individual optimization problem(8)is solved by the proposed algorithm.For comparison,the basic CSA is introduced to solve the same problem.To eliminate the difference of each experiment,the improved CSA and basic CSA use the same initial population and random walks produced by L′evy flights and they are executed 50 times.The virtual control input is selected to be v=［7，-6］T.The comparative results are shown in Table 3.

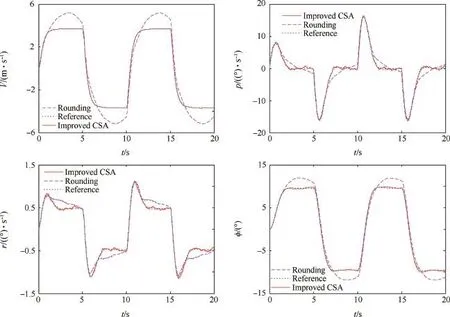
Fig.3.The state responses of the closed-loop system.

It can be seen that both of the mean and best fitness valuesunder the proposed improved CSA are better than the basic CSA. Fig.2 shows the typical search processes under the two algorithms. It can be observed that the search capability of the proposed improved CSA is better than the basic CSA.According to the comparative results it can be concluded that the proposed improved CSA is superior to the basic CSA.

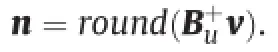
It can be observed that the tracking errors of the system states under the direct rounding method are obvious and the control allocation method based on the proposed improved CSA achieves better tracking performance.It can be concluded that the proposed control allocation method is necessary and effective for the tracking control of the ICE aircraft.

5.Conclusions

In this paper,an improved cuckoo search algorithm is proposed for solving the aircraft control allocation problem with integer constraints.Different from the basic cuckoo search algorithm with fixed parameters,the improved algorithm uses adaptive parameters varying according to the search progress and quality of each nest to enhance the algorithm search capability.The flight control system uses the improved algorithm to obtain the actual control commands.The ICE aircraft model is introduced for verifying the effectiveness of the proposed method.The comparative simulation results show that the proposed improved cuckoo search algorithm is superior to the basic algorithm and the tracking performance of the aircraft control system under the control allocation method based on the proposed algorithm is quite better than the contrastive method.

Acknowledgements

This work is supported by the National Natural Science Foundation of China(61273083 and 61374012).

[1]Johansen TA,Fossen TI.Control allocation-a survey.Automatica 2013;49(5): 1087-103.

[2]Raney DL,Montgomery RC,Green LL,Park MA.Flight control using distributed shape-change effector arrays.41st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics,and Materials Conference&Exhibit,AIAA Paper 2000-1560.April 2000.

[3]Ataei-Esfahani A,Wang Q.Robust failure compensation for a morphing aircraft model using a probabilistic approach.IEEE Trans Control Syst Technol 2007;15(2):324-31.

[4]Shao XY,Ren Z,Wang RL.New control allocation algorithm for three dimension problem based on genetic algorithm.In:33rd Chinese control conference(CCC).Nanjing,China:IEEE;July 2014.p.3766-70.

[5]Zhang HY,Chen M.Control allocation based on hybrid optimization fish swarm algorithm for near space vehicles.J Jilin Univ(Information Science Edition)2014;32(4):369-76[in Chinese].

[6]Jiang WL,Dong CY,Wang T,Wang Q.Fault tolerant control based on control allocation for morphing aircraft model.J Beijing Univ Aeronaut Astronaut 2014;40(3):355-9[in Chinese].

[7]Dong CY,Lu Y,Jiang WL,Wang Q.Fault tolerant control based on cuckoo search algorithm for a class of morphing aircraft.Acta Aeronautica et Astronautica Sinica 2015;36(6):2047-54[in Chinese].

[8]Yang XS,Deb S.Cuckoo search via L′evy flights.In:Proceedings of the world congress on nature&biologically inspired computing(NaBIC’09).Coimbatore,India:IEEE;2009.p.210-4.

[9]Yang XS,Deb S.Cuckoo search:recent advances and applications.Neural Comput Appl 2014;24(1):169-74.

[10]Civicioglu P,Besdok E.A conceptual comparison of the cuckoo-search,particle swarm optimization,differential evolution and arti ficial bee colony algorithms.Artif Intell Rev 2013;39(4):315-46.

[11]Guo P,Cheng WM,Wang Y.Parallel machine scheduling with step deteriorating jobs and setup times by a hybrid discrete cuckoo search algorithm.Eng Optim 2015;47(11):1564-85.

[12]Kanagaraj G,Ponnambalam SG,Jawahar N.Reliability-based total cost of ownership approach for supplier selection using cuckoo-inspired hybrid algorithm.Int J Adv Manuf Technol 2016;84:801-16.

[13]Shi JY,Xue F,Qin ZJ,Zhang W,Ling LT,Yang T.Improved global maximum power point tracking for photovoltaic system via cuckoo search under partial shaded conditions.J Power Electron 2016;16(1):287-96.

[14]Xu HJ,Liu JK,Lv ZR.Structural damage identi fication based on modi fied cuckoo search algorithm.Struct Eng Mech 2016;58(1):163-79.

[15]Shlesinger MF.Mathematical physics:search research.Nature 2006;443(7109):281-2.

[16]Reynolds AM,Smith AD,Menzel R,Greggers U,Reynolds DR,Riley JR.Displaced honey bees perform optimal scale-free search flights.Ecology 2007;88(8):1955-61.

[17]Back T.Evolutionary algorithms in theory and practice.Oxford,UK:Oxford University Press;1996.

[18]Tao G,Chen SH,Fei JT,Joshi SM.An adaptive actuator failure compensation scheme for controlling a morphing aircraft model.In:Proceedings of the 42nd IEEE conference on decision and control.Maui,HI:United states;2003. p.4926-31.

*Corresponding author.

E-mail address:luyaosacred@126.com(Y.LU).

Peer review under responsibility of China Ordnance Society.