三角形重心和垂心的向量表示的充要条件及其运用

江苏省常州市北郊高级中学(213000) 姜小亚●



三角形重心和垂心的向量表示的充要条件及其运用

江苏省常州市北郊高级中学(213000)
姜小亚●

一、重心

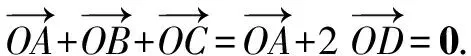
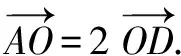
∴A、O、D三点共线，且O分AD为2∶1∴O是△ABC的重心.

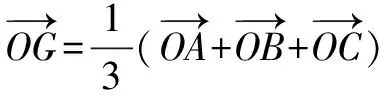
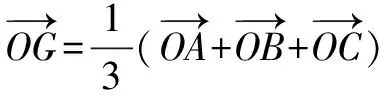
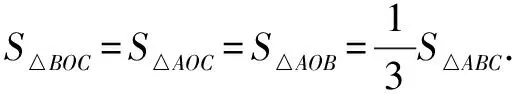
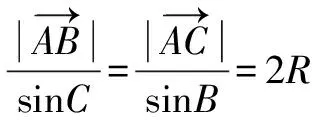
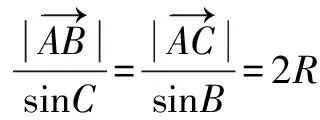
二、垂心

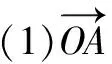
证明 若O是三角形ABC的垂心，BE垂直AC，AD垂直BC，D、E是垂足.

(2)O为斜△ABC的垂心(O在△ABC内部)，则S△BOC∶S△AOC∶S△AOB=tanA∶tanB∶tanC.

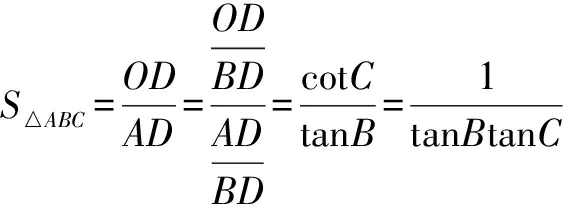
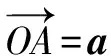
G632

B

1008-0333(2017)10-0045-01