基于关键词权重的XML查询结果排序方法①

魏东平, 苑志朋(中国石油大学(华东) 计算机与通信工程学院, 青岛 266580)

基于关键词权重的XML查询结果排序方法①

魏东平, 苑志朋
(中国石油大学(华东) 计算机与通信工程学院, 青岛 266580)

XML关键字查询结果质量不高的一个很重要的原因是查询关键词难以反映用户真实的查询意图, 而给关键词设置权重在一定程度上可以解决这一难题. 本文结合关键字之间的结构关系提出了一种新的结果排序方法, 该方法给查询关键词设置权重, 并参照查询关键词的权重给包含关键字的结点设定结点权重, 然后根据关系树中的结点权重和关键词之间结构关系[1]统计SLCA结点的重要程度, 再以此依据对查询结果进行排序, 最后返回给用户有序的查询结果. 实验结果和分析表明, 提出的排序方法具有较高的准确率, 能够较好地满足用户查询的需求和偏好.

XML; 关键字查询; 关键词权重; 结果排序

在信息检索领域, 关键词搜索是一种简单而高效的信息获取方式. 与XML结构化查询相比, XML关键字查询为用户提供了非常简单实用的查询接口, 操作比较简单、灵活, 对用户而言是一种比较友好且便捷的查询方式. 此外, 选择关键字查询不需要额外学习复杂的查询语言和书写准确的查询表达式, 更不需要深入了解XML复杂的文档结构, 用户只需要提供查询内容的关键字就可以检索需要的信息.

但是, 由于XML数据具有复杂的结构信息, 简单的关键字查询方法在准确表达查询意图方面差强人意.一种比较有效的方法是对查询结果进行排序. 对XML关键字查询结果的排序方法的研究已经取得了许多成果. XRank[2]将信息检索中的PageRank方法扩展到XML排序, 使XML文档的结构特征反映在排序中.在XSEarch[3]中使用了一种基于tf*idf的排序机制对查询结果进行排序. EASE[4]将基于tf*idf的信息检索排序机制与基于结构紧凑度的数据库排序机制相结合,实现在异构数据上的关键词搜索. XReal[5]设计了一个基于tf*idf的排序机制. 文献[6]则提出了一种XML关键词查询结果类型的推导方法, 但是没有对查询结果进行排序. 文献[7]则提出了一种可以有效排列组合成用户容易理解的查询结果.

1 问题的提出

考虑图1所示的XML文档实例, 关键字查询Q1为“xml, keyword, twig”, 用户的查询意图是要搜索有关XML、Keyword和twig的文献资料. 查询结果得到两个SLCA(最近最小公共祖先) 即SLCA1: Artile1和SLCA2: Artile3. 将查询Q1修改为查询Q2“xml, twig, keyword”后 Artile1 和Artile3 仍然是查询后的结果.对于当前的查询和排序方法而言, 查询Q1和Q2没有太大的区别, 因为它们由相同的关键字组成. 但是查询Q1和Q2的查询意图是有区别的, 查询Q1强调的是keyword查询而查询Q2更强调twig查询. 对于查询Q1, Artile1更符合用户的查询意图, 是一篇有关于XML keyword查询的文献. 而对于查询Q2, Artile3明显更符合用户的查询意图, 是一篇与XML twig查询相关的文献, 仅仅是涉及到了keyword查询的知识.因此, 针对查询Q1和查询Q2, 查询结果可以相同但是最后返回用户的查询结果排序应该是有所差异的.

图1 XML文档实例

由此可见, 即使两个查询中包含的关键词是相同的, 只是关键词的顺序不同, 为反映查询意图的差异性, 查询结果虽然相同但排序结果也应该有所不同.因此, 在查询结果排序时应该考虑关键词的顺序因素.

对于XML 关键词查询, 不能简单地看作是几个关键词的集合, 而应该将其看作是几个关键词的序列,在这个序列中隐含了某些真实的查询意图[8]. 为关键词设置权重可以在一定程度上反应用户的真实查询意图, 进而优先返回用户需要的查询结果.

2 有关概念和术语

定义1. XML树模型[9]. 一个XML文档可以看成是带标签的有向树D(r, V, E), r表示树的根结点, V表示结点集合, E表示边的集合.

定义2. Dewey编码. 给定对应XML数据的标签有向树G=(V, E, R, A), G中任意结点的扩展Dewey编码由下列规则确定:

(1) 根结点r的Dewey编码为“0”.

(2) 在宽度优先遍历G的过程中, 如果结点v是结点u的第i个孩子结点, 那么结点v的Dewey编码为“D(u).i-1”. 其中, D(u)表示结点u的Dewey编码.

定义3. 关键字匹配集合[9]. 给定XML文档D和关键字k, 用KMS(k)表示文档D中所有匹配关键字k的结点集合, KMS(k)={v|vV, ∈k=tag(v)或k=val(v)}.

定义4. 最小最低公共祖先SLCA(smallest lowest common ancestor). 即它包含所有关键字的最紧致片段.如果文档树中结点V已经包含所有查询关键字, 那么V的祖先结点就不应该再作为SLCA返回. 给定查询Q(k1,k2,…,kn), 我们说结果R满足SLCA语义, SLCA结点必须满足以下两个条件:

(1) R至少包含全部查询关键字一次, 所谓包含即关键字ki出现在以R为根的子树下.

(2) R的任意后代结点都不可能同样包含k1, k2, …, kn全部关键字.

定义5. 权重关系树[1]. 在搜索所得到的结果SLCA中保留包含关键字结点, 删除所有不包含关键字的结点并为关键字结点设置权重, 从而形成仅包含所有关键字的树形结构.

定义6. SLCA的重要程度. 权重关系树中所有结点的重要程度之和作为整个关系树的重要程度, 即关系树对应的SLCA结点的重要程度.

3 基于关键词权重的排序方法

3.1 Stack算法

Stack[10]算法的具体描述如下:

(1) 获取每个关键字倒排表, 选取关键字倒排表中最小Dewey编码初始化栈.

(2) 从所有关键字倒排表中剩余的Dewey编码中选取最小Dewey编码进行进栈处理.

(3) 判断最长的公共前缀, 对不包含最长的公共前缀的条目进行出栈处理. 当且仅当Keywords[i] = true(i[0,∈k]), 并且不会被下面的条目改变状态时Stack中保存的元素即为目标SLCA结点, 所有目标SLCA 结点构成的集合即为SLCA结点集.

3.2 根据关键词的权重设置关系树的关键字结点权重

用户在进行关键字查询时输入的关键字在一定程度上会反映出用户的查询意图, 而关键词的先后顺序会体现出用户对每个关键词的重视程度. 本文主要是通过直接输入关键词的权重或关键词的先后顺序来确定关系树中包含关键字的结点的权重. 在关键字查询时用户可以自己来指定每个关键词的权重大小, 关键字查询时输入的查询形式为(k1w1, k2w2, ……, knwn),其中, k为查询关键词, w为对应关键词的权重. 这种由用户直接确定关键词权重的方式虽然不方便, 但是可以更好地体现出用户的真实查询意图.

当用户未指定每个关键词的权重时由查询系统为关键词设置权重的大小. 我们设定权重时既要考虑到关键词的顺序又要考虑到关键字在文档中出现的频率,我们根据关键词的先后顺序并结合关键字在文档中出现的频率设定每个关键词的权重大小, 查询的关键词的权重大小定义为:

其中, R(0＜R≤1)为关键词权重递减的比例系数, N为文档的总数量, fk为包含关键字k的文档的数量. 例如查询Q3(XML, DTD, Query), 用户没有指定每个关键词的权重, 那么系统就会默认的设定关键词的权重. 就体现关键词顺序因素的权重而言, 一般情况下第一个关键词权重默认为1, 从第二个关键词开始关键词的部分权重会逐步递减, 权重递减率设定为R. 查询Q3的关键词权重就可以设置为XML: 1*ln(N/(fxml+1)), DTD: R*ln(N/(fDTD+1)), Query: R2*ln(N/(fQuery+1)), 其中R的值可以由用户指定, 也可以由系统默认设定,目的就是为每一个关键词预设好权重, 方便之后的结果排序.

由Stack算法求得的结点SLCA为根的子树中不仅包含了所有的查询关键词而且反映了结果子树中所有关键词的结构关系, 遍历以结点SLCA为根的结果子树, 记录每一层的非关键字结点并删除每个SLCA中所有的非关键字结点, 对SLCA中的关键字结点进行权重设置, 按照输入关键词查询时的设定的权重值为结果子树中所有的关键字结点赋权重值, 可以得到结点为带权重值的关键字的树形结构, 该结果子树中可以通过父——子关系和祖先——后代关系的位置关系反映出所有关键字之间的结构关系, 如算法1所示.

算法1. RTW(Relationship Tree with Weight)算法输入: SLCA结点链表S, 关键词权重输出: 权重关系树, 数组a For each SLCAS Do∈Traversal(SLCA);//遍历以SLCA结点为根的子树if 结点为非关键字结点{a[i]←每层非关键字结点个数

4 根据结点重要程度对查询结果排序

4.1 关键字结点的重要程度

在查询所得的SLCA转化成为的关系树中, 所有关键字结点的权重值与关键字结点对查询结点的严格程度结合后可以反映出该关系树对查询结果的重要程度, 该关系树对查询结果的重要程度越高, 则该关系树对应的查询结果应该更加符合用户的查询意图, 应该优先返回给查询用户.

在权重关系树中, 不同位置的关键字结点对应的对查询结点Q的要求是不同的, 不同的关键字的结点对应的权重也是不相同的, 因此关系树中各关键字结点相对于查询结点的重要程度是不同的. 单就结构方面而言, 关系树中查询结点的子结点是最重要, 查询结点的后代结点中距离查询结点的层次越深, 结点相对于查询结点的重要程度就越低. 如图2所示, 结点的重要程度依次为a1＞a2, b1＞b2＞b3, c1＞c2＞c3.

图2 关系树

假设查询结点Q的重要程度默认为1, 则设定中间结点的重要程度小于1. 设father=a*childhood, ancestor=b*offspring, 其中a, b分别为父亲——孩子或祖先——后代重要程度的递减系数, 因此中间结点的重要程度为:

(1) 父亲——孩子关系: pn=a*pn-1. 其中, pn是pn-1的孩子. 如图2中: a1=a*1=a.

(2) 祖先——后代关系: pn=b*pn-1. 其中, pn是pn-1的后代. 如图2中: c2=b*(a*1)=b*a.

按上述方法, 假设输入的关键字为a2, b2, c3, 设定权重递减率为R, 则对应的关键字结点的重要程度为:

4.2 非关键字结点的重要程度

根据在生成关系树时返回的每一层非关键字结点的数量统计以SLCA结点为根的子树中所有非关键字结点的重要程度, 相比较关键字结点的重要程度, 非关键字结点的重要程度所占比重要相对较低. 我们设定根节点的权重值为1, 从根节点往下每一层的非关键字结点的权重值逐渐减小, 我们设定权重的递减率为k(0＜k≤1), 则每个SLCA中的所有非关键字结点的权重值为:

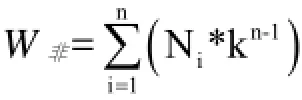
其中Ni为每一层的非关键字结点的数量, k也可以看做是每一层的非关键字结点的权重大小.

每个SLCA的重要程度可以表示为关键字结点和非关键字结点的和, 为突出关键字结点的重要程度的重要性, 我们适当降低了非关键字结点权重在SLCA的重要程度中所占的比重, 每个SLCA的重要程度即可表示为:

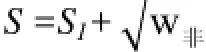
其中, S1表示为所有关键字结点的重要程度的总和.

4.3 排序算法

SLCA的重要程度可以反映出用户对该SLCA的偏好程度, 在查询结果中SLCA的重要程度越高就越符合用户的查询意图, 应该将该查询结果优先返回给用户. 本文使用基于关键词权重并结合结构关系的排序算法—WS-Rank算法, 通过排序算法对SLCA的重要程度进行统计计算, 并根据SLCA重要程度的计算结果对所有的SLCA进行排序, 排序算法的目标就是使得重要程度高的查询结果优先返回给查询用户. WS-Rank算法如算法2所示.

算法2. WS-Rank算法输入: 权重关系树Ti; 关键词权重Wi输出: 顺序SLCAs链表for each TiT do{∈{ TiTraversal(Ti);//遍历Ti关系树

由每个结点的重要程度统计每个Ti的重要程度; if 两个结点是father-childhood关系

father←a*childhood* Wi // 为每个关键词的权重值

else if ancestor-offspring .//祖先-后代关系

ancestor←b*offspring* Wi.

计算所有非关键字节点的重要程度之和;

根据SLCA的重要程度降序排列成链表

返回给用户顺序SLCAs链表 .//END

5 实验

实验是在一台Intel(R) Core(TM) i3-2310M CPU @ 2.10GHz, 4.00GB内存, 500GB硬盘和Windows 7操作系统的PC机上进行的, 基于数据集BookDB.xml,针对本文提出的排序方用Java语言和eclipse3.0编译工具借助Stack算法建立了XML关键字查询系统, 对排序方法进行验证.

评价XML关键字查询的一个重要指标是准确率.准确率(Precision)是指查询结果中与用户真实查询意图相关的元素所占总元素的比率[6]. 实验中, 通过查询系统对提出的排序方法进行测试, 并调查该系统用户的使用情况, 验证基于关键词权重的XML关键字查询结果排序方法的准确率. 验证实验邀请了5位测试者, 根据各自的需求和偏好, 在BookDB.xml上分别进行关键字测试查询(见下表1).

表1 数据集上的5条测试查询

完整的BookDB.xml数据集H中包含了大约50000个不同的元素, 从中查找所有与测试者真实查询意图相匹配的元素工作量太大. 因此, 我们在查询测试时使用了抽样数据集, 抽样数据集Hi是从完整数据集中随机抽取100条元素组成的, 实验阶段只需将在数据集Hi上的查询排序结果与测试者在数据集Hi中标示出的满足真实查询意图的记录结果作对比. 值得注意的是, 对于本文排序方法, 如果排序后结果中与用户查询意图相同的元素数量越多, 则排序算法的准确率就越高.

在权重关系树中使用WS-Rank算法对关系树中关键字之间的结构关系和结点的权重进行量化可以得到SLCA结点的重要程度, 进而得出查询结果的重要程度. 本次试验设定R=0.8(0＜R≤1), 由于0＜b＜a＜1, a2＜b, 通过计算可以对比每个权重关系树的重要程度大小即SLCA结点的重要程度, 因此我们以SLCA的重要程度为依据对所有的SLCA进行排序, 重要程度高的查询结果优先返回给用户.

将在数据集Hi上的经查询排序后得到的前10个返回结果与测试者在数据集Hi中标示出的前10个满足真实查询意图的记录结果作对比, 实验结果见表2.准确率可以用得到的两类结果数的比率表示, 即:

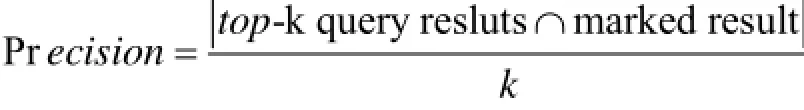
表2 Stack算法与本文排序结果准确率的对比

为更形象具体表现排序算法的查询的准确性, 我们将Stack算法所得的结果与WS-Rank排序算法的查询结果准确率作对比的柱状图如图3所示.

图3 Stack算法与本文排序方法准确率的对比

对比表2和图3的实验数据, 经过排序算法处理后返回的查询结果与Stack算法直接得到的查询结果的准确率相比, 查询结果的准确率得到了明显的提高,能够更好地反映用户的查询意图.

6 结语

本文提出了一种基于关键词权重并结合关键字结构关系的XML关键字查询结果排序方法. 该方法首先是通过Stack算法求解SLCA, 将得到的结果SLCA经过RTW算法处理后得到权重关系树, 根据权重关系树中结点的权重值和关键字之间的结构关系以及量化每个SLCA的重要程度, 并以此为依据对所有SLCA进行排序, 返回给用户有序的排序结果. 最终的实验结果证明, 本文提出的WS-Rank排序方法能够有效提高关键字的查询的准确率. 更深入的研究主要是在提高结果排序的效率的同时如何考虑用户的偏好, 考虑到用户偏好的结果排序方法能够更好地满足用户的查询需求.

1 任建华,周建,孟祥福,等.基于关键字之间结构关系的XML查询结果排序方法.计算机科学,2013,40(6):178–182.

2 Guo L, Shao F, Botev C, et al. XRANK: Ranked keyword search over XML documents. ACM SIGMOD International Conference on Management of Data. ACM. 2003. 16–27.

3 Mamou J, Kanza Y, Cohen S, et al. XSEarch: A semantic search engine for XML. International Conference on Very Large Data Bases-Volume. 2003. 45–56.

4 Li GL, Ooi BC, Feng JH, et al. EASE: An effective 3-in-1 keyword search method for unstructured, semi-structured and structured data. ACM SIGMOD International Conference on Management of Data. ACM. 2008. 903–914.

5 Bao Z, Ling TW, Chen B, et al. Effective XML keyword search with relevance oriented ranking. IEEE International Conference on Data Engineering. IEEE Computer Society. 2009. 517–528.

6 Li J, Liu C, Zhou R, et al. Suggestion of promising result types for XML keyword search. International Conference on Extending Database Technology. ACM. 2010. 561–572.

7 Liu Z, Cai Y, Shan Y, et al. Ranking Friendly Result Composition for XML Keyword Search. Conceptual Modeling. Springer International Publishing, 2015.

8 刘喜平.QWS-Rank:一种新颖的XML关键词搜索结果排序方法.小型微型计算机系统,2014,(12):2681–2685.

9 孟小峰.XML数据管理.北京:清华大学出版社, 2009.

10 Xu Y, Papakonstantinou Y. Efficient keyword search for smallest LCAs in XML databases. ACM SIGMOD International Conference on Management of Data. ACM. 2005. 537–538.

11 陆嘉恒.XML数据查询和检索技术.北京:清华大学出版社,2013.

Results Ranking Method of XML Search Based on Keyword Weight

WEI Dong-Ping, YUAN Zhi-Peng
(College of Computer and Communication Engineering, China University of Petroleum, Qingdao 266580, China)

A very important reason for low quality results of XML keyword searching is that it is difficult to reflect the user’s query intent. In this paper, setting keywords weight could resolve this problem to a certain extent. A new method of query results sort based on keywords weight and keywords structure is proposed. This method sets keywords weight and sets nodes weight for every node that contains keywords, according to keywords weight. The importance of the SLCA node is estimated according to the nodes weight in the relation tree and the relationship between keywords. The query results are sorted on the importance of SLCA nodes. The experimental results show that the proposed method has higher accuracy for sorting.

XML; keyword search; keyword weight; results sort

2016-07-16;收到修改稿时间:2016-08-18

10.15888/j.cnki.csa.005683