面向地质导向的三维井筒可视化①

魏 佳, 段友祥, 李 卿, 孙歧峰, 李洪强(中国石油大学(华东) 计算机与通信工程学院, 青岛 66580)(中石化胜利油田 钻井工艺研究院, 东营 57000)

面向地质导向的三维井筒可视化①

魏 佳1, 段友祥1, 李 卿1, 孙歧峰1, 李洪强21(中国石油大学(华东) 计算机与通信工程学院, 青岛 266580)2(中石化胜利油田 钻井工艺研究院, 东营 257000)

随钻地质导向是目前复杂油气藏开发的高端应用, 三维井筒可视化是其关键基础技术之一. 基于随钻获得的井斜工程数据和测井地质属性数据, 研究了建立均径井筒和非均径井筒模型的方法, 采用成像原理实现了地质属性的可视化表达, 并实现了井筒模型和地层可视信息的有机融合, 即在井筒壁上显示钻遇地层的属性信息. 基于OpenInventor对该方法进行了原型实现, 实际运行测试表明, 系统能形象、直观、准确地从井筒中观察钻遇地层情况, 为随钻地质导向的实现奠定了基础.

地质导向; 井筒; 井轨迹; 测井

随着油气勘探开发形势的不断发展和开发规模的不断扩大, 可供开发的常规油气资源日益减少, 小油层、断块油层、薄油层和老油田衰竭剩余油藏等复杂油藏勘探开发越来越受到重视[1]. 地质导向钻井已经成为复杂油气藏开发的重要手段. 地质导向钻井融合了钻井、测井、油藏地质以及计算机等多项技术, 通过采集和处理钻井工程数据和钻遇地质属性数据, 监测和控制钻进轨迹[2-4].

三维井筒建模和可视化是地质导向技术的基础和关键. 通过绘制三维井筒, 并在井壁上展示钻遇地层的属性, 可以直观地观察到井体随钻进的变化以及钻遇地层情况, 从而有效地控制井轨迹的着陆和走向.过去以“线”状表示的钻井轨迹没有对“井筒”进行三维建模[5,6], 有一些研究实现了井筒的立体效果, 但没有在此基础上添加显示地层、岩性等信息[7,8], 因此, 离随钻地质导向的实际要求差距很大.

1 井轨迹空间坐标计算

在钻井过程中, 井轨迹的空间状态一般以井口坐标系O-NEH来描述, 即井口位置(坐标原点O), 正北方向(N轴)、正东方向(E轴)和垂深(H轴), 如图1. 通过安装在钻头附近的测斜仪, 每隔一定的井段长度采集井深、井斜角、方位角等数据刻画目前钻头的钻进状态(称为测点). 假设有测点M, 其井深(也称为斜深)为从井口O到测点M的井轨迹长度L, 井斜角为M点的切线在钻头前进方向与重力线O1O2的夹角α, 方位角为正北方向顺时针旋转到M点在平面ONE上的投影线OO1上所转过的夹角Φ[9]. 见图1.

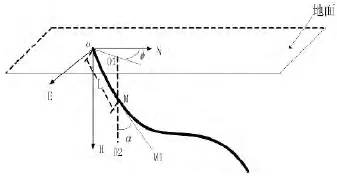
图1 井轨迹坐标系

关于如何由测斜仪测得的数据计算得到准确刻画井轨迹的空间坐标, 基于不同的假设模型, 目前国内外已经提出20多种计算方法. 常用的有: 以直线为模型的平均角法和平衡正切法、以圆柱螺线为模型的曲率半径法和校正平均角法、以空间圆弧为模型的最小曲率法和弦步法[10]等. 在比较各种方法的基础上, 本文采用了最小曲率法[11]. 即由测点的井斜数据(井深L、井斜角α、方位角Φ), 根据公式(1)到(5)分别求出测点的井深增量ΔD和北、东坐标增量ΔN、ΔE. 从而得到整个井眼轨迹的各测点的空间坐标.

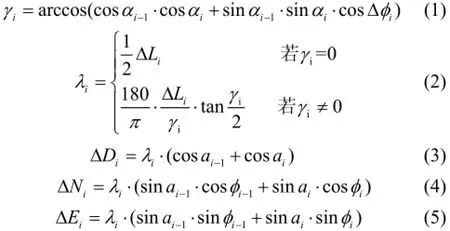
其中, αi-1, αi, Φi-1, Φi分别为上、下两测点的井斜角和方位角; ΔΦi, ΔLi分别为上、下两测点的方位角之差和井深之差.

2 三维井筒模型构建

三维空间模型的构建一般要根据场景对象的空间几何拓扑结构, 对不同特征的对象采用不同的构建方法. 对于规则形体对象, 可以直接用点、线、面等基本图元进行建模; 对于规则曲面形体对象, 可以使用球体、圆柱体等三次曲面进行建模; 对于非规则的曲面,则一般采用切片、角点网格等更灵活方法进行建模.

理论上, 若钻井过程中钻头不变, 井筒井径是均匀的. 但实际情况下, 由于钻遇地层的属性不同, 钻头钻进的角度不同以及发生泥浆侵蚀等, 井径会产生变化. 随钻地质导向钻井中, 如果从宏观上只考虑井筒的整体走势, 不考虑井径的变化, 井筒是一个规则的曲面形体对象, 可以采用简单的圆柱体拼接进行建模; 如果关注井筒的细节变化, 进行更加精细的井筒建模, 需要实时获得井径数据, 而井筒就属于非规则的曲面形体对象, 可以采用切片进行建模.

2.1 圆柱体拼接法

基本思想是: 以井轨迹上相邻两个测点的连线为垂线, 以这两个测点为上、下圆的圆心, 在两个测点间建立圆柱体, 然后将各个圆柱体拼接到一起, 形成井筒模型. 如图2所示.

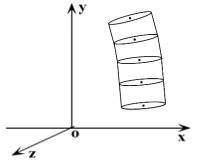
图2 圆柱体拼接法示意图

假设, 井筒半径为r, 井轨迹任意两个相邻测点的空间坐标分别为Pi(xi,yi,zi), Pi+1(xi+1,yi+1,zi+1), P点为Pi、Pi+1的中点, 如图3.

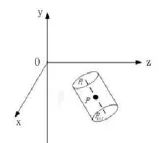
图3 两测点之间的圆柱体

具体建模过程如下:

1) 计算圆柱体的高度, 绘制以原点为轴心的圆柱体.

首先, 计算圆柱体高度D, 见公式(6):

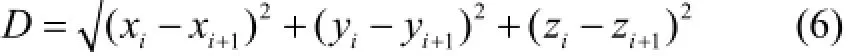
然后, 绘制以原点O为轴心, y轴正方向为中轴线, r为上、下圆半径, D为高度的圆柱体cy1, 如图4(a).

2) 将圆柱体cy1的轴心移动至Pi、Pi+1的中点P处.

得到旋转轴和旋转角度之后, 执行坐标变化进行旋转, 得到圆柱体cy3, 如图4(c).

4) 从第一个测点到最后一个测点, 依次重复前面3个步骤, 得到整个井筒模型.

圆柱体拼接法构建三维井筒算法简单, 易于实现,但是对于弯度较大的井和非均匀井径的井建模不够精确.

2.2 切片法

基本思想是: 以井轨迹作为中轴线, 以井轨迹上的每个测点为圆心绘制圆, 每个圆看作是井筒的一个切片, 在每个圆上取适量的等分点, 并将相邻两个圆上的等分点进行连接, 形成基于四边图元或三角图元的面, 最终构成无缝的井筒[8]. 如图5所示.

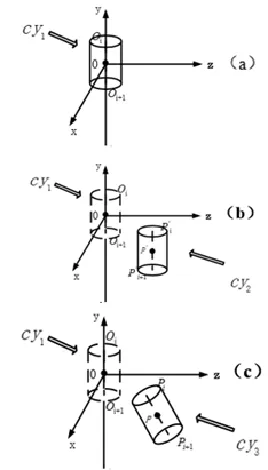
图4 圆柱体绘制过程图

图5 切片法示意图

假设井眼轨迹上相邻两个测点Pi、Pi+1的坐标分别为(xi,yi,zi), (xi+1,yi+1,zi+1), Pi、Pi+1测点处已知的井径分别为di, di+1. 具体建模过程如下:

1) 求取以Pi+1为圆心的切片圆周上等分点的局部坐标Q′(x′,y′,z′).假设测点Pi+1为局部坐标系的坐标原点, 向量的方向为局部坐标系y′轴正方向. 以局部坐标x′轴正方向与切片圆pi+1相交处为起点, 沿逆时针方向将切片圆pi+1进行n等分. 如图6所示, 整个圆周的角度为2π, 则每等份的夹角为: 2π/n. 可得Q′的局部坐标值计算公式(9).

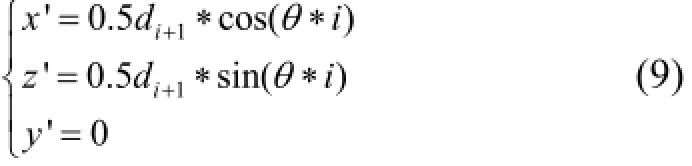
其中i∈(0,1,2,…n-1), θ=2π/n.

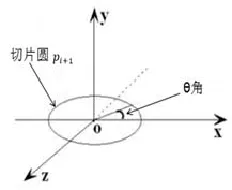
图6 经过平移与旋转后的切面

2) 将切片圆pi+1上等分点的局部坐标Q′(x′,y′,z′)转换为全局坐标Q(x,y,z)

首先切片圆pi+1沿全局坐标轴(x、y、z轴)分别平移(xi+1,yi+1,zi+1), 将圆心O移至Pi+1点位置; 然后, 将切片圆pi+1绕x轴顺时针旋转α角, 绕z轴顺时针旋转β角, 使切片圆pi+1过圆心的法向量与向量的正方向相同, 如图7. 经过以上平移和旋转操作后, 可得到切片圆pi+1上等分点的局部坐标转换为全局坐标的关系公式(10).

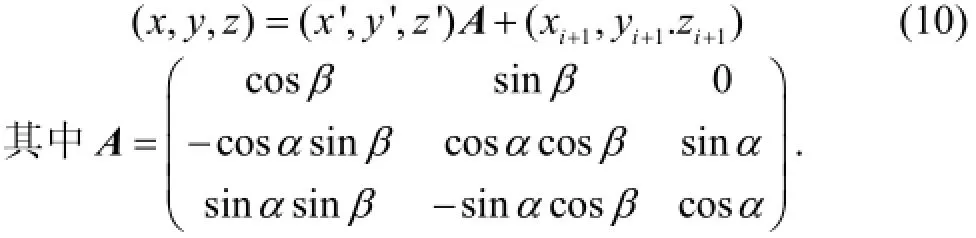
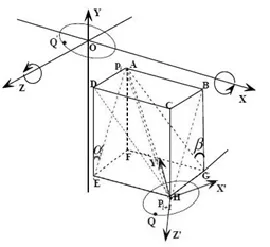
图7 坐标转换图

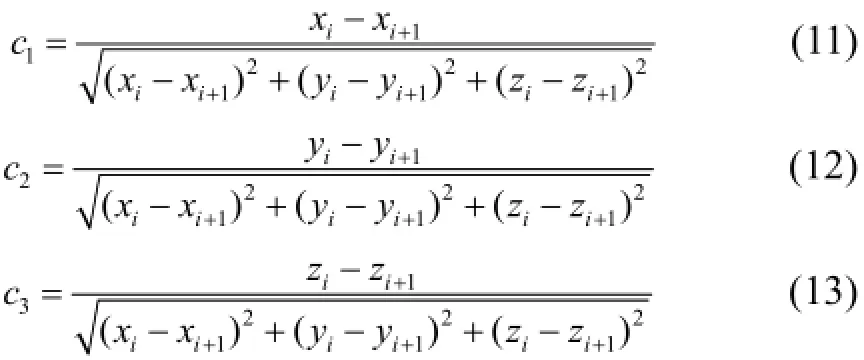
根据余弦值不同可将公式(10)表示为以下三种形式, 见式(14)、(15)、(16).

3) 构建切片圆之间的侧面

将相邻两个切片圆上的等分点进行连接, 形成基于四边图元或三角图元的面, 最终构成无缝的井筒,如图8所示. 假设切片圆pi对应的n个等分点为Pi0, Pi1……Pin.

采用四边面片构建井筒模型的具体过程如下:

从点P00开始, 依次加入P01、P10和P11, 顺次连接P00、P01、P10和P11形成第一个四边形. 然后加入P02、P12, 同样顺次连接P01、P02、P11和P12形成第二个四边形, 依此类推, 每次从两个切片圆上各加入一个点,与前两个点连接为一个四边形, 直至加入最后一个点,完成第n个四边形的连接, 从而完成了p0, p1两个相邻切片圆的侧面构建. 从切片圆p0, p1一直到pn将所有相邻的两个切片圆都按相同的方法进行处理就得到了整个井筒的模型.

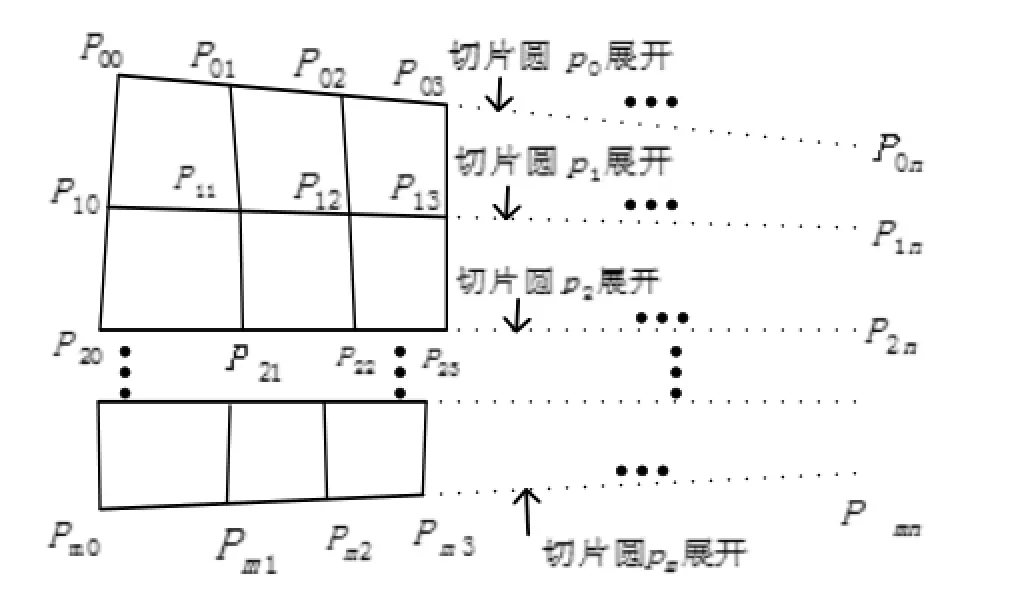
图8 四边形面片构造井筒示意图

类似地, 也可以使用三角面片作为基本图面构造井壁面, 具体不再赘述.

图9是用不同方法构建的井筒模型截取相同深度的一段示意图, 其中图9(a)是用三角面片构建的井筒模型, 图9(b)是采用四边形面片构建的井筒模型.

三角面片比四边形面片更利于复杂三维模型的构建, 但是计算量也更大. 对于相对简单的井筒模型,一般采用四边形面片来构建就能满足要求, 而且效率高.

图9 不同方法构建的井筒模型

3 地层信息可视化

井筒模型建立后, 通过井筒观察到钻遇地层的情况是可视化的最终目标. 在随钻过程中, 通过随钻测井可以获得钻遇地层的地质属性数据, 比如电阻率、自然伽马、自然电位、岩性密度等, 这些地质属性数据可以反映出钻遇地层的情况[12], 因此, 需要将这些地质属性数据进行可视化, 再与建立的井筒模型进行融合, 从而达到了在三维井筒的井壁上浏览(漫游观察)钻遇地层情况的可视化效果.

经过分析和研究, 地质属性的可视化采用成像来实现, 然后把成像映射到井筒模型的井壁上. 本文以随钻自然伽马测井数据为对象, 数据包括了环绕井周测得的8组伽马测井数据.

3.1 数据预处理

由于随钻方位伽马测井所测得的数据是井周不连续的8个测点测得的, 因此首先需要进行插值处理,得到井周360度方位上完整的伽马数据然后才能成像.以每个地层深度上的8个数据作为基本数据, 通过插值获得区间为[0º,360º]内的数据.

假设某一深度上的八个伽马数据为: GR0、GR1……GR7, 该深度上的一组观测值记作(xi, yi), 其中i∈(0,1,2,…8), xi表示方位, 即从正北方向旋转过的角度, yi表示该方位处的伽马值.

于是有xi=i×45º;当i＜8时, yi=GRi;当i=8时, yi=GR0.

插值方法选择经典的三次样条插值[13,14]. 设在插值区间[a,b]上, 有n+1个节点x0, x1, x2…xn, yi=f(xi), 其中a=x0＜x1＜ x2＜…＜xn=b. 则三次样条插值函数S(x)必须满足以下条件:

①在每个区间[x1, x2]上, S(x)是三次多项式, i=(0,1,2,…n-1);

其中ai, bi, ci, di代表4n个未知系数.

另外还必须给出三次样条函数的边界条件. 经比较选择满足自然边界条件, 三次样条函数在端点处的一阶导数与原函数一阶导数相同, 并已知导数值, 即S′(x0)=f ′0, S′(xn)=f ′n.

由已知条件和边界条件求出三次样条函数的未知参数, 将每个深度上的8个初始观测值代入, 完成[0º,360º]区间上的插值, 得到井周360度方位上完整的伽马数据.

3.2 测井数据成像

经过数据预处理得到井周360度方位上的伽马数据后, 按照一定的映射规则转换成一组像素颜色值,生成伽马测井成像图.

1) 定义色谱. 伽马成像常用的色谱标准是以黄色为主, 从白色过度到黑色. 生成的128级色谱如图10.

图10 128级色谱

2) 建立映射规则. 确定伽马数据和RGB颜色值的对应关系, 常用的方法有静态映射和动态映射两种.

静态映射:根据整个井段上的所有伽马数据来建立映射规则, 该映射方法能反映整个井段伽马值的变化趋势. 算法如下:

①找出整个井段中伽马数据的最大值和最小值,分别表示为γmax, γmin;

②计算伽马值和色标值的对应比例关系:

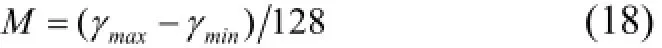
③ 计算得到伽马数据γi对应的色标:

④ 整理公式(18)和(19)得到色标计算公式(20):

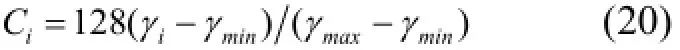
其中γi为某个伽马值, Ci为伽马值经映射后得到的色标值.

动态映射: 该方法主要针对有限的颜色刻度与全井段大范围伽马值变化之间的矛盾而提出的. 基本思想是将整个井段进行分段处理, 每段分别应用静态映射法.

3) 成像. 以纵坐标表示深度, 横坐标表示方位,将每个计算得到的像素值在对应的深度和方位显示出来, 便可生成最原始的成像图(即位图). 为了克服位图的不足, 采用如下的策略进行处理: 将原始成像图中每相邻的四个像素点连接成一个四边形, 并且保持每个像素点的颜色值不变. 给四边形的四个顶点赋上颜色值, 内部以颜色渐变的方式进行填充[15]. 这样生成的成像图具有矢量特征, 且不影响生成效率. 图11(a)是使用静态映射的方法生成的整个井段的伽马成像图,图11(b)是使用动态映射的方法生成的整个井段上的伽马成像图. 可以明显看出, 动态映射的方法可以更清晰的观察地层变化情况, 而静态映射更利于观察整个井段上的变化趋势.

图11 伽马成像图

3.3 井筒模型与成像的融合

实现井筒模型和成像图的有机融合, 即把成像表示出来的地质属性展示在井筒上, 最终完成井筒的三维可视化.

融合采用了纹理映射技术, 以测井成像图作为纹理, 把井筒模型作为空间中的三维物体, 具体过程为:

1) 求出构建井筒的各切片圆的等分点对应在伽马成像图上的纹理坐标.

2) 将纹理坐标对应的纹理像素值赋给切片圆的等分点.

3) 以赋了像素值的切片圆等分点作为顶点进行四边形连接, 内部以渐变的方式进行填充完成测井成像图渲染.

图12是利用两口井的实际数据进行井筒建模和地层属性可视化的最终效果. 其中井(a)具有均匀井径,井(b)具有非均匀井径.

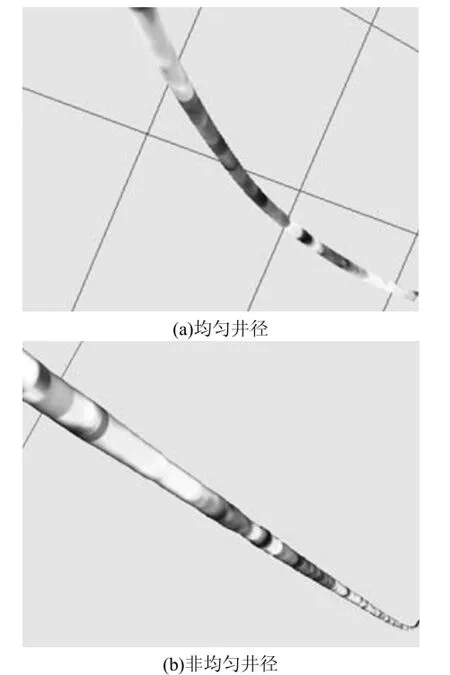
图12 最终效果图

4 结语

基于复杂油气藏勘探开发中随钻地质导向技术应用的迫切需求, 研究了对钻井工程轨迹进行了三维井筒建模的方法, 使简单的“点轨迹”变为立体的“井筒”,非均井径的井筒能更准确直观的表示钻井工程的实际过程, 也为通过井筒观察或展示钻遇地层信息开辟了途径. 同时对钻进过程中获取的地质属性数据以成像的形式进行可视化, 通过纹理映射到井筒体上, 实现了井筒模型和地质属性可视信息的融合, 真正实现了井筒的三维可视化, 为地质导向技术的应用奠定了坚实的基础.

1 荣海波,贺昌华.国内外地质导向钻井技术现状及发展.钻采工艺,2006,2:7–9,121.

2 杨雪,潘保芝,汪凯斌,等.随钻方位伽马测井快速正演及定向井动态监测.地球物理学进展,2016,(1):403–410.

3 刘旭.页岩气水平井钻井的随钻地质导向方法.天然气工业, 2016,36(5).

4 王智锋.MRC近钻头地质导向系统总体设计与应用.石油钻采工艺,2015,(4):1–4.

5 陈刚,杨雪,潘保芝,等.井眼轨迹计算及可视化研究现状.世界地质,2015,34(3):830–841.

6 张洋弘,孙歧峰,邵尉,等.基于Web的三维实时井眼轨迹可视化方法研究与实现.微型机与应用,2015,(16):74–76.

7 黄志强,李洋,郑双进.基于井筒切片技术的三维井眼轨迹软件的设计与实现.录井工程,2013,24(2):67–69.

8 张敏.石油钻井井眼轨迹三维可视化建模.电脑知识与技术, 2011,7(13):3182–3183.

9 刘修善.井眼轨迹的弯曲与扭转问题的研究.钻采工艺, 2007,30(6):30–34.

10 王志军,杨涛,徐森,等.基于OPENGL的井眼轨迹三维可视化系统的实现.录井工程,2015,26(1):73–75.

11 曹传文,薄珉.最小曲率法井眼轨迹控制技术研究与应用.石油钻采工艺,2012,34(3):1–6.

12 杜志强,郝以岭,张国龙,等.方位伽马随钻测井在冀东油田水平井地质导向中的应用.录井工程,2008,19(1):18–21.

13 符祥,郭宝龙.图像插值技术综述.计算机工程与设计,2009, 30(1):141–144.

14 侯云山,刘宏兵.三次样条函数的计算机求解.中州大学学报,2004,21(3):111–112.

15 Wernecke J. The Inventor Mentor: Programming Object-Oriented 3d Graphics with Open Inventor, Release 2nd ed. Addison-Wesley Longman Publishing Co. Inc. 1993: 130–320.

3D Visualization of Wellbore for Geosteering

WEI Jia1, DUAN You-Xiang1, LI Qing1, SUN Qi-Feng1, LI Hong-Qiang21(College of Computer and Communication Engineering, China University of Petroleum, Qingdao 266580, China)2(Drilling Technology Research Institute of Shengli Oilfield, SINOPEC, Dongying 257000, China)

Geosteering while drilling is a high-quality application of complex reservoirs development, and 3D visualization of wellbore is one of the essential and indispensable technologies for it. The methods of modeling wellbore which have equable or unequable radius are researched, and the visualization of geological properties is achieved by using imaging principle, based on the well inclination data and well logging data getting from LWD. Then the 3D wellbore model and the imaging information would be combined together, which means showing the drilling stratum attributes in the wall of the wellbore. A system model is implemented based on OpenInventor, of which running tests show that attributes of drilling stratum from wellbore can be observed vividly and accurately, and it laies a solid foundation for the implement of geosteering while drilling.

geosteering; wellbore; well trajectory; well logging

2016-07-26;收到修改稿时间:2016-09-13

10.15888/j.cnki.csa.005729