基于不完备信息系统的灰度优势粗糙近似模型①

胡明礼, 丁 磊(南京航空航天大学 经济管理学院, 南京 211106)

基于不完备信息系统的灰度优势粗糙近似模型①

胡明礼, 丁 磊
(南京航空航天大学 经济管理学院, 南京 211106)

为解决不完备信息的偏好决策问题, 多种优势关系及其相应的粗糙集模型被提出并证实其实用性. 然而在实际情况中, 只要存在缺失值那么无论使用何种方法对比出来的优势关系都存在一定的不确定性. 基于此, 本文分析了影响灰度大小的因素, 定义了优势关系中灰度和差异系数的概念并给出了计算方法, 建立了两对象间进行对比的灰度度量. 提出了基于灰度的优势关系及其粗糙集近似模型. 与广义扩展优势关系和扩展优势关系相比, 基于灰度优势关系的粗糙集模型近似分类精度和质量均有提高. 最后通过实例证明了灰度优势关系及其粗糙近似模型的实用性.

不完备信息系统; 灰度优势关系; 粗糙集; 广义扩展优势关系

1 引言

由于环境的复杂性、人类计算能力和认知能力的局限性、信息的不对称性, 人们做出的决策并非完全理性的, 即存在一定的不确定性. 针对模糊信息和不明确表述, Pawlak等[1]最先提出了粗糙集理论来对不精确或不确定的知识进行近似描述和处理. 为了解决偏好序问题, Greco等[2-4]拓展了传统粗糙集中对象间的二元关系, 在不可分辨性的基础上提出了二元优势关系. 何亚群等[5]提出了扩展优势关系的概念, 将粗糙集方法从完备信息系统拓展到不完备信息系统中. 胡明礼等考虑到可比较信息的多少对分类准确性的影响,认为不具有共同非空属性的两个对象在扩展优势关系中进行对比时误分类的几率非常大. 基于这种观点,文献[6]以共同非空属性个数是否为0为衡量指标, 对可比较信息多少进行了限定, 提出了基于有限扩展优势关系的粗糙集决策方法. 在此基础上, 胡明礼[7]提出, 当条件属性较多的时候, 通过限定共同非空属性个数是否为0并不能很好的反映可比较信息的多少, 条件过于宽松. 于是便提出了基于广义扩展优势关系的粗糙决策方法. 通过设定阈值的方法来限定可比较信息的多少. 然而只要存在缺失值, 那么无论对比的方法多么科学, 也必然存在误分类的情况, 优势关系都具有不确定性. 现有的优势关系粗糙集模型仅对可比较信息多少做出限定, 考虑不够全面. 同时并没有对两对象间优势关系的不确定性大小做出明确的区分.如何处理不完备信息系统下优势关系不确定性问题仍需进一步研究.

在传统粗糙集方法中部分学者通过将粗糙集与灰色系统相结合的方法来处理不确定问题. Yamaguchi[8]使用灰色粗糙集模型中的灰格关系代替了粗糙集中的不可分辨关系提出了基于灰格的灰色粗糙集模型. 此外,该模型还存在一定的不足,它以灰格一致关系为基础,在对两个对象进行分类的时候显得条件过于苛刻.因此, Yamaguchi[9]等人又提出了以灰格包关系为基础的灰色粗糙集模型,较基于灰格一致关系的灰色粗糙集模型在分类限制条件上做了一定的改进. 王天擎等[10]认为Yamaguchi提出的模型中单个属性的上近似集仅仅根据两个对象值相交不为空就被认为是处于同一类中, 这种条件显得过于宽松; 而下近似集则要求两个对象具有包含关系, 可能使得这两个对象值绝大部分相同却不能分在同一类中这种条件又过于严苛. 因此,他提出了一种基于可变精度分类的变精度灰色粗糙集模型. 赵焕焕等[11]利用灰色相似关联度定义基于阈值的灰色相似关联关系, 并用灰色相似关联关系代替粗糙集中的不可分辨关系, 很好地克服属性值离散化处理过程中容易造成一定程度的信息损失问题.

借鉴以上研究, 本文将灰度概念引入到优势关系粗糙集中. 通过对优势关系中不确定因素的分析, 结合齐当别[12]模型中的观点, 本文认为优势关系的不确定性除了与信息多少有关以外, 还与属性的重要性以及属性值差异大小有关. 以此为基础, 构建灰度度量,建立灰度优势关系, 并运用灰数分级理论对优势关系粗糙集作进一步拓展.

2 理论基础

定义1. (不完备有序决策系统)[5]在决策系统S=(U, A, V,f）中U代表论域; A代表属性集合, A=C∪D, C代表条件属性, D代表决策属性; V代表属性的值域, VC代表条件属性的值域, VD决策属性的值域, 值域具有偏好次序; f: U×A→V代表一个信息函数, 表示对每一个x∈U, q∈A, f( x, q)∈Vq, 如果存在某些属性值Vq*∈Vc等于空值“*”, 则S称为不完备有序决策系统.

定义2. (二元关系)[13]R为集合A上的二元关系(1) 若∀x∈A，xRx 成立, 则称R是自反的; (2) ∀x，y∈A , x和y之间存在序关系, 若y≺ x 则x≻ y, 则称x, y间满足序对称性;

(3) ∀x, y, z∈A , 如果xRy, yRz, 那么xRz, 则称R具有传递性.

定义3, 4, 5均基于一个给定的决策系统S=(U, A, V,f），p⊆A, x, y ∈U

定义3. (扩展优势关系)

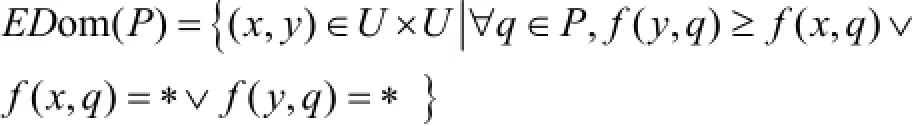
y优于x用yDpEDomx表示. 扩展优势将优势关系从完备信息系统扩展到不完备信息系统中.

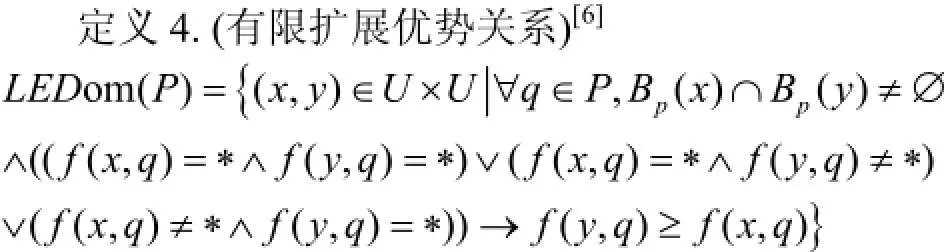
其中Bp, 表示不存在空缺值的属性. y优于x用yDLpEDomx表示. 有限扩展优势关系在扩展优势关系的基础之上作出限定Bp(x)∩Bp(y)≠Ø即共同非空属性的个数不为0.

定义5. (广义有限扩展优势关系)[7]

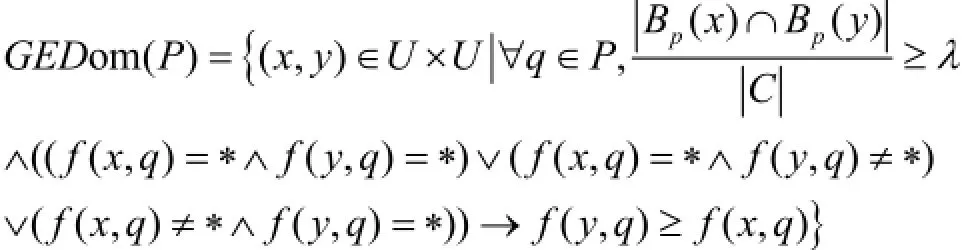
y优于x用yDGpEDomx表示. 广义扩展优势关系使用了一个阈值λ来限制非空属性与条件属性的个数比来对优势关系进行约束.

3 基于灰度优势关系的粗糙近似模型

3.1 影响灰度的因素

借鉴灰色系统中对灰度的定义, 本文将优势关系中灰度定义为某一对象优于或者劣于另一对象的不确定程度.

在不完备信息系统中, 优势二元关系的不确定性是普遍存在的. 两对象间优势关系的不确定性越大,即灰度越大, 那么将一个对象优于或者劣于另一对象判断错误的可能性越大, 误分类的情况也会随之发生.

(1) 信息的多少

苟光磊[14]认为, 人们更愿意使用信息更优更详细的数据. 两对象间进行对比时, 在不考虑其他因素的前提下, 两对象的不确定信息越少, 对比出来的优势关系确定性越大. 例如, 本文第5节应用实例中, 在判断供应商X1是否优于供应商X8时, 共同非空属性有3个; 而在判断供应商X10是否优于供应商X8时, 却没有共同非空属性, 所包含的确定信息远小于前者. 在不考虑其他因素的情况下, 前者所判断出的优势关系灰度小于后者, 确定性更大, 因而误分类的可能性越小.

(2) 属性权重

在实际应用中, 不同属性的重要度肯定是有差异的. 在部分数据表中, 少数重要度极大的条件属性在决策的过程中对决策结果起着至关重要的作用. 在不考虑其他因素的作用下, 当缺失值所在属性的权重越大, 该优势二元关系的不确定性越大, 即灰度越大.例如, 本文第5节应用实例中, 为了区分重要性的差异, 假定属性A1、A2、A3、A4的权重分别为0.3、0.1、0.1、0.5. 在不考虑其他因素的作用下, 当缺失值出现在A4中时, 灰度较大.

(3) 属性值的差异程度大小.

借鉴齐当别模型[12]中的思想, 人们在做决策的时候会人为地忽略差异小的属性, 而将差异大的属性作为最终的抉择依据. 单个属性的属性值差异越大, 那么这个属性对整体优势关系的影响越大; 差异越小,那么这个属性对整体优势关系的影响就越小.

综合考虑以上因素, 本文选取确定信息多少、属性权重和差异大小作为构建灰度度量的三个主要因素.

3.2 差异系数

为了区分属性值差异大的情况和属性值差异小的情况, 本文设定了一个差异系数.称为在属性q下, 对象x 优于对象x的差异mij系数.=1表示在属性q下, 对象x确定优于对象mix且属性值大小差异较大;=0表示在属性q下, jm对象xi与对象xj属性值大小差异较小, 可以忽略;不存在表示在属性qm下, 不能判断对象xi优于对象xj.由差异系数的定义可知, 通过α和ε的设定, 忽略属性值差异较小的情况, 从而建立一个差别机制, 将属性值差异大的情况和属性值差异小的情况进行了区分. 同时减弱了噪音数据的干扰, 使得模型整体具备一定的容差能力. 在不考虑其他因素的情况下, 属性值差异越大, 一个对象优于或者劣于另一对象的可能性就越大, 不确定性越小.

3.3 灰度

定义7. 对于xi, xj∈U,如果对象xi和对象xj中存在缺失值, 并且对于∀q∈■■Bp(xi)∩Bp(xj)■■,都有f( xi, q)≥f( xj, q), 那么灰度定义如下:

3.4 灰度优势关系

定义8. 对于一个给定的决策系统S=(U, A, V,f）, xi, xj∈U, P⊆A , 灰度优势关系GDR(P)定义为:

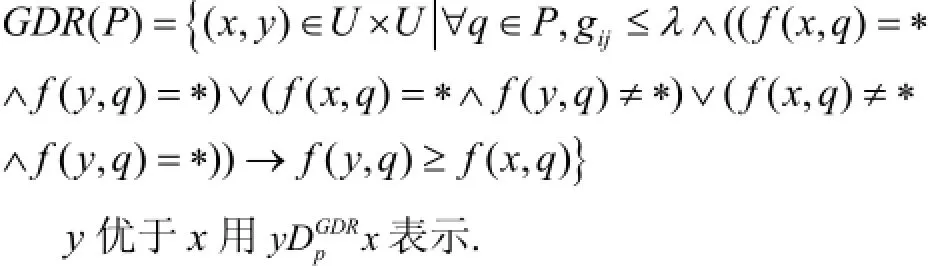
与广义扩展优势关系所设置的阈值不同的是, 灰度优势关系用灰度对优势关系的不确定性做了一个限定, 同时考虑了权重和属性值差异程度对分类的影响,更加符合在实际应用中所遇到的情况. 通过调整阈值的大小来确定对优势关系的约束力度, 从而有效地减小了因为不确定性差异而误分类的几率.

性质1. 灰度优势关系满足自反性和序对称性, 但不一定满足传递性.

性质2. 阈值λ的取值范围为［0,1］.

定义9. (灰度优势集、灰度劣势集)给定一个决策系统S=(U, A, V,f）,x∈U, 则对象x的灰度优势集(灰度劣势集)定义为:

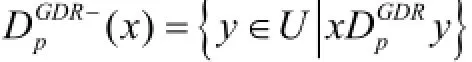
3.5 基于灰度优势关系的粗糙近似

定义10. 在决策系统S=(U, A, V,f）中, 对于P⊆A，x⊆U, Cl≥,Cl≤⊆U, t=1,2,…,n , 在灰度优势

tt关系下, 分别对上联合和下联合的粗糙近似作如下定义:

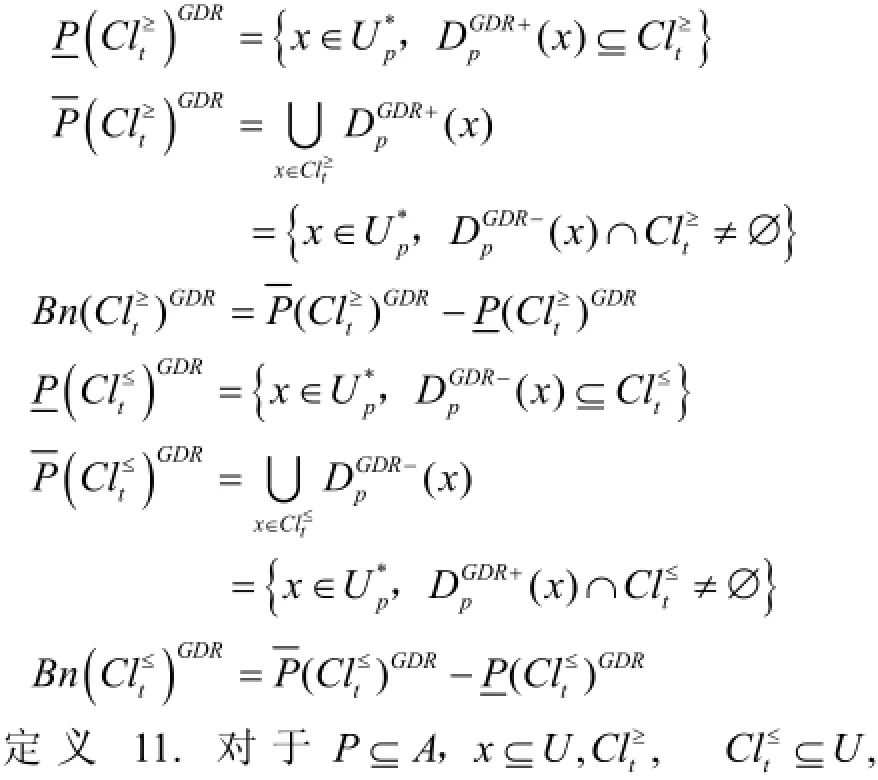
t=1,2,…,n在灰度优势关系下, 上联合和下联合的粗糙近似分类精度定义为:

4 几种优势关系粗糙集方法的对比

4.1 几种优势关系的对比

证明: 根据定义10中边界域Bn( Cl)GDR的概念以及

t定理1和定理2的结论可直接证得推论1.

4.2 几种基于拓展优势关系的近似分类性能对比

定理3. 三种优势关系近似分类精度对比:

证明: 根据定义11近似分类精度的定义以及定理1和定理2的结论可直接证得定理3.

定理4. 三种优势关系近似分类质量对比:

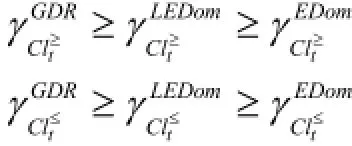
证明: 根据定义12中近似分类质量的定义以及定理1和定理2的结论可直接证得定理4.

5 应用实例

为证明灰度优势关系的实用性, 下面应用一个实例来进行说明. 表1是某公司下属供应商的信息表.属性A1, A2, A3, A4为条件属性, 分别代表了对供应商考核的4个指标, 表中1、2、3分别表示差、中、优. A5为决策属性, 表示对供应商的选择情况, 3表示选择该供应商, 1表示不选择该供应商, “*”代表空值. 为了凸显不同属性间重要度的差异, 本文假定属性A1、A2、A3、A4的权重分别为0.3、0.1、0.1、0.5. 同时假定α=0.2,ε=0.

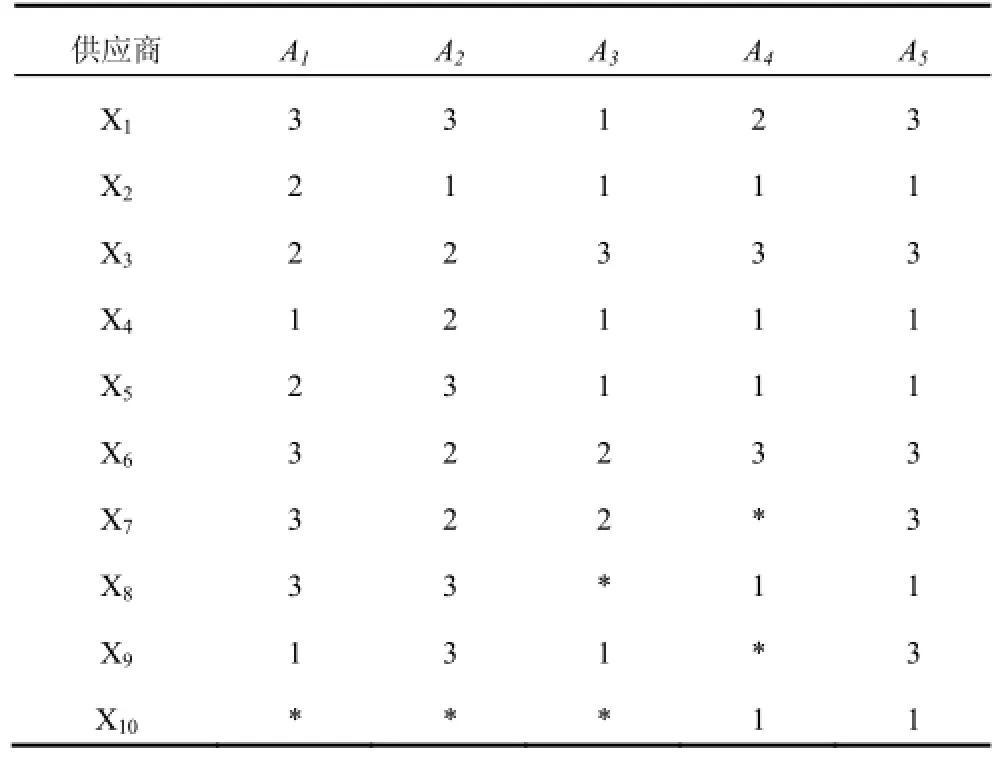
表1 某公司对供应商考核信息表

由表1, 我们可得如下信息:

A1, A2, A3, A4, A5均可视为偏好属性. A1, A2, A3, A4为条件属性, A5为决策属性.

在扩展优势关系下进行计算得如下结果:

上联合:

在广义扩展优势关系下进行计算得如下结果:

在灰度优势关系下, 借鉴灰数分级理论, 将灰数分成五级, 分别令λ=0.8,0.6,0.4,0.2, 计算得个对象间灰度大小如表2所示.

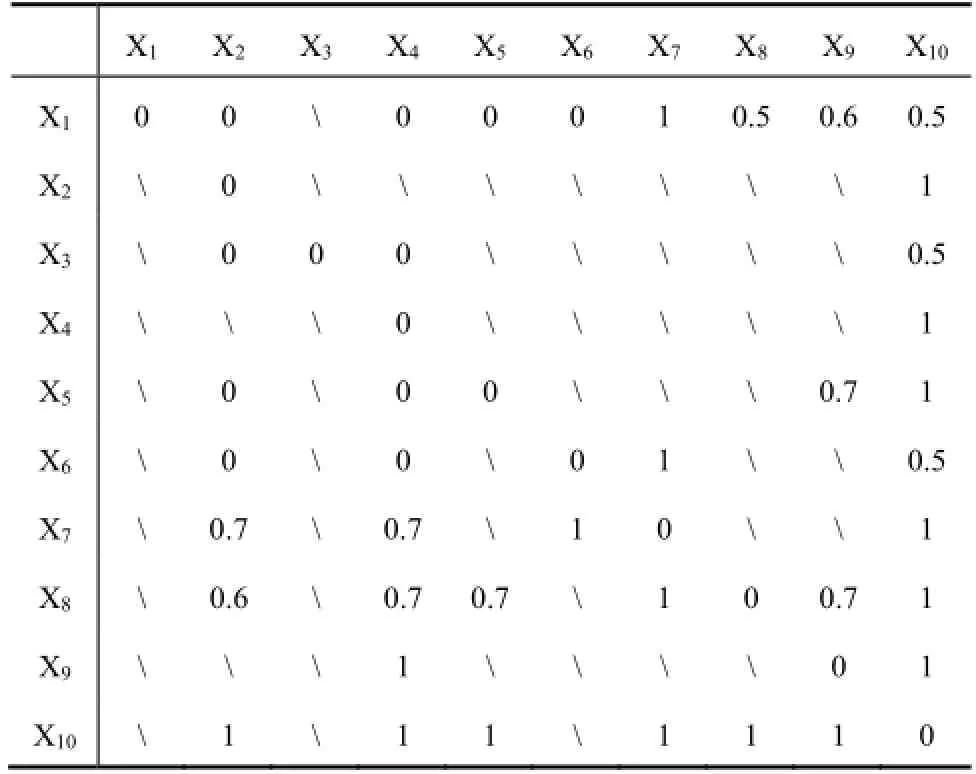
表2 灰度矩阵

为了便于理解, 表2中分别使用X1到X10代表编号为1到10的员工. 表中所计算出的数值代表行对象优于列对象的灰度.

运用三种优势关系Edom、LEDom、GDR所求出的近似分类精度和近似分类质量的计算结果如下:

上联合:

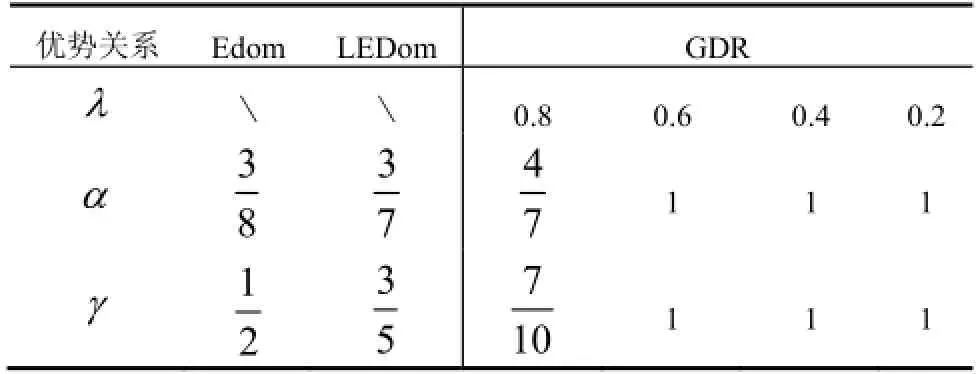
优势关系EdomLEDom GDR λ＼ ＼ 0.80.60.40.2 α33 7 1 1 1 4 87 γ137 10 1 251 1

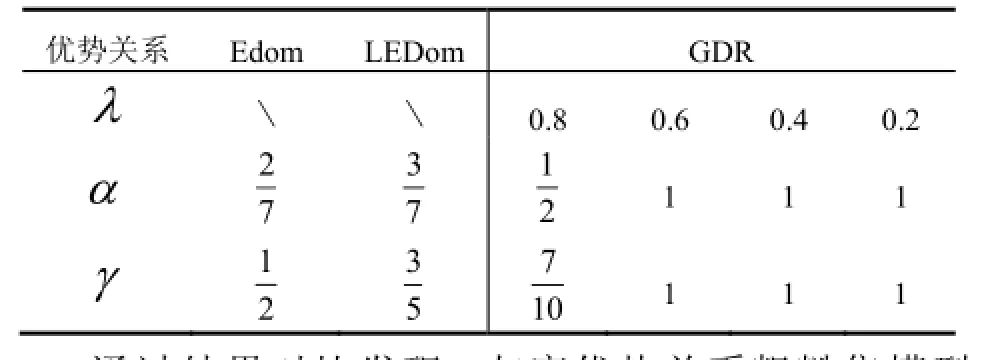
下联合:

通过结果对比发现, 灰度优势关系粗糙集模型(GDR)相比较广义扩展优势关系(LEDom)和扩展优势关系(Edom)所对应的粗糙集模型而言近似分类精度α和近似分类质量γ都有了一定的提高, 从而从实例的角度证明了定理3和定理4. 灰度优势关系在一定程度上可以减少因为不确定性太大造成误分类的情况.随着阈值的减小, 分类对确定程度的要求越来越高.

6 结论

本文提出的灰度优势关系是对不完全信息系统下优势关系的拓展, 在前者的基础之上加入了权重和差异程度的概念, 以此来构建灰度度量, 通过调整阈值的大小来减少因对象间优势关系的不确定性而造成误分类的情况, 使得计算结果更加符合实际. 通过证明和实例演算比较的结果, 灰度优势关系的粗糙近似方法具有更优的近似分类性能.

1 Pawlak Z, Skowron A. Rudiments of rough sets. Information Science, 2007, 177(1): 3–27.

2 Greco S, Matarazzo B, Slowinski R. Rough sets theory for multicriteria decision analysis. European J of Operational Research, 2001, 129(1): 1–47.

3 Greco S, Matarazzo B, Slowinski R. Generalizing rough set theory through dominance-based rough set approach. 10th International Conference on Rough set, Fuzzy Sets, Data Mining and Granular Computing. Heidelberg: Springer-Verlag. 2005. 1–11.

4 Greco S, Matarazzo B, Slowinski R. Dominance-based rough set approach to case-based reasoning. 3rd International Conference on Modeling Decisions for Artifical Intelligence. Heidelberg: Springer-Verlag. 2006. 7–18.

5何亚群,胡寿松.不完全信息的多属性粗糙决策分析方法.系统工程学报,2004,19(2):117–120.

6胡明礼,刘思峰.基于有限扩展优势关系的粗糙决策分析方法.系统工程,2006,24(4):106–110.

7胡明礼,刘思峰.基于广义扩展优势关系的粗糙决策分析方法.控制与决策,2007,22(12):1347–1351.

8 Yamaguchi D, Li GD, Nagai M. On the combination of rough set theory and grey theory based on grey lattice operations. International Conference on Rough Sets & Current Trends in Computing. 2006. 507–516.

9 Yamaguchi D, Li GD, Nagai M. A grey-based rough approximation model for interval data Processing. Information Sciences, 2007, 177(21): 4727–4744.

10 王天擎,李琪.基于灰格运算的变精度粗集模型及规则获取.统计与决策,2015,(2):22–25.

11 赵焕焕,刘勇,Jeffrey F,刘思峰.基于灰色相似关系的灰色变精度粗糙集模型及其应用.系统工程,2015,(2):146–151.

12 李纾,毕研玲,梁竹苑,孙彦,汪祚军,郑蕊.无限理性还是有限理性?—齐当别抉择模型在经济行为中的应用.管理评论,2009,21(5):103–114.

13 苗夺谦,李道国.粗糙集理论、算法与应用.北京:清华大学出版社,2008.

14苟光磊,王国胤,利节,吴迪.基于置信优势关系的粗糙集近似模型.控制与决策,2014,29(7):1325–1329.

Grey Rough Approximate Model Based on Incomplete Information System

HU Ming-Li, DING Lei
(College of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China)

Some scholars have already proposed a lot of dominance relation and corresponding rough models under incomplete information system in order to deal with the problem of preference decision which has incomplete information. It is uncertain that no matter use which method to contrast two objects as long as there is missing value. According to this defect, this article analyzes the factors that influence the gray scale, defines the concept of the gray and the difference coefficient in the dominance relation, and gives the calculation method and establishes an index to measure the degrees of the contrast between two objects. Therefore, the dominance relation based on grey system and its rough approximation model is presented. Through the comparison analysis, the precision and quality of the rough set model based on the grey dominance relation are improved. The given example proves the practicality and effectiveness of the grey dominance relation and its rough approximation model.

incomplete information system; grey dominance relation; rough sets; generalize extended dominance relation

国家自然科学基金(90924022,71171112);教育部人文社科基金项目(10YJC630084);中国博士后科学基金项目(2013M531356);江苏省基础研究计划(自然科学基金)--青年基金项目(BK20130786);江苏省博士后科研资助计划(1301106C);中央高校基本科研业务费专项科研项目(NS2011018,NN2012016,NJ20130020,NS2014085)

2016-07-07;收到修改稿时间:2016-09-23

10.15888/j.cnki.csa.005719