基于改进变分模态分解和Hilbert变换的变压器局部放电信号特征提取及分类

朱永利 贾亚飞 王刘旺 李 莉 郑艳艳

(新能源电力系统国家重点实验室(华北电力大学) 保定 071003)



基于改进变分模态分解和Hilbert变换的变压器局部放电信号特征提取及分类

朱永利 贾亚飞 王刘旺 李 莉 郑艳艳

(新能源电力系统国家重点实验室(华北电力大学) 保定 071003)

针对现有局部放电(PD)信号特征提取方法存在的不足，提出一种基于变分模态分解(VMD)和Hilbert变换(Hilbert-VMD)的特征提取方法，并提出一种双阈值筛选法来确定VMD算法中的分解模态数。首先，根据PD信号功率谱，采用双阈值筛选法确定VMD算法中的分解模态数；其次，采用VMD算法对PD信号进行分解，得到数个有限带宽的固有模态分量(BLIMFs)；然后，对各模态分量进行Hilbert变换并线性叠加后得到PD信号的Hilbert时频谱，并计算各模态分量的边际谱；最后，根据各模态分量的边际谱提取PD信号频域内的特征量，并用支持向量机(SVM)对所提取的特征量进行分类。实验结果表明，对试验环境下和现场实测两种环境下的PD信号，采用该文方法提取得到的特征量均具有较高的正确识别率，充分说明该特征提取方法可以有效提取PD信号特征。对于噪声较大的实测信号，采用该方法得到的正确识别率并未明显降低，说明该方法具有较好的噪声鲁棒性。此外，该文所提Hilbert-VMD方法也为PD信号提供了一种新的时频分析方法。

局部放电 变分模态分解 Hilbert变换 双阈值筛选法 特征提取

0 引言

电力变压器是电力系统中重要的设备之一，其运行状态直接关系到整个电力系统的安全运行[1]。变压器在生产、安装及长期运行过程中不可避免地出现各种绝缘缺陷，这些缺陷将导致不同程度的局部电场畸变，从而诱发局部放电(Partial Discharge，PD)[2]。PD是变压器绝缘劣化的重要征兆和表现形式，有效识别PD信号可以作为目前常用的电气定位[3]和超声定位[4]的辅助手段，弥补上述两种方法定位准确度较低的不足，对及时发现变压器绝缘缺陷和实现PD定位有重要意义。

特征提取是PD信号模式识别过程中的关键步骤之一，提取的特征量能否表征PD信号的本质特征直接关系到模式识别的准确性。目前PD信号特征提取方法主要有基于相位分布模式局部放电(Phase Resolved Partial Discharge，PRPD)统计谱图的特征提取方法和时域分析法两类。PRPD提取方法一般是针对PD信号的统计分布谱图，常用方法有基于φ-n和φ-q二维谱图的统计特征分析法[5]、分形特征分析法[6]、基于散点图的分形特征[7]等。时域分析法是针对高速采集的一次放电产生的时域脉冲所得到的波形特征或可以表征波形时域特征的变换结果，如基于交叉小波变换和相关系数矩阵的特征提取方法[8]、脉冲波形特征提取[9]等。两类特征提取方法都可从不同角度表征PD信号的特征，但同时也存在一些不足。PRPD方法得到的特征量维数较高，会出现信息冗余，导致模式识别效率低，并且该方法需要的样本量较大，无法实现数量规模较小的样本的分析，而运行中的变压器发生故障的几率很低，不同类型PD的有效样本十分有限，因而PRPD方法具有一定的局限性。时域分析方法中基于小波特征提取方法存在小波基选取和分解层数确定的困难，并且无法实现完全自适应分解。脉冲波形特征提取法对放电波形要求较高，若采用含较大噪声或发生畸变的波形数据会直接影响模式识别的准确率。

Hilbert-Huang变换由经验模态分解(Empirical Mode Decomposition，EMD)和Hilbert变换两部分组成，是一种非平稳、非线性的自适应时频分析方法，可根据信号的局部时变特征进行自适应的时频分解[10-12]。目前，该方法已被成功应用于机械和电力系统等领域的信号处理。文献[13]将Hilbert-Huang变换应用于振动故障信号分析，不仅能直观检测信号中的微弱奇异成分，而且可以有效地进行故障诊断，实现早期故障预报。文献[14]应用Hilbert-Huang变换从时域和频域两方面同时对电力系统故障信号进行分析，实现对故障时刻的准确检测。Hilbert-Huang变换是基于EMD算法的，而EMD在递归分解过程中存在模态混叠、无法正确分离频率相近的分量、受采样率影响等缺点[15]，因而EMD得到的模态分量并不能保证有很好的物理意义，各模态分量进行Hilbert变换得到的Hilbert谱，其故障特征不明显，诊断准确度低[16]。

变分模态分解(Variational Mode Decomposition，VMD)算法是K.Dragomiretskiy等于2014年提出的一种非递归的自适应信号处理方法[17]，该方法是在变分问题框架中，利用交替方向乘子法(Alternate Direction Method of Multipliers，ADMM)迭代搜索变分模型最优解，实现每个模态的估计带宽之和最小，并且各模态分量均分别紧紧围绕在对应的中心频率附近。由于该方法本质是维纳滤波，因此具有很好的噪声鲁棒性[15,17-19]。VMD算法解决了EMD算法中因包络误差造成的模态混叠以及易受噪声干扰等问题[17,19]。

采用VMD算法进行信号处理前，需预先设定模态分量的个数K，其设置是否合理直接影响最终的分解结果。若预设K值小于被处理信号中有用成分的个数，会造成分解不充分，致使一些有限带宽的固有模态分量(Band-Limited Intrinsic Mode Functions, BLIMFs)不能被分解出来；若预设K值大于被处理信号中有用成分的个数，则会造成过分解，产生一些无用的虚假分量，干扰原信号中有用成分的分析。因此，K值的确定在VMD算法中占有至关重要的地位。由于VMD算法研究刚刚起步，目前关于确定模态数K的方法还很少。文献[15]通过观察VMD后各模态的中心频率是否相近来判断是否欠分解或过分解，进而择优选取K值,但该方法没有明确的衡量标准，存在很强的主观性，且不能直接通过程序自动确定，需要对被分析信号进行多次VMD，工作量较大。文献[18]提出采用粒子群优化算法来确定K值，虽然可以通过程序自动确定K值，但该方法计算量很大，且优化结果敏感，依赖于算法中参数的设置。由于经VMD算法分解得到的模态分量均紧紧围绕对应的中心频率，且具有窄带特性[17]，因此，可根据被分析信号的频域特点来确定模态数K。

根据VMD算法的特点，本文提出一种基于信号功率谱确定模态数K的方法，即双阈值筛选法。该方法的基本思想是将信号功率谱横坐标(被分析信号的整体频率)分为若干个有限频带，然后根据各频带内频率幅值来判断该频带是否为有效频带，最后统计有效频带的个数，即为VMD模态分量数K。为了解决Hilbert-Huang变换中EMD算法存在的不足，本文提出一种基于VMD和Hilbert变换(Hilbert-VMD)的PD信号分析方法，将其用于PD信号的特征提取。此外，提出一种双阈值筛选法来确定VMD算法中模态数K。首先，根据PD信号功率谱采用双阈值筛选法确定VMD算法的模态数K；其次，对PD信号进行VMD分解，得到若干个模态分量；然后，对各模态分量进行Hilbert变换并线性叠加得到原信号的Hilbert时频谱，计算各模态分量的边际谱；最后，根据各模态分量的边际谱提取PD信号频域内的特征量。为验证本文特征提取方法的有效性，对实验环境下和现场实测PD信号分别采用Hilbert-VMD和Hilbert-Huang两种方法进行特征提取，并采用支持向量机(Support Vector Machine，SVM)对所提取的样本特征量进行模式识别。实验结果表明，对于实验和现场环境的PD信号，本文方法均具有较高的正确识别率，充分验证了该方法能够有效提取PD信号的特征量。此外，Hilbert-VMD方法也为PD信号提供了一种新的时频分析方法。

1 基于改进VMD算法和Hilbert变换的时频分析方法

1.1 VMD算法的基本原理

VMD是一种自适应、准正交、完全非递归的分解方法，可将由多成分组成的信号分解成数个有限带宽的固有模态，并且这些模态绝大部分紧紧围绕在其对应的中心频率周围，均满足文献[20]提出的固有模态(Intrinsic Mode Functions,IMFs)的定义。

与EMD算法所使用的循环筛分剥离不同，VMD算法将信号分解过程转移到变分框架内，通过搜索约束变分模型最优解来实现信号的自适应分解。迭代求解变分模型，最终可以根据被分解信号的频域特性完成信号频带的自适应分解，得到若干个BLIMFs分量，其中每个BLIMF的估计带宽之和最小，各BLIMFs之和等于被分解信号[17]。对于原始信号f，其对应的约束变分模型表达式为

(1)

式中，{uk}为分解得到的K个模态分量，{uk}={u1,…,uK}；{ωk}为各模态分量的中心频率，{ωk}={ω1, …,ωK}。

引入增广Lagrange函数求解上述约束变分问题的最优解，即

L({uk},{ωk},{λ})=

(2)

式中，α为二次惩罚因子，可在高斯噪声存在的情况下保证信号的重构准确度；λ为Lagrange算子，用来保持约束条件的严格性。

利用ADMM求取上述增广Lagrange函数的鞍点，即式(1)约束变分模型的最优解。求得的模态分量uk及中心频率ωk分别为

(3)

(4)

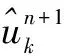
1.2 基于双阈值筛选法的VMD算法分解模态数K的确定

模态数K的确定在VMD算法中具有至关重要的地位。本文提出一种双阈值筛选法，对原始VMD算法中K值确定环节进行改进。

1.2.1 双阈值筛选法的基本原理

由1.1节可知，VMD算法实现过程中模态分量uk和相应中心频率ωk均是在频域内通过求解二次优化问题实现的。对于每个模态分量uk需要通过Hilbert变换计算与之相关的解析信号，通过加入指数项调整各自估计的中心频率，把模态的频谱变换到基带上，带宽通过对解调信号进行H1高斯平滑估计。计算得到的每个模态分量均是紧紧围绕在相应中心频率的，并且具有窄带特性[17]。

功率谱表示信号功率随频率的变化关系[21]，通过功率谱中纵轴峰值可以判断相应频率成分能量的大小。

设信号f(t)的FFT变换为F(ω)，则

(5)

其功率谱为

(6)

PD信号具有较强的随机性，其功率谱分散性较强。图1为某次电晕放电的功率谱。

图1 电晕放电功率谱Fig.1 Power spectrum of corona discharge

PD信号往往是由多种PD信号叠加的复杂的非平稳信号，并且通常包含多种干扰成分，其中每种PD信号都有相应的频域特性。VMD算法的目标是通过分解得到对应于原信号中不同放电成分的模态分量，且每个模态分量都具有窄带特性。因此，可以将PD信号的整个频段分成若干个具有窄带特性的带宽，根据相应带宽中的频率幅值来判断该频带是否为有效频带，有效频带的个数即为模态数K。

综合VMD分解模态和信号功率谱的特点，本文提出一种基于PD信号功率谱频率间隔阈值(横阈值T1)和幅值阈值(纵阈值T2)的双阈值筛选法来确定PD信号的分解模态数K。双阈值筛选法中横阈值T1用来度量原信号中各放电成分的带宽，根据横阈值T1可将原信号的整个频段分成若干个有限频带，分别对应原信号中可能存在的放电频带。纵阈值T2用来度量信号功率谱中相应频率的幅值，幅值超过纵阈值T2的频率看作原信号中的有用频率成分，加以保留；幅值过小的频率看作原信号中的干扰成分，可忽略不计。

采用双阈值筛选法确定模态数K的具体实现步骤为：

1)根据被分析PD信号的频域特点，选取合理的横阈值T1和纵阈值T2。

2)计算PD信号相应的功率谱。

3)全局搜索PD信号功率谱的局部极大值点，并得到相应的下标序列。

4)根据横阈值T1将步骤3中得到的局部极大值点对应的下标序列划分到相应的频带中，临近的多个极值点视为一个有效频率，且取其中幅值最大的极值点作为该频带内有效频率的幅值。

5)根据纵阈值T2对步骤4中得到的各频带内的有效频率的幅值进行判断。幅值大于纵阈值T2的视为有用的频率成分，相应的频带作为被分析信号的有效频带。

6)统计有效窄带的数量，即为VMD分解的模态数K。

1.2.2 自适应阈值选取方案

双阈值筛选法实现的关键在于阈值T1和T2的确定。若设定统一的阈值，必然不适于不同类型的PD信号。此外，如果对不同PD信号根据经验手动一一确定阈值，势必会增加工作量。因此，如何根据PD信号的特征自适应地选取横阈值T1和纵阈值T2具有重要意义。

1)横阈值T1的确定

由于横阈值T1是用来度量被分析信号中模态分量的带宽，因此可以根据被分析信号的频域特征来确定横阈值。

PD信号的测量方法直接影响其频域特征。常用的PD信号检测方法有脉冲电流法、超高频法和超声法。脉冲电流法采用的传感器为耦合电容如变压器套管末屏或电流传感器，其测量频带一般为脉冲电流信号的低频段部分，通常为数 kHz 至数百kHz[22]。超高频检测又分为超高频窄带检测和超高频超宽频带检测，前者中心频率在500 MHz以上，带宽十几MHz或几十MHz，后者带宽可达几GHz[23]。在变压器中，超声波传感器的谐振频率一般在150 kHz左右[24]，清华大学朱德恒等建议选择超声传感单元的频带为70～180 kHz。综上所述，不同测量方法得到的PD信号的频域特征差异很大。因此，选择横阈值T1时，首先要根据测量方法确定被分析PD信号的有效频带范围。

本文根据PD信号中各成分的窄带特性，将PD信号的整体频段分成若干个具有窄带特性的带宽。划分的窄带带宽fband根据测量方法和放电类型有所不同。本文主要研究基于脉冲电流法采集的PD信号。通过大量研究发现，根据测量频带和PD信号类型，基于脉冲电流法采集的PD信号的划分带宽fband的范围为5～10 kHz。相应的横阈值为T1=fbandm/(fmax-fmin)，其中fmax和fmin分别为被分析PD信号的最大和最小频率，m为PD信号的采样点数。根据不同PD信号的频域特性选取fband。

2)纵阈值T2的确定

由双阈值筛选法原理可知，根据纵阈值T2可以将PD信号功率谱按其纵坐标(即频率幅值)划分为有用频率成分和干扰频率成分两类。由电晕放电功率谱(如图1所示)可以看出，幅值较大的频率成分的纵坐标范围较大且分散，而幅值较小的频率成分则比较集中。本文提出根据Otsu准则[25]确定纵阈值T2，即选取某阈值T2令有用频率成分和干扰频率成分两类数据点间的方差最大，此时两类数据点之间的差异也最大。基于Otsu准则确定纵阈值T2的基本原理如下。

设将PD信号功率谱幅值看作长度为m的离散序列{xi},i=1,2,…,m，xmax、xmin分别为该序列的最大值和最小值。

为了描述方便，引入灰度概念，即对应功率谱中频率幅值的大小。设定灰度等级为L(即频率幅值大小的等级)，令dx=(xmax-xmin)/L。统计幅值落在[(l-1)dx,ldx]范围内的值的数量为nl，其中，l为灰度值，l=1,…,L，nl为灰度值为l时的像素。灰度值l出现的概率为pl=nl/N，其中N为总像素数，N=n1+n2+…+nL。

(7)

(8)

(9)

(10)

(11)

(12)

C0和C1两类的类内方差之和为

P1(k)(μ1(k)-μ)2

(13)

式中，μ为整个序列的灰度均值，计算式为

(14)

则可以确定最优阈值为k*dx，令

(15)

综合式(7)～式(15)，可以得到最优纵阈值，即T2=k*dx。

1.3 基于改进VMD算法的Hilbert变换

PD信号进行VMD分解前，根据1.2节确定分解模态数K。信号x(t)经VMD自适应地分解为K个固有模态分量uk(t)，即

(16)

对每个模态分量uk(t)进行Hilbert变换，得到相应的瞬时频率，最终根据所得瞬时频谱得到各模态分量uk(t)的Hilbert谱[26,27]。对式(16)中的每个模态分量uk(t)进行Hilbert变换，即

(17)

式中，P为柯西主值。这一变换对所有LP类存在。

分别构造各模态分量uk(t)的解析信号，即

zk(t)=uk(t)+jH(uk(t))=αk(t)exp(jφk(t))

(18)

式中，αk(t)为幅值函数；φk(t)为相位函数。

(19)

(20)

各模态分量uk(t)的瞬时频率为

(21)

最终得到被分析信号的Hilbert谱，即以极坐标形式的解析信号的实部，本文省略了残量rn，即

(22)

进一步可以定义被分析信号的边际谱为

(23)

Hilbert谱H(ω,t)精确描述了信号的幅值在整个频率段随时间和频率的变化规律。Hilbert变换得到的瞬时频率不同于Fourier变换的全局频率，信号在任意时刻都有对应的瞬时频率，因此，更能体现信号的局部特征。Hilbert边际谱从统计意义上表征整组数据每个频率点的积累幅值分布，它代表整个信号在时间跨度上的幅值累计效应，每个频率值的存在仅仅意味着很可能存在某一频率成分。

此外，由于VMD算法可解决Hilbert-Huang变换方法中EMD分解存在的模态混叠、相近频率难以区分等不足，因此Hilbert-VMD变换可以更好地分析PD信号各成分的时频特性。

2 仿真PD信号的Hilbert-VMD分析

2.1 仿真PD信号

为了证明本文方法的有效性，构造了单指数衰减振荡函数和双指数衰减振荡函数来模拟PD信号，其信号表达式分别为

s1=A1e-(t-t0)/τsin(2πf1t)

(24)

s2=A2[e-1.3(t-t0)/t-e-2.2(t-t0)/t]sin[2πf2(t-t0)]

(25)

因为PD信号通常具有较高频率，为了模拟放电信号特征，采样频率fs=1 GHz；单指数衰减振荡函数s1的幅值A1=250 mV，衰减振荡频率f1=120 MHz；双指数衰减振荡函数s2的幅值A2=300 mV，衰减振荡频率f2=20 MHz；两种信号均在0.3 μs时刻发生。两种放电信号的波形如图2所示。

图2 信号s1和s2波形Fig.2 Waveforms of s1 and s2

目前文献中的仿真PD信号多为不同PD信号在不同时刻发生[28,29]，本文中两种PD信号在同一时刻(0.3 μs)叠加，这类问题的处理对分解算法有更高的要求，也为实际放电信号(多为不同PD信号叠加)的处理提供了很高的参考价值。为模拟现场PD信号，在仿真信号中加入20 dB的白噪声。

s1和s2叠加后以及染噪后的信号波形如图3所示。由图3可看出，仿真PD信号无法分辨信号中的分量成分，加入噪声后，较小的振荡难以区分。

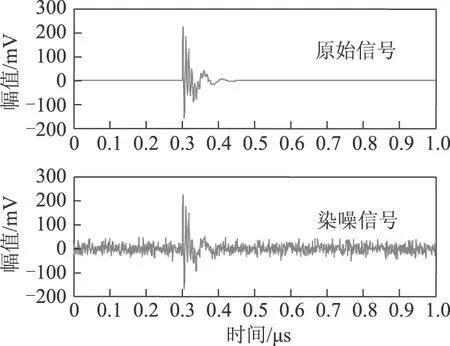
图3 原始信号和染噪信号Fig.3 The original signal and the signal with noise

2.2 仿真PD信号的Hilbert-VMD分析

采用Hilbert-VMD方法对2.1节的仿真PD信号进行分析。PD信号进行VMD前，采用1.2节所述的双阈值筛选法确定模态数K。

图4是染噪信号的功率谱，图中标示的圆圈是通过双阈值筛选法得到的某两个有效频带中最大频率的峰值。据此可以确定该信号中包含两种不同频率的有用成分，分解模态数K=2，与原信号相符，证明双阈值筛选法可以有效确定分解模态数K。

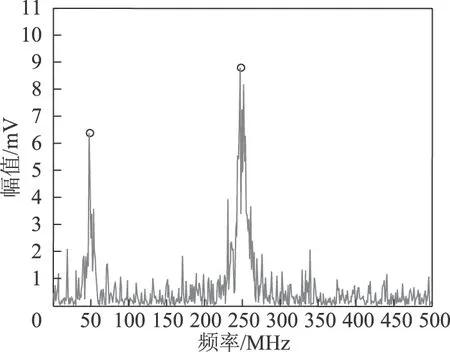
图4 染噪信号功率谱Fig.4 The power spectrum of signal with noise

分解模态数K确定后，进行信号VMD。为了证明VMD算法的优势，本文将VMD结果与EMD结果进行比较。图5为染噪信号分别经VMD和EMD得到的模态分量。由图5a 可知，模态分量u1(t)和u2(t)与图2所示的原信号分量基本一致，充分验证了VMD的有效性。而经EMD自适应分解得到9个IMF模态分量和1个剩余分量，出现了虚假分量，且各IMF与原信号分量差异较大，如图5b所示。由此可知，VMD算法很好地解决了EMD算法存在的模态混叠等不足，更适于复杂PD信号的分解。

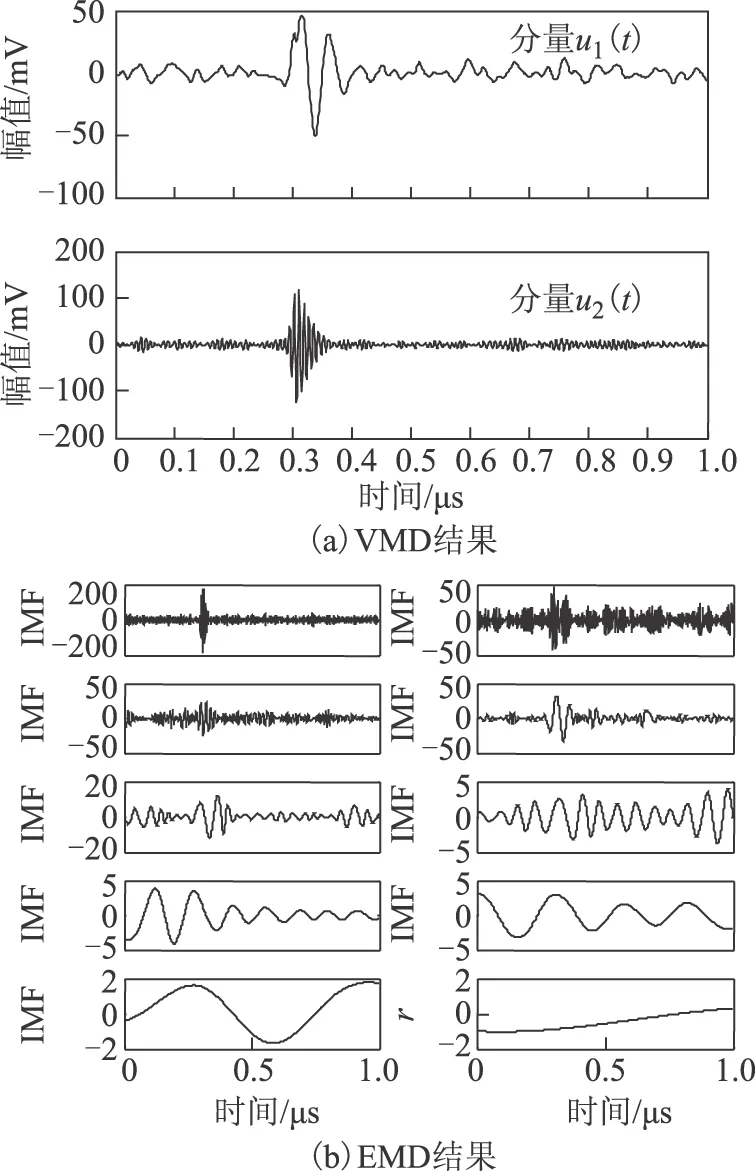
图5 加噪信号VMD和EMD结果Fig.5 The results with noise of VMD and EMD

图6为基于Hilbert-VMD方法得到的Hilbert时频谱和边际谱。Hilbert时频谱中波形颜色对应相应幅值的大小，幅值越大颜色越白。图6a反映了信号的能量随时间和频率的分布情况，图中可明显区分20 MHz和120 MHz两个不同频率分量，其余能量较小的频率成分为信号中的噪声。此外，可以明显看出0.3～0.4 μs 时间段内的频率幅值较大，说明放电脉冲在该时间段出现，与原信号脉冲出现时刻一致。图6b为对应的边际谱，反映了每个频率在整个时间长度内所累积的能量。可以看出，能量主要集中在20 MHz和120 MHz处，其他频段的能量很小，这正好与原信号中s1和s2的频率成分对应。除此之外，Hilbert时频谱和边际谱中噪声成分较少，基本不影响有用成分的分析，这主要是因为VMD算法实质上是多个维纳滤波，具有较好的噪声鲁棒性。综上所述，Hilbert-VMD分析方法具有良好的时频聚集能力，突显信号的局部特征，且具有较好的噪声鲁棒性。

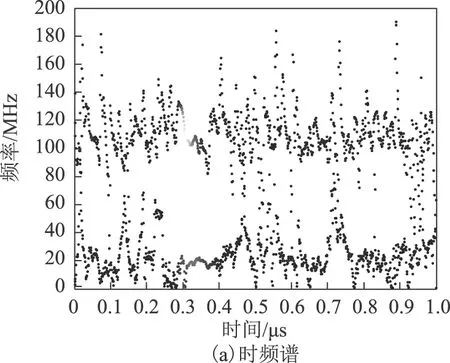
图6 基于Hilbert-VMD得到的Hilbert谱Fig.6 The Hilbert spectrum obtained by Hilbert-VMD

图7为基于Hilbert-Huang方法得到的Hilbert时频谱和边际谱。由图7a可看出，不同频率成分的模态分量很难区分，分布较为散乱，且无法分辨出放电脉冲出现的时刻。这主要是因为EMD过程中存在模态混叠现象，且相近频率的模态无法正确分离。图7b为边际谱，主要存在18 MHz、60.5 MHz、110.5 MHz、150 MHz和229.5 MHz五个主要频率成分。虽然18 MHz 和110.5 MHz两个频率分量在原信号成分s1和s2的频率附近，但有一定的偏移，不能准确表现原信号的频率成分。此外，EMD还产生了原信号频率成分以外的频率分量。与Hilbert-VMD的分析结果相比，Hilbert-Huang变换得到的Hilbert时频谱和边际谱中含有较多干扰成分，说明该方法易受噪声的影响。

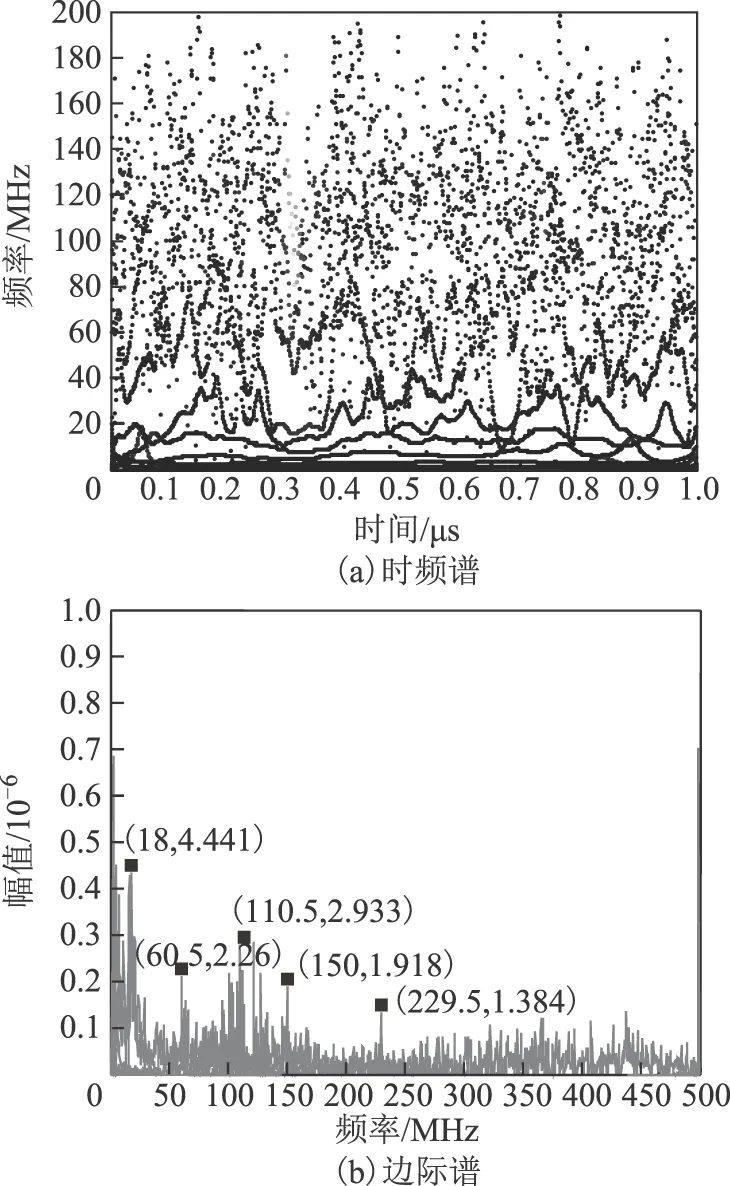
图7 基于Hilbert-Huang得到的Hilbert谱Fig.7 The Hilbert spectrum obtained by Hilbert-Huang

综上所述，基于Hilbert-VMD方法得到的Hilbert时频谱可以区分出不同频率成分的幅值在整个频段上随时间和频率的变化规律，可以较清晰地区分各模态分量，可有效判断出信号中存在的主要频率成分和放电脉冲出现的时刻。通过得到的边际谱可以很容易得到在整个时间长度内积累的能量较大的频率成分。此外，该方法还可有效抑制噪声的影响。

3 试验环境下PD信号分析

3.1 试验环境下PD信号采集

本文试验环境下PD信号取自某公司在线监测系统采集的数据，采集四种不同放电模型的PD信号。放电模型分别为电晕放电、油中多尖对板放电、油中板对板放电和油中悬浮颗粒放电。四种放电模型装置如图8所示。

图8 四种PD实验室模型Fig.8 Four types of partial discharge model

试验中采用IEC60270—2000标准，试验电路为基于脉冲电流法的并联测试电路，采用TWPD-2FPD综合分析仪，其采集频率为20 MHz，带宽为40～300 kHz。高压试验平台型号为TWI 5133-10/100 am。以每个工频周期记录到的放电数据作为一个样本。

3.2 试验环境下PD信号的Hilbert-VMD分析

本文分别采集电晕放电模型、多尖对板放电模型、板对板放电模型和悬浮放电模型四种PD信号共80个样本(每种PD信号选取20个样本)。由于每种放电模型不同，放电的起始电压也不同，因此各放电类型的试验电压并没有可比性，在后续处理中需对PD信号进行归一化。PD信号采样频率很高，每个样本点的数量很大(大于40万个点)，在后续处理过程中会造成计算机死机等严重影响，因此，本文在对信号进行处理前进行了重采样，降低了样本数据量，减少了的计算量。

分别采用Hilbert-VMD方法和Hilbert-Huang方法对上述采集到的PD信号进行分析。

进行VMD前，首先计算PD信号的功率谱，并用双阈值筛选法分别确定四种PD信号的分解模态数。图9为四种PD信号的功率谱以及大致确定的信号主要频率成分(图中圆圈标示)，据此可以得到每种PD信号的VMD的模态数K。

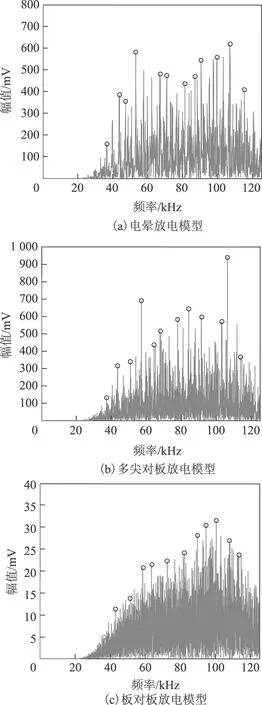
图9 基于双阈值筛选法确定PD信号的分解模态数Fig.9 The number of BLIMFs obtained by double threshold method

图10～图13分别是四种PD信号经Hilbert-VMD变换得到的Hilbert时频谱和边际谱。图14～图17分别是四种PD信号经Hilbert-Huang变换得到的Hilbert时频谱和边际谱。分别比较采用两种方法得到的变换结果。

四种PD信号采用Hilbert-VMD变换得到的Hilbert时频谱中信号的主要频率成分基本可以区分开，且可以根据波形颜色深浅明显看出放电脉冲出现的时刻。对应的边际谱图中可以清晰地区分出各模态对应的频率成分，基本不受噪声的干扰。

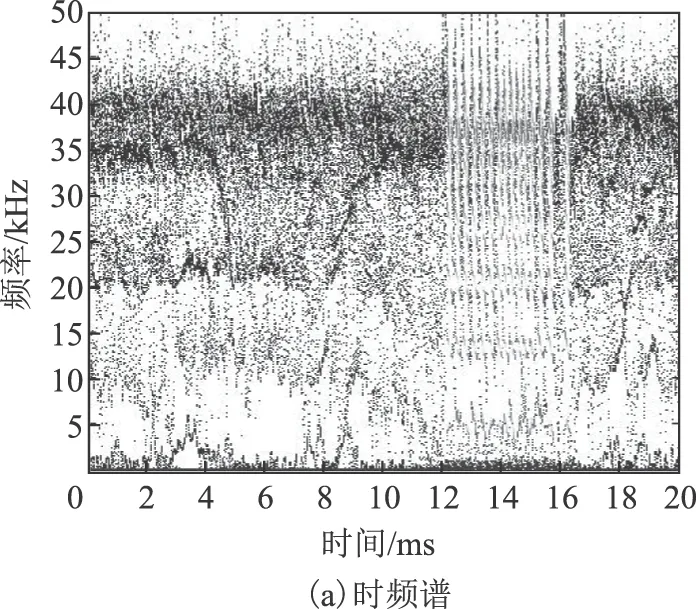
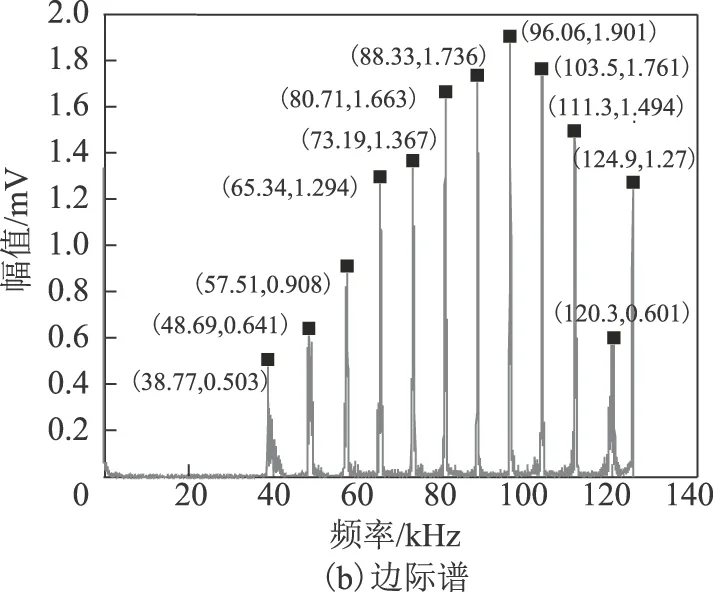
图10 基于Hilbert-VMD的电晕放电的分析结果Fig.10 The results of corona discharge based on Hilbert-VMD

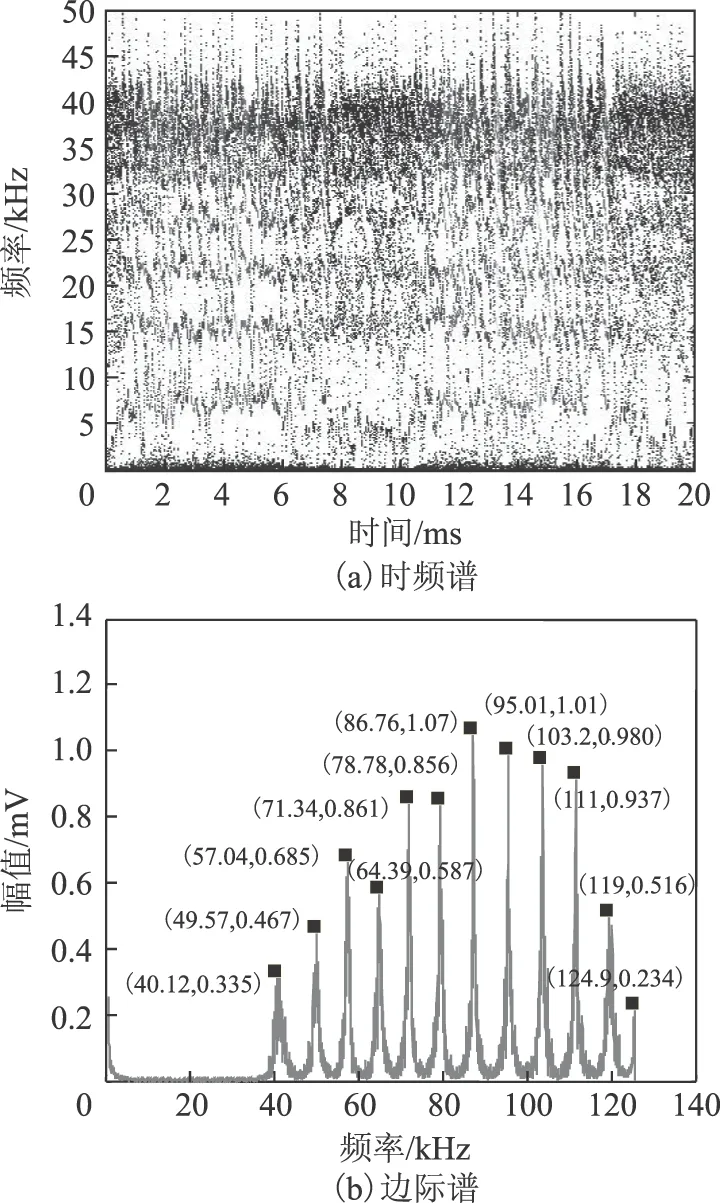
图11 基于Hilbert-VMD的多尖对板放电的分析结果Fig.11 The results of needle-matrix-to-plate discharge based on Hilbert-VMD

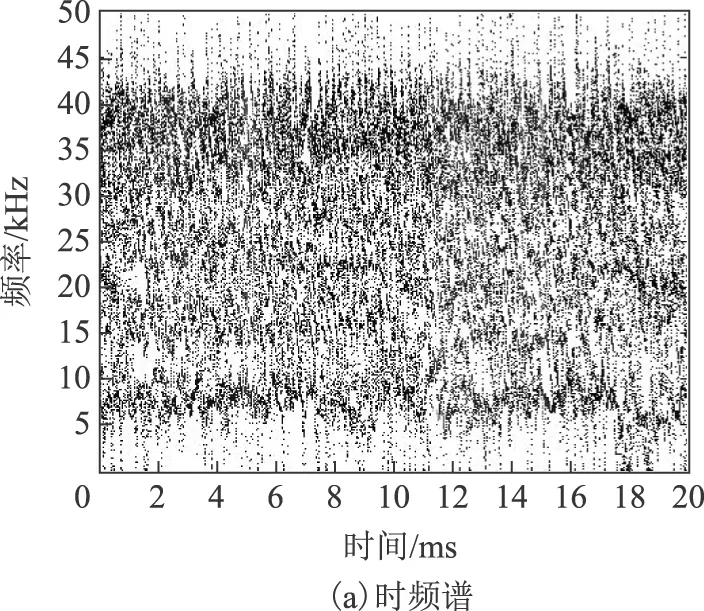
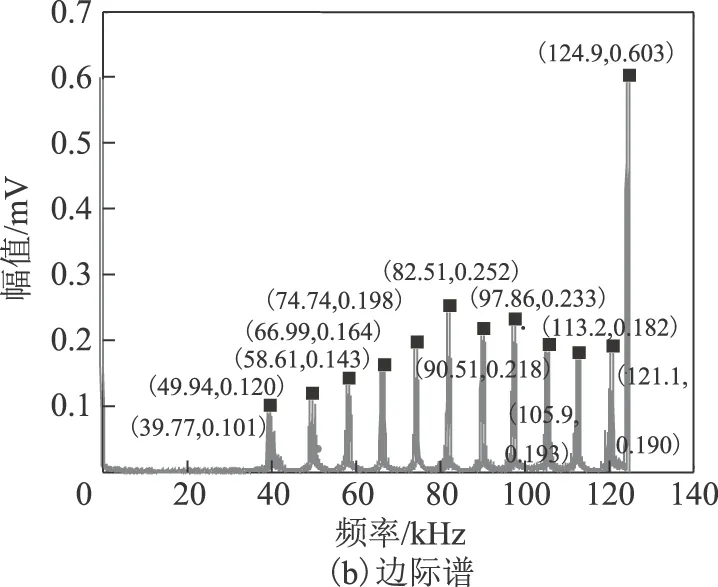
图12 基于Hilbert-VMD的板对板放电的分析结果Fig.12 The results of plate-to-plate dischargebased on Hilbert-VMD

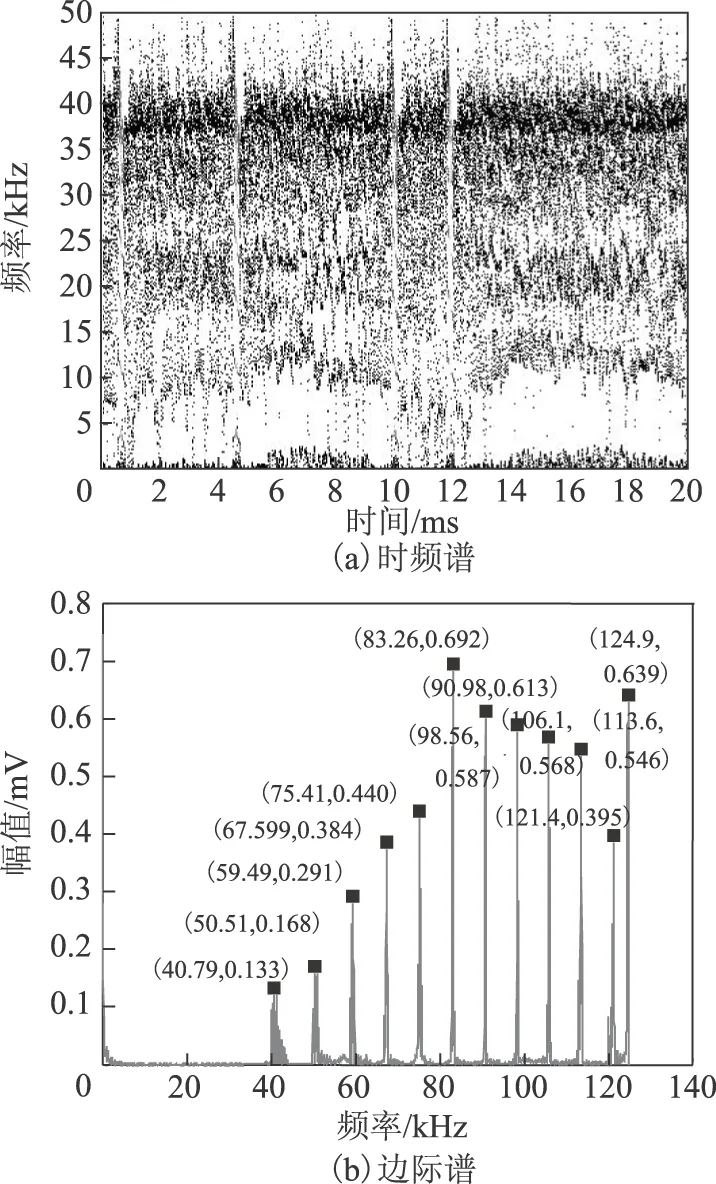
图13 基于Hilbert-VMD的悬浮放电的分析结果Fig.13 The results of suspended discharge based on Hilbert-VMD

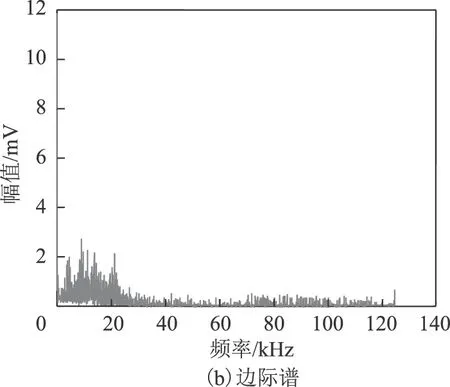
图14 基于Hilbert-Huang的电晕放电的分析结果Fig.14 The results of corona discharge based on Hilbert-Huang

图15 基于Hilbert-Huang的多尖对板放电的分析结果Fig.15 The results of needle-matrix-to-plate discharge based on Hilbert-Huang

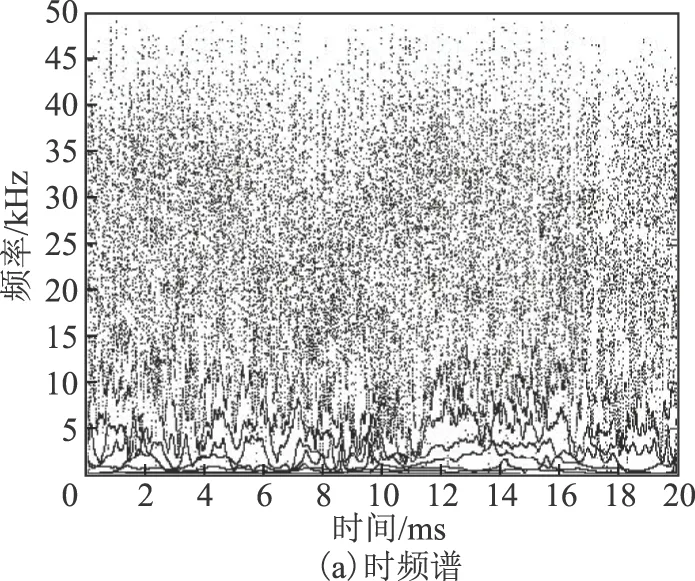
图16 基于Hilbert-Huang的板对板放电的分析结果Fig.16 The results of plate-to-plate discharge based on Hilbert-Huang

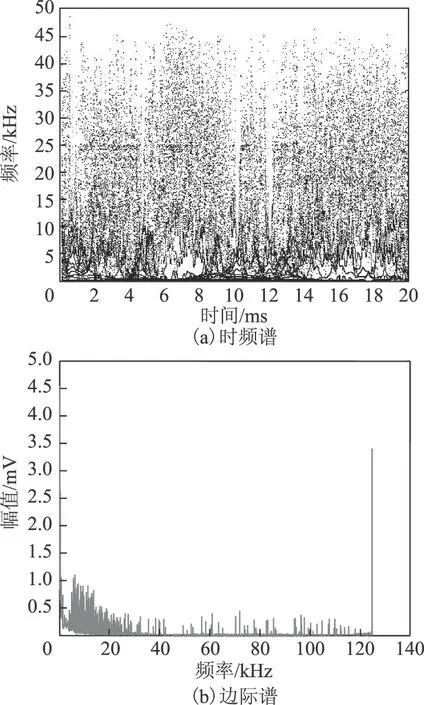
图17 基于Hilbert-Huang的悬浮放电的分析结果Fig.17 The results of suspended discharge based on Hilbert-Huang

采用Hilbert-Huang变换得到的Hilbert时频谱中，各成分之间存在相互混叠，分布较散乱，无法区分信号中各频率成分，且放电脉冲出现的时刻不明显。对应的边际谱中虽然会出现几个幅值较大的频率成分，但是大部分频率之间很紧密，无法清晰分辨出信号中的主要频率成分。此外，Hilbert时频谱和边际谱中存在较多的噪声成分，不利于原信号主要频率成分的分析。

综上所述，Hilbert-VMD方法可以有效表征PD信号幅值在整个频段上随时间和频率的变化规律，区分PD信号中的主要频率成分，并且可以有效抑制噪声的干扰。Hilbert-VMD方法同时也为PD信号提供了一种新的时频分析方法。

3.3 基于Hilbert-VMD方法的PD信号特征提取

由四种PD信号的边际谱可以看出，无论采用Hilbert-VMD方法还是Hilbert-Huang方法，每种PD信号对应的边际谱均不同于其他类型，因此可将其作为区分放电类型的特征。为了突显PD信号中各主要频率成分(即各模态分量)的频域特性，分别提取各模态分量边际谱的频域特征[30]作为PD信号的特征量。Fme、Fσ、Fban分别为频域内频谱均值、方差和带宽，Fmax为最高幅值对应的频率。每个PD信号样本对应的特征量为

Pi={Fme1,Fσ1,Fban1,Fmax1,…,FmeK,FσK,FbanK,FmaxK}

(26)

式中，Pi为第i个信号的特征量的集合。

基于Hilbert-VMD变换的PD信号特征提取过程如图18所示。首先，采用双阈值筛选法确定被分析PD信号的模态数K；然后，对PD信号进行VMD，得到K个模态分量；将各模态分量分别进行Hilbert变换，并提取各模态分量边际谱的频域特征量；最后，将各模态分量的频域特征量进行组合得到原PD信号的特征量。

图18 基于Hilbert-VMD的特征提取过程Fig.18 Feature extraction process based on Hilbert-VMD

由于PD信号比较复杂，经分解得到的模态分量比较多，且每个模态均得到四个特征量，最终得到的特征量维数很大。这在后续模式识别过程中造成维数灾难，并且可能因特征量的冗余而影响模式识别结果。因此，本文对得到的特征量采用主成分分析(Principal Component Analysis,PCA)进行降维处理。经验证，不同PD信号的前10个特征值的贡献率为90%以上，因此，进行PCA降维时，特征量的维数选为10。

分别采用Hilbert-VMD和Hilbert-Huang两种方法提取四种PD信号的频域特征量。图19是分别基于Hilbert-VMD和Hilbert-Huang方法提取的频域特征量的Fisher聚类效果,其中Y1和Y2是频域特征量降维到二维空间作图后的两个坐标。比较图19a、图19b可看出，基于Hilbert-VMD方法提取的四种PD信号的频域特征量已经完全区分开，并且取得了较好的聚类性能；而基于Hilbert-Huang方法提取的四种PD信号的频域特征量不能区分，聚类性能差。由此可以说明，基于Hilbert-VMD方法提取的特征量可以有效表征不同PD信号的特征。

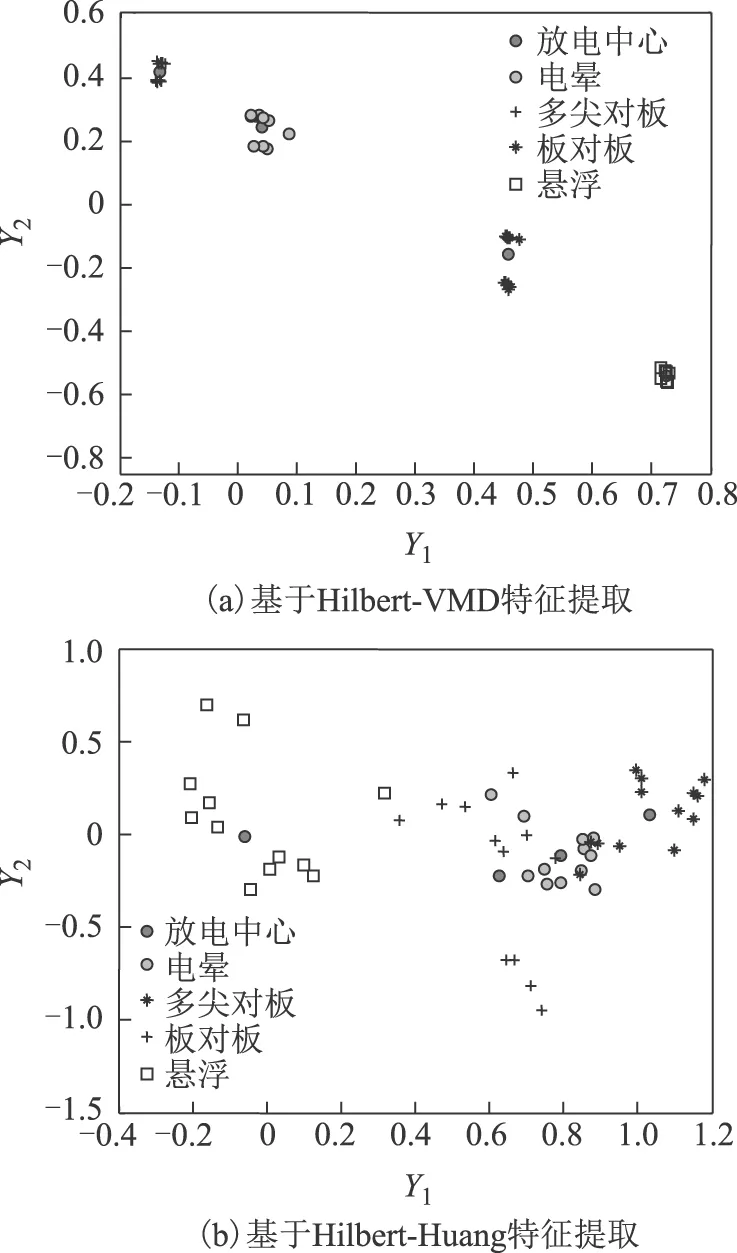
图19 基于Hilbert-VMD和Hilbert-Huang提取的频域特征量的Fisher聚类Fig.19 Fisher features extraction effect of Hilbert-VMD and Hilbert-Huang

3.4 基于支持向量机的PD信号模式识别

选取四种PD信号共80个样本(每种放电类型各20个样本)。从所有样本中随机抽取50组数据用于SVM网络训练，剩余30组数据用于测试。分别将基于Hilbert-VMD和Hilbert-Huang两种方法得到的频域特征量输入SVM进行训练和测试。由于分类过程中，每次分类前训练样本和测试样本都是随机抽取的，每次试验的识别结果有一定的差异，因此，本文对每种情况分别进行50次试验，将50次试验得到的平均值作为最终结果，见表1。

由表1可看出，基于Hilbert-VMD方法提取的特征量的正确识别率远高于基于Hilbert-Huang方法提取的特征量。这是因为Hilbert-Huang方法中的EMD是一种递归模式的分解方法，在分解过程中将包络线估计误差不断传播，且其分解过程中与故障相关的信号频带中心和带宽是不确定的，无法抑制信号中存在的噪声和间歇信号，分解结果中存在虚假分量和模态混叠，这些都使各模态边际谱无法正确表征信号故障特征，最终导致基于Hilbert-Huang方法提取的特征量的正确识别率较低。而VMD是一种非递归的分解模式，通过迭代搜索变分模型最优解来确定每个模态分量的中心频率和频带，可以自适应地实现信号的频域剖分和各分量的有效分离，分解得到的模态分量大部分都紧紧围绕在中心频率周围，可以很好地反映PD信号的局部特征。并且VMD具有维纳滤波特性，具有较好的噪声鲁棒性。因此，基于Hilbert-VMD方法提取的特征量的正确识别率较高。

表1 两种特征提取方法识别效果对比

4 现场实测PD信号分析

为了验证本文提出的基于Hilbert-VMD特征提取方法对含较强噪声的现场实测PD信号的适用性，采用两种不同的现场实测PD信号对该方法进行验证。两组现场实测数据分别为江苏南京某电厂和广东某核电站测得的PD信号，检测方法均为脉冲电流法，两种情况分别采集50组和40组样本。PD信号的特征提取过程与3.3节类似，在此不再赘述。

在实测PD信号样本集(共90个)中随机抽取50组数据用于训练SVM网络，剩余40组数据作为测试数据。表2为两组实测PD信号分别以基于Hilbert-VMD和Hilbert-Huang两种方法提取的特征量经SVM得到的识别结果。为了使结果更具一般性，每种情况进行50次试验，将试验平均值作为最终结果。

表2 两种特征提取方法识别效果对比

由表2可知，基于Hilbert-VMD方法提取的特征量仍具有较高的正确识别率，并且高于基于Hilbert-Huang方法提取的特征向量的正确识别率。充分说明了Hilbert-VMD方法同样适用于含噪声较强的现场实测PD信号的特征提取，具有较强的噪声鲁棒性。

5 结论

1)提出一种基于VMD算法和Hilbert变换的特征提取方法。变压器PD信号经VMD算法得到若干模态分量，对各模态分量分别进行Hilbert变换并线性叠加得到原信号的Hilbert时频谱，计算各模态分量的边际谱，提取各模态分量边际谱的频域特征量作为PD信号的特征量。

2)提出一种双阈值筛选法来确定VMD算法的模态分解数，并给出了阈值的确定方法，为VMD算法中模态数K的确定提供了一种可行的方案。

3)用基于Hilbert-VMD的方法提取不同类型的PD信号的特征量，并用SVM分类器进行放电类型识别。将识别结果与基于Hilbert-Huang方法提取的特征量的识别结果进行比较，结果表明，基于Hilbert-VMD的特征提取方法对各类PD信号的正确识别率较高，具有很好的识别效果。

[1] 尹金良, 朱永利, 俞国勤. 基于多分类相关向量机的变压器故障诊断新方法[J]. 电力系统保护与控制, 2013, 41(5): 77-82. Yin Jinliang, Zhu Yongli, Yu Guoqin. New transformer fault diagnosis method based on multi-class relevance vector machine[J]. Power System Protection and Control, 2013, 41(5): 77-82.

[2] 唐炬, 董玉林, 樊雷, 等. 基于Hankel矩阵的复小波-奇异值分解法提取局部放电特征信息[J]. 中国电机工程学报, 2015, 35(7): 1808-1817. Tang Ju, Dong Yulin, Fan Lei, et al. Feature information extraction of partial discharge signal with complex wavelet transform and singular value decomposition based on Hankel matrix[J]. Proceedings of the CSEE, 2015, 35(7): 1808-1817.

[3] Fuhr J, Haessig M， Boss P, et al. Detection and location of internal defects in the insulation of power transformers[J]. IEEE Transactions on Electrical Insulation, 1993, 28(6): 1057-1067.

[4] Bozzo R，Guastavino F. PD detection and localization by means of acoustic measurements on hydogenerator stator bars[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1995, 2(4): 660-666.

[5] 温敏敏, 宋建成, 宋渊, 等. 基于局部放电统计特征参量分析的矿用干式变压器绝缘状态评估[J]. 高电压技术, 2014, 40(8): 2398-2405. Wen Minmin, Song Jiancheng, Song Yuan, et al. Insulationcondition estimation of mining flameproof dry-type transformer based on statistical characteristic parameters analysis of partial discharge[J]. High Voltage Engineering, 2014, 40(8): 2398-2405.

[6] 李剑, 孙才新, 杜林, 等. 局部放电灰度图象分维数的研究[J]. 中国电机工程学报, 2002, 22(8): 123-127. Li Jian, Sun Caixin, Du Lin, et al. Study on fractal dimension of PD gray intensity image[J]. Proceedings of the CSEE, 2002, 22(8): 123-127.

[7] 高凯, 谈克雄, 李福祺, 等. 基于散点集分形特征的局部放电模式识别研究[J]. 中国电机工程学报, 2002, 22(5): 23-27. Gao Kai, Tan Kexiong, Li Fuqi, et al. Pattern recognition of partial discharges based on fractal features of the scatter set[J]. Proceedings of the CSEE, 2002, 22(5): 23-27.

[8] 尚海昆, 苑津莎, 王瑜, 等. 基于交叉小波变换和相关系数矩阵的局部放电特征提取[J]. 电工技术学报, 2014, 29(4): 274-281. Shang Haikun, Yuan Jinsha, Wang Yu, et al. Feature extraction for partial discharge based on cross-wavelet transform and correlation coefficient matrix[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 274-281.

[9] 鲍永胜. 局部放电脉冲波形特征提取及分类技术[J]. 中国电机工程学报, 2013, 33(28): 168-175. Bao Yongsheng. Partial discharge pulse waveform feature extraction and classification techniques[J]. Proceedings of the CSEE, 2013, 33(28): 168-175.

[10]刘志刚, 李文帆, 孙婉璐. Hilbert-Huang变换及其在电力系统中的应用[J]. 电力自动化设备, 2012, 32(4): 109-116. Liu Zhigang, Li Wenfan, Sun Wanlu. Hilbert-Huang transform and its applications in power system[J]. Electric Power Automation Equipment, 2012, 32(4): 109-116.

[11]缪希仁, 吴晓梅, 石敦义, 等. 采用HHT振动分析的低压断路器合闸同期辨识[J]. 电工技术学报, 2014, 29(11): 154-161. Mou Xiren, Wu Xiaomei, Shi Dunyi, et al. Switching synchronism identification of low voltage circuit breaker utilizing HHT analysis to vibration signal[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 154-161.

[12]刘毅力, 陶学军, 李佳, 等. 基于HHT的风力发电机组滚动轴承故障特征提取[J]. 电力系统保护与控制, 2012, 40(20): 79-82. Liu Yili, Tao Xuejun, Li Jia, et al. Feature extraction of rolling bearing for wind generator based on HHT[J]. Power System Protection and Control, 2012, 40(20): 79-82.

[13]向玲, 朱永利, 唐贵基. HHT方法在转子振动故障诊断中的应用[J]. 中国电机工程学报, 2007, 27(35): 84-89. Xiang Ling, Zhu Yongli, Tang Guiji. Application of Hilbert-Huang transform method in vibration faults diagnosis for rotor system[J]. Proceedings of the CSEE, 2007, 27(35): 84-89.

[14]李天云, 赵妍, 季小慧, 等. HHT方法在电力系统故障信号分析中的应用[J]. 电工技术学报, 2005, 20(6): 87-91. Li Tianyun, Zhao Yan, Ji Xiaohui, et al. Application of HHT method for analysis of fault signal in electric power system[J]. Transactions of China Electrotechnical Society, 2005, 20(6): 87-91.

[15]刘长良, 武英杰, 甄成刚. 基于变分模态分解和模糊 C 均值聚类的滚动轴承故障诊断[J]. 中国电机工程学报, 2015, 35(13): 1-8. Liu Changliang, Wu Yingjie, Zhen Chenggang. Rollingbearing fault diagnosis based on variational mode decomposition and fuzzy C means clustering[J]. Proceedings of the CSEE, 2015, 35(13): 1-8.

[16]雷亚国. 基于改进Hilbert-Huang变换的机械故障诊断[J]. 机械工程学报, 2011, 47(5): 71-77. Lei Yaguo. Machinery fault diagnosis based on improved Hilbert-Huang transform[J]. Journal of Mechanical Engineering, 2011, 47(5): 71-77.

[17]Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.

[18]唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报, 2015, 49(5): 73-81. Tang Guiji, Wang Xiaolong. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing[J]. Journal of Xi′an Jiaotong University, 2015, 49(5): 73-81.

[19]高艳丰, 朱永利, 闫红艳, 等. 基于VMD和TEO的高压输电线路雷击故障测距研究[J]. 电工技术学报, 2016, 31(1): 24-33. Gao Yanfeng, Zhu Yongli, Yan Hongyan, et al. Study on lighting fault locating of high-voltage transmission lines based on VMD and TEO[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 24-33.

[20]Daubechies I, Lu Jianfeng, Wu H T. Synchrosqueezed wavelet transforms: an empirical mode decomposition-like tool[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 243-261.

[21]郑君里, 应启珩, 杨为理. 信号与系统[M]. 第二版. 北京: 高等教育出版社, 2000.

[22]周玉钏. 变压器局部放电诊断方法研究[J]. 电气开关, 2012 (2): 47-49. Zhou Yuchuan. Study on diagnostic method of partial discharge of transformers[J]. Electric Switcher, 2012 (2): 47-49.

[23]郭俊, 吴广宁, 张血琴, 等. 局部放电检测技术的现状和发展[J]. 电工技术学报, 2005, 20(2): 29-35. Guo Jun, Wu Guangning, Zhang Xueqin, et al. The actuality and perspective of partial discharge detection techniques[J]. Transactions of China Electrotechnical Society, 2005, 20(2): 29-35.

[24]李军浩, 韩旭涛, 刘泽辉, 等. 电气设备局部放电检测技术述评[J]. 高电压技术, 2015, 41(8): 2583-2601. Li Junhao, Han Xutao, Liu Zehui, et al. Review on partial discharge measurement technology of electrical equipment[J]. High Voltage Engineering, 2015, 41(8): 2583-2601.

[25]许向阳, 宋恩民, 金良海. Otsu准则的阈值性质分析[J]. 电子学报, 2009, 37(12): 2716-2719. Xu Xiangyang, Song Enmin, Jin Lianghai. Characteristic analysis of threshold based on Otsu criterion[J]. Acta Electronica Sinica, 2009, 37(12): 2716-2719.

[26]Yang J N, Lei Ying, Pan Shuwen, et al. System identification of linear structures based on Hilbert-Huang spectral analysis, part 1: normal modes[J]. Earthquake Engineering & Structural Dynamics, 2003, 32(9): 1443-1467.

[27]Yang J N, Lei Ying, Pan Shuwen, et al. System identification of linear structures based on Hilbert-Huang spectral analysis, part 2: complex modes[J]. Earthquake Engineering & Structural Dynamics, 2003, 32(10): 1533-1554.

[28]李天云, 高磊, 聂永辉, 等. 基于经验模式分解处理局部放电数据的自适应直接阈值算法[J]. 中国电机工程学报, 2006, 26(15): 29-34. Li Tianyun, Gao Lei, Nie Yonghui, et al. A new adaptive direct-threshold algorithm to partial discharge data processing based on empirical mode decomposition[J]. Proceedings of the CSEE, 2006, 26(15): 29-34.

[29]袁娜, 朱永利, 梁涵卿. 结合矩形窗的EEMD局部放电信号去噪[J]. 电力系统及其自动化学报, 2015, 27(3): 54-58. Yuan Na, Zhu Yongli, Liang Hanqing. EEMD de-noising method using rectangular window[J]. Proceedings of the CSU-EPSA, 2015, 27(3): 54-58.

[30]尚海昆, 苑津莎, 王瑜, 等. 多核多分类相关向量机在变压器局部放电模式识别中的应用[J]. 电工技术学报, 2014, 29(11): 221-228. Shang Haikun, Yuan Jinsha, Wang Yu, et al. Partial discharge pattern recognition in power transformer based on multi-kernel multi-class relevance vector machine[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 221-228.

(编辑 张洪霞)

Feature Extraction and Classification on Partial Discharge Signals of Power Transformers Based on Improved Variational Mode Decomposition and Hilbert Transform

ZhuYongliJiaYafeiWangLiuwangLiLiZhengYanyan

(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University Baoding 071003 China)

Feature extraction of partial discharge (PD) signals is one of the key step in the analysis of PD signals. Owing to the shortcomings of existing feature extraction methods, a novel method based on the variational mode decomposition (VMD) and Hilbert transform (Hilbert-VMD) was put forward in this paper. Meanwhile, a dual threshold method was proposed to determine the number of decomposition modes. Firstly, the number of decomposition modes was obtained by using the dual threshold method according to power spectra of PD signals. Secondly, the known PD signals were decomposed by VMD and several band-limited intrinsic mode functions(BLIMFs) were extracted. Then each BLIMFs was processed by Hilbert transform and the marginal spectrum of each BLIMFs was calculated. Finally, the features of PD signals in the frequency domain were extracted based on the marginal spectrum of each BLIMFs. In order to verify the effectiveness of the proposed feature extraction method, PD signals in laboratory environment and field measured were processed by Hilbert-VMD and Hilbert-Huang respectively and support vector machine (SVM) classifiers were utilized for pattern recognition. Compared with the feature extraction method based on Hilbert-Huang, the feature extracted by the proposed method have a higher correct recognition rate. The experimental results show that the proposed method can effectively extract the features of PD signals. The correct recognition rate of field measured signals using the proposed method is not significantly reduced and it is proved that the proposed method has better noise robustness. In addition, the Hilbert-VMD also provides a new time-frequency analysis method for PD signals.

Partial discharge, variational mode decomposition, Hilbert transform, dual threshold method, feature extraction

国家自然科学基金(51677072)和中央高校基本科研业务费专项资金(2016XS101)资助项目。

2015-11-11 改稿日期2016-04-11

TM85

朱永利 男，1963年生，教授，博士生导师，研究方向为网络化监控与智能信息处理。

E-mail:yonglipw@163.com(通信作者)

贾亚飞 女，1988年生，博士研究生，研究方向为输变电设备故障诊断。

E-mail: jiayafeiyanshan@163.com