基于广义S变换模时频矩阵的局部放电特高频信号去噪方法
刘宇舜 周文俊 李鹏飞 王 勇 田 妍
(1. 武汉大学电气工程学院 武汉 430072 2. 广州供电局有限公司 广州 510620)
基于广义S变换模时频矩阵的局部放电特高频信号去噪方法
刘宇舜1周文俊1李鹏飞1王 勇2田 妍2
(1. 武汉大学电气工程学院 武汉 430072 2. 广州供电局有限公司 广州 510620)
为有效抑制局部放电特高频信号中的噪声干扰,提出一种基于广义S变换模时频矩阵的去噪方法。基于二维模时频矩阵,采用区域最大能量法提取周期性窄带干扰的特征量,并通过矩阵逆向分离将其去除;采用奇异值分解去噪方法抑制信号中的高斯白噪声。使用该方法对仿真信号和实验室实测信号进行去噪处理,并与传统方法去噪结果进行对比。结果表明,所提方法能有效抑制局部放电信号特高频信号中的噪声,同时更好地保留了原始局部放电信号特征。对现场实测信号进行去噪处理,与传统方法相比,该方法具有较高的噪声抑制比和较低的幅值衰减比,可以有效提取局部放电超高频信号。
局部放电 去噪 广义S变换 窄带干扰 区域最大能量法 高斯白噪声 奇异值分解
0 引言
局部放电(Partial Discharge, PD)是绝缘劣化的主要原因及表现形式,对其进行检测已成为评估电力设备绝缘状态的有效方法[1]。变电站中高压设备出现PD时,伴随产生的特高频(Ultrahigh Frequency, UHF)电磁波信号可通过没有金属屏蔽效果的介质向设备外部辐射,从而可以利用外置UHF天线来检测PD[2]。然而在现场PD检测中,电气设备处于带电运行状态,对检测环境电磁干扰严重。同时使用的UHF天线通常为超宽带天线,易受到空间中各类无线电磁波的干扰,导致较微弱局部放电UHF信号易淹没于严重的背景噪声中,无法进行准确有效地PD检测[3]。因此对接收信号中噪声进行抑制是UHF法检测PD的关键问题。
局部放电UHF法检测中的干扰一般可分为三类:随机脉冲干扰、周期性窄带干扰和高斯白噪声。随机脉冲干扰是由于可控硅等开关器件动作产生的,由于其频率低、幅值高,较易识别与滤除[4]。周期性窄带干扰主要是由系统的高次谐波、载波通信、无线电通信等产生。由于周期性干扰幅值通常高于PD信号,可以将检测到的PD信号完全淹没,尤其当周期性干扰的频率与PD信号的频率出现混合时,无法使用简单的滤波手段抑制干扰[5]。国内外学者对抑制周期性窄带干扰进行了大量研究。文献[6,7]采用快速傅里叶变换方法有效抑制了窄带干扰,但是由于频谱泄露和阈值选取偏差问题,导致计算结果存在误差。文献[8-10]利用小波分解的时频分析能力,有效地减小了计算误差,但由于PD信号的多样性,难以选择完全适合局放脉冲波形的小波基函数。高斯白噪声主要是由电气设备的热噪声引起[4]。当高斯白噪声与周期性窄带干扰混合时,传统的小波变换、经验模态分解等方法无法有效滤除干扰,需在去除周期性窄带干扰后再使用传统方法抑制高斯白噪声干扰,导致计算时间增加及信号失真[11]。
本文采用广义S变换对UHF天线检测到的信号进行时频分析,得到广义S变换的模时频矩阵。采用区域最大能量法在二维模时频矩阵上计算出周期性窄带干扰信号特征量并通过矩阵逆向分离将其去除。不同于现有基于一维时域信号的高斯白噪声抑制方法,本文基于二维模时频矩阵,采用奇异值分解法抑制信号中的高斯白噪声。使用本文方法对仿真与实测PD信号进行去噪处理,并与传统方法去噪结果进行对比,证明了本文去噪方法的准确性和有效性。
1 广义S变换原理
由于PD信号为非平稳信号,单纯用时域或者频域信息无法有效表示PD信号频率随时间变化的局部特征。S变换作为典型的时频分析方法,可以将一维时域信号映射至二维时频域内,反映出局部放电UHF信号频率随时间变换的局部特征[12]。
S变换最早由R.G.Stockwell提出[13],其对信号x(t)的S变换定义为
(1)
式中,f为频率;t、τ为时间;w(t-τ,f)为高斯窗函数,其表达式为
(2)
S变换结合了短时傅里叶变换和连续小波变换的优点,属于可逆的局部时频分析方法。由于引入了高度和宽度随频率变化的高斯窗函数,使其时频分辨率随频率变化,在克服了短时傅里叶变换时频分辨率固定不变的同时,也避免了连续小波变换中的小波函数选择困难的缺点。
由于S变换窗函数的形式是固定的,使其在实际应用中受到限制,因此C.R.Pinnegar通过引入调节因子λ(λ>0)对高斯窗函数进行改进[14],其计算式为
(3)
故信号x(t)的广义S变换定义为
(4)
这种形式的广义S变换实质上是利用λf替代f,从而可通过调节因子λ的作用来控制f的变化速度,当0<λ<1时,高斯窗宽度越宽,频域分辨率越高;当λ>1时,高斯窗宽度越窄,时域分辨率越高。可见λ的引入改变了时频分辨率随频率变化的分布,通过改变参数λ使广义S变换具有更好的适应性和灵活性。
在实际应用计算中,需要对广义S变换进行离散化表示,令f=n/(NT)、τ=iT,其中T为采样时间间隔,N为总采样点数,离散广义S变换定义为
(5)
式中,i,m,n=0,1,…,N-1。
由式(5)对离散序列计算得到的是一个二维时频矩阵,列对应时间采样点,行对应频率采样点。矩阵元素为复数,为简化处理,对该矩阵求模,得到广义S变换的模矩阵(GeneralizedS-transformModularMatrix,GSMM)。GSMM为二维时频矩阵,可通过三维图形绘制出信号时频谱图,反映PD信号的时频特征,包括时间、频率、幅值、能量和相位等,有助于对局部放电UHF信号进一步分析[15]。
2 周期性窄带干扰抑制方法
2.1 仿真信号分析
由于变电站现场实际检测的局部放电UHF信号存在各种噪声干扰,难以获得纯净的PD信号进行研究分析,因而本文采用仿真信号分析局部放电UHF信号及各类背景噪声的去除方法。通过大量现场PD试验和相关文献分析,检测到的局部放电UHF信号多呈现衰减振荡的形式[2-4]。本文选择单指数衰减振荡和双指数衰减振荡数学模型[12]来模拟上述现场局部放电UHF信号,计算式分别为
(6)
(7)
式中,τc为衰减系数;fc为振荡频率;A1、A2为信号幅值。仿真软件为Matlab 2014b,模拟四种PD信号脉冲,各脉冲参数见表1。仿真中信号采样率设置为10 Gs/s。在140 ns时间段内加入以上四种形式的模拟PD脉冲,如图1a所示。

表1 局部放电信号参数

图1 模拟信号Fig.1 Simulated signal
通过叠加不同频率的周期性窄带干扰以模拟现场环境中的混频窄带干扰。周期性窄带干扰主要呈正弦或余弦波状,使用UHF法检测PD时常遇到载波通信信号和手机通信信号干扰,故窄带干扰频率fi设为f1=470 MHz、f2=900 MHz、f3=1 800 MHz[6],周期性窄带干扰信号的数学表达式为
(8)
式中,Ai为各窄带干扰信号幅值,均设为2 mV。由于现场检测时会存在一定的高斯白噪声干扰,故在此基础上叠加分布为(0, 0.42)的高斯白噪声干扰。图1b为最终的染噪局部放电UHF信号,原始的PD信号在时域上已无法识别。
2.2 窄带干扰特征量提取
在局部放电周期性窄带干扰频率特征提取过程中,当干扰信号与PD信号频率相近时,使用传统S变换识别频率特征时会出现严重的频率重叠情况,不利于窄带干扰频率特征的提取[16]。由于广义S变换本质上仍是加窗型傅里叶变换,其时频分辨率仍受Heisenberg测不准原理的制约,时间分辨率和频率分辨率无法同时达到最高精度。经仿真可知,当取λ=0.3时,图1b中染噪局部放电UHF信号的GSMM时间分辨率和频率分辨率可以同时达到所需精度,图2为其基于广义S变换模时频矩阵绘制出的时频分布等高线,即信号的时频谱。

图2 染噪PD信号时频谱Fig.2 Time-frequency spectrum of noisy PD signal
根据染噪PD信号的时频谱可以分析所含噪声的类型,并基于模时频矩阵进行相应的噪声干扰抑制处理。由于周期性窄带干扰持续时间长且频率集中,PD信号频率分布较宽,故两者易于从时频谱中分辨出来。但由于其与PD信号和高斯白噪声频率混叠,无法通过图2直接判断出窄带信号的准确频率和幅值。依据周期性窄带干扰的频率差异,将图3中未与PD信号混叠的各类周期性干扰信号划为A、B、C区域,并提取染噪信号GSMM上的对应的区域子矩阵。通过搜索计算得出各区子域矩阵列(时间)向量上最大能量对应的频率点f1,f2,f3,…,fk,及对应该频率的列(时间)向量次数m1,m2,m3,…,mk。该区域上的周期性窄带干扰频率为
(9)
根据已求出的窄带干扰频率,通过搜索计算得出各区域矩阵对应行(频率)向量上各元素的能量值e1,e2,…,ek,该频段窄带干扰信号GSMM的能量值为
(10)
综合式(9)、式(10),再采用广义S逆变换[15]可得出窄带干扰一维时域信号特征量及其GSMMPk,Pk为M×N阶低秩矩阵。
基于传统S变换和广义S变换方法,通过区域最大能量法计算提取出图2染噪信号的周期性窄带干扰的特征量,并与原始仿真PD信号进行对比,见表2。结果表明由于广义S变换频域分辨率相对较高,可以使用区域最大能量法提取更准确的周期性窄带干扰特征量。
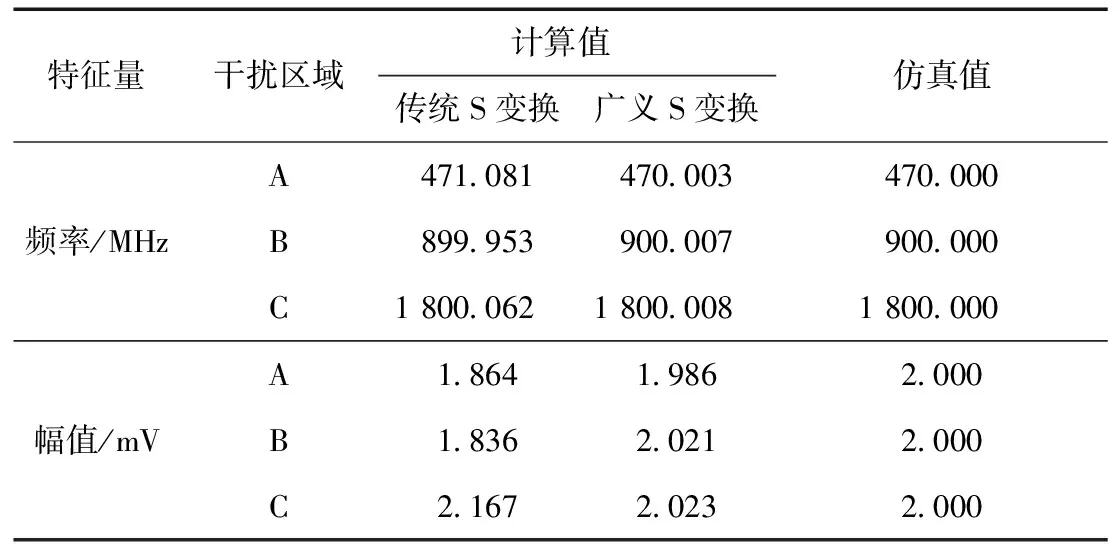
表2 周期性窄带干扰特征量计算结果
2.3 窄带干扰抑制方法
基于广义S变换的周期性窄带干扰抑制方法具体步骤为:
1)对UHF时域信号进行广义S变换,得到该信号的GSMMSM×N并绘制时频谱图。
2)根据UHF信号的时频谱图,将未与PD信号混叠的各类周期性窄带干扰信号区域化,并通过区域最大能量法计算得出窄带干扰频率和幅值。
3)根据周期性窄带干扰特征量得到相应的窄带干扰信号的GSMMP1,P2,…,Pn,采用矩阵逆向分离的方法得出消除窄带干扰后的信号GSMMWM×N为
(11)
4)对矩阵WM×N进行广义S逆变换,得出抑制窄带干扰后的PD信号。
根据上述方法对图1b信号进行去噪处理,去除窄带干扰后的局部放电时域信号和时频谱分别如图3所示。作为对比,基于传统S变换的去噪结果如图4所示。由于基于广义S变换模时频矩阵计算所得的周期性窄带干扰特征量更准确,使用矩阵逆向分离的方法可以更好地抑制窄带干扰,剩余干扰主要为高斯白噪声。而基于传统S变换去噪后的PD信号中仍含有部分周期性窄带干扰。
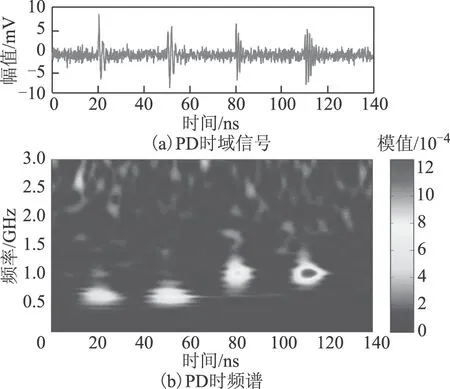
图3 基于广义S变换的周期性窄带干扰去噪结果Fig.3 Denoising results of periodic narrowband interference based on generalized S-transform

图4 基于传统S变换的周期性窄带干扰去噪结果Fig.4 Denoising results of periodic narrowband interference based on traditional S-transform
3 高斯白噪声抑制方法
为获得更准确的PD信号,需要对信号中残存的高斯白噪声进行抑制。奇异值分解(SingularValueDecomposition,SVD)去噪方法可以有效地抑制信号中的高斯白噪声。传统SVD去噪方法通过原始一维信号的连续截断和小波分解等方法构造SVD的轨迹矩阵,再对该矩阵进行SVD去噪[17]。基于一维时域信号的轨迹矩阵虽能有效反映信号的时域特征,但无法反映其频域特性,导致原始PD信号经过去噪处理后部分特征量失真。本文通过对原始一维信号进行广义S变换,获得PD信号的二维GSMM,选择含有更详细时频特征的二维GSMM作为轨迹矩阵,进行SVD去噪处理。
3.1 奇异值分解去噪方法
根据SVD理论[18],m×n阶的实数轨迹矩阵A的奇异值分解为
A=UΛVT
(12)
式中,U、V分别为m×m阶和n×n阶正交阵;Λ为对角矩阵,Λ=diag(a1,a2,…,an),其对角元素为A的奇异值,并按降序排列。
由于Λ是对角阵,因此SVD可将一个秩为k的m×n阶矩阵A表示为k个秩为1的m×n阶子矩阵的和。其中,每个子矩阵由2个特征矢量(分别来自于U和V)和权值相乘得到,即
(13)
式中,k为A的秩;ui、vi(i=1,2,3, …)分别为U和V的第i列奇异值矢量;ai为第i个奇异值;Ai为包含ui和vi的子矩阵。
在实际应用中,将染噪PD信号的GSMM分解到一系列奇异值和奇异值矢量对应的时频子空间中,矩阵A表示局部放电UHF信号的GSMM,相应的ui和vi分别表示频率和时间信息,而奇异值的大小则定量表示在该时频段信息量的大小。PD信号能量在时频谱图上分布集中,包含信息量分布相对较大;而高斯白噪声的能量在时频谱图上相对分散,包含信息量分布相对较小。故可以对信号进行SVD分解后提取信息量较大的奇异值,舍去信息量较小的奇异值,再进行信号的重构,达到抑制高斯白噪声的目的。信号重构公式为
(14)
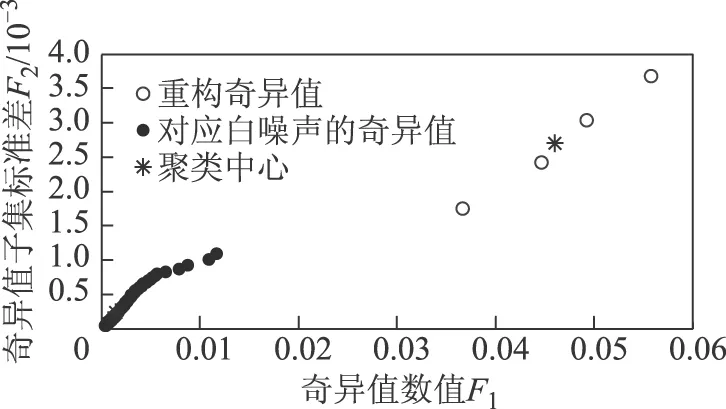
式中,Are为去噪信号的GSMM;j为选取含较大信息量奇异值的数量,且j 3.2 重构奇异值选择方法 根据上述分析,PD信号的SVD去噪算法的关键在于选择重构信号的奇异值数量j。如果重构奇异值数量选择较多,则SVD去噪效果不显著;重构奇异值数量选择较少,则易丢失PD信号部分特征量。对应PD信号的奇异值数值相对较大且分布分散,对应白噪声的奇异值数值相对较小且分布集中[19]。因此可以通过分析奇异值数值的大小和奇异值序列子集的离散度来选择重构奇异值。本文选择标准偏差作为子集离散度的评价参数,选择奇异值数值和奇异值子集标准偏差作为奇异值序列的特征量,通过K-means聚类算法[20]对奇异值序列进行分类并选择重构奇异值,具体步骤为: 1)基于广义S变换,得出含有白噪声的时频谱图GSMM,选择该矩阵作为轨迹矩阵进行SVD,得到奇异值序列a1,a2,…,an。 2)选择奇异值数值大小作为奇异值序列的特征量F1,F1=a1,a2,…,an。 3)建立基于奇异值序列的子集群,各子集ssi由集合中第n个到第i个奇异值元素组成,即ss1=[an,an-1, …,a1], …,ssi=[an,an-1, …,ai], …,ssn=[an]。 4)从ss1开始计算各子集的标准偏差stdi,选择各子集的标准偏差变成作为奇异值序列的另一个特征量F2,F2=std1,std2, …,stdn。 5)基于特征量F1和F2,使用K-means聚类算法对奇异值序列进行分类计算,分为对应PD信号和对应白噪声的两类,选择奇异值数值较大的分类为重构奇异值,得出重构奇异值个数j。 6)根据式(14)进行局部放电UHF信号的重构,通过广义S逆变换计算得出抑制高斯白噪声后的PD时域信号。 对图3信号进行上述方法的去噪处理,计算出的奇异值序列及其聚类结果如图5和图6所示。选取重构奇异值数量j=4。去除高斯白噪声后的局部放电UHF时域信号和时频谱如图7所示。结果表明,信号中的高斯白噪声得到了较好的抑制。 图5 奇异值序列Fig.5 Singular values 图6 奇异值序列K-means聚类结果Fig.6 K-means grouping results of singular values 图7 高斯白噪声去噪结果Fig.7 Denoising results of Gaussian white noise 作为参考,选用四种传统去噪方法对信号中的窄带干扰和白噪声干扰进行抑制。去噪方法及噪声类型见表3。其中,在基于小波变换方法二和方法三中,选用小波基的类型为db2和db8小波,且分解层数均为10层。为验证本文提出基于二维GSMM的SVD去噪方法有效性,选择传统一维SVD去噪方法对图3中PD信号的高斯白噪声进行抑制作为对比,记为方法四。各方法去噪结果如图8所示。 表3 传统去噪方法及噪声类型 图8 四种方法去噪结果Fig.8 Denoising results of four methods 引入信噪比(Signal Noise Ratio, SNR)、方均根误差(Root Mean Square Error, RMSE)、波形相似系数(Normalized Correlation Coefficient, NCC)、变化趋势参数(Variation Trend Parameter,VTP)四个去噪效果评价参数对各方法局放信号去噪效果进行评价。各评价指标具体定义及计算方法参见文献[21]。其中,SNR值越高表明对噪声的抑制能力越强;RMSE值代表去噪后PD信号与原始PD信号波形的偏差,其值越低表明信号畸变程度越低;NCC取值区间为[-1,1],且越接近1表明两种波形越相似;VTP代表两者波形变化趋势相似度,其值越接近1,两种波形变化趋势也就越相似。分别计算本文提出方法及上述四种对比方法的去噪效果评价参数,结果见表4。 表4 各方法去噪效果评价参数 对比分析图7、图8及表4,得出如下结论: 1)由于PD信号与周期性窄带干扰的频率出现混叠,采用自适应滤波器去噪虽然可以有效抑制窄带干扰,但会导致部分PD特征量丢失,使PD信号波形发生畸变。 2)由于周期性窄带干扰幅值高、信噪比低,传统的小波分解去噪方法无法准确区分PD信号与窄带干扰信号,会保留部分幅值较高的窄带干扰信号,而去除部分PD信号作为噪声干扰,导致信噪比较低及去噪后PD波形畸变。 3)本文方法相比传统一维信号去噪方法,噪声抑制效果更好且原始PD信号波形畸变较小。这是由于选择二维GSMM作为轨迹矩阵包含了更详细的信号局部时频特征,进行SVD后获得重构奇异值所对应的时频信息更完整,重构后可以得到更准确的原始PD信号。 图9为采用本文提出PD信号去噪方法去噪前、后各PD脉冲波形对比。结果表明,本文局部放电UHF信号去噪方法能够理想地恢复原始PD脉冲波形,信号波形无明显畸变失真,有利于后续分析。 图9 去噪前、后各PD脉冲波形对比Fig.9 PD pulses waveforms comparison before and after denoising 5.1 实验室信号去噪 为验证本文方法对实测PD信号去噪的有效性,在实验室中采用如图10所示的油中尖端和油中沿面放电模型来模拟绝缘缺陷,以获得实验室实测PD信号。两种放电模型均放入油浸式变压器内部进行油中加压试验,试验使用LB-530-NF UHF喇叭天线(工作带宽为0.5~3 GHz,最大增益为11 dBi)和Lecory WavePro 7Zi示波器(采样率为20 Gs/s,带宽为4 GHz)检测局部放电UHF信号。图11a和图11b为实验室中采用上述放电模型试验得到的两种PD信号实测波形。由于实验室实测信号信噪比较高,两种PD信号均加入频率分别为470 MHz、900 MHz、1 800 MHz,幅值分别为60 mV、20 mV的周期性窄带干扰,以及分布为(0,0.32)的高斯白噪声干扰。染噪后的PD信号波形如图11c和图11d所示。 图10 油中PD模型Fig.10 Models of PD in transformer oil 图11 实验室测量PD信号Fig.11 Laboratory measured PD signals 采用本文方法及传统方法(方法一~方法三)对上述含噪声的PD信号进行去噪处理,去噪结果如图12所示。由于原始PD测量信号噪声干扰较小,可将其近似等效为理想无噪PD波形,计算各方法去噪效果评价参数,结果见表5。 图12 实验室测量信号各类方法去噪结果Fig.12 Laboratory measured PD signals denoising results using each method 表5 实验室测量信号各类方法去噪评价参数 对比分析图12及表5,四种方法均能对实验室实测染噪局部放电信号进行噪声抑制,但采用传统方法的去噪结果信噪比较低,且波形有较大畸变;本文方法对噪声的抑制效果更好,波形无明显畸变,较好保留了原始局部放电信号局部特征,且去噪效果评价参数优于传统去噪方法。 5.2 现场检测信号去噪 本文对运行中的某220 kV敞开式变电站进行带电PD检测,检测使用设备与5.1节相同。图13为现场检测的两种含有干扰的UHF PD信号,现场存在较强的背景噪声,PD信号被严重干扰。采用本文提出的方法对该实测信号进行去噪处理。图14为使用本文方法和表3中传统方法(方法一~方法三)进行去噪处理后的PD信号。 图13 现场实测PD信号Fig.13 Actual measurement PD signals in field test 图14 现场实测PD信号去噪结果Fig.14 Denoising results of field measurement PD signals 由于无法测得不含噪声的原始PD信号,故不能使用上述的去噪评价参数对去噪效果进行评价。采用噪声抑制比ρNRR和幅值衰减比ρARR进行去噪效果评价,其定义为 (15) (16)式中,σ1、σ2分别为去噪前、后信号标准偏差;Am1、Am2分别为去噪前、后信号最大幅值。ρNRR反映了去噪前、后有效信号的凸显程度;ρARR反映了去噪前、后PD信号衰减程度。各类方法去噪结果的评价参数见表6。 结果表明,本文方法对现场局部放电UHF信号噪声抑制具有较好效果,与传统方法相比,可以更好地抑制各类噪声,且PD信号幅值衰减程度较低,有利于微弱PD信号检测。然而相对于传统去噪方法,本文提出的基于二维GSMM的去噪方法计算量较大,计算时间较长,对设备硬件配置要求较高。因此,需要对本文提出的去噪算法进行计算简化研究,提高其在现场检测中的适用性。 本文基于广义S变换模时频矩阵,结合区域最大能量法和奇异值分解去噪方法,实现了局部放电UHF信号中周期性窄带干扰和高斯白噪声的抑制。通过对仿真及实测信号进行噪声抑制处理,证明了该方法的有效性,得到以下结论: 1)在时频分析中,使用广义S变换比传统S变换可以获得更好的频域分辨率,采用区域最大能量法可以提取出更准确的窄带干扰的特征量,通过矩阵逆向分离可以更有效地去除窄带干扰。 2)仿真结果表明,基于二维模时频矩阵的奇异值分解去噪方法相比于传统一维时域信号的去噪方法,在更有效地抑制高斯白噪声的同时,去噪过程导致原始局部放电信号波形畸变小,较好地保留了信号特征,利于后续分析。 3)本文提出的去噪方法可以抑制实测PD信号中的周期性窄带干扰和高斯白噪声,具有较高的噪声抑制比和较低的幅值衰减比。 [1] 律方成, 金虎, 王子建, 等. 主分量稀疏化在 GIS 局部放电特征提取中的应用[J]. 电工技术学报, 2015, 30(8): 282-288. Lü Fangcheng, Jin Hu, Wang Zijian, et al. Principal component sparse and its application in GIS partial discharge feature eextraction[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 282-288. [2] Moore P J, Portugues I E, Glover I A. Partial discharge investigation of a power transformer using wireless wideband radio-frequency measurements[J]. IEEE Transactions on Power Delivery, 2006, 21(1): 528-530. [3] 侯慧娟, 盛戈皞, 姜文娟, 等. 基于信号模型参数辨识的变电站局部放电电磁波信号重构[J]. 高电压技术, 2015, 41(1): 209-216. Hou Huijuan, Sheng Gegao, Jiang Wenjuan, et al. Signal reconstruction for partial discharge electromagnetic wave in substation based on signal model parameters identification[J]. High Voltage Engineering, 2015, 41(1): 209-216. [4] 罗新, 牛海清, 胡日亮, 等. 一种改进的用于快速傅里叶变换功率谱中的窄带干扰抑制的方法[J]. 中国电机工程学报, 2013, 33(12): 167-175. Luo Xin, Niu Haiqing, Hu Riliang, et al. A modified method of suppressing narrow-band interference using fast fourier transform power spectrum[J]. Proceedings of the CSEE, 2013, 33(12): 167-175. [5] 唐炬, 黄江岸, 张晓星, 等. 局部放电在线监测中混频周期性窄带干扰的抑制[J]. 中国电机工程学报, 2010,30(13): 121-127. Tang Ju, Huang Jiang′an, Zhang Xiaoxing, et al. Suppression of the periodic narrow-band noise with mixed frequencies in partial discharge on-line monitoring[J]. Proceedings of the CSEE, 2010,30(13): 121-127. [6] KöPF U, Feser K. Rejection of narrow-band noise and repetitive pulses in on-site PD measurements[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1995, 2(3): 433-446. [7] 徐剑, 黄成军. 局部放电窄带干扰抑制中改进快速傅里叶变换频域阈值算法的研究[J]. 电网技术, 2004, 28(13): 80-83. Xu Jian, Huang Chengjun. Research on improved fast Fourier transform algorithm applied in suppression of discrete spectral interference in partial discharge signals[J]. Power System Technology, 2004, 28(13): 80-83. [8] Satish L, Nazneen B. Wavelet-based denoising of partial discharge signals buried in excessive noise and interference[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2003, 10(2): 354-367. [9] 唐炬, 樊雷, 卓然, 等. 用最优谐波小波包变换抑制局部放电混频随机窄带干扰[J]. 中国电机工程学报, 2013, 33(31): 193-201. Tang Ju, Fan Lei, Zhuo Ran, et al. Suppression of the random narrow-band noise with mixed frequencies in partial discharge with the optimal harmonic wavelet packet transform[J]. Proceedings of the CSEE, 2013, 33(31): 193-201. [10]Ma Xia, Zhou Chenke, Kemp I J. Interpretation of wavelet analysis and its application in partial discharge detection[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2002, 9(3): 446-457. [11]张宇辉, 段伟润, 李天云. 局部放电信号中抑制周期性窄带干扰的逆向分离方法[J]. 电工技术学报, 2015, 30(6): 232-239. Zhang Yuhui, Duan Weirun, Li Tianyun. A reverse separation method of suppressing periodic narrowband noise in partial discharge signal[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 232-239. [12]吴浩. 基于 S 变换样本熵的输电线路纵联保护新原理[J]. 电力系统保护与控制, 2016, 44(12): 15-22. Wu Hao. A new pilot protection principle based on S-transform sample entropy[J]. Power System Protection and Control, 2016, 44(12): 15-22. [13]Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. [14]Pinnegar C R, Mansinha L. The S-transform with windows of arbitrary and varying shape[J]. Geophysics, 2003, 68(1): 381-385. [15]易吉良, 彭建春. 基于广义S变换的短时电能质量扰动信号分类[J]. 电网技术, 2009, 33(5): 22-27. Yi Jiliang, Peng Jianchun. Classification of short-time power quality disturbance signals based on generalized S-transform[J]. Power System Technology, 2009, 33(5): 22-27. [16]尹柏强, 何怡刚, 朱彦卿. 一种广义S变换及模糊SOM网络的电能质量多扰动检测和识别方法[J]. 中国电机工程学报, 2015, 35(4): 866-872. Yin Baiqiang, He Yigang, Zhu Yanqing. Detection and classification of power quality multi-disturbances based on generalized S-transform and fuzzy SOM neural network[J]. Proceedings of the CSEE, 2015, 35(4): 866-872. [17]王振浩, 姚艳菊, 陈继开. 基于 SVD 方法的多台配电网静止无功补偿器交互影响分析[J]. 电力系统保护与控制, 2014, 42(7): 103-109. Wang Zhenhao, Yao Yanju, Chen Jikai. Interactions analysis of multiple DSVC controllers based on SVD method[J]. Power System Protection and Control, 2014, 42(7): 103-109. [18]Hou Zujun. Adaptive singular value decomposition in wavelet domain for image denoising[J]. Pattern Recognition Electrics and Electrical Insulation, 2003, 36(8): 1747-1763. [19]Ashtiani M, Shahrtash S. Partial discharge de-noising employing adaptive singular value decomposition[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2014, 21(2): 775-782. [20]Kanungo T, Mount D M, Netanyahu N S, et al. An efficient K-means clustering algorithm: analysis and implementation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(7): 881-892. [21]王永强, 谢军, 律方成. 基于改进量子粒子群优化稀疏分解的局放信号去噪方法[J]. 电工技术学报, 2015, 30(12): 320-329. Wang Yongqiang, Xie Jun, Lü Fangcheng. PD signal denoising method based on improved quantum-behaved particle swarm optimization sparse decomposition[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 320-329. (编辑 张洪霞) Partial Discharge Ultrahigh Frequency Signal Denoising Method Based on Generalized S-Transform Modular Time-Frequency Matrix LiuYushun1ZhouWenjun1LiPengfei1WangYong2TianYan2 (1.School of Electrical Engineering Wuhan University Wuhan 430072 China 2.Guangzhou Power Supply Bureau Co. Ltd Guangzhou 510620 China) In order to suppress the noise in the partial discharge (PD) ultrahigh frequency (UHF) signal, a denoising method based on generalized S-transform modular time-frequency matrix is proposed. Maximum local energy method was used to extract the characteristics of periodic narrow-band interference and cancel the interference through the matrix reverse separation based on two-dimension modular time-frequency matrix. In addition, singular value decomposition was used to suppress of Gaussian white noise in the PD signal. The denoising method presented in this paper was applied on the simulation and laboratory measured signals. Compared the denoising results with other four traditional denoising methods, the results show that the method presented in this paper suppressed the noise in the PD UHF signal effectively and retained more characteristics of PD signal. Compared with traditional methods, the denoising results of filed test signal validated the effectiveness of extracting PD signal with higher noise reduction ratio and lower amplitude reduction ratio. Partial discharge, denoising, generalized S-transform, narrow-band noise, maximum local energy method, white Gaussian noise, singular value decomposition 2016-01-22 改稿日期2016-07-26 TM835 刘宇舜 男,1990年生,博士研究生,研究方向为电力设备故障诊断。 E-mail:silencelys@163.com 周文俊 男,1959年生,教授,博士生导师,研究方向为高电压与绝缘技术。 E-mail: wjzhou@whu.edu.cn (通信作者)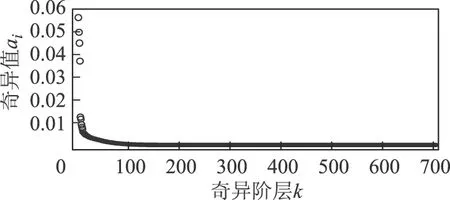

4 去噪效果对比分析


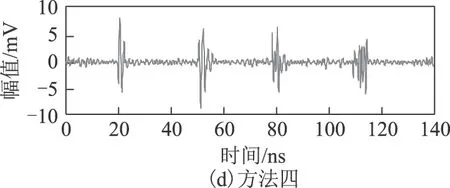
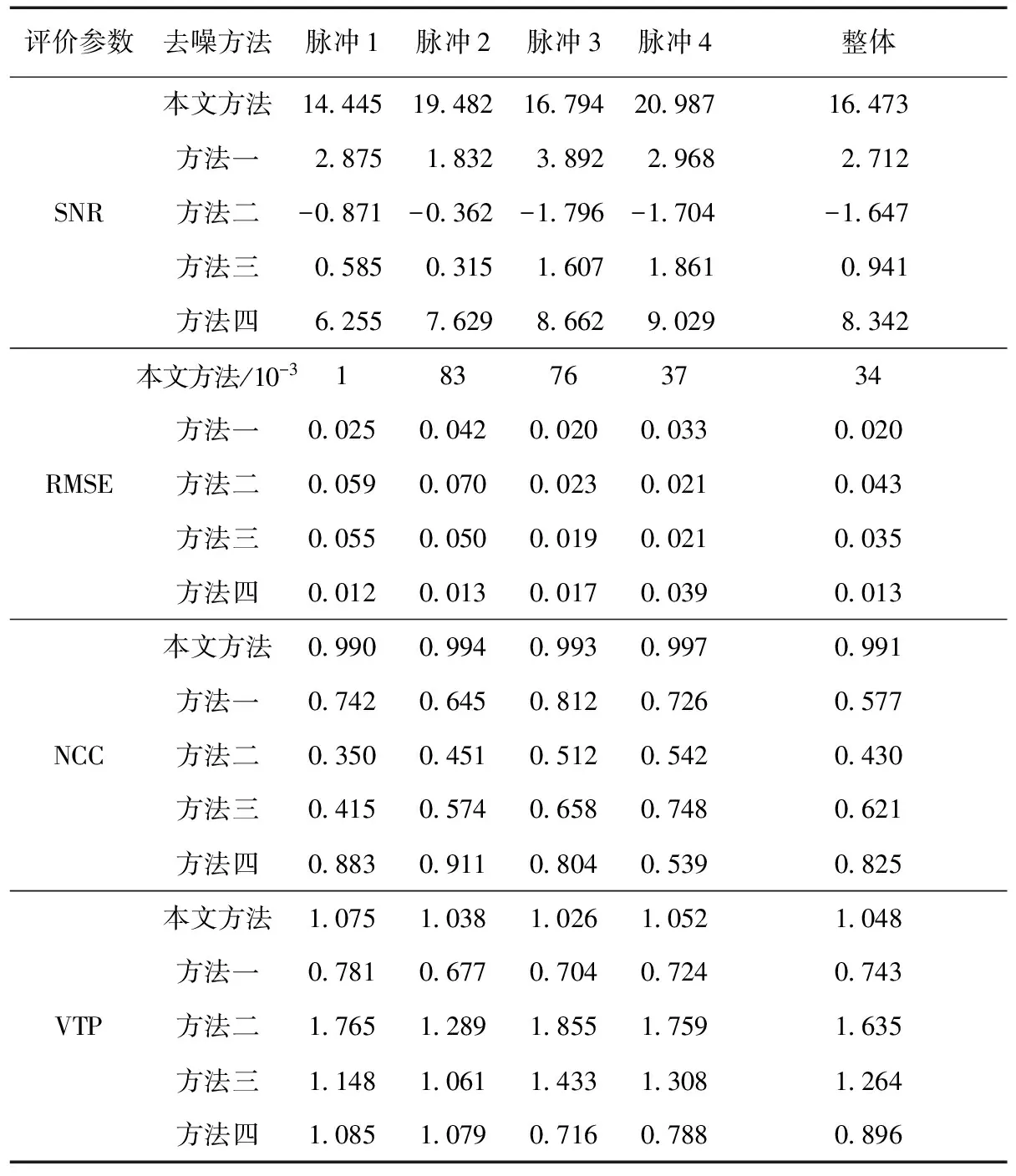
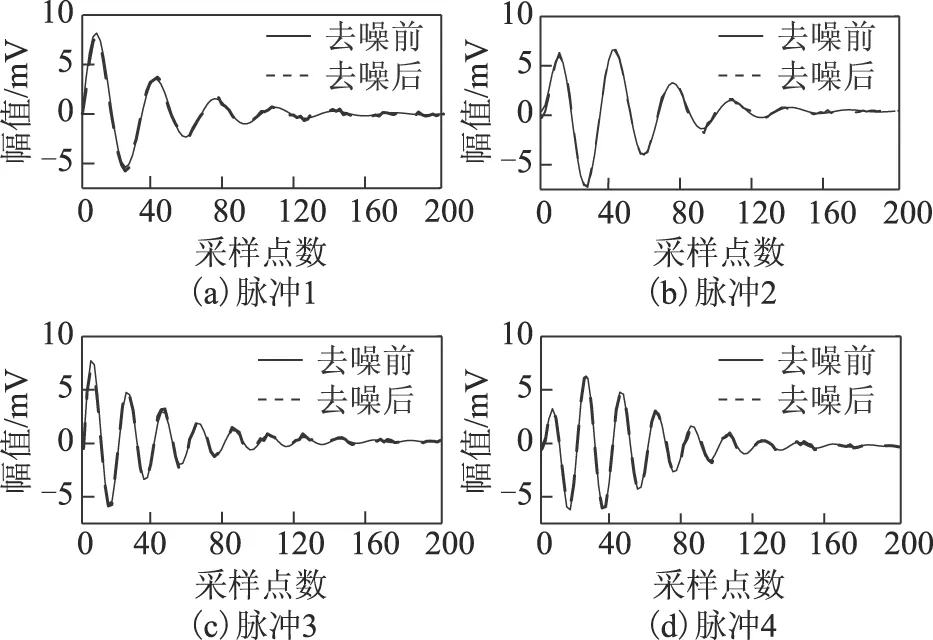
5 实测信号去噪
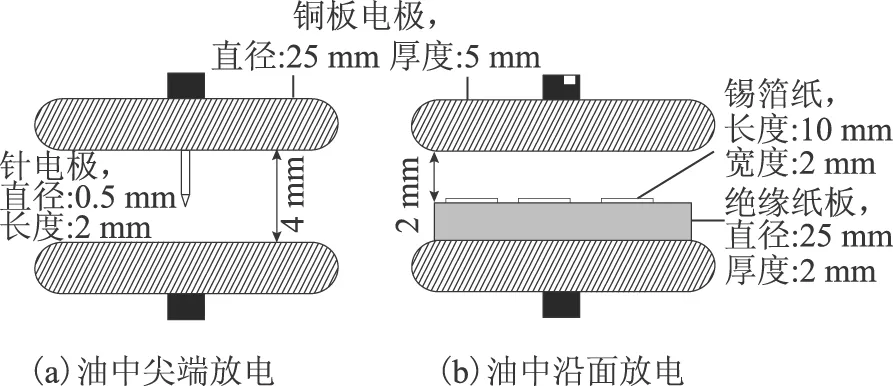
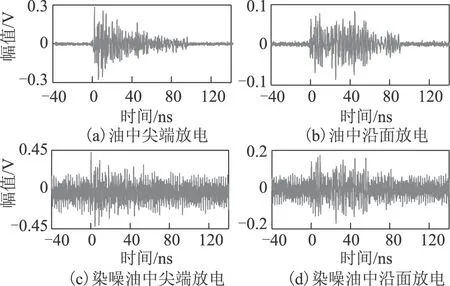

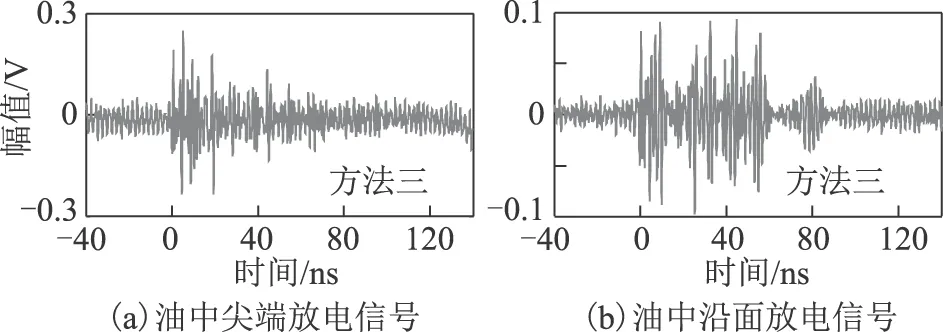
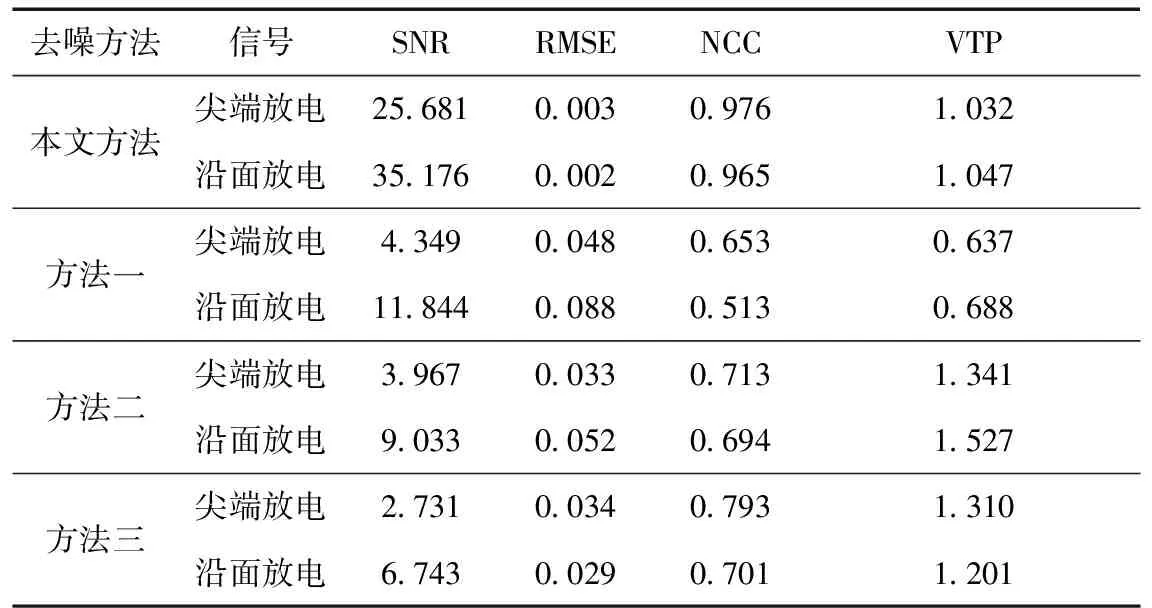

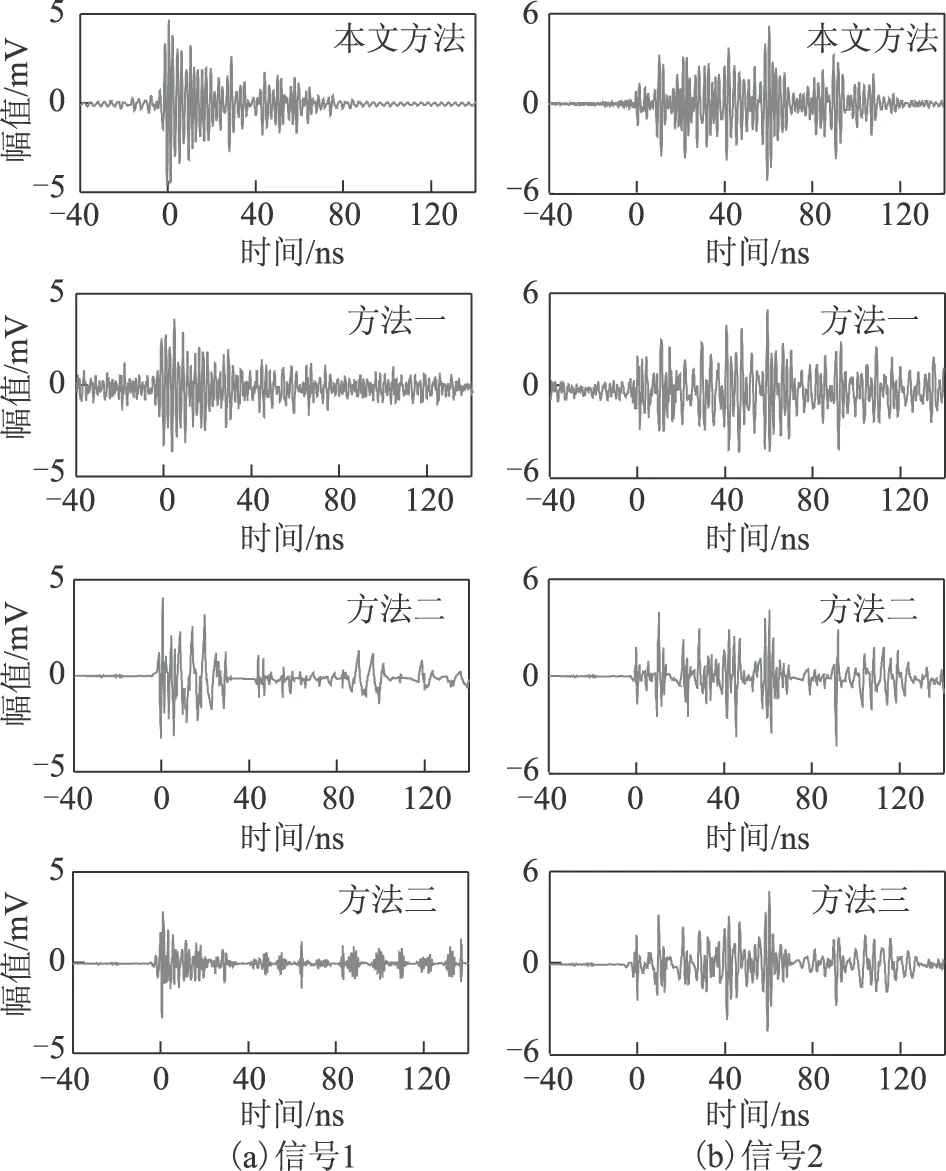
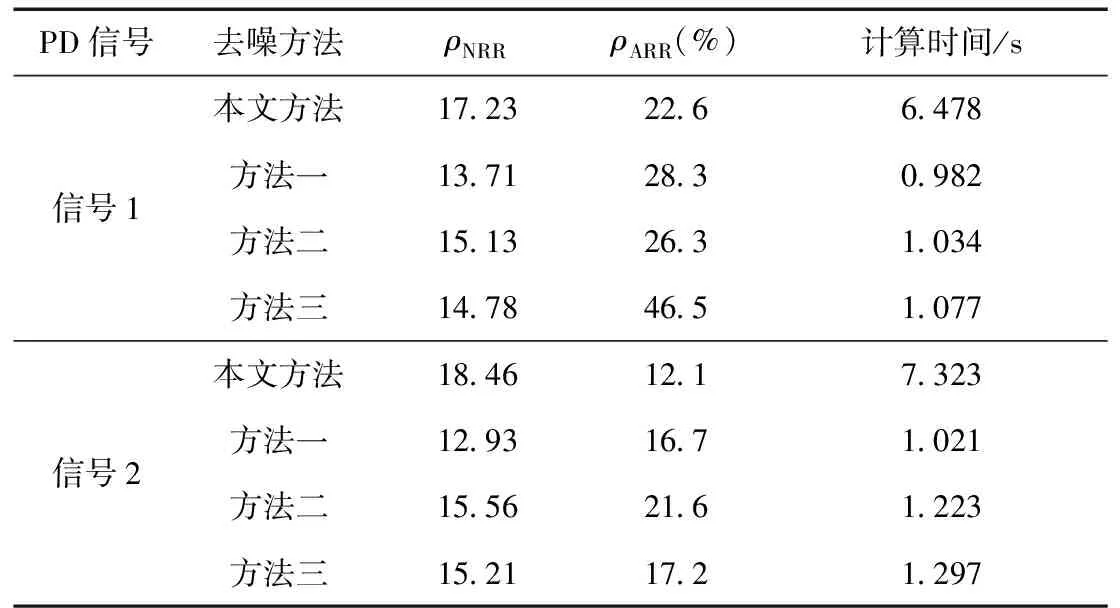
6 结论

