粒子群优化算法在工件排序问题中的应用
严坤妹
(福建商学院 基础部,福建 福州,350012)
粒子群优化算法在工件排序问题中的应用
严坤妹
(福建商学院 基础部,福建 福州,350012)
排序问题的求解和DCMST问题一样,一般是NP-hard的。度约束最小生成树(DCMST)问题按权矩阵W=(wij)n×n中wij是否等于wji可以分成两类,权矩阵是对称矩阵的DCMST问题已有很多启发式算法求解,其中有研究者提出了一种有效求解DCMST问题的模糊粒子群优化算法。针对工件排序问题,提出了应用粒子群优化算法求解排序问题的策略,并通过重新设计根树的prüfer数编码和初始粒子群的产生方法,使得基于prüfer数的模糊离散粒子群优化算法也能应用于权矩阵不是对称矩阵的DCMST问题的求解。
排序问题;根树;Prüfer数编码;粒子群优化算法;Hamilton路
0、引言
度约束最小生成树问题(Degree-Constrained Minimum Spanning Tree,DCMST)在实际应用中具有广泛的代表性,它是一个经典的NP-hard问题且难于用传统方法进行求解。DCMST问题的两个重要参数是:顶点个数和两个顶点之间的边代表的某种属性(权)。DCMST问题可以分成两类:权矩阵是对称矩阵的DCMST问题和权矩阵不是对称矩阵的DCMST问题。针对权矩阵是对称矩阵的DCMST,已有很多学者进行研究并提出了各种启发式算法。其中有学者研究了用遗传算法求解DCMST问题[1-2],也有学者详细讨论了用粒子群优化算法求解DCMST,并提出了一种有效的基于prüfer数求解DCMST的模糊离散粒子群优化算法[3]。本文在文献[3]算法的基础上,进一步研究权矩阵不是对称矩阵的DCMST的特点,重新设计粒子编码和修改初始种群的prüfer数的产生方法,使得基于prüfer数的模糊离散粒子群优化算法也能用于求解权矩阵不是对称矩阵的DCMST。针对工件排序问题,提出了应用粒子群优化算法求解排序问题的策略。
1.排序问题的数学模型
当不同型号的产品在某部机床上进行机械加工,若机床对某种型号产品加工完毕而要对另一种型号的产品进行加工时,通常工艺装备需要更换,即需要花费一定的工艺装备更换时间。产品的加工顺序不同,所花费的工艺装备更换时间的总和也就不同。因此,这个排序问题是要找一个不同类型产品的最优加工排序,使工艺装备更换时间的总和最少。例如某台机器必须加工多种工件J1,J2,…,Jn,在一种工件加工完毕之后,为了加工下一个工件,机器必须进行调整。不同工件的排序会影响调整时间,当工件的排序设定之后,在设备上就按此顺序进行加工。
对于工件排序问题,可以建立网络图,把不同型号的工件看作顶点,分别用1,2,3,…,n自然数表示,把不同工件间的调整时间看作两顶点之间连线的一种属性(权),并用正数wi,j表示。则排序问题可以转化为在对应的有向图中求一条权总数最小的有向哈密尔顿路(Hamiiton路)。
设在有向图G=(V,E,W)中,V={1,2,…,n)}表示工件的集合,代表图G的顶点;而E={e1,2,e1,3,…,e2,1,e2,3,…,ei,j,…,en,1,…,en,n-1}代表图G的边集合,ei,j≠ej,i,边ei,j表示工件i,j是否相继加工,若加工工件i后接着加工工件j,则图G对应的顶点i,j之间就有从i到j的边相连,即有向边ei,j=<i,j>存在,且令ei,j=1,否则ei,j=0。W=(wi,j)n×n是权矩阵,其中wi,j表示加工工件i后接着加工产品j所需要的设备调整时间,是边ei,j=<i,j>上的权;wj,i表示加工工件j后接着加工工件i所需要的设备调整时间,是边ej,i=<j,i>上的权,一般wj,i≠wi,j。如果有向图中任意两个顶点间都有弧,那么可以得到一个相应的竞赛图,由于每个竞赛图都有有向Hamiiton路,而有向Hamiiton路实际上就是一棵有向树(或根树)。设y=(y1,2,y1,3,…,yi,j,…,yn,1,…,yn,n-1)表示图G的一棵生成树(可以理解为有向树),其中如果边ei,j=1且被选中,则yi,j=1,否则yi,j=0(i=1,2,…,n;j=1, 2,…,n,i≠j)。因为一种工件加工完紧接着加工另一种工件,所以各个顶点的度约束不会大于2,即bi≤2(i=1,2,…,n),则排序问题可以转化为度约束最小生成树问题,对应的DCMST问题的数学模型如下所示:
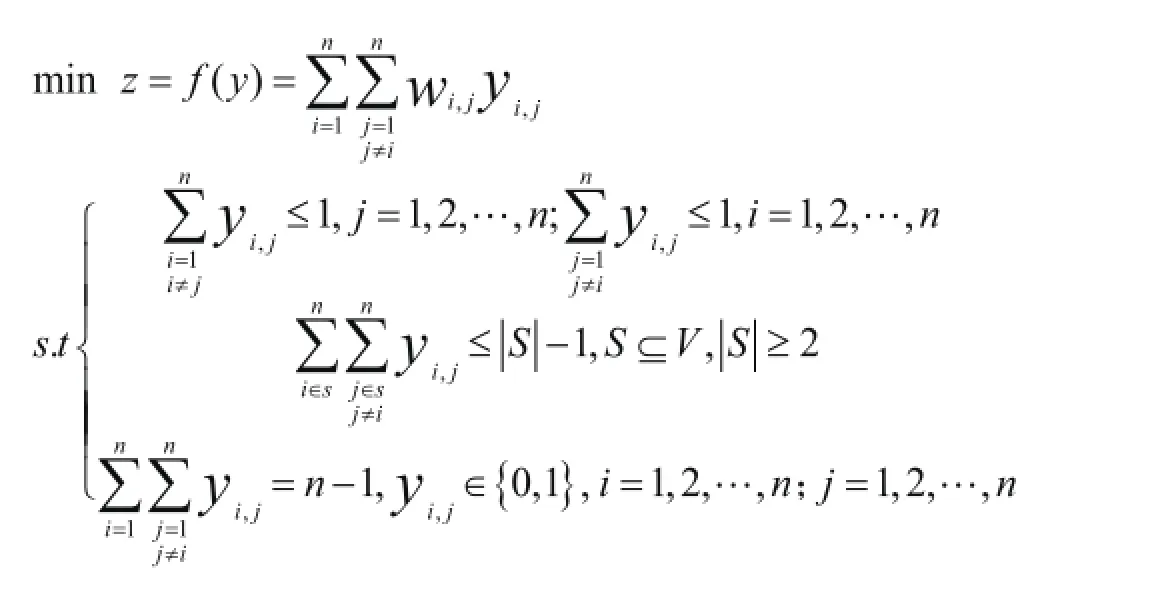
2.排序问题的求解策略
排序问题的求解,现在还没有十分有效的方法。若排序问题中的产品(如工件)个数与加工不同产品间的工艺装备更换时间是已知的,可以用整数规划的算法、最近邻居启发式算法等算法求解,但是计算量大。特别是当产品的种类较多时,这些算法的过程非常繁琐,甚至不能求解。所以希望有一个方法能得到一个相当好的解,但不一定是最优解。文献[3]提出的基于prüfer数的模糊离散粒子群优化算法用于求解权矩阵是对称的DCMST问题是有效的,且当DCMST问题中的顶点的度约束d≤2时,DCMST就是一棵线性树,对应的顶点排列就体现了顺序关系。而排序问题的网络图的权矩阵一般不是对称的,不能直接应用文献[3]提出的算法求解,需要对该粒子群优化算法进行适当修改。
对于一个实际的排序问题(如工件的排序),可以采用以下的策略解决:
第一步,把排序问题转化成有向图的有向hamilton路。构造具有顶点1,2,…,n(或v1,v2,…,vn)的有向图D=(V,E,W),其中有向边ei,j=<vi,vj>∈E,ej,i=<vj,vi>∈E,边上的权可以不相等,即wj,i≠wi,j。则D中必有有向hamilton路,而且不只一条,这些有向hamilton路实际上就是包含所有顶点的有方向的生成树,称为根树。
第二步,求D中的权数之和最小的有向hamilton路。利用求解权矩阵不是对称矩阵的DCMST的粒子群优化算法求出顶点的度约束为d≤2的根树,即权和最小的有向hamilton路,于是顶点的排序也就可知了。
3.权矩阵不是对称矩阵的DCMST的粒子群优化算法设计
文献[3]提出的基于prüfer数的模糊离散粒子群优化算法中,prüfer数编码是针对无向图G的权矩阵是对称矩阵的情形,选到的边与顶点顺序无关。如果权矩阵不是对称矩阵,选到的边就与顶点顺序有关,为了使该算法能求解权矩阵不是对称的DCMST问题(比如工件排序问题),需要重新设计根树的prüfer数编码和解码,并重新修改粒子群优化算法中初始粒子种群prüfer数的产生方法,而算法的具体设计流程与文献[3]一样,不再赘述。
3.1根树的prüfer数编码设计:
根树的prüfer数是指一棵有n个顶点的根树可以用n-1个数字的排列来表示,其中每个数字都是1和n之间的整数。
在一棵有n个顶点的根树中,用自然数1,2,…,n对顶点进行标号。
编码过程:将一棵根树(有序树))转化为一个Prüfer数
Step1:令j为根树T中入度是1,出度是0的顶点(即叶子顶点)中标号最大的顶点,i为j的关联顶点,即i是有向边eij=<i,j>的始顶点。则i为Prüfer数编码P的第一个数字,编码顺序从左到右。
Step2:删除根树T中的顶点j及边<i,j>。
Step3:重复上述步骤,直到剩下根顶点。于是得到一个由n-1个介于1和n之间的数字组成的数字排列,即为根树的Prüfer数。
解码过程:将一个Prüfer数转化为一棵根树
Step1:令P为原始Prüfer数,Q为所有不包含在P中的顶点的集合。
Step2:将Q中的顶点标号数字从左到右降序排列,保证Q的最左边的数字为最大数字。令i为P中的最左边的数字,j为Q中的最左边的数字(即最大数字)。将有向边<i,j>添加到树上,将i从P中除去,j从Q中除去。若i在P的剩余部分中不再出现,将i加入到Q中,始终保证Q中的数字按降序排列。
Step3:重复以上过程,直到P,Q中都无数字。于是形成n-1条边的有向树(根树)。
3.2初始种群prüfer数的产生方法
在求解DCMST问题的模糊离散粒子群优化算法中,如何产生prüfer数是很重要的环节。文献[3]的算法中用模糊矩阵R=(rij)m×n来产生无向图的生成树的prüfer数,其中n是顶点数目,m=n-2是prüfer数的总位数。为了产生根树的prüfer数,与文献[3]一样,也是通过构造模糊矩阵来产生的。设根树的顶点有n个,则根树对应的prüfer数的总位数为m=n-1。用[1,n]中的整数来表示一个有向图D的顶点,用X1,X2,…,Xn-1序列表示一棵有向树(根树)对应的prüfer数的各位数字。设X={X1,X2,…,Xn-1}表示prüfer数的各位数字的集合,Y={1,2,…,n}表示图的顶点的集合,构造一个(n-1)×n阶模糊矩阵R=(ri,j)(n-1)×n,rij∈[0,1],其中位于第i行第j列的元素ri,j,就代表prüfer数中第i位数Xi对于顶点j的隶属程度,采用最大数法得到prüfer数中第i位数字j,即若ri,j=max{Xi,1,Xi,1,…,Xi,n},则Xi=j(最大数法)。另外算法中的每个粒子位置和速度也都表示为一个(n-1)×n阶矩阵,即:
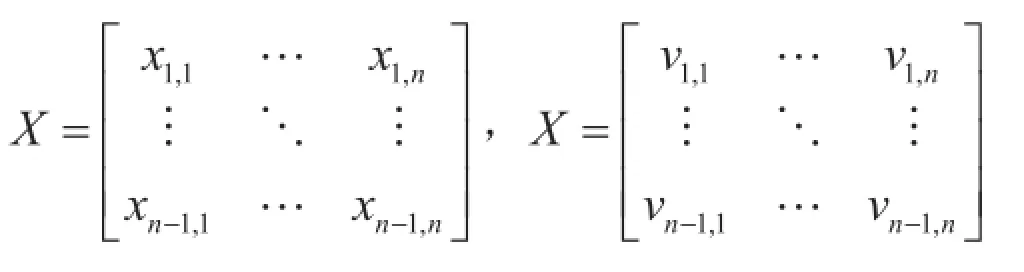
位置矩阵中行数表示粒子对应的prüfer数的总位数,列数代表图的顶点个数,prüfer数中的第i位数字Xi与顶点j的关系由元素xi,j决定。初始粒子种群由位置矩阵产生,初始化时位置矩阵中的元素按满足这两个条件随机产生;速度矩阵中的元素按满足这个条件随机产生。对位置矩阵的每一行按照最大数法进行解模糊就得到n-1个数字,即为初始粒子种群中粒子对应的prüfer数中的各位数字。
3.3适应度函数和度的改进
由于对粒子的位置矩阵进行解模糊后,得到的prüfer数表示的粒子可能有不满足度约束的粒子存在,另外,在迭代更新后的新一代粒子中也会出现不满足度约束的粒子,因此需要对粒子进行检验,看粒子是否可行,并对那些不满足度约束的粒子进行改进。如果顶点在prüfer数中出现的次数再加上1得到的数就是对应顶点的度数,若顶点没有在prüfer数中出现,则该顶点的度为1。因此把“顶点的度数不超过其规定的度的上限d”作为检验粒子是否可行的依据。如果某个顶点的度超过上限d,表示违反了度约束条件,那么将prüfer数中违反度约束的顶点随机替换为未在编码prüfer数中出现的顶点;如果粒子是可行的,则对prüfer数进行解码,便可得到一棵满足度约束的根树。经过这样修改后的模糊离散粒子群优化算法就可以解决有关排序问题。
4.粒子群优化算法求解排序问题的优点
粒子群优化算法因其概念简单、实现容易而引起学术界的广泛重视,一经提出便在短短的几年内出现了大量的研究成果。粒子群优化算法是非线性连续优化问题、组合优化问题和混合整数非线性优化问题的有效优化工具,是一种有效的全局搜索方法,目前已被应用于函数优化、神经网络训练、模糊系统控制、多目标优化及其他遗传算法的应用领域[4]。因此,当排序问题中产品的种类较多,即图的顶点个数较多、边数也较多时,可以把排序问题转化为DCMST问题,再用粒子群优化算法求解,不但可以缩短计算时间,而且能得到满意的最优解。
[1]牧云志,周根贵.基于prüfer数的遗传算法求解度约束最小树问题[J],计算机工程与应用,2008(12):53-56.
[2]宋海洲.求解度约束最小生成树的单亲遗传算法[J].系统工程理论与实践,2005(4):62-67.
[3]严坤妹,王镌,林娟,等.求解DCMST问题的模糊离散粒子群优化算法[J].莆田学院学报,2011(5):59-63.
[4]纪震,廖惠连,吴青华.粒子群算法及应用[M].北京:科学出版社,2009.
The Application of Particle Swarm Optimization Algorithm in Workpiece Sorting
YAN Kun-mei
(Foundation Department,Fujian Commercial College,Fuzhou 350012,China)
The solution of the sort problem,is similar to DCMST,which is generally NP-hard.The niche minimum spanning tree problem can be divided into two categories,the weight matrix has many heuristic algorithms for DCMST problem of symmetric matrix.Some researchers have proposed an effective fuzzy particle swarm optimization algorithm for DCMST problem.This paper proposes a strategy to solve the sorting problem by using particle swarm optimization algorithm,and then uses Prüfer number coding and primitive particle group generation method to apply to the solution of DCMST,which is weight matrix not symmetric matrix.
sorting problem;root tree;Prüfer number coding;particle swarm optimization algorithm;Hamilton path
O29
A
2096-3300(2017)02-0096-05
(责任编辑:杨成平)
2017-03-10
福建省教育厅科技项目“度约束最小生成树拓扑结构的粒子群算法研究”(JB10221)。
严坤妹(1966-),女,福建莆田人,副教授,硕士。研究方向:应用数学、计算智能及其应用。

