沥青混凝土水力劈裂的细观机理研究

武利强,王 良,章晓桦,朱 晟

(1.浙江省水利河口研究院,浙江杭州310020；2.河海大学水工结构研究所,江苏南京210098)

沥青混凝土水力劈裂的细观机理研究

武利强1,王 良1,章晓桦1,朱 晟2

(1.浙江省水利河口研究院,浙江杭州310020；2.河海大学水工结构研究所,江苏南京210098)

以基于离散单元法的二维颗粒流程序(PFC2D)为平台,建立可模拟沥青混凝土水力劈裂的数值模拟方法,深入研究沥青混凝土水力劈裂机理。该方法可模拟水力劈裂裂缝出现、扩展直到破坏的全过程。在此基础上,对沥青混凝土水力劈裂的细观机理和发生条件进行了研究。水力劈裂为拉伸破坏,细观机理为颗粒间法向接触力(拉力)超过法向粘结强度时,产生微裂缝,导致渗透系数增大,水压力急剧增长,从而激发更多微裂缝产生,直至微裂缝贯通形成宏观裂缝。发生条件为存在弱接触面区,有利于微裂缝的产生,而微裂缝产生后又可诱发更多裂缝产生直至贯通形成宏观裂缝。

离散单元法；沥青混凝土；水力劈裂；细观机理；发生条件

0 引 言

水力劈裂是土石坝破坏的主要因素之一,挪威Hyttejuvet坝[1]、英国Balderhead坝[2]、美国Teton坝[3]的失事均与水力劈裂密切相关。关于水力劈裂机理,目前有张拉破坏和剪切破坏两种说法[4,5],尚无统一说法。另外,关于水力劈裂的研究大多以粘土、岩体等为对象[6,7],沥青混凝土水力劈裂的研究则鲜见报道。随着沥青混凝土心墙高坝的增多,沥青混凝土心墙是否会发生水力劈裂已成为一个非常迫切需要研究的课题。然而,目前对水力劈裂的研究,不管是物理实验还是数值模拟及理论分析,多是从宏观的、基于现象学的角度进行研究,难以从本质上考虑水力劈裂过程中的非连续性及动态发展过程。

本文采用基于离散元原理的PFC2D(二维颗粒流程序)软件,建立了一套能够研究沥青混凝土水力劈裂的数值模拟方法。该方法能够从细观角度考虑水力劈裂过程的非连续性和裂缝的动态扩展性,为水力劈裂研究提供了一种新的方法和工具。在此基础上,研究了沥青混凝土水力劈裂的细观机理和发生条件。

1 研究方法

1.1 材料的力学模型

沥青混凝土组成成分包括沥青、骨料及孔隙等,不同组分力学性质差别较大,因此,不同组分应采取不同的力学模型表征。本文将沥青混凝土假定为三相材料,即粗骨料、沥青玛蹄脂及孔隙。各相材料的力学模型[8]分别为①骨料颗粒之间采用线性接触刚度模型、滑动模型；②沥青马蹄脂之间、沥青马蹄脂与骨料颗粒之间采用Burger’s模型、接触粘结模型和滑动模型 。

1.2 流体模型

流体模型以沥青混凝土模型为基本框架,添加流体域单元,流体域单元可以储存流体,相邻流体域单元之间的流体交换符合流体流动方程。

几何上,流体域单元是固体颗粒相互连接构成的封闭区域；力学上,流体域单元内具有流体压力,且在该封闭区域内均匀分布,流体压力直接作用在构成该流体域单元的固体颗粒上,如图1a所示。不同流体域单元之间,通过“管道”进行流体交换(如图1b所示),“管道”内流体运动符合流体运动方程,“管道”长度为L,即两流体域单元形心之间的距离,宽度为a,即裂缝宽度。沥青混凝土由于孔隙很小,材料粘性较大,因此流体的速度较小,为层流状态,则流体流动符合立方定律,流动方程为

(1)

式中,k为水力传导系数；Δp为压强差；L为“管道”长度；a为“管道”宽度。

一个时步内,流体压力的变化值为

(2)

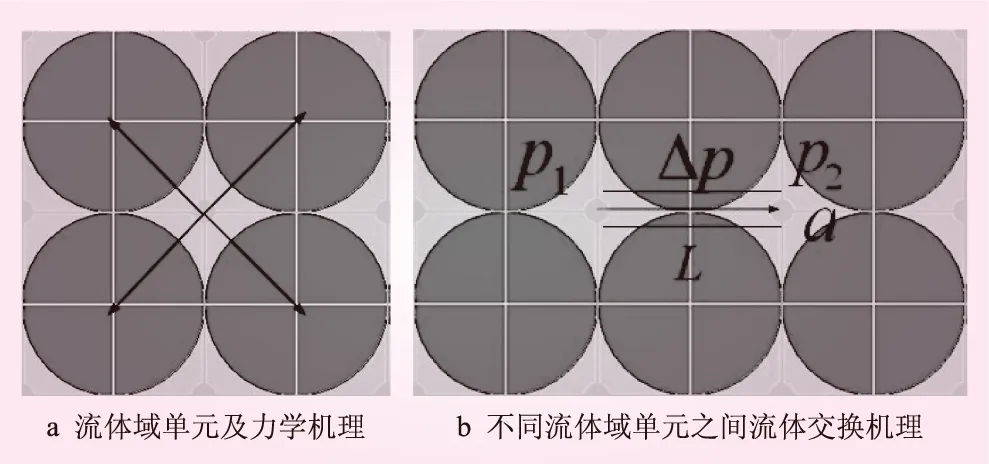
图1 流体域单元力学机理

式中,Kf为流体体积模量；Vd为流体域单元体积；ΔVd为流体域单元力学机理意义上的体积变化。

1.3 流固耦合机理

流固耦合的本质为流固间的相互作用,最终表现在力与位移上,具体为：①颗粒接触力的变化,引起颗粒之间距离a的变化,进而影响流量q；②流量q变化,相邻流体域单元间压力差的变化,进而影响流体域单元的流体压力；③流体域单元的流体压力作用于组成域单元的颗粒上,从而改变颗粒接触力大小。

1.4 模型参数

参数确定方法为标定系数法,即将数值模拟试验曲线和实际物理试验曲线进行拟合,当二者一致时的模型参数即代表了该种材料的参数。为此,特选取单轴压缩试验和常规三轴压缩试验,试验用料为三峡茅坪溪沥青混凝土心墙料,沥青混凝土最大粒径为20 mm,级配指数为0.35(见图2),沥青用量6.5%,孔隙率1.41%,试样尺寸为Ф40 mm×80 mm,数值试样见图3。曲线拟合结果见图4,参数取值见表1和表2。

图2 集料级配曲线

图3 沥青混凝土数值试样

图4 应力-应变试验曲线拟合

表1 力学模型参数

表2 流体模型参数

2 水力劈裂分析

2.1 试验过程

试验用料为茅坪溪沥青混凝土心墙料,试样直径为100 mm,高度为200 mm。待试样在规定的温度下养护48 h后,在试样的一端中心处采用立钻钻孔,孔径为20 mm,孔深为160 mm。在无围压的情况下进行水力劈裂试验,劈裂前后试样见图5。

图5 沥青混凝土水力劈裂试验

2.2 试验结果分析

2.2.1 与物理试验结果比较

物理试验无围压情况下,劈裂压力为1.20 MPa,数值模拟的劈裂压力为1.10 MPa。模拟值与试验值差别的主要原因是本文假定颗粒之间密集接触,一定程度上弱化了初始孔隙的影响,使试样干密度比实际值偏大,因此模拟值比实际值偏大,而本文并不是完全定量研究,更多的是对劈裂机理的研究,因此存在一定的误差是可以接受的。

2.2.2 水力劈裂机理

由图5d可知,裂缝走向不规则,基本沿骨料和沥青结合面分布,这与粘土劈裂不同,粘土试样中,裂缝走向基本呈直线或折线[7]。原因是粘土材料比较均一,而沥青混凝土是典型的多相复合体,骨料和沥青的刚度相差较大,因此在结合面易产生应力集中现象,而骨料一般不会破碎,因此裂缝易沿着结合面分布。

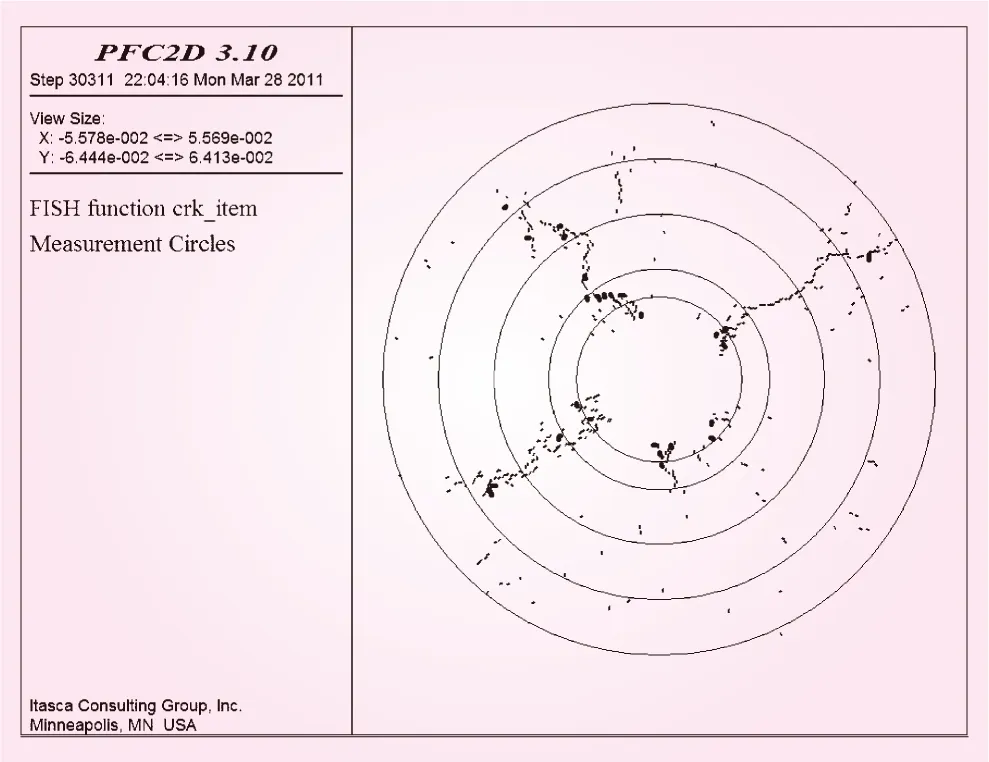
图6 水力劈裂微裂缝破坏类型

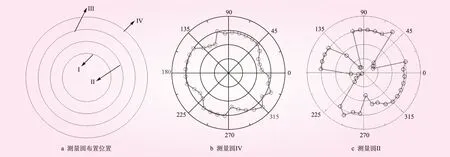
图7 初始法向接触力均值分布

颗粒之间粘结破坏后形成一个微裂缝,拉伸破坏的微裂缝标记为细短线,剪切破坏的微裂缝标记为粗断线,见图6。可见,沥青混凝土水力劈裂微裂缝绝大部分为拉伸破坏,微裂缝贯通后即形成宏观裂缝。至此,沥青混凝土水力劈裂的细观破坏机理可表述为：颗粒间的法向接触力(拉力)超过法向粘结强度,在颗粒之间形成微裂缝,当微裂缝贯通后,试样即发生水力劈裂破坏。

2.2.3 水力劈裂发生条件

由水力劈裂机理可知,微裂缝的破坏基本是拉伸破坏,因此,颗粒间的法向接触力是一个重要指标。为进一步研究劈裂的发生条件,测量了劈裂试样不同尺度范围内法向接触力均值,测量范围及结果见图7。图7b为测量圆Ⅳ(整个试样范围)内法向接触力均值分布,最大值为2.96 kN,最小值为2.49 kN,相差15.8%；图7c为测量圆Ⅱ(局部范围)内的法向接触力分布,最大值为3.01 kN,最小值为1.66 kN,相差44.8%。两个测量范围内,法向接触力均值在25°～45°、105°～135°和180°～225°范围内低于其他范围的值,尤其在局部小范围内,此现象更加明显。这些区域即通常意义的弱接触面区,图7d显示劈裂裂缝的位置与弱接触面的位置是一致的。

水力劈裂试验中,随着水压的逐步增大,试样的应力状态由初始的受压逐渐变为受拉,当拉应力大于法向粘结强度时,粘结破坏,微裂缝出现。显然,弱接触面区成为最早产生微裂缝的区域。而微裂缝的产生将使渗透系数急剧增大。由达西定律知：

q=KFΔh/L

(3)

式中,K为渗透系数；F为过水断面；Δh为渗流路径上的水头损失,大小为Δp/γ；L为渗流路径长度。

联立式(1)并将F=at(其中,t为单位长度)代入式(3),可得渗透系数K的表达式

K=ka2γ

(4)

由式(4)系数K的大小与k、a、γ有关,k、γ为流体的固有属性,劈裂过程中保持不变,因此影响K的主要因素是a。微裂缝产生后,a将变大,则K将呈平方式的增长,水压力也会相应增长,从而激发裂缝附近产生更多裂缝,形成连锁反应,最终形成贯通的宏观裂缝。

4 结 论

(1)沥青混凝土水力劈裂为拉伸破坏,细观机理为：颗粒间法向接触力(拉力)超过法向粘结强度时,产生微裂缝,导致渗透系数增大,水压力急剧增长,从而激发更多微裂缝产生,直至微裂缝贯通形成宏观裂缝。

(2)沥青混凝土水力劈裂发生条件为：试样存在弱接触面区,当水压足够大时,微裂缝首先在这些区域形成。一旦形成,就会发生连锁反应,直到宏观裂缝形成,劈裂破坏为止。

[1]KJAERNSLI B, TORBLAA L. Leakage through Horizontal Cracks in the Core of Hyttejuvet Dam[R]. Nowregian Geotechnical Institute, Oslo, Norwag, 1968: 39-47．

[2]VAUGHNA P R, KLUTH D J, LEONARD M W, et al. Cracking and Erosion of the Rolled Clay Core of Balderhead Dam and the Remedial Works Adopted for Its Repair[C]∥10th International Congress on Large Dams, Montreal, Canada, 1970: 73-79．

[3]SEED H B, DUNCAN J M. The Teton Dam Failure, A Retrospective Review[C]∥Proeeedings of the 10th ICSMEF, 1981: 219-238．

[4]JAWOSKI W, DUNCAN J M, SEED H B. Laboratory study of hydraulic fracturing[J]. Journal of the Geotechnical Engineering Division, 1981, 107(6): 713-732．[5]孙亚平. 水力劈裂机理研究[博士学位论文[D]. 北京: 清华大学, 1985．

[6]曾开华. 土质心墙坝水力劈裂机理及影响因素的研究[D]. 南京: 河海大学, 2001．

[7]孔宪勇. 土石坝心墙料水力劈裂特性试验研究[D]. 武汉： 长江科学院,2009．

[8]万连宾, 朱晟. 沥青混凝土轴心受压试验的计算机辅助方法应用[J]. 水力发电, 2014, 40(4): 46-49．

(责任编辑 王 琪)

Study on Meso-mechanism of Hydraulic Fracture of Asphalt Concrete

WU Liqiang1, WANG Liang1, ZHANG Xiaohua1, ZHU Sheng2

(1. Zhejiang Institute of Hydraulics and Estuary, Hangzhou 310020, Zhejiang, China;2. Institute of Hydraulic Structures, Hohai University, Nanjing 210098, Jiangsu, China)

For understanding the mechanism of hydraulic fracture of asphalt concrete, a numerical method used to simulate hydraulic facture of asphalt concrete is suggested based on Two-dimensional Particle Flow Code (PFC2D). The method can reproduce whole process of hydraulic facture which includes the appearance, propagation and fracture of crack. Then, the meso-mechanism and occurred conditions are studied. The results show that the hydraulic fracture fails in tension. When the normal contact force is larger than the bond strength, the micro crack appears which can lead to the increasing of permeability coefficient. As a result, water pressure adjacent to micro crack will increase, which induces more micro cracks. Many connected micro cracks finally will form macrosopic cracks. The occurred condition of hydraulic fracture is the existence of weak contact surface regions where the first micro crack will appear．

discrete element method; asphalt concrete; hydraulic facture; meso-mechanism; occurred condition

2016-07-19

国家自然科学基金项目(51609215)；浙江省水利河口研究院博士后基金项目(质检A15001)

武利强(1985—),男,河北石家庄人,工程师,博士,研究方向为水工材料．

TV431.5

A

0559-9342(2017)02-0047-04