三维Navier-Stokes方程在Morrey空间的正则性准则
王玉田,迟美玲,李心亮
(山东理工大学 理学院,山东 淄博 255049)
三维Navier-Stokes方程在Morrey空间的正则性准则
王玉田,迟美玲,李心亮
(山东理工大学 理学院,山东 淄博 255049)
在三维欧式空间中研究了Navier-Stokes方程弱解的正则性准则,利用能量估计的方法以及几类不等式,在Morrey空间中得到了关于形张变量分量的正则性准则.
Navier-Stokes方程;正则性准则;Morrey空间;形张变量分量
(1)
式中u=u(x,t)表示速度场;p=p(x,t)表示压力项;u0(x)表示给定的初始速度场且在分布意义下满足·u0=0.
Leray[1]与Hopf[2]证明了:若初值u0∈L2(3),则方程(1) 存在弱解u∈L(0,;L2(3))∩L2(0,;H1(3)),这个弱解被称为Leray-Hopf弱解.然而,这个弱解的正则性和唯一性仍然是具有挑战性的公开问题.
Serrin[3]提出了如果弱解u(x,t)满足u(x,t)∈Lp(0,T;Lq(3)),其中<,,则这个解满足u(x,t)∈C((0,T)×R3).
BeiraodaVeiga[4]证明了,如果Leray-Hopf弱解满足ω(x,t)∈Lp(0,T;Lq(3)),其中<,<,那么u(x,t)在(0,T)上是整体的强解.
在过去的几年中,关于速度场梯度分量的正则性准则被众多学者进行了研究[5-11].
Zhou[12]得到了涉及一个分量的正则性准则,如果<,则弱解在(0,T)上是光滑解.
在文献[13]中, 作者得到如下涉及一个分量的正则性准则].
本文在这个方向上进行进一步的探究,利用能量估计的方法以及几类不等式,在Morrey空间中得到了关于形张变量分量的正则性准则.
定理1 设T>0,u0∈H1(3)且·u0=0,u(x,t)是方程(1)在[0,T]上的弱解,其中初值为u0. 若
(2)
式中r∈[0,1],j=1,2,3
则弱解u(x,t)在[0,T]×3上是强解.
1 预备知识
Morrey空间的定义和性质如下:
定义1 若1 引理 1[14]若 0≤r≤1,则有如下不等式 为了证明定理1,首先对方程的光滑解作一些先验估计. 引理2 设T>0,u0∈H1(3),且在分布意义下是方程(1)在[0,T)上的弱解,其中u0是初值. 若速度场梯度满足条件(2),则有 (3) 由分部积分,可得 (4) 下面逐项估计(4)式的右边. (A) 当i=j=3时, C‖σ33hu‖2‖hu‖2≤ (B) 当i=j=k(1,2)时, (∂1u1)(∂2u2))dx≤ (C) 当i≠j=k(1,2)时, (D) 当(i=k≠j)+(i=j≠k)(1,2)时, (E) 当(3=i≠j)+(3=j≠i)时, 综合(A)-(E),可得如下不等式, 利用Gronwall不等式,可得 因此,若u满足条件(2),则引理2得证. 引理3 若T>0,u0∈H1(3),且在分布意义下·u=0.假设是方程(1)在[0,T]上的弱解,且初值为u0.若速度场梯度满足条件(2), 则有 证明 在空间L2(3) 中,方程(1)两边同时乘上-Δhu,得到 显然 由引理2的证明可知,只需估计右式的第二项.由分部积分可得 (5) 下面逐项估计(5)式的右边. (A)当(i=3≠j)+(j=3)时 (B) 当(i,j≠3)时, 综合(a),(b)以及引理2的证明过程,可以得到如下不等式 由Gronwall不等式,得到 因此,若u满足条件(2),则引理3得证. 利用强解和弱解的经典理论,结合引理2和引理3,证明了定理1. [1]LERAYJ.Surlemouvementd’unliquidevisqueuxemplissantl’espace[J].ActaMath,1934,63(1): 193-248. [2]HOPFE. ÜberdieAnfangswertaufgabefürdiehydrodynamisGrundgleichungen[J].MathNachr, 1950,4(1-6): 213-321. [3]SERRINJ.OntheinteriorregularityofweaksolutionsoftheNavier-Stokesequations[J].ArchRationMechAnal, 1962,9(1): 187-195. [4]VEIGA.AnewregularityclassfortheNavier-StokesequationsinRn[J].ChineseAnnMath, 1995,16(4): 407-412. [5]ZHOUY.OneregularitycriteriaintermsofpressurefortheNavier-StokesequationsinR3[J].MathematischeAnnalen, 2006,328(1):173-192. [6]CAOCS,TITIES.Globalregularitycriterionforthe3DNavier-Stokesequaitonsinvolvingoneentryofthevelocitygradienttensor[J].ArchRationMechAnal, 2011,202(3): 919-932. [7]ZHOUY,FANJ.Logarithmicallyimprovedregularitycriteriaforthe3DviscousMHDequations[J].ForumMathematicum,2012,24(4):961-708. [8]GALAS,RAGUSAM.AnewregularitycriterionfortheNavier-Stokesequationsintermsofthetwocomponentsofthevelocity[J].ElectronicJournalofQualitativeTheoryofDifferentialEquations,2016,26:1-9. [9]ZHANGZJ.Aremarkontheregularitycriterionforthe3DNavier-Stokesequationsinvolvingthegradientofonevelocitycomponent[J].JMathAnalAppl, 2014,414(1): 472-479. [10]ZhangH.Anewregularitycritierionforthe3DNavier-Stokesequations[J].JounalofAnhuiUniversity, 2012,36(5): 12-15. [11] 张辉.三维Navier-Stokes方程的正则性准则[J].应用数学与计算数学学报,2015,29(4):423-430. [12]ZHOUY.AnewregularitycriterionforNavier-Stokesequationsintermsofthegradientofonevelocitycomponent[J].MethodsApplAnal, 2002,9(4): 563-578. [13]ZHOUY,POKOMYM.OnaregularitycritierionfortheNavier-Stokesequationsinvolvinggradientofonevelocitycomponent[J].J.Math.Phys., 2009, 50(12): 767-769. [14]MachiharaS,OzawaT.InterpolationinequalitiesinBesovspaces[J].Proc.Amer.Math.Soc. ,2002,13(5):1 553-1 556. (编辑:刘宝江) A regularity criterion for the 3D Navier-Stokes equations in the Morrey spaces WANG Yu-tian, CHI Mei-ling, LI Xin-liang (School of Science, Shandong University of Technology, Zibo 255049, China) The regularity criterion for weak solutions to the 3D Navier-Stokes equations is studied. By the energy method and some inequalities, one regularity criterion in terms of one component of the deformation tensors in Morrey spaces is obtained. Navier-Stokes equations; regularity criterion; Morrey space; one component of the deformation 2016-09-20 王玉田, 女, 15165339057@163.com 1672-6197(2017)04-0076-03 O A



2 定理1的证明










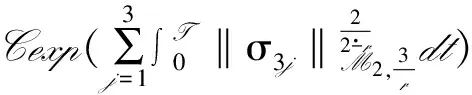








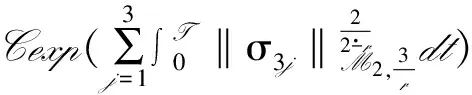
——我美丽的家园

