防止OFDM天线放大器峰值削波的AMAPR帧加权方法

范晓晶，张 珅

(1.合肥工业大学 工程训练中心，安徽 合肥 230601；2.华为软件技术有限公司,江苏 南京 21001)

防止OFDM天线放大器峰值削波的AMAPR帧加权方法

范晓晶1，张 珅2

(1.合肥工业大学 工程训练中心，安徽 合肥 230601；2.华为软件技术有限公司,江苏 南京 21001)

OFDM系统由于子载波数目庞大，具有较大的动态信号范围和非常高的峰均功率比(PAPR),往往造成天线放大器的非线性失真和峰值削波,从而增加系统的误码率。较为先进的算法是利用峰值因数PAR对输入信号进行加权，降低了峰均功率比PAPR，但该算法使得输入信号大幅衰减，信噪比迅速减小，误码率增加。基于上述问题，提出新的，利用AMAPR(信号峰值与天线放大器极大值比)进行帧加权的计算方法，当某一帧最大功率大于放大器的线性区间，再对该帧实现线性补偿方法。逐帧计算加权系数，尽最大可能提高输入信号的信噪比。通过仿真，验证了AMAPR帧加权算法能防止峰值削波，改进误码率性能，防止信号的大幅度衰减，实现了低成本天线放大器的线性补偿。

信号峰值与天线放大器线性极大值比；正交频分复用多载波调制；线性补偿；峰值削波

0 引言

正交频分复用多载波调制技术(OFDM)[1]提供了相当高的频谱效率，多径时延扩展，抗频率选择性衰落渠道与动力效率。因此，OFDM技术用于高数据速率通信，并已广泛部署在许多无线通信标准如数字视频广播(DVB)[2]和无线移动领域。由于子载波数目庞大，OFDM系统具有较大的动态信号范围，非常高的峰均功率比(Peak-to-Average Power Ratio,PAPR)[3]。在现代无线通信系统中，高PAPR往往会造成天线放大器的非线性失真和峰值削波，从而增加系统的误码率。

解决这个问题的常用方法是通过硬件改进，例如选用更为复杂、昂贵的功率放大器和发射天线，保证它工作在线性区域。但是不幸的是，这种解决方案为实现大范围的线性特征，并保证足够的区域覆盖，通常需要大功率放大器和高功率天线，难以实现终端小型化，并使系统成本大大增加。

为了节约成本并实现天线的小型化，软件改进算法成为研究的热点。目前较新的算法多是基于PAPR,利用峰值因数PAR(Peak-to-Average Ratio)[4]对放大器的输入信号进行加权，已达到降低了PAPR的目的[5]。但是在实际实现过程中, 如果峰值因数PAR过大[6]，加权后的输入信号并不能杜绝峰值削波的发生并保证放大器输入信号工作的线性范围，其所带来的负作用使输入信号大幅衰减，信噪比迅速减小[7]，造成输出端误码率大大增加。

为了保证输入信号工作在放大器的线性区间，同时解决信噪比迅速减小的矛盾，本文创造性地提出了基于信号峰值与天线放大器线性极大值比(AMAPR)的帧加权算法，只有当某一帧最大功率大于放大器的线性区间，才对该帧实现线性补偿方法，逐帧计算加权系数[8]，保证输入信号工作在线性范围，从而提高了输入信号的信噪比，防止峰值削波，防止信号的大幅度衰减。

1 定义AMAPR——信号峰值与天线放大器线性极大值比

图1显示了功率放大器的输入输出特征。当输入功率大于PMax时,放大器的输出便进入非线性区域， 输出便会失真。

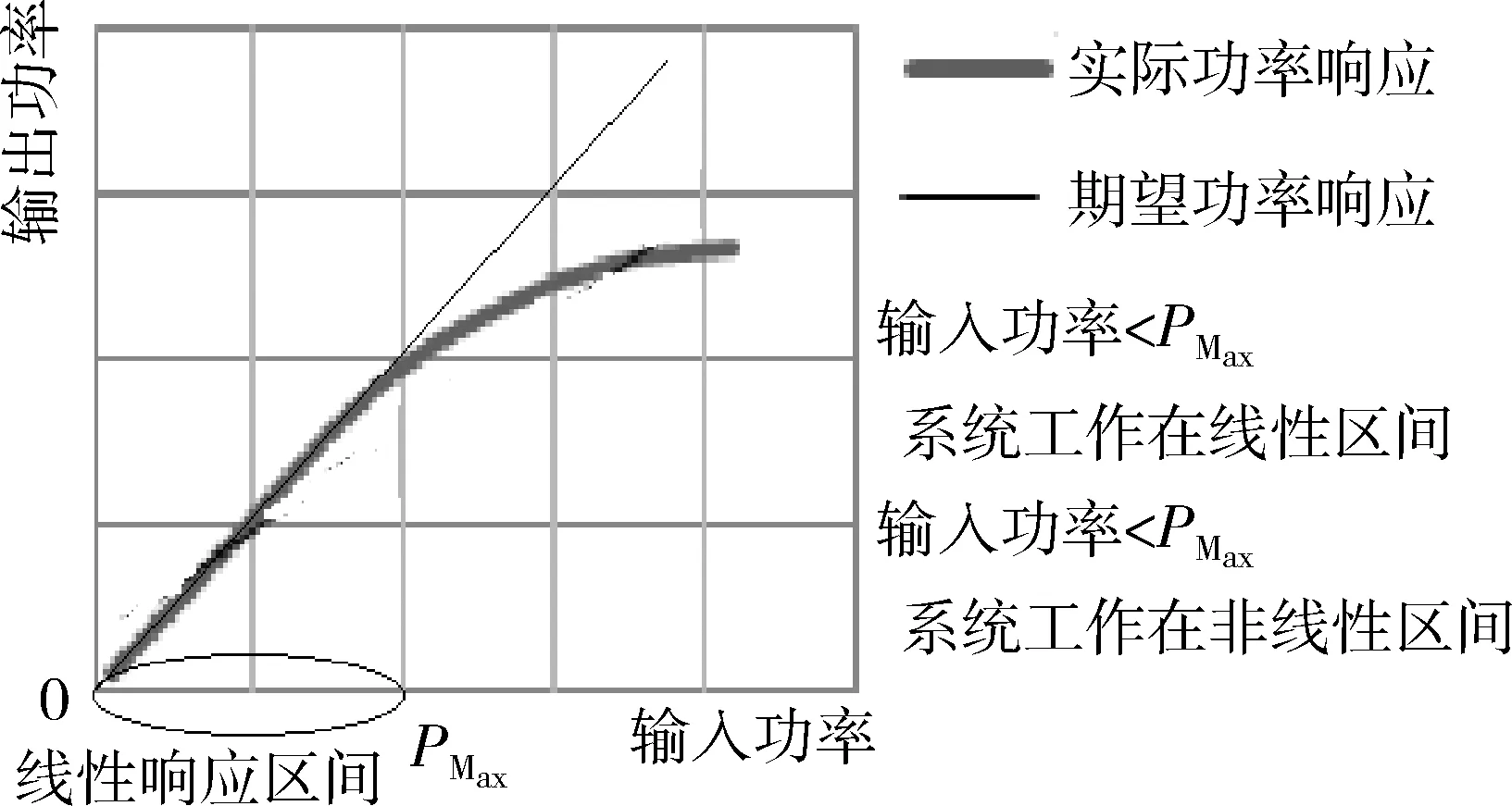
图1 功率放大器的输入输出特征

为了通过软件实现天线放大器的线性化并防止发射信号峰值被削波，定义了一个新的计算参数AMAPR：

(1)

在一般情况下，OFDM的PMAPR信号定义为：

(2)

(3)

波峰因数为：

(4)

2 应用PMAPR到OFDM系统

为了保证放大器工作在线性范围内， 利用信号峰值与天线放大器功率比，对输入放大器的信号x(t)进行加权处理。

2.1 发射端的实现步骤

附加了峰值处理模块的OFDM发送模型如图2所示。

发射端实现具体步骤如下：

(1)对x(t)设定帧的长度为N，例如设定0.5 s为一帧;

(2)找出每一帧的信号峰值：

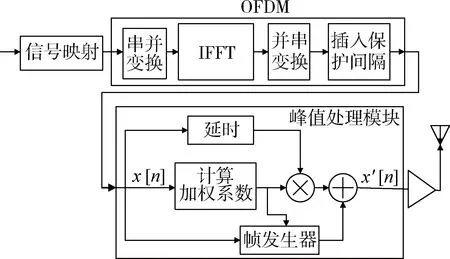
图2 附加了峰值处理模块的OFDM发送模型

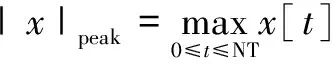
(5)

(3)根据式(4)计算帧加权系数；

(4)用帧发生器构造新的帧，帧包头包含帧起始识别码和帧加权系数；

(5)计算帧序列x’[n] :

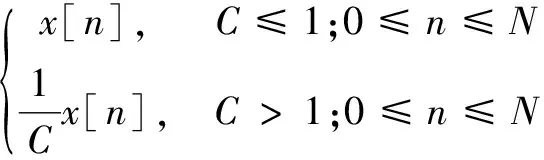
(6)

其中：N为帧的长度。

2.2 接收端的实现步骤

附加了峰值处理模块的OFDM接收模型如图3所示。

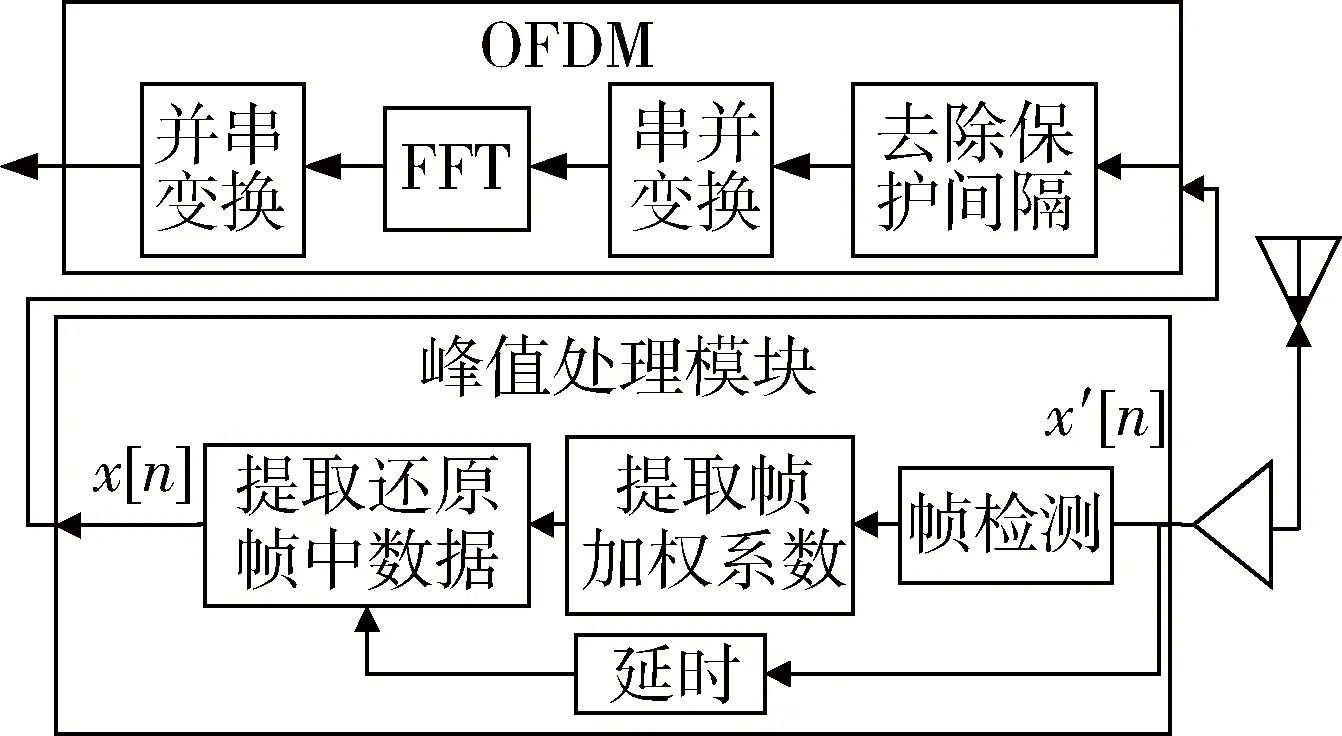
图3 附加了峰值处理模块的OFDM接收模型

接收端具体实现步骤如下：

(1)用帧起始识别码找到帧包头和帧加权系数C;

(2)利用帧加权系数还原帧参数：

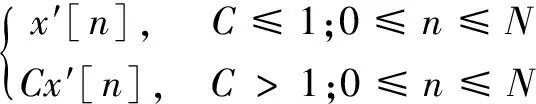
(7)

(3)利用常规OFDM计算还原信号。

3 实验仿真

3.1 仿真实验一

本系统通过仿真软件实现OFDM, 加入非线性函数仿真非线性放大器，如图4所示。

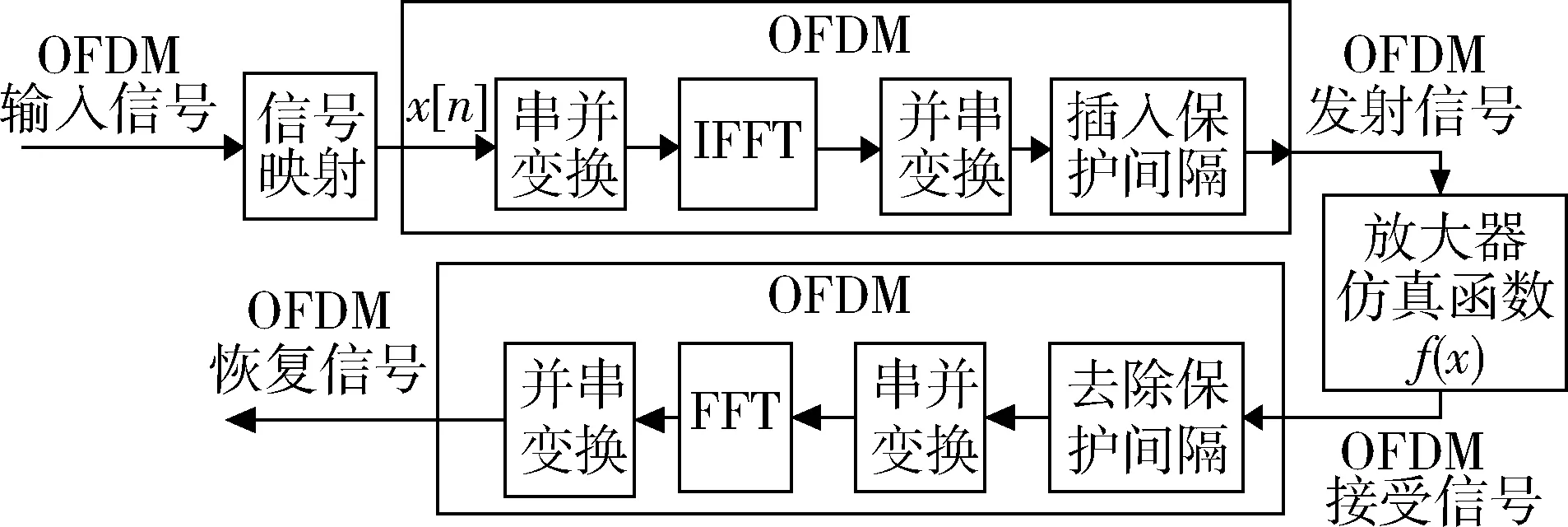
图4 含非线性功率放大器的OFDM系统

图4中放大器削峰仿真函数f(x)为：

(8)

伪真结果如图5所示。

图5 带非线性放大器语音仿真结果

3.2 仿真实验二

本系统在仿真实验一基础上，加入峰值处理模块如图6所示。仿真结果如图7所示。

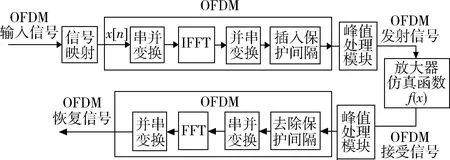
图6 含峰值处理模块和非线性功率放大器的的OFDM系统

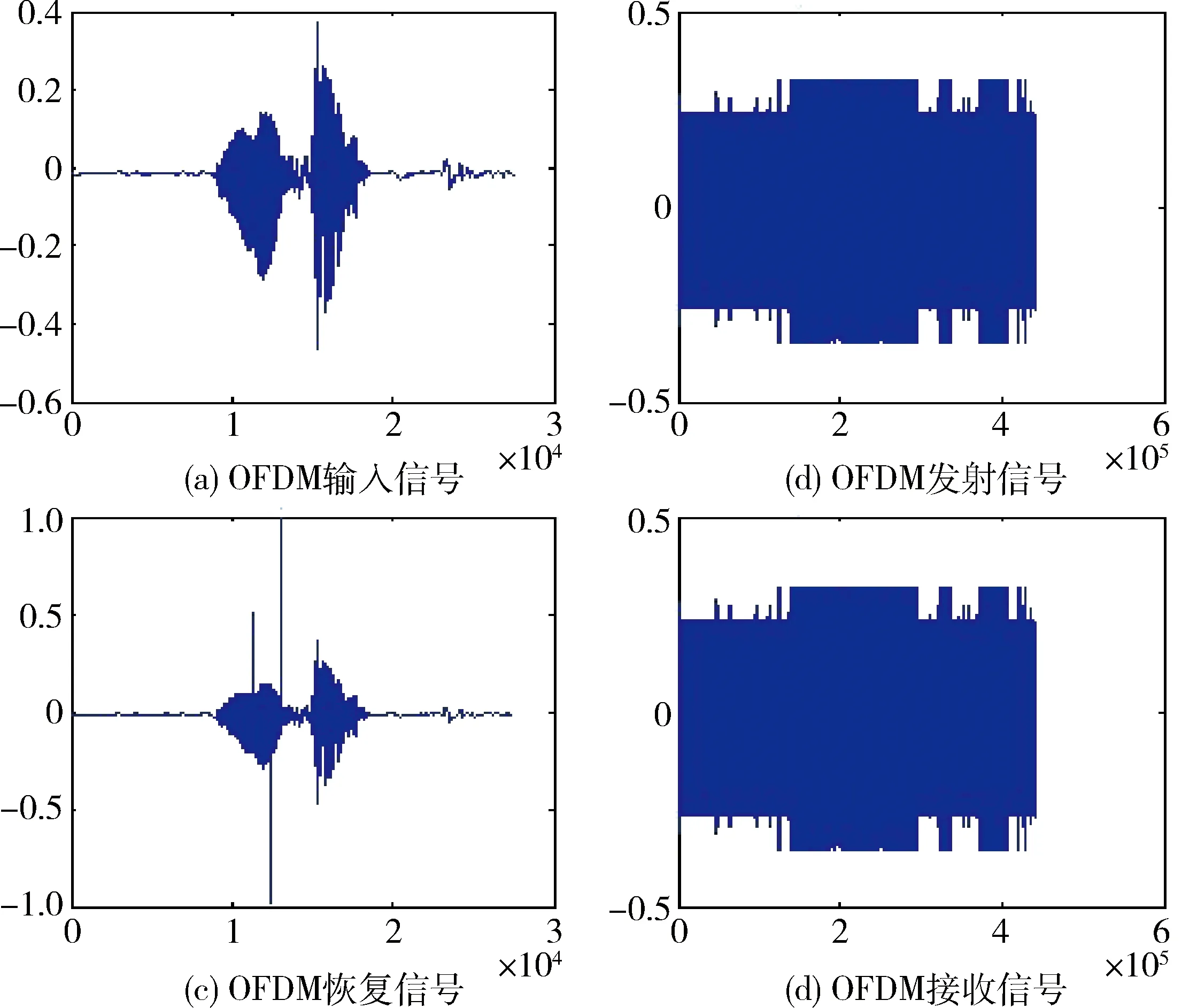
图7 加入峰值处理模块语音仿真结果

3.3 实验结果分析

在仿真实验一中，OFDM输入信号经过IFFT变换后，到达放大器输入端。由于放大器削峰仿真函数的作用，OFDM接收端与OFDM发射端相比，峰值被裁剪，从而导致OFDM恢复信号大幅失真，本实验的误码率高达27.35%。

在仿真实验二中，在放大器前后加入了基于PMAPR的帧加权技术，放大器的输入峰值信号被重新加权计算，以便输入信号中含有峰值的帧落入放大器的线性范围，而其他没有超出放大器线性范围的信号依然保持不变，这样有效地提高了信号的信噪比。经过帧加权处理过的信号，经过放大器削峰仿真函数的作用，恢复后的OFDM信号误码率仅仅为1.58%，大大提高了OFDM的抗失真性能。

3.4 算法的FPGA实现

通过FPGA可以实现本算法的高速运行。FPGA芯片根据时钟信号对数据流进行二级串转并变换，在数据流中找到帧头信号，利用程序中状态机对帧头进行检测、捕捉、校验，并根据编码原则对数据进行解码[9]，能够在FPGA芯片上有效地实现本算法的高速运行。

如果再结合软加权映射的局部聚类向量表示方法[10]，能提高编解码的识别率。

4 结论

通过对比仿真实验中的OFDM恢复信号, 进一步证明了AMAPR的加权算法能很好地防止数据射频发送失真。本文所提出的加权计算方法，有效地实现了 OFDM放大器的线性化处理，避免了峰值削波，降低了放大器成本，实现了天线的小型化。本文提出的AMAPR加权算法，对其他领域的放大器非线性补偿设计也有很好的参考价值。

[1] 罗涛.空时编码理论及其在OFDM移动通信系统中应用的研究[D].北京：北京邮电大学，2002.

[2] 罗涛，乐光新.多载波宽带无线通信技术[M].北京:北京邮电大学出版社，2004.

[3] WONG K T, WANG B， CHEN J C. OFDM PAPR reduction by switching null subcarriers & data-subcarriers[J]. Electronics Letters, 2011，47(1)：62-63.

[4] THOMPSON S C. Constant envelope OFDM phase modulation[C]. Military Communications Conference, 2005, 2:1129-1135.

[5] MULLER S H， HUBER J B. OFDM with reduced peak-to-average power ratio by optimum combination of partial transmit sequences[J].Electronic Letters, 1997,33:368-369.

[6] WUNDER G, BOCHE H. Upper bounds on the statistical distribution of the crestfactor in OFDM transmission[C]. IEEE Transactions on Information Theory, 2003,49:488-494.

[7] MULLER S H, BAUML R W, FISHER R F H, et al. OFDM with reduced peak-to-average power ratio by multiple signal representation[J]. Annals of Telecommunication,1997,52(1):58-67.

[8] Li Xiaodong, CIMINI L J. Effects of clipping and filtering on the performance of OFDM[J]. IEEE Communications Letters, 1998,2(5):131-133.

[9] 陈一波, 杨玉华, 王红亮, 等.高速数据采集与光纤传输系统的设计与实现[J].电子技术应用，2016，42(10)：73-76.

[10] 刘琦，梁鹏，周毅书，等.基于软加权映射的局部聚类向量表示方法[J].微型机与应用，2016，35(1)：38-41.

Using AMAPR frame weighting method to achieve linear output for power of OFDM antenna amplifier

Fan Xiaojing1， Zhang Shen2

(1. Engineer Training Center, Hefei University of Technology, Hefei 230601， China;2.Huawei Technologies Co., Ltd., Najing 210012, China)

The number of subcarriers for OFDM system causes large dynamic signal range and a very high PAPR (peak-to-average power ratio), which often causes nonlinear distortion of antenna amplifier and peak clipping and increases the bit error rate of the system. A more advanced algorithm for this issue is to use the peak factor PAR (peak-to-average ratio) as weight to reduce the PAPR, but the algorithm makes the input signal significantly attenuated, the signal to noise ratio decreased rapidly, and bit error rate increased. Based on the above problems, a new algorithm is proposed that is to use AMAPR (peak signal and antenna amplifier maximum ratio) to calculate weight of each frame. Only when the max power of input signal is greater than a maximum frame of power amplifier of the linear interval, then the linear compensation method is realized frame by frame. Calculation of the weighted coefficient will improve the signal to noise ratio as much as possible. Through simulation, the AMAPR frame weighting algorithm is proved that it can prevent peak clipping, improve the BER performance, and prevent signal attenuation. The new algorithm realizes the low cost antenna amplifier linear compensation.

AMAPR; OFDM; linear compensation; peak clipping

TP84;TN802

A

10.19358/j.issn.1674- 7720.2017.08.019

范晓晶，张珅.防止OFDM天线放大器峰值削波的AMAPR帧加权方法[J].微型机与应用，2017,36(8)：60-62，66.

2016-11-16)

范晓晶(1964-)，女，本科，高级工程师，主要研究方向：数控机床，计算机仿真。

张珅(1989-)，男，本科，项目经理，主要研究方向：通信软件管理。

________________________