核电厂地震概率安全评价中的电气设备易损度计算

宋 济，齐索妮，姚立珊

(中国核电工程有限公司电气仪控所，北京100840)



核电厂地震概率安全评价中的电气设备易损度计算

宋 济，齐索妮，姚立珊

(中国核电工程有限公司电气仪控所，北京100840)

随着福岛事故的发生，核电厂外部事件概率安全评价工作的重要性被各国核安全当局所认同。而地震，作为核电厂最为主要的外部事件，其对应的概率安全评价工作便更为人们所重视。易损度计算是完成地震概率安全评价的关键技术环节，其结果将被使用作概率安全评价事故序列模型的输入条件。因此，易损度计算的准确性和正确性对地震概率安全评价工作最终结论的影响也就不言而喻了。本文首先总体性介绍了设备易损度计算的基础数学模型，随后详细描述了核电厂地震概率安全评价中电气设备易损度计算的操作步骤，并重点探讨了电气设备功能失效模式下对试验反应谱和要求反应谱的处理简化技巧，最后通过具体算例阐述了电气设备易损度计算过程中的注意事项和简化技巧应用。

地震概率安全评价；易损度计算；反应谱削峰；电气设备

地震作为核电厂面临的最主要外部事件之一，对核电厂的安全评价有着重要贡献[1]。福岛事故的发生，印证了近些年在地质学领域发现的“核电厂厂址地区存在发生大于安全停堆地震(SSE)可能性”的研究结论[1]，即那些常认为不太可能发生的极端外部事件是会发生的[2]。我国核电厂在选址阶段仅进行外部事件的危险性评价，而未对外部事件的风险进行评价[2]。因此，在福岛事故后，国家核安全局对在建和运行核电厂提出了进行“福岛改进项”的指导性意见[1]。而在我国“十二五”核安全规划中，更明确提出了“2015年之前开展外部事件概率安全分析工作”的安排[2]。由此，核电厂外部事件概率安全评价正式成为了我国核电行业的“必修课”。

1 地震概率安全评价的数学模型

地震概率安全评价(SPSA)，作为现行地震风险评价的主要方法，与通用概率安全评价(PSA)方法相似，都是使用概率论的方法对核电厂风险进行评价。根据地震事件的特殊性，SPSA主要有3个关键技术环节：地震危险性分析、地震易损度评价、地震电厂响应分析。本文讨论的地震易损度评价的主要工作任务是得到重要构筑物和设备的易损度，即在给定地震参数，通常为厂址峰值地面加速度(PGA)，下的条件失效概率[2]。以上这3个SPSA关键环节在实际工作开展中存在若干交叉点，并不是直接按顺序依次实施的。SPSA的简化工作流程图在图1中提供，但此图并不能给出不同工作内容间的制约条件和严谨的逻辑层次，仅作为一个综述性的流程介绍，帮助读者概念性地了解SPSA的整体工作范围。

在SPSA的模型中，设备的抗震能力是一个随机变量，可完全由概率分布来描述。而在进行评估过程中，概率分布的形式以及设备的失效模式等都存在不确定性。在确定了失效模式和抗震能力的描述参数后，对应的概率分布可以得到一条对应的易损度曲线。因此，使用易损度曲线族就可以描述出易损度的不确定性，同时赋予每条曲线一个主观权重值来反映对每条易损度曲线的信任度。对于任意给定加速度，设备对应的易损度值(即条件失效概率)在0到1的范围内变化，其不确定性则由一个主观概率分布来体现。通过对累积主观概率对应易损度的寻找，研究人员便可绘制出置信度为高值(95%)、中值和低值(5%)的易损度曲线族，并完整表达出设备的抗震能力及相关不确定性，如图2所示。其中，在高值置信度曲线上5%条件失效概率对应的易损度值，被称为“高置信度低概率失效”(HCLPF)能力。对应图2中曲线族，可知HCLPF抗震能力值等于0.32 g。

应用图2中所示的易损度曲线，首先需要明确定义设备的失效模式。对于某一特定失效模式，可使用易损度曲线族的抗震能力中值Am和分别表示随机不确定性和认知不确定性的随机变量er和eu(中值为1)的最佳估计来表示。即抗震能力：

A=Am×er×eu

(1)

上式中，假定er和eu服从对数标准偏差为βr和βu的对数正态分布。于是，根据计算公式(1)及对数正态分布的假设，便可开发出对应的设备易损度曲线族，从而体现出其不确定性。

图1 地震概率安全评价简化工作流程[3]Fig.1 SPSA simplified workflow[3]

图2 易损度曲线族示例[3]Fig.2 An example ofthe family of fragility curves[3]

2 电气设备易损度计算总体流程

进行电气设备易损度计算的首要任务是定义设备的失效模式，对于有多种失效模式的情况，还应针对特定失效模式分别开发易损度曲线。如果存在明显的支配性薄弱环节，则仅用考虑此环节引发的失效模式。对于电气设备，通常会存在的失效模式包括：锚固失效(如支撑件弯曲变形、地脚螺栓松脱)、结构完整性失效(如柜体外壳变形)和功能失效(阀门卡死、旋转部件过量偏离、配电盘失电)。此外，断路器跳闸或继电器震颤情况还应进行单独考虑。

在确定了设备的失效模式后，易损度可使用中间随机变量代表的安全因子FE来表示设备高于设计要求的安全停堆地震ASSE的抗震能力。

FE=FEC×FRE×FRS

(2)

根据式(2)，则抗震能力中值：

Am=FE×ASSE=FEC×FRE×FRS×ASSE

(3)

式(3)中，FEC定义为设备能力因子，为使设备预期功能失效的加速度等级与抗震设计加速度等级的比值；FRE定义为设备响应因子，为设计阶段计算的设备响应与真实设备响应的比值；FRS定义为结构响应因子，是基于设备支撑位置处构筑物的响应特性得出的。

对于以上3个因子，在计算过程中都会伴随有2类不确定因子βr和βu。本质上，βr代表相同峰值加速度的地震特性和与其相关构筑物响应参数的随机性导致的不确定性；而βu代表的是以下原因造成的不确定性：

• 对构筑物材料真实特性的不确定，如强度、非弹性能量吸收、阻尼；

• 对构筑物模型计算结果与实际响应情况偏差的不确定；

• 使用工程经验或专家判断代替完整设计数据进行分析所带来偏差的不确定。

于是，对于抗震能力中值Am，与其相关的不确定因子:

(4)

(5)

值得一提的是，在抗震裕度评价(SMA)中，通过HCLPF值衡量设备的抗震能力，并使用置信度加权时条件失效概率来考虑相关随机性和不确定性。例如，本文图2中的HCLPF值为0.32 g，其含义是：在给定的地面加速度等级下，能有95%高置信度认为设备仅有极小概率(小于5%的可能性)失效的加速度值为0.32 g。而此值与易损度计算抗震能力中值的对应关系为：

HCLPF=Am×e-1.65(βr+βu)

(6)

在进行设备易损度计算时，通常也会利用公式(6)将HCLPF值一并计算出来，并与设备的设计抗震能力进行对照。如果两值相近(理想情况是HCLPF值大于设备设计抗震能力值)，则从侧面验证了给出易损度计算结果伴随不确定因子的置信度。

也有一些应用认为采用堆芯损坏的点估计值(均值)是足够保守的，不需要不确定性分析。在进行评估时，使用复合易损度曲线将随机性和不确定性整合为单一曲线。于是，复合易损度曲线由抗震能力中值Am和组合不确定因子βC两个参数定义。且：

HCLPF=Am×e-2.33·βc

(7)

公式(7)中的HCLPF值对应复合易损度曲线可以近似认为是1%条件失效概率(低于均值的-2.33对数标准偏差)的设备会失效加速度值[4]。此确定论失效裕度(CDFM)方法，相比于本文介绍的变量分离(SOV)方法，对于功能性和结构完整性极限抗震能力的评价是基于包络地震反应谱而不是中值地震反应谱，结果更加保守，计算过程更加简单(简化了对不确定因子的考虑)。详细信息可参见EPRI NP-6041-SL(参考文献[4])，本文不再展开讨论。

3 功能失效模式下的反应谱处理

3.1 反应谱处理的背景和目的

根据实际工程经验和对美国电力研究院(EPRI)SPSA专家的咨询结论，对于电气设备(特别是装有易震颤元件的电气柜)来说，除非存在现场安装操作未严格执行图纸规定或设备锚固方式有严重设计缺陷的情况，否则支配性失效模式通常为功能失效(如某类设备的安装锚固设计与传统方式有较大差异，应交由力学专业进行具体计算评估其失效方式的重要性)。因此，对电气设备功能失效模式下的易损度分析是整个评估工作的核心环节。

通常来说，电气设备抗震能力主要是通过地震台试验的方式进行鉴定的。如果在抗震试验期间，设备执行功能正常(即设备通过鉴定)，则抗震试验所使用的试验反应谱(TRS)和设备抗震设计的要求反应谱(RRS)便可用于设备地震易损度的评估。其整体思路是将TRS和RRS在关注频率范围内对比，找出设备在整个频域内的最薄弱点对应的比例因子(scale factor)(TRS/RRS)min，并使用此极限值推导出设备能力因子FEC，并结合设备响应因子FRE和结构响应因子FRS进行设备易损度的概率估算[5]。然而，大量研究分析表明，设备的功能失效不仅取决于反应谱的峰值加速度，更取决于整个反应谱曲线的均方根(RMS)值[4、5]；且反应谱曲线的RMS值对曲线上离散峰值不敏感。因此，窄频域内反应谱的峰/谷值对谱本身的RMS值没有显著贡献，不进行处理便会误导对设备能力因子极值对应频率的识别。此外，窄频谱与宽频谱在设备损坏方式和继电器震颤方面也有着不同的效果：宽频反应谱易引发多种失效模式及非线性振动反应间的相互作用。这也是通常情况下抗震鉴定TRS采用宽频谱的原因。

于是，如果TRS或RRS是窄频谱(RRS是窄频谱的情况比较多)，则必须先对其进行“削峰”，即将窄频谱转化为宽频谱的处理。削峰处理的基本流程在3.2节中进行简述，更详细的原理和工作步骤可参见EPRI TR-103959 第3章“Response Spectra Clipping Factors”的描述[5]，本文不再累述。

3.2 削峰处理的基本流程

本节使用仅包含一个峰值的反应谱(如 图3-1 所示)为例，提供了削峰处理的常规流程如下(对于包含多个峰值的反应谱，可重复进行以下步骤)[4、5]。

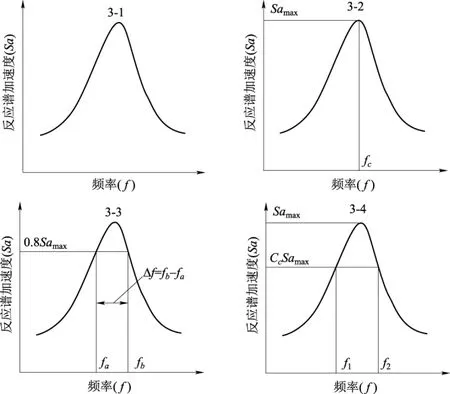
图3 削峰常规流程示意图Fig.3 Illustration of clipping routine procedure

1) 确定反应谱的峰值加速度Samax和对应频率fc(如图3-2所示)；

2) 画一条对应0.8Samax的横轴平行线，得到与反应谱交点的对应频率fa、fb；

3) 计算峰值频带宽度Δf0.8，参数B(如 图3-3 所示)，其中

Δf0.8=fb-fa

(8)

B=Δf0.8/fc

(9)

4) 计算削峰因数(clipping factor)Cc，其中

(10)

5) 计算此削峰因数的不确定因子βu，其中

(11)

6) 使用削峰因数确定新的峰值 (CcSamax) 和对应起止频率范围[f1,f2] (如图3-4所示)；

3.3 削峰的实用简化技巧

核电厂内安全级电气设备数量众多，潜在削峰处理工作量巨大，因此尽可能灵活地使用简化处理技巧对提高电气设备功能失效模式下的易损度计算效率十分有效和必要。

3.3.1 总体原则

在得到设备的TRS和RRS时，可以原则性地先从以下2个方面着手，有效减少后续的计算工作量：

(1) 确认关注频率范围。

根据EPRI SPSA专家给出的建议，一般情况下，对于电气设备，如果其一阶固有频率小于10 Hz，频率关注范围取一阶固有频率到 50 Hz；如果一阶固有频率大于10 Hz，则取10～50 Hz。因此对于此频率范围外的反应谱峰值可以不进行削峰处理。

(2) 同时考虑TRS和RRS的谱形。对于确定不会推导出(TRS/RRS)min的反应谱峰值不进行削峰处理。因为反应谱削峰的目的是为了得到更准确的比例因子，即(TRS/RRS)min。因此，进行削峰计算前，若通过观察可直观判断(TRS/RRS)min不可能在TRS或RRS的某一峰值处得到(例如TRS峰值频率处对应RRS的斜率大于0)，则不再对此峰值进行削峰处理。

(3) 根据实际经验，对于没有明显窄频峰值的RRS可直接看做是宽频谱而不进行削峰处理。

3.3.2 简化处理正确性验证

以下给出的原则用于检验拟定的简化方案是否得当：

(1) 对于谱形复杂的反应谱，可简化的处理方法并不唯一；但对于无法直观判定哪个峰值最可能得到(TRS/RRS)min的情况，不能轻易省略削峰。

(2) 如果在计算之前通过判断，省略了对反应谱上某个峰值的处理。那么，在计算得到水平和竖直方向上的(TRS/RRS)min后，应返回检查此(TRS/RRS)min的对应频率是否属于原反应谱中未处理峰值的削峰频率区域内([f1,f2])。

(3) 对反应谱曲线上任意点，只能进行一次削峰处理。通常，对于拥有多个峰值的反应谱都会进行多次削峰，但是应注意原谱中任意频率值最多只能被包含在削峰处理频率范围(图3中f1-f2范围)内一次。

反应谱削峰处理是一项需要经验积累，灵活处理的技巧性工作，没有严格的准则和规定用于直接遵照或参考。因此，SPSA电气工程师除了要及时总结日常工作中的经验外，更要重视同行之间的交流探讨。

4 电气设备易损度计算实例

在本节，本文选用国内某核电厂实际采购的6.6 kV中压开关柜设备为例，使用EPRI TR-103959中给出的方法[5]进行易损度计算。通过此算例，对电气设备易损度计算方法的实际应用进行阐述，并对过程中的注意事项、实用简化处理和不确定因子的经验选取进行讨论。

4.1 背景信息介绍

本次易损度算例中，地震局通过历史地震数据，使用5组地面运动时程曲线取均值得到核电厂厂址10-4(次/年)超越概率、5%构筑物典型阻尼比下，一致概率危害度反应谱(UHRS)对应安全停堆地震ASSE的水平地面加速度峰值(PGA)为0.174 g。设备的抗震能力评估将以此值为基准进行评估。

SPSA结构专业考虑了3组构筑物模型参数来表现其实际结构自振频率的不确定性：最佳估计(BE)、下限(LB)和上限(UB)。同时，模拟了3组(BE、LB和UB)不同土壤条件。通过排列组合，形成以下5个最终分析模型组合：

• BE结构模型+BE土壤条件；

• BE结构模型+LB土壤条件；

• BE结构模型+UB土壤条件；

• LB结构模型+BE土壤条件；

• UB结构模型+BE土壤条件。

最后针对以上每个组合，均使用地震局提供的5组地面运动时程曲线(共25组)取均值，生成了包括5%阻尼比下的对应厂房不同楼层的水平方向地震反应谱；竖直方向的曲线直接使用对应水平方向曲线乘以2/3的系数生成。对于厂房构筑物的建模，此处使用3维集总质量杆模型。

6.6 kV中压开关柜设备安装在电气厂房+7.00 m层的电气间中，且同排相邻电气柜体间通过螺栓进行相互固定。不同类型、尺寸的电气开关柜(断路器柜、PT柜、F-C柜、母联进线柜等)已经按照现场实际布置情况，在地震台整体成排进行过抗震鉴定，并得出设备的一阶固有频率分别为20.2 Hz(柜体前后方向)，13.51 Hz(柜体左右方向)和35 Hz(竖直方向)[6]。此处值得注意是：对于柜内安装有继电器的电气柜，如果现场走访时发现同排相邻柜体间未有锚固措施而导致存在相互作用，则根据抗震试验(柜体间有锚固)数据计算出的设备易损度值将无法有效评估继电器震颤情况。

4.2 确定失效模式

4.2.1 失效模式的种类

对于电气设备主要考虑的3种失效模式：锚固失效、结构完整性失效和功能失效。根据本例中电气开关柜的抗震鉴定报告，试验结束后被鉴定设备未出现结构外观变形、破损情况，且功能性完好[6]，由此可断定结构完整性失效不是设备的支配性薄弱环节。根据电气开关柜供货商提供的锚固安装图纸[7]和设备外形图图纸[8]中的信息(结构、质量、底板锚固方式等)，可以断定锚固失效也不是设备的支配性薄弱环节。因此，对于本例中的电气开关柜设备，需要集中考虑的是功能失效模式，即支配性薄弱环节。

4.2.2 继电器震颤在失效模式中的分析原则

继电器震颤作为电气设备功能失效的重要诱因，需在装有继电器(包括拥有触点)的设备上进行分析。继电器震颤分析在SPSA模型主要分三种情况考虑：

(1) 对经过二次回路分析，认定即使发生震颤也不会产生造成不良后果的动作命令的情况，即识别为“非关键继电器”。则在PSA模型中由继电器控制的设备如按功能失效考虑，应使用继电器所在设备的 “事故后”易损度值。

(2) 对经过二次回路分析，认定继电器触点震颤会导致预期安全功能无法实现，且无法对电路的“保持(seal-in)”或“闭锁(block)”状态进行复位的情况，即识别为“关键继电器”。则在PSA模型中由继电器控制的设备如按功能失效考虑，应使用继电器所在设备的“事故期间”易损度值。

(3) 对经过二次回路分析，对发生继电器震颤后可以通过复位使设备安全功能执行能力得到恢复的情况，则PSA模型中由继电器控制的设备如按功能失效考虑，应使用继电器所在设备的“事故期间”易损度值，但还应叠加对人因失效的考虑，以降低设备的失效概率。在进行人因分析时需考虑有无报警或其他仪表指示信息，及同时产生的报警信号或指示信息的数量、有无操作规程指引、执行动作时间窗口和可达路径等因素。

由上可知，SPSA中继电器震颤分析的关注范围包括：继电器元件抗震能力(由继电器所在设备的“事故期间”易损度代表)、继电器的初始位置、震颤后果、对应驱动的0层设备、0层设备期望状态、报警指示信息和复位手段等。本算例中，相关开关柜未识别出“关键继电器”。

4.3 功能失效模式下的易损度计算

4.3.1 关注频率范围的选取

对于基于抗震试验鉴定的电气设备，计算其易损度抗震能力时涉及鉴定试验反应谱与抗震设计要求反应谱(安装楼层处)的比较，因此首先要确定反应谱中关注的频率范围。根据设备的抗震鉴定试验报告，电气开关柜的一阶固有频率约为13.5 Hz[6]，因此本次计算的频率关注范围取10～50 Hz。

4.3.2FEC及对应βu_C、βr_C计算

通过观察，初步认定电气柜的要求反应谱(+7.00 m处楼层反应谱)和抗震试验反应谱均不是典型宽频谱(见图4)，需要进行削峰处理。

图4 +7.00 m处楼层反应谱(FRS)Fig.4 Floor response spectrum (FRS) at +7.00 m

首先对FRS进行处理，E-W方向的FRS谱分别对应频率9.04 Hz和23.7 Hz处存在峰值，依照EPRI TR-103959[5]中公式3-39至3-44进行削峰。此处给出最大峰值(9.04 Hz处)的处理过程：

加速度峰值Sapk_EW=1.20g,=>0.8Sapk_EW=0.96g。

在原反应谱中找出对应0.8Sapk_EW的频率分别为：7.25 Hz和10.24 Hz，fc_EW=9.04 Hz已知。于是：

Δf0.8_EW=10.24-7.25=2.99 Hz，

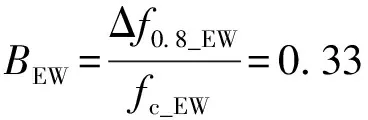
∴Cc_EW=0.58。

SacpkEW=CcEW·SapkEW=0.70g。

在原反应谱中找出加速度0.70 g对应的频率分别为5.99 Hz和11.42 Hz。于是将原反应谱[5.99 Hz，11.42 Hz]频率区间内对应加速度更新为0.70 g。

对原反应谱23.7 Hz处峰值也进行相同的处理，Sacpk2EW=0.40g,削峰频率区间为[16.96 Hz，30.79 Hz]。同样的，对N-S、竖直方向的FRS进行削峰处理，经过削峰后的FRS见图5。

TRS的处理方法与FRS完全一致，这里不再累述。

接下来使用已经处理过的FRS、TRS计算比例因子。将三个方向上的TRSclipped/FRSclipped分别进行对比，得到以下结果[5]：

fcritical=24.16 Hz。

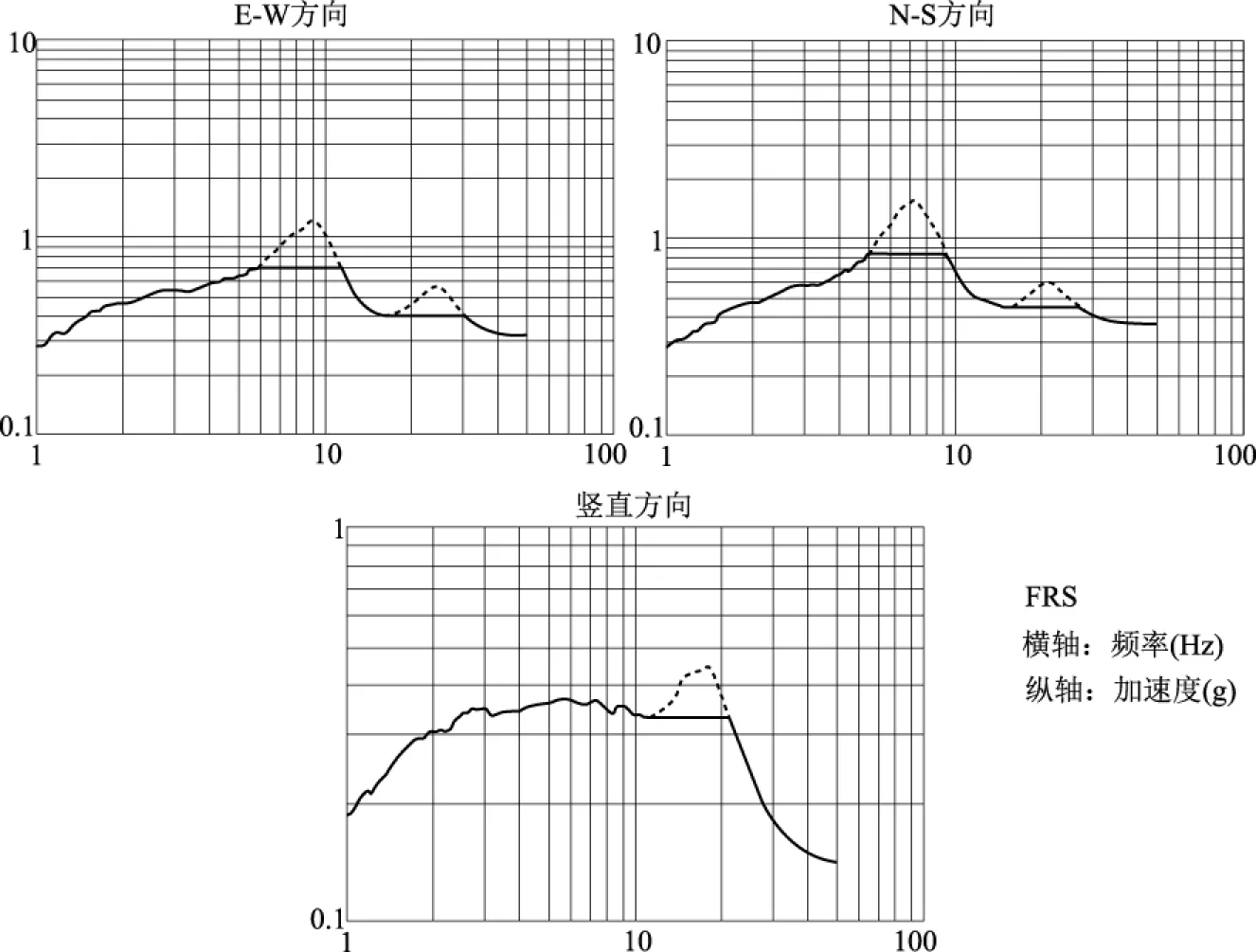
图5 削峰处理过后的楼层反应谱(FRS)Fig.5 Floor response spectrum (FRS) after clipping

在此处应注意的是，应根据设备的布置图纸确认水平方向上TRS与FRS的对应关系。本算例中，柜体左右方向的TRS对应东西方向的FRS；柜体前后方向的TRS对应南北方向的FRS。因为在fcritical不属于FRS或TRS的削峰频率范围内，因此此处FRS和TRS的裁剪因子均为1,不确定因子为0，即

FCc_FRS=FCc_TRS=1；

βuCc_FRS=βuCc_TRS=0。

若fcritical属于削峰范围，则裁剪因子为Cc_x/y/z,不确定因子使用公式(11)求得[5]。

根据EPRI TR-103959[5]3-65页的描述，保守地选取设备能力放大因子CI=1.1，不确定βuci=0.05βuCi=0.05。

根据EPRI TR-103959[5]中表3-14的信息，对于进行抗震鉴定试验，且试验后功能完好的设备，宽频输入谱设备能力因子FD_dur=1.4,βu_D_dur=0.22,βr_D_dur=0.09(事故期间);FD_aft=1.95,βu_D_aft=0.28,βr_D_aft=0.09(事故后)。

不确定因子：

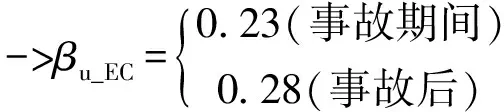
βr_EC-βr_D-0.09(事故期间、事故后)

4.3.3 计算设备响应因子FRE及相关不确定因子βu_RE、βr_RE

如上节所述，FCc_FRS=1；βuCc_FRS=0。

根据EPRI TR-103959[5]3～66页的描述，如果FRS是由单个时程曲线推导得出的话，则除了地面处的设备以外，其他安装在上面楼层的设备都应使用要求降低因子DR(0.92)进行修正，以补偿要求谱的非普遍性[5]，其对应不确定因子βu_Dr=0.04。但如果FRS是由多个时程曲线推导得出的，则无需进行修正[5]。如4.1节所述，本算例FRS由25组曲线取均值得出，因此DR=1，βu_Dr=0。

4.3.4 计算结构响应因子FRS及相关不确定因子βu_RS、βr_RS

结构响应因子及相关不确定因子的计算的主要涉及方面如表1所示。

表1 结构响应参数汇总

此部分的评估工作一般由结构专业建模时统一进行，电气专业仅需提取使用即可。在本算例中，根据结构专业提资，结构响应因子：

FRS=∏Fm=1.09，

不确定因子：

4.3.5 计算设备抗震能力中值加速度(Am)及相关不确定因子βr、βu

本算例中，参考PGA为0.174g(4.1节)，因此设备抗震能力中值：

Am_dur=FEC_dur·FRE·FRS·PGAref

=0.55g(事故期间)，

Am_aft=FEC_aft·FRE·FRS·PGAref

=0.77g(事故后)。

对应不确定因子：

=0.43(事故期间),

=0.46(事故后),

=0.27。

同时，HCLPF值也在一并计算：

HCLPFdur=Am_dur·e[-1.65·(βudur+βr)]

=0.17g(事故期间),

HCLPFaft=Am_aft·e[-1.65·(βuaft+βr)]

=0.23g(事故后)。

值得指出的是：虽然此处为单类电气设备计算出两类抗震能力加速度中值Am(事故期间和事故后)，但并不表示同一类设备针对不同时期(事故期间和事故后)具备两个不同的抗震能力(功能失效模式下)。而应根据4.2.2节介绍的继电器震颤分析的三种情况，选取一个使用到SPSA模型中。对于不包含可能震颤元件(继电器、低压接触器触点等)的电气设备，应直接使用“事故后”Am值。

另一个需要强调的概念是在SPSA模型中，真正作为输入条件，代表设备地震易损度的是抗震能力加速度中值，即Am，而不是高置信度低概率失效加速度值，即HCLPF。此处HCLPF的计算，仅是为了与相关设备原始抗震能力设计值比较，定性地作为设备易损度评估有效性的参考依据。而HCLPF的计算结果与设备鉴定试验的设定裕度、试验报告提供信息的充分度、易损度评估的整体不确定因子等因素都有直接关系，因此设备HCLPF与抗震设计值的定量比较并没有绝对指导性。如本例中，电气柜的抗震设计加速度为0.2g，而由于鉴定试验中TRS相较于FRS裕度过小，导致易损度评估中计算出的事故期间HCLPF值仅为0.17g，但并不等于此设备为不合格产品。若使用较为保守确定论失效裕度法(CDFM)的公式(7)进行计算，则HCLPF值可有一定提高。(参见第2节)

5 结语

关于SPSA，国外的研究方法已较为成熟，且在多个核电厂的地震风险评估中进行了实际应用[2]。而在国内还处于起步阶段，主要通过外委咨询、自我消化吸收、同行评定交流的方法在逐步培养人才、增强团队执行能力，以便尽快迎头赶上，达到国际先进水平。通过本文的介绍，也可发现SPSA是一项需要多专业、多领域协同配合，交流互助才能完成好的复杂工作。因此，作为电气工程师及设计人员，除了充分掌握与本专业相关的工作内容外，也应该纵向了解结构专业、力学专业甚至核电厂安全概率分析模型的工作概况，才能更加系统地理解本专业工作内容的意义和在整个SPSA工作中的位置。如此，我国才能尽快培养出具有扎实理论背景，过硬执行能力的SPSA工作团队，早日跻身国际先进水平，为我国核工业在未来数十年的蓬勃发展提供坚实后盾和安全保障。

[1] 卢放，闫林，三环路核电厂的抗震裕度评价. 核科学与工程, 第35卷第2期, 2015年6月.

[2] 付陟玮，张东辉等，核电厂地震易损性分析模型研究. 原子能科学技术,第47卷第10期, 2013年10月.

[3] Seismic probabilistic risk assessment implementation guide, EPRI 2013 Technical report 3002000709. California: EPRI, 2013.

[4] A methodology for assessment of nuclear power plant seismic margin, EPRI NP-6041-SL [R]. California: EPRI, 1991.

[5] Methodology for developing seismic fragilities, EPRI TR 103959 [R]. California: EPRI, 1994.

[6] UniGearZS1/ZVC型中压开关柜样机抗震鉴定试验报告, 国核安发[2005]109号. 中国核动力研究设计院, 核级设备鉴定中心, 2010年.

[7] 地基开孔图，第2、3页，图纸编号：CJX52210101360A44DD, A版. ABB，2010年.

[8] 地基开孔图，第1页，图纸编号：CJX52210101360A44DD, A版. ABB，2010年.

The Fragility Computation of Electric Equipment in Nuclear Power Plant’s Seismic Probabilistic Safety Assessment

SONG Ji, QI Suo-ni, YAO Li-shan

(China Nuclear Power Engineering Co., Ltd., Beijing 100840, China)

With the occurrence of Fukushima nuclear accident, the necessity of external events probabilistic safety assessment (PSA) for nuclear power plants is gradually recognized by nuclear safety administrations in various countries. Moreover, earthquake, as the original responsible cause of Fukushima nuclear accident, is identified as one of the most important external events which deserve special attention from the PSA’s perspective. The fragility computation, the calculated results of which would be used as input subjects for PSA accident sequence model, is one indispensable step to accomplish the seismic probabilistic safety assessment (SPSA). Based on this fact, the accuracy and validity of fragility calculation contribute a significant impact to the final conclusion of SPSA. In this paper, the fundamental mathematic theory of equipment fragility computation is briefly introduced at first, and then the general procedure of fragility calculation for electrical equipment is given with test response spectrum and required response spectrum clipping techniques in functional failure mode specially discussed in the following sections. In the last part of this paper, one explicit fragility computation example of electrical switchgear is offered, with the purpose of revealing some matters needing special attention and useful finesses to facilitate the calculation during the computation.

SPSA; fragility calculation; Response spectra clipping; Electric equipment

2016-11-17

宋 济(1984—)，男，湖北武汉人，工程师，硕士研究生，主要从事核电厂电气系统的设计审查工作

TL364+.5

A

0258-0918(2017)02-0276-11