基于调度运行数据的稳定极限分析
周 悦,蔡 田,卢子敬
(1.国网湖北省电力公司,湖北 武汉 430077;2.国网黄冈供电公司,湖北 黄冈 438000)
0 引言
对于电网安全运行,最具有指导意义的参照物就是离线稳定极限,它由系统方式专业人员根据相关规定制定,同时以相对更直观、更可控的有功功率来表示,但稳定极限的制定过程中往往会预留一定的裕度[1],以保证稳定极限能够适应各种电网运行方式,即目前电网的稳定极限可以以极高的概率保证“稳定”,但往往并非实际的“极限”。
随着电力市场化的推进,新能源电厂的大量接入,使得在部分时段内,水电新能源基地的外送能力被稳定极限限制,因此若能对稳定极限的裕度进行合理的评估,在保证安全的前提下充分发挥线路的外送能力,对于充分消纳清洁能源、降低碳排放有着非常重要的意义。
湖北宜昌地区近两年由于产业调整,本地用电负荷降低,而根据原负荷规划而配套建设的大量水电厂在集中来水的情况下,需要外送的电力远超外送断面的输送能力,此外,新能源电厂的接入也进一步加重了外送压力。针对宜昌外送断面之一的“220 kV远双+坡掇”断面,本文以28个月的电网实际运行数据为基础,对运行极限进行分析,对离线稳定断面的裕度进行评估。
1 偏差来源
对于离线稳定极限的计算过程,计算误差的主要来源如下:
(1)模型偏差:由于离线计算建模的问题,导致计算线路参数与实际不符,进而造成稳定计算结论出现偏差。模型偏差只能通过实际运行进行很粗略的校验,只有出现对应线路的计划检修或者跳闸时才能检验稳定断面的适用性,同时还必须排除其他线路的停运以及SCADA的测量误差引起的偏差。
(2)转换偏差:稳定规定给出的控制对象是有功功率,而热稳定的控制对象是电流,虽然两者之间在220 kV以上输电网中存在很高的线性性[2],但转换边界条件的设置仍会造成相当可观的误差。以《2017年华中主网稳定规定(第二版)》为例,在500 kV线路的控制有功和控制电流的转换上,电压取500 kV,功率因素取0.95,而在实际的电网运行中500 kV母线电压通常都在525 kV到540 kV之间,即使出现N-1或者同杆N-2故障,也不会出现电压大幅下降的情况,同样的,对于输送有功功率在300 MW以上的500 kV线路来讲,其功率因素往往都在0.98以上,此时引起的偏差至少在5%以上,当控制条件更加苛刻时[3-4],所引起的误差显然会进一步增大。
(3)不确定因素偏差[5]:对于同样的稳定断面运行功率,由于断面包含线路的功率分配不同,其故障后的功率分布肯定会存在一定的不同,在某些极端情况下甚至可能出现相同的断面功率,不同的稳定结论。因此由于在离线计算中难以穷尽各种可能的运行方式,因此方式人员往往在最后确定断面极限时留有一定的裕度,然而具体的裕度大小却难以有统一标准。
2 分析方法
在文献[6]中证明了对于给定支路k(两端节点编号为m和n)和j(两端节点编号为p和q),断开支路k后,其电流将以一个恒定的比例a转移至支路j,具体公式为:

其中:为节点导纳矩阵;Zj为支路j的阻抗。
需要指出的是式(1)中转移比a为一个矢量,为便于分析,后续分析中所指的转移比均指a的模量。
为验证上述结论,取相同的电网接线方式下(近区全接线运行)的多个时刻在线DSA计算数据,分别进行远双线(安全电流515 A)、坡掇线(安全电流710 A)的N-1计算。
其中选择宜昌及近区电网全接线方式的时段,以避免由于近区网络结构破坏造成的转移比偏差;对于不同开机、不同负荷水平、不同无功设备投退情况下对于电压、无功的影响,则采取对多个时间点多次抽样分析的方法,其计算结果如表1所示。

表1 远双线、坡掇线相互之间的转移比Table 1 The transfer ratio between AC line Yuanshang and Poduo
由表1可知,两条线之间转移比偏差在不同时刻差别很小,转移比最大值和最小值之差不超过1%,因此可以认为文献中提出的转移比恒定是在电网准确建模的前提下是可以精准确定故障后电流分布的。但是,计算数据的建模正确与否只能通过实际停电/跳闸检验,在进行分析的24个月的实际电网运行中,远双线、坡掇线各有3次停电,其中远双线的全部三次以及坡掇线的第三次停电时,近区电网都不是全接线运行,因此无分析意义。表2是坡掇线第一、第二次停送电时对远双线的转移比(SCADA数据采样周期300 s)。

表2 坡掇线停(送)电时,对远双线的转移比Tab.2 The transfer ratio to AC line Yuanshuang while AC line Poduo is on(off)
由于实测的转移比会因为采样间隔的问题(采样周期300 s),导致在相邻的采样周期中电网的发用电情况略有不同,而在在线DSA计算中,停电前后的发用电情况是完全一致。为消除采样周期过长的影响,在第一次坡掇线送电时,调整SCADA的采样周期至5 s,这时得到的坡掇线对远双线的转移比为16.2%。
3 误差分析
由以上分析可知,在通过缩短采样周期至5 s后,可以认为近区机组和负荷无变化,此时坡掇线对远双线的转移比为16.2%,在忽略装置测量误差的前提下,可以认为该值就是坡掇线对远双线的实际转移比。
3.1 模型偏差
由于潮流计算中都是采用的Π型等效电路(如图1所示,假设线路首末段分别为i和j),第二节中所指的线路电流对应图1中的iij,而表1中用于转移比计算的线路电流为图1中的i1,两者相差为ic(线路电容电流的一半),只有在忽略线路导纳时,才可以认为iij=i1;此外,考虑到母线电压的变化幅度很小,可认为ic为一个恒定值(对于坡掇线约为12 A的容性电流),因此当相关线路电流越大时,模型引起的偏差会越小。故即使计算模型和参数完全一致,由于线路首端电流(i1)与支路电流(iij)存在略微的差别,造成在不同的时刻计算得到的转移比略有不同。
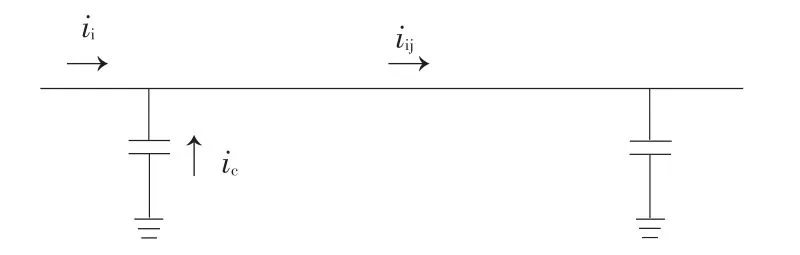
图1 线路Π型等效模型Fig.1 Type-Π equivalent model of AC line
由表1可知,不同时刻的转移比均值与时间转移比16.2%完全一致,虽然不同时刻之间的转移比略有不同,但只要线路电流能够远大于电容电流,这时由于模型引起的误差是可以忽略的。
3.2 转换偏差、不确定因素偏差
选取2014年9月至2016年12月,28个月中远双+坡掇断面有功在300 MW以上的运行采样点,共计12 199个(采样周期300 s)。由于这些时刻中,远双线、坡掇线的电流均远大于线路的电容电流,因此远双线对坡掇线转移比以及坡掇线对远双线转移比根据表1的计算结果分别取27.5%和16.2%。
通过转移比可以非常准确地推测出远双线、坡掇线任一线路跳闸后运行线路上的电流,若此时运行线路的电流超过线路规定安全电流,则认为此时断面是不安全的(图2、图3中红色部分)。

图2 稳定边界(按电流)Fig 2 Stable boundary(by current)
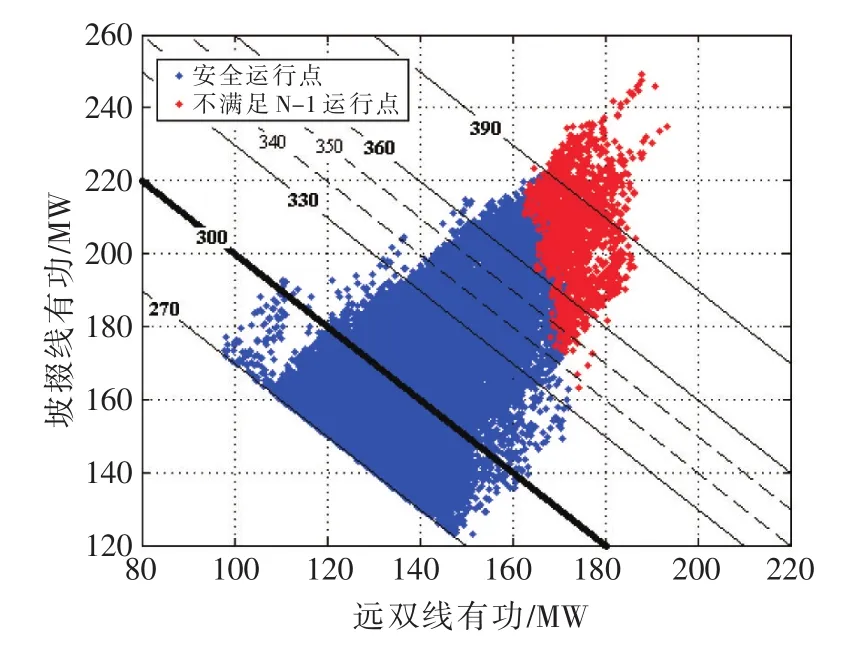
图3 稳定边界(按有功)Fig 3 Stable boundary(by active power)
4 断面裕度的评估
将图1中运行点的电流坐标改为对应运行点的有功坐标(如图2所示),由图2可知稳定规定中远双线、坡掇线的稳定极限300 MW可以保证所有运行点出现任一线路N-1后,运行线路均不过载,但显然在300 MW的稳定极限以上仍有相当一块区域是不存在N-1问题,这部分运行点占所有稳定极限300 MW以上运行点的85.1%(10385/12199),在所有的安全运行点中,断面功率最大值为387.155 MW,在所有不安全运行点中,断面功率最小值为337.636 MW,在断面功率不同时,安全/不安全运行点的分布表3所示。

表3 安全/不安全运行点的分布Tab.3 Distribution of safe/unsafe spot
定义断面功率为P时的不安全运行概率:

不安全运行点的频数分布以及断面不安全运行概率(ΔP=5 MW)的分布如图4、图5所示。
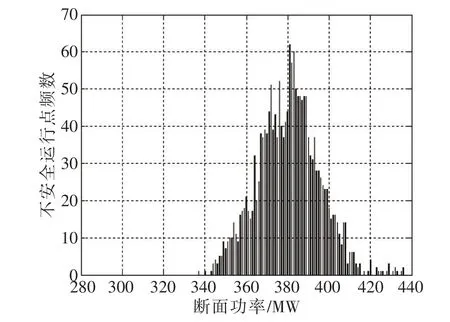
图4 不安全运行点的频数分布Fig 4 Frequency distribution of unsafe spot

图5 不安全运行概率Fi.g 5 Unsafe operation’s probability
由图4、图5可知,若将稳定极限P增加到332 MW,仍可保证p(P)=100%,原超稳定极限的12 199个运行点中4 457个运行点(占比36.49%)将被视为稳定极限以内的运行点,即可以在完全保证电网稳定,且留有一定裕度(ΔP=5 MW)的情况下,同时释放出相当的裕度。
5 结论
根据以上分析可知,对于近区电网结构相对稳定,且有充分运行经验积累的稳定断面,通过对长时间的运行数据进行分析,特别是结合线路检修或事故停电时的运行数据,可以得到非常精确的断面限值。对于本文中分析的稳定断面,经过24个月的运行数据以及数次断面组成线路停电前后的记录数据,精确地确定了该断面的运行极限,对照稳定规定要求,规定的断面稳定极限确实可以完全保证“稳定”,但距离“极限”仍有一定空间,而这一部分运行空间如能合理使用,则能够在该地区水电及新能源电厂大发时做到既保证电网安全又能最大程度消纳清洁能源。
[参考文献](References)
[1]中华人民共和国国家经济贸易委员会.DL755-2001电力系统安全稳定导则[S].北京:中国电力出版社,2001.The state economic and trade commission of the People's Republic of China.DL 755-2001 Guide on security and stability for power system[S].Beijing:China Electric Power Press,2001.
[2]王守相,武志峰,王成山.计及不确定性的电力系统直流潮流的区间算法[J].电力系统自动化,2007,(5):18-22.WANG Shouxiang,WU Zhifeng,WANG Chengshan.Interval algorithm of DC power flow considering uncertainty in power systems.Automation of Electric Power Systems[J].2007,(5):18-22.
[3]陈祎,郭瑞鹏,叶琳,等.电网断面热稳定限额计算模型及方法[J].电力系统自动化,2012,36(17):20-24.CHEN Yi,GUO Ruipeng,YE Lin,etal.Calculation model and method for thermal stability control limit to transmission interfaces in a power Grid[J].Automation of Electric Power Systems,2012,36(17):20-24.
[4]赵娟,申旭辉,吴丽华,等.结合直流潮流模型的电网断面热稳定极限快速评估方法[J].电力系统保护与控制,2015,43(03):97-101.ZHAO Juan,SHEN Xuhui,WU Lihua,et al.Fast evaluation method on thermal stability limit of power grid cross-section with DC power flow model[J].Power System Protection and Control,2015,43(03):97-101.
[5] Aleksandar Dimitrovski,Kevin Tomsovic.潮流建模中的不确定性—边界潮流法的应用(英文)[J].电力系统自动化,2005,(16):6-15.Aleksandar Dimitrovski,Kevin Tomsovic.Uncertainty in load flow modeling-application of the boundary load flow[J].Automation of Electric Power Systems,2005,(16):6-15.
[6]李淼,周悦.利用支路间转移比唯一性制定在线稳定断面适用性的研究[J].湖北电力,2014,38(02):9-11.LI Miao,ZHOU Yue.A study on the establishment of online stable sections by using constant transfer ratio between branches[J].Hubei Electric Power,2014,38(02):9-11.

