厦门市仙岳路多孔连续箱梁顶升关键技术研究
刘志翁 (广东大雄经济技术咨询有限公司,广东 广州 510075)
厦门市仙岳路多孔连续箱梁顶升关键技术研究
刘志翁
(广东大雄经济技术咨询有限公司,广东 广州 510075)
厦门市仙岳路改造为全程高架快速路工程施工中,为避免拆旧桥带来的负面社会影响,充分利用原桥结构,对部分桥梁顶升改造,该措施工期短、经济效益好。厦门市仙岳路上跨湖滨东路高架桥第一联为4×35 m预应力砼连续箱梁,该联上部结构总重8 000 t,顶升最大高度达3.6 m,顶升施工及监控难度大,需对各顶升关键技术进行详细分析才能保证工程的顺利进行。
顶升施工;弯箱梁;支反力;强迫位移;局部应力
1 箱梁顶升方案设计
厦门市仙岳路的快速化改造是将原有的湖滨东路口跨线桥、莲岳路口跨线桥、福厦路口跨线桥顶升与新建的桥梁连接,实现仙岳路全程高架,其中湖滨东路跨线桥的4×35 m预应力砼连续箱梁顶升为本次改造工程的难点。该箱梁为空间曲线箱梁,箱梁顶宽24.8 m,梁高2 m,梁重达8 000 t,湖滨东路跨线桥横断面见图1。由于顶升高度大,顶升过程长,施工前应制定详细的计划和对各关键问题充分论证方能确保顺利完成箱梁的顶升。
1.1 箱梁各墩台顶升步长控制
湖东路跨线桥第一联桥梁顶升布置见图2,各墩顶升高度及逐次顶升控制值详见表1。H0号台顶升高度最大为3 625 mm,因此以H0号台的顶升距离作为控制值,H0号台顶升最大步长为100 mm,全部顶升过程共分42步,全梁在顶升过程中均应保持为刚体运动。
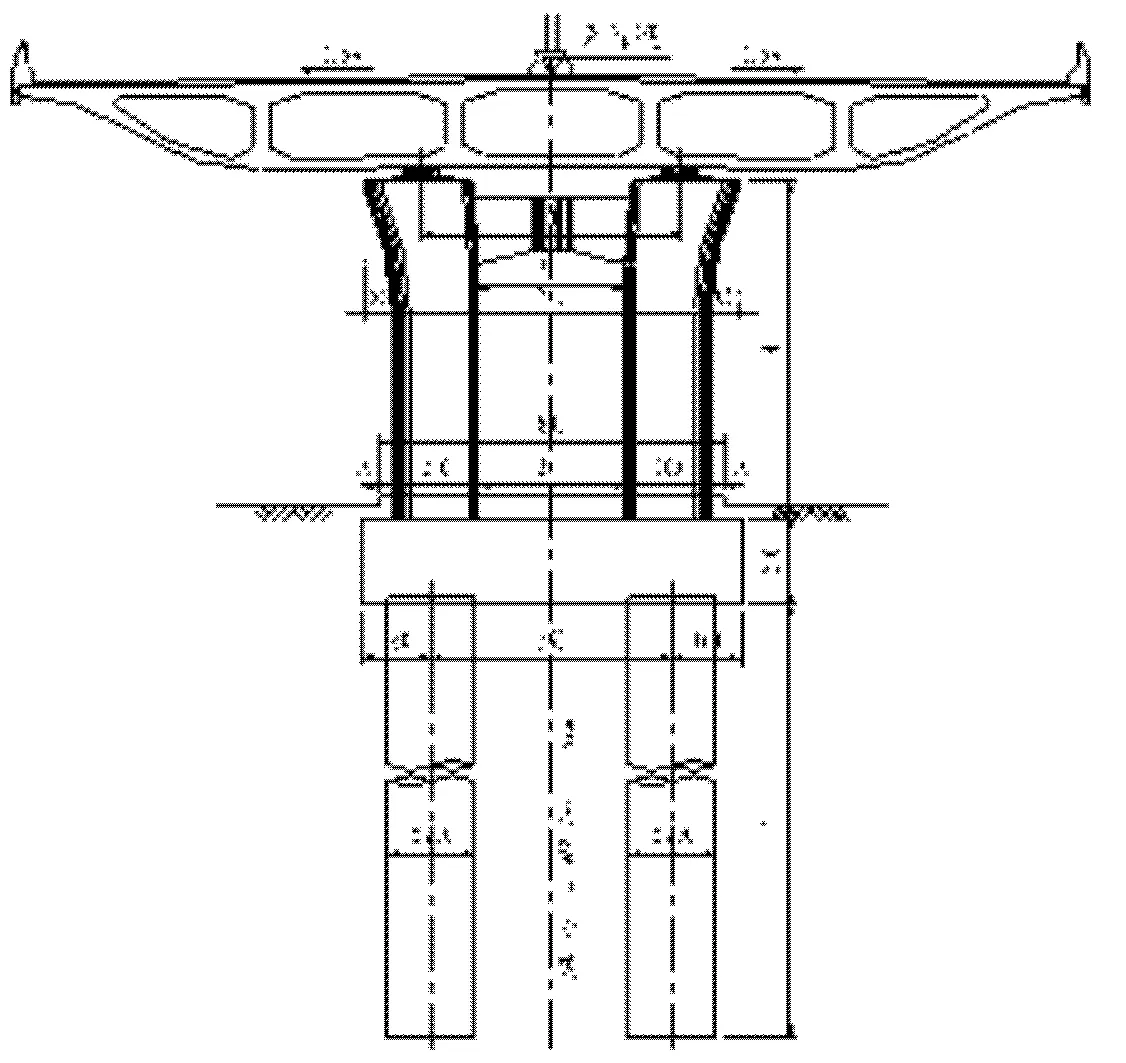
图1 湖滨东路跨线桥横断面图

图2 湖滨东路跨线桥第一联顶升布置图
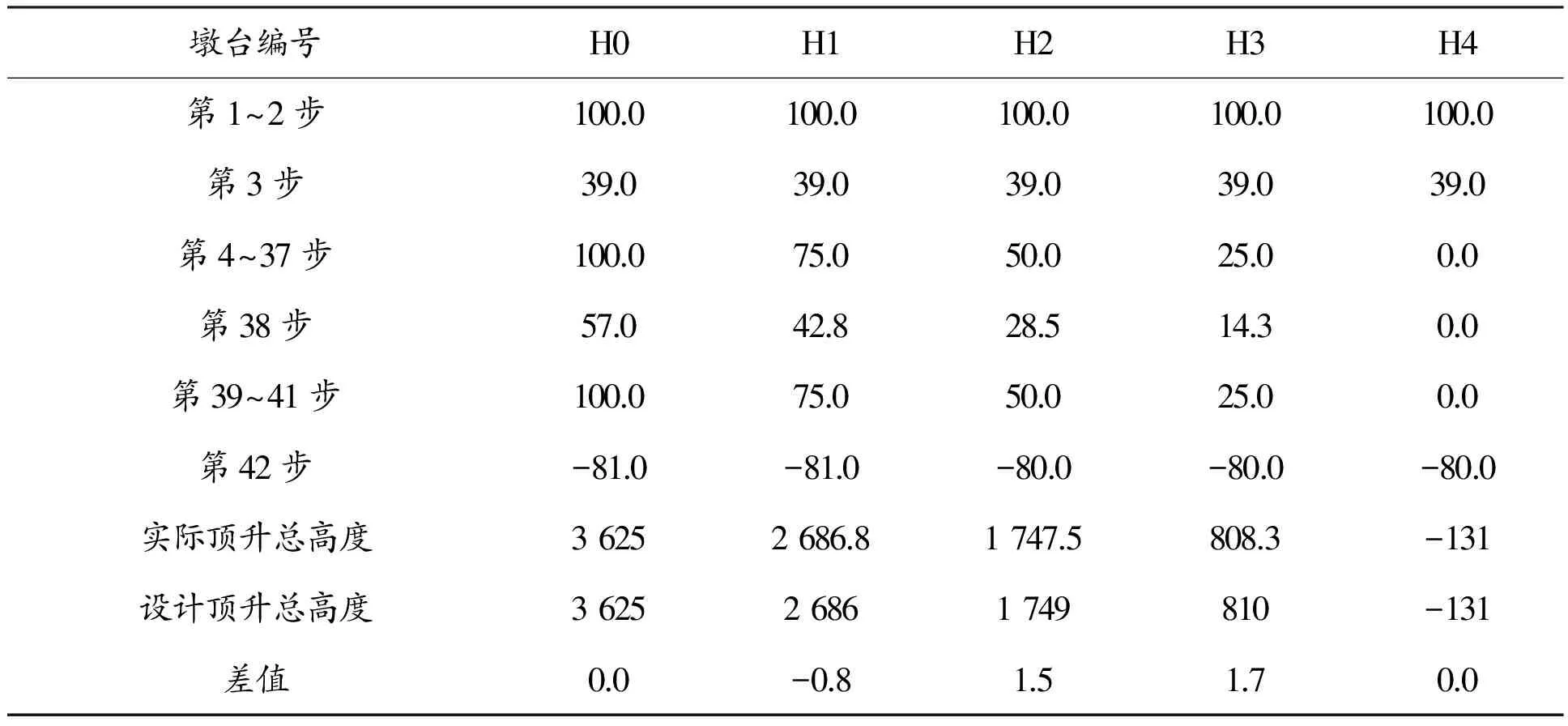
表1 各墩逐次顶升控制值 mm
1.2 梁底分配梁设计
为避免集中应力过大,在箱梁与千斤顶之间设置了分配梁,其中H0台及H4墩设置横向分配梁,横向分配梁由3根I36b工字钢组成,横向分配梁设置见图3。

图3 横向分配梁设置图
H1号墩、H2号墩及H3号墩采用纵向分配梁,纵向分配梁同样由3根I36b工字钢组成。
1.3 墩台顶临时支撑
千斤顶每升高100 mm后需要将千斤顶回油,将支撑钢管接高后进行下一步顶升,因此在千斤顶回油前需先将临时支撑接高,当千斤顶回油后箱梁就落到临时支撑上,这时将支撑钢管接高进行下一步的顶升。桥台临时支撑设在台帽上,桥墩临时支撑设置在原支座垫石处,临时支撑设置平面见图4。

图4 临时支撑设置平面图
2 顶点反力计算及千斤顶的选型
箱梁顶点反力计算采用通用有限元分析软件Midas进行计算,计算单元类型采用梁单元,采用只受压单元模拟千斤顶。H0号台千斤顶平面布置见图5,H1、H2及H3号墩千斤顶平面布置见图6,H4号墩千斤顶平面布置见图7。
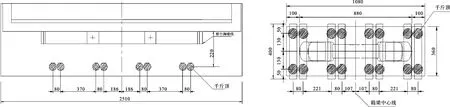
图5 H0号台千斤顶平面布置图 图6 H1、H2及H3号墩千斤顶平面布置图
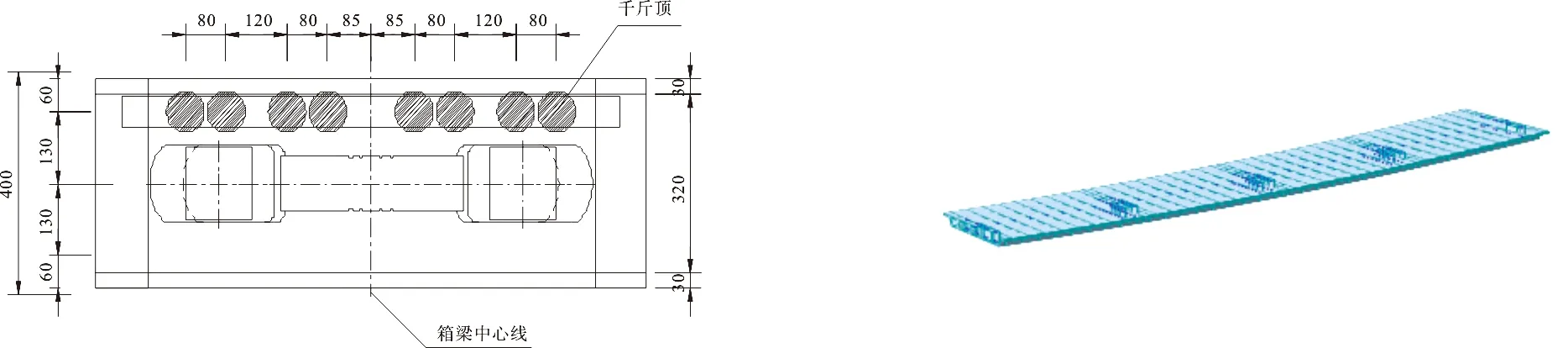
图7 H4号墩千斤顶平面布置图 图8 Midas计算模型
2.1 计算模型
箱梁共40个单元,虚拟横梁共64个单元,只受压单元64个,Midas模型见图8。由于顶升阶段主要考察的是各墩顶升高度不同步时箱梁产生的应力增量,故建立计算模型不对预应力束进行模拟。
2.2 顶升力计算结果
千斤顶的编号由内向外依次为1、2、…、8, 千斤顶平面布置及其编号见图9。由于顶升过程中不能保证每个千斤顶不出现故障,因此计算千斤顶的顶升力分5个工况,工况一:全部千斤顶均有效工作,工况二:H0号台的4号千斤顶失效;工况三:H1墩前排4号千斤顶失效;工况四:H1墩后排4号千斤顶失效;工况五:H2墩前排4号千斤顶失效。
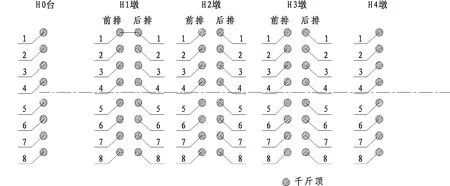
图9 千斤顶编号平面图
2.2.1 工况一
全部千斤顶均正常工作时,H0号台~H4号墩千斤顶反力见表2。
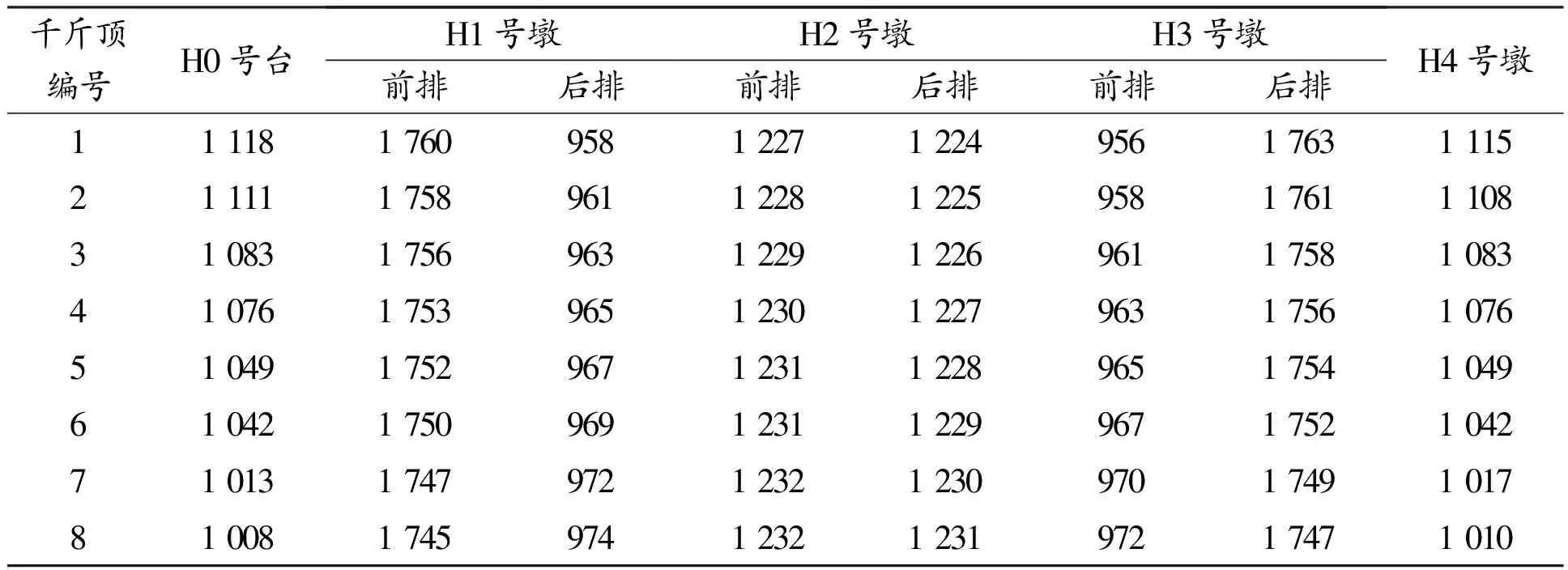
表2 H0号台~H4号墩千斤顶反力 kN
2.2.2 工况二
H0号台的4号千斤顶失效时的H0号台~H4号墩千斤顶反力见表3。
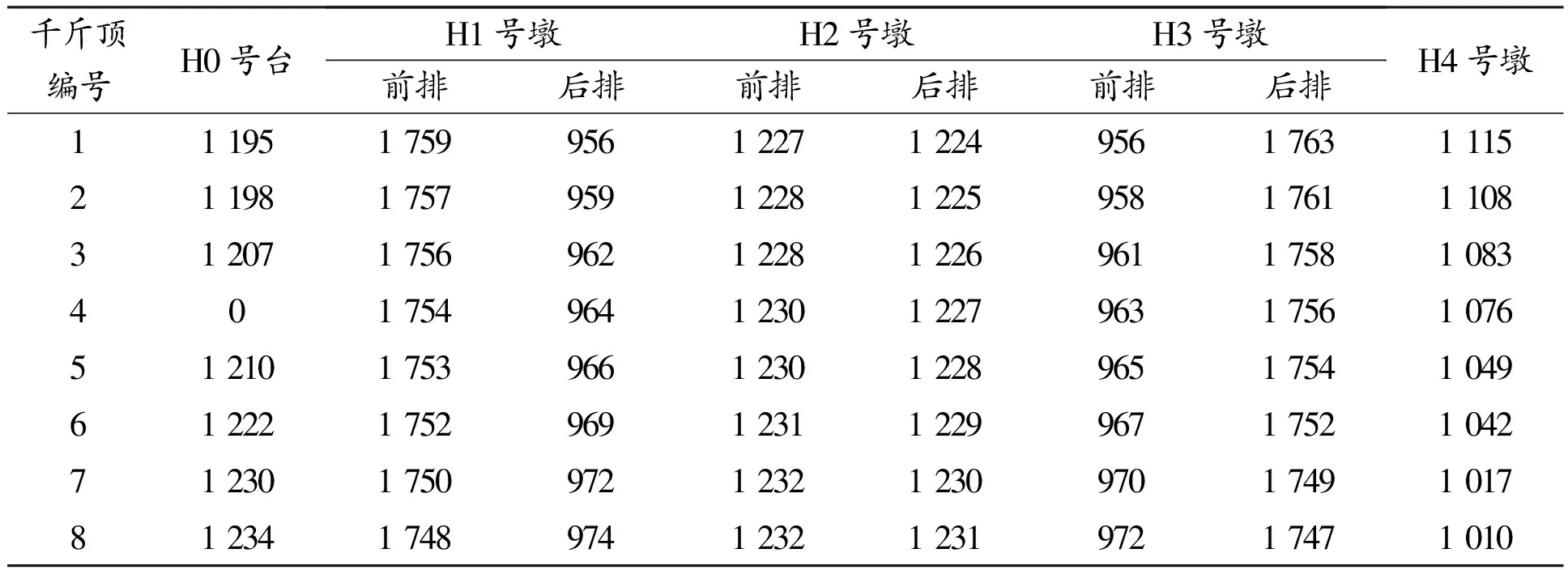
表3 H0号台~H4号墩千斤顶反力 kN
2.2.3 工况三
H1号墩前排的4号千斤顶失效时的H0号台~H4号墩千斤顶反力见表4。
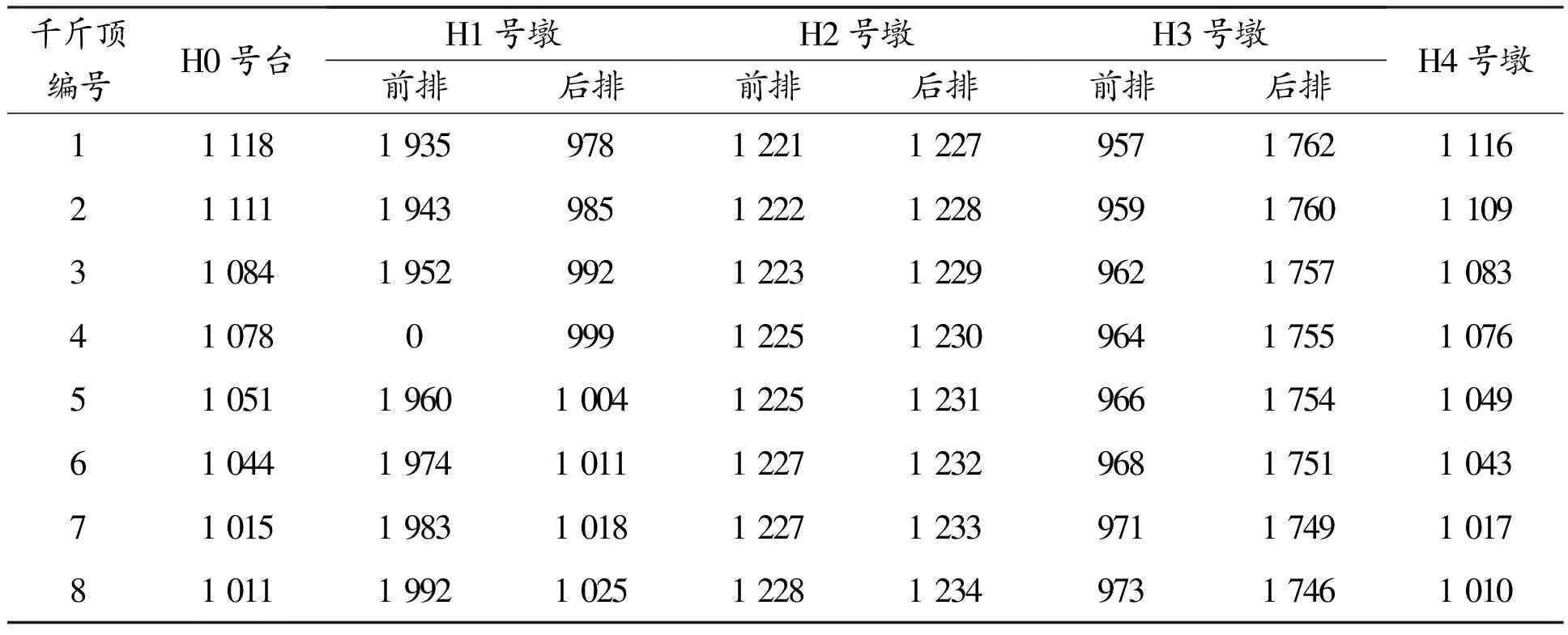
表4 H0号台~H4号墩千斤顶反力 kN
2.2.4 工况四
H1号墩后排的4号千斤顶失效时的H0号台~H4号墩千斤反力见表5。
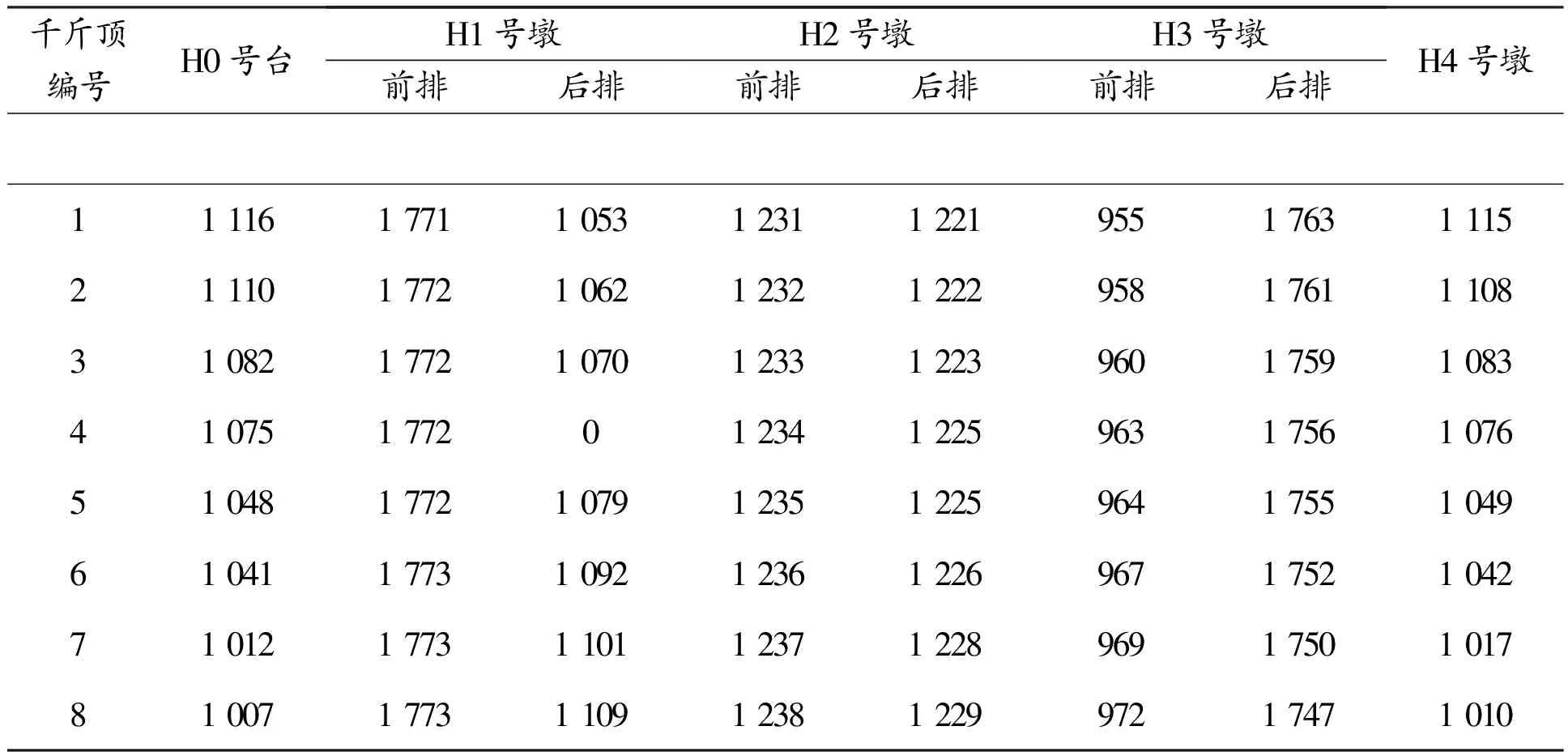
表5 H0号台~H4号墩千斤反力 kN
2.2.5 工况五
H2号墩前排的4号千斤顶失效时的H0号台~H4号墩千斤顶反力见表6。
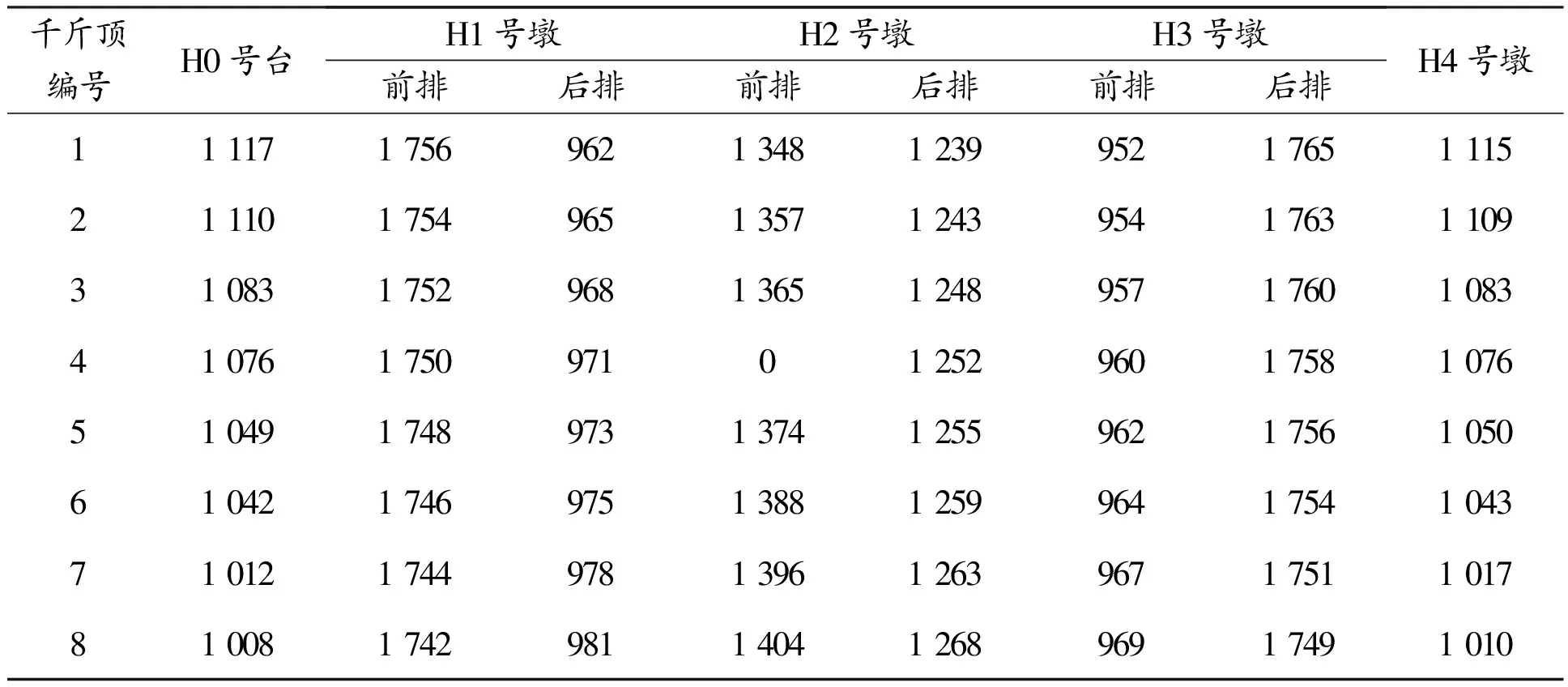
表6 H0号台~H4号墩千斤顶反力 kN
2.3 千斤顶的选型
由表2~表4可知:工况三的千斤顶最大反力为1 992 kN, 本项目采用200 t千斤顶其顶升力富余量基本没有,实际顶升施工过程中H1号墩与H3号墩的千斤顶多次出现故障,说明全部64个千斤顶均采用200 t的千斤顶不合理,应按理论计算结果合理选择千斤顶的型号。就本工程而言, H1号墩前排、H3号墩后排千斤顶应选用300 t的千斤顶,其余可采用200 t的千斤顶。
3 顶升过程中箱梁应力增量及扭转角的控制
3.1 箱梁纵向顶升不同步计算
箱梁同步顶升过程中,如遇顶升距离大,顶升子步骤多,顶升过程必然会出现各墩顶升量不完全同步的情况,此时顶升过程中梁体就不完全是刚体运动,梁内也就会因强迫位移的产生而出现附加应力。因此,首先要考察当梁内出现最大附加应力1.83 MPa(C50砼抗拉强度设计值)时各墩顶箱梁的最大强迫位移,按上述要求计算各墩顶箱梁的最大强迫位移。
工况一为H0台的最大强迫位移计算,由计算得知,当H0台强迫位移为-38 mm时H1墩梁顶出现的附加拉应力为1.82 MPa。工况二为H1墩的最大强迫位移计算,由计算得知,当H1墩强迫位移为-17 mm时H1墩梁底出现的附加拉应力为1.83 MPa。工况三为H2墩的最大强迫位移计算,由计算得知,当H2墩强迫位移为-15 mm时H2墩梁底出现的附加拉应力为1.81 MPa。
分析各计算结果可知:各墩台最大强迫位移按15 mm控制可避免箱梁产生的附加应力不超过C50砼的抗拉强度设计值1.83 MPa。因此,在顶升过程中,应将顶升最大步距100 mm再分成7个子步,分别为6个15 mm和1个10 mm的顶升子步,即每顶升15 mm应检查一次各墩顶箱梁有无出现强迫位移,如出现强迫位移或各墩顶箱梁的应力增量超过1.83 MPa,必须在消除强迫位移和降低应力增量后方可进行下一子步的顶升。
3.2 箱梁横向不同步产生扭转角的内力及应力计算
内外侧顶点不同步产生的高差按子步20 mm步距控制,内外侧顶点距离为9 760 mm,扭转角为arctan(20/9 760)=0.12°。当箱梁产生0.12°扭转角位移作用下,箱梁最大附加拉应力为1.76 MPa,满足规范要求。
通过箱梁纵向顶升不同步及横向不同步的计算分析可知,纵横向顶升不同步不能同时出现,否则箱梁拉应力可能超过规范要求,因此在施工监控中应严格控制箱梁的顶升速度,随时关注应变及位移的变化,确保箱梁顶升过程中不出现过大的拉应力,避免发生工程事故。
4 顶点处箱梁及支座垫石局部应力分析
原箱梁每个墩台设置两个支座,本次箱梁顶升的顶点个数均大于两个,墩台处顶升点均为8个,钢垫板均为60 cm×60 cm。临时支撑点为两个,桥台临时支撑为8个,桥墩临时支撑为两个,桥墩临时支撑设在原支座位置。由以上分析可知:临时支撑处的箱梁和支座局部应力最大,故仅验算上述两处局部应力,局部应力验算采用ANSYS软件计算。
4.1 临时支撑处箱梁局部应力分析
箱梁临时支撑处的最大反力为9 820 kN,楔形块尺寸大小为130 cm×130 cm。
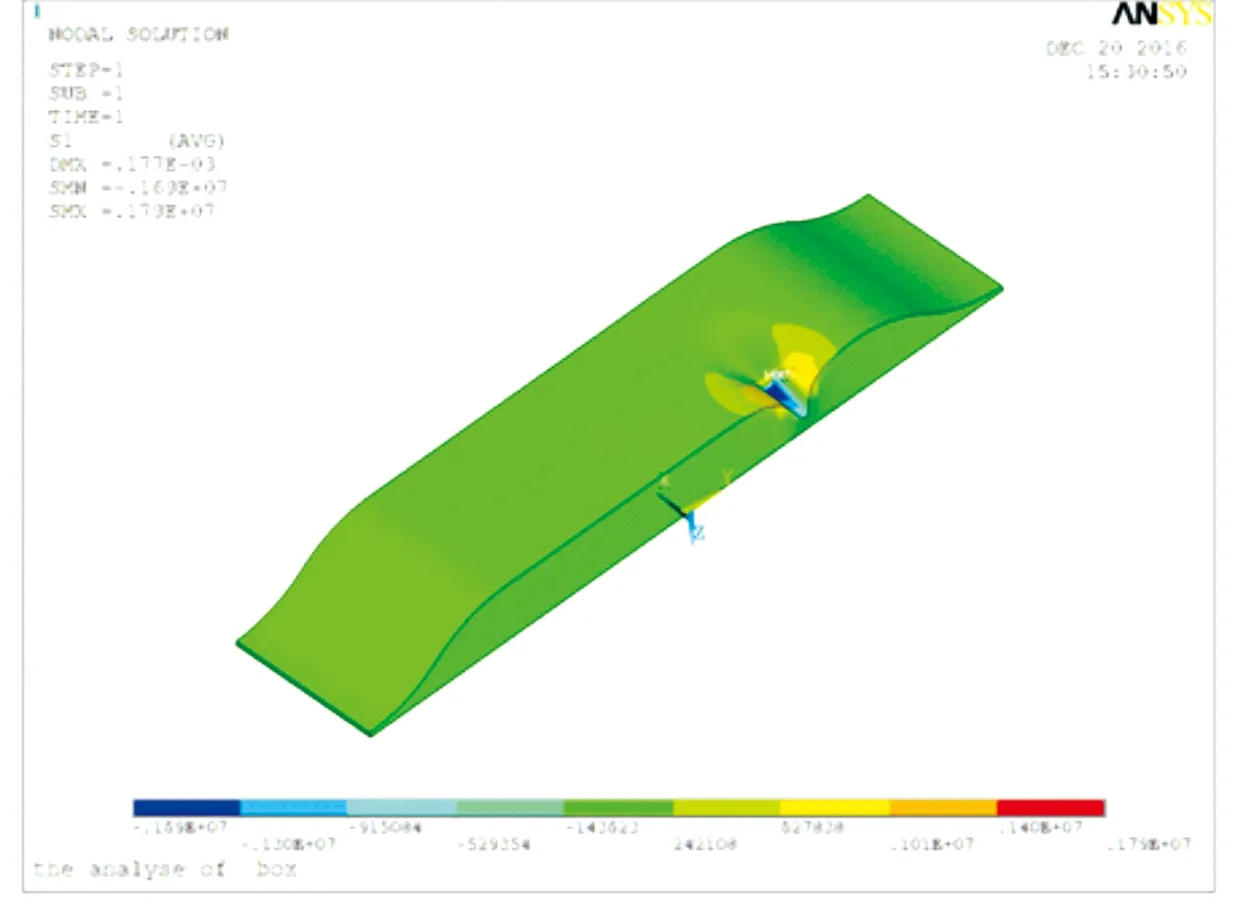
图10 临时支撑处箱梁局部应力主拉应力图

图11 临时支撑处箱梁局部应力主压应力图
由图10、图11可以看出:支撑处箱梁主拉应力1.72 MPa,支撑处箱梁主压应力6.1 MPa,满足规范要求。
4.2 临时支撑处支座垫石局部应力分析
箱梁临时支撑处的最大反力为9 820 kN,支座尺寸为130 cm×130 cm,支座垫石高10 cm。
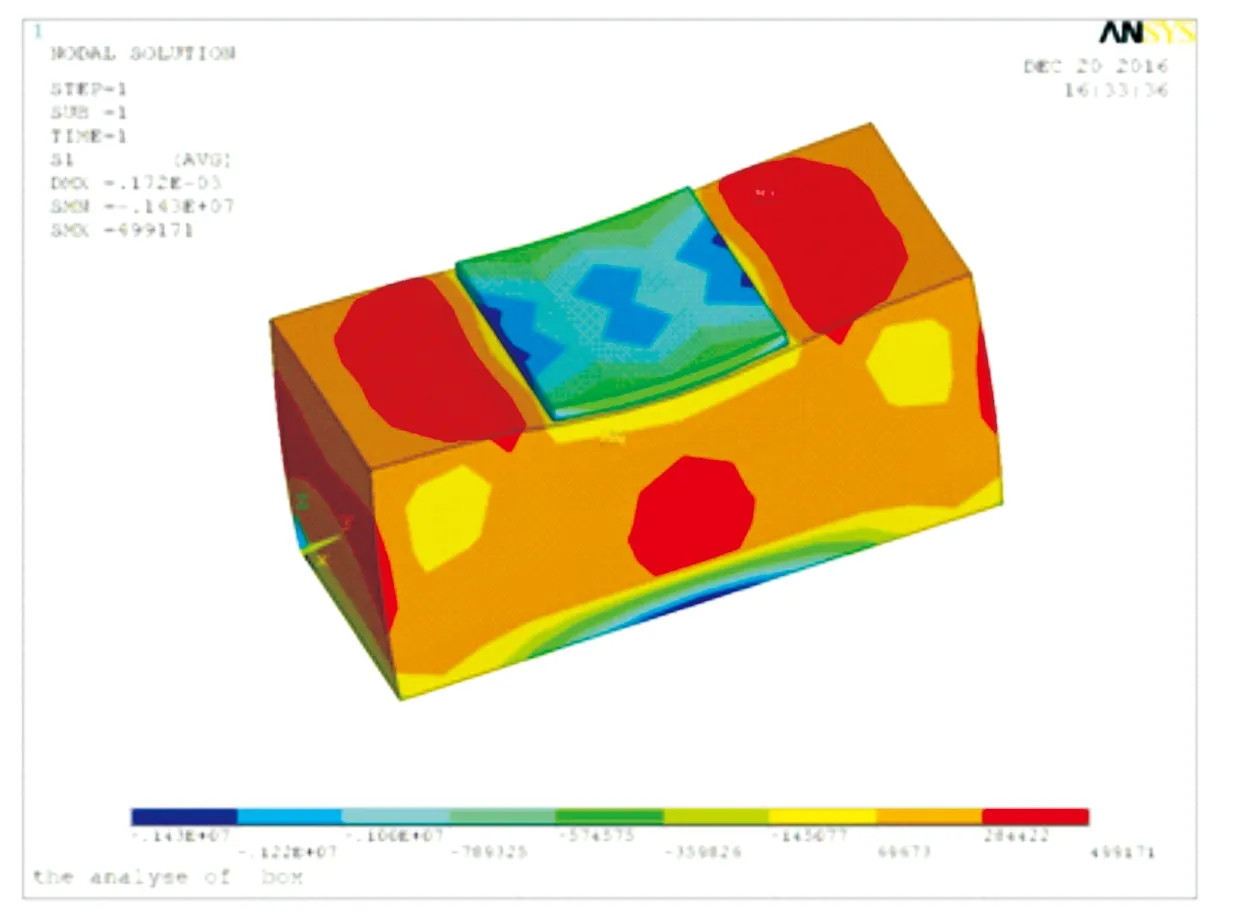
图12 临时支撑处支座垫石局部应力主拉应力图
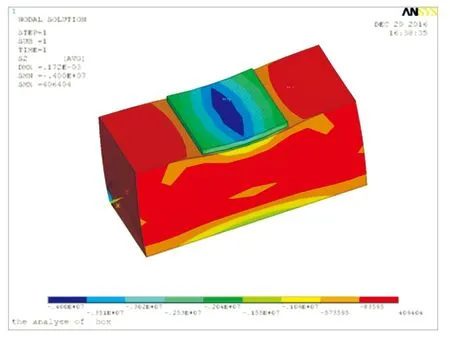
图13 临时支撑处支座垫石局部应力主压应力图
由图12、图13可以看出:支撑处支座垫石主拉应力0.5 MPa,主压应力4.0 MPa,满足规范要求。
5 结论
本文通过对湖滨东路高架桥第一联4 m×35 m连续箱梁顶升改造的施工监控,得出以下结论:
(1) 在箱梁各顶点的反力计算时,应将各顶点位置精确模拟,同时应考虑同一横断面处的千斤顶中出现一个千斤顶不工作的工况分析,才能准确选择千斤顶的型号。
(2) 同一截面处各顶点反力的变化规律并非都一致,H0台千斤顶、H1号墩前排千斤顶、H3号墩后排千斤顶、H4号墩千斤顶的反力由内侧至外侧逐渐增大,其他千斤顶则正好与之相反。
(3) 顶升过程中对箱梁应力增量及各墩台的强迫位移双向监控,应力与位移监控能互相校核,提高监控数据的可靠性,为顶升过程顺利进行提供了保证。
(4) 将箱梁的混凝土抗拉强度设计值作为顶升过程中应力增量的极限值,避免对原箱梁的预应力钢束模拟及箱梁的收缩徐变的计算,计算更简单有效。
(5) 通过对顶升步骤进一步细化,将施工最大顶升步距100 mm拆分成若干子步,便于位移及应力监控,同时能将箱梁的应力增量控制在设计范围内。
[1] 卢伟荣,刘世忠,张瑞杰. 连续梁桥更换支座顶升施工控制[J]. 公路,2012(6):80-86.
[2] 陈智强. 厦门仙岳路改造工程既有桥梁顶升技术[J]. 公路,2012(9):79-87.
[3] 冯明扬,刘世忠,林统励,等. 曲线梁桥旋转顶升改造施工控制[J]. 世界桥梁,2016,44(2):87-91.
[4] 夏洪波,刘世忠,刘志翁,等. 单箱五室连续弯箱梁桥旋转的顶升关键技术[J]. 兰州交通大学学报,2012,31(4):36-40.
[5] 潘玉芳,夏红军. 桥梁顶升施工检测与监控技术[J]. 山东交通科技,2015(4):63-69.
[6] 王文志,陈思甜,邓莎莎,等. 三跨连续梁桥内力调整顶升施工仿真分析与控制研究[J]. 重庆建筑,2016,15(7):39-42.
[7] 吴毅彬,陈历耿,朱绍锋. 云南安宁白塔桥整体同步降落施工工艺[J]. 公路,2011(2):65-68.
[8] 杜方. 连续梁桥顶升技术的若干问题分析[D].西安:西安工业大学,2015.
Key technology for porous continuous box girder jacking up in Xianyue Road construction of Xiamen
LIU Zhi-weng
(GuangdongDaxiongEconomicandTechnicalConsultingCo.,Ltd.,Guangzhou510075,China)
In construction of expressway project of Xianyue Road in Xiamen, in order to avoid the negative social impact of the demolition of the old bridge, make full use of the original bridge structure, on the part of the bridge girder lifting transformation, which has advantages of short construction period and good economic benefits. The first joint of the viaduct is 4×35m prestressed concrete continuous box girder, the total weight of its upper part is more than 8,000 tons, the maximum height is up to 3.6 m, which is difficult for construction and monitoring, and detailed analysis for the key technology is needed in order to ensure the smooth progress of the project.
jacking-up construction; curved box girder; reaction force; forced displacement; local stress
2016-11-11
刘志翁(1979—),男,广东兴宁人,硕士,工程师。
1674-7046(2017)02-0040-08
10.14140/j.cnki.hncjxb.2017.02.008
U445.6
A

