善用“问题”教学 提高教学效率

陈进军

（广东省高州市泗水中学 广东 高州 525200）

【摘要】 在数学教学中，从导入新课到新概念的形成与确立，新知识的巩固与应用，学生思维方法的训练与提高，以及实际应用能力和创新能力的增强，无不从“问题”开始。因此，课堂教学活动实质上就是依据教材内容和学生实际，师生不断发现问题、研究问题、解决问题的活动。课堂教学中的“问题”一方面是依据教材，另一方面也是源于学生，但绝大部分问题需要教师的再加工进行“问题”的设计。那么如何把握课堂教学中“问题”的设计呢？现在从本人的教学实践中谈几点见解。

【关键词】 “问题”教学 教学效率

【中图分类号】 G633.6 【文献标识码】 A 【文章编号】 1992-7711（2017）04-165-01

一、“問题”设计的趣味性

学生是课堂的主体，兴趣是最好的“老师”。充分调动、激励学生学习的求职欲望和积极性是每个教育工作者不断位置奋斗的宗旨。显然“问题”的设计当然也离不开这个宗旨，联系实际，贴近生活就能让“问题”走近学生，使学生对“问题”产生极大的兴趣，这就为研究问题、解决问题提供了基础、动力和保证。

例如讲三角形稳定性时，教师提问“为什么射击瞄准时，用手托住枪杆（此时枪杆、手臂与胸构成三角形）能保持稳定，而能伸缩的铁门要做成平行四边形？”

又如，为了使学生掌握“数轴”的概念，教学中我设计了一个“怎样报告一条东西向的铁路上出现险情的地点”的学习问题，建立“如何确定直线上一点的位置”的教学模型。学生依据生活经验，通过讨论，结合画图，便自然地抽象出“数轴”的概念，理解“方向、原点、单位长度是数轴的三要素，缺一不可。”

二、问题设计的导向性

强化双基，夯实基础是教学工作的基本原则。“问题”取源于双基，通过解决问题又强化了双基，“问题”围绕重点，通过解决问题又突出了重点。让学生在不断的提出问题、解决问题的过程中夯实双基。

例如，在讲三角形中位线性质时，将课本习题做如下改编：“要测量池塘的宽度，身边仅有测量工具皮尺，用皮尺不能量出池塘的宽度，怎样结合本节课所学知识，测出池塘的宽度？”

这样的“问题”设计，既突出了三角形中位线的性质，强化了基础，也突出了这节课的重点。

三、“问题”设计的针对性

“问题”设计的针对性不仅表现在对课堂提问的设计，而且也产生于学生学习中存在的问题，即针对问题有明确意向地进行“问题”设计。

例如，为了强化学生完整思维的习惯，在讲授垂径定理时，选择如下两个题目让学生讨论：

问题1在半径为10cm的⊙O中，弦AB∥CD，AB=12cm，CD=16cm，则AB与CD之间的距离为 。

问题2在半径为10cm的⊙O中，弦AB=12cm，CD=16cm，点M、N分别为AB、CD的中点，则M、N的长的取值范围为 。

对问题1学生的反应是，对图形摆放位置考虑不全；对问题2学生的反应是，不会界定（去找出MN的最大值与最小值）。

实践证明，这样的设计针对性强，学生感触深，收效好。

若x1、x2是关于x的方程的两根，则①x1+x2=

②x1x2= ，③X2/X1+X1/X2= ，④（x1-2）（x2-2）= .

问题2已知方程的两根之差的绝对值为3，则m= 。

问题3m为何值时，方程x2-（m-3）x-m=0的两根都是正数。

问题4已知x1、x2是关于x的方程x2+m2x+n=0的两根，y1、y2是关于y的方程y2+5my+y=0的两根，且x1-y2=2，x2-y2=2，求m、n的值。

问题5设P为三角形ABC的外接圆O的AB上任意一点，AP交BC于D，求证：PB、PC是方程x2-PAx+PA·PD=0的两根

四、“问题”设计的启发性

富有启发性的教学，能够吸引学生的注意力，引起学生的联想，激发学生自己发现问题、思考问题，起到举一反三、触类旁通的作用。所以教学中的问题涉及要注意一问促思，以问促问，促进学生不断地再思考再问。

如教例题“已知：⊙O1和⊙O2外切于点C，BA是⊙O1和⊙O2的共切线，B、A为切点，求证：CB⊥AC”时，我设计了一系列问题。

问题1若把题设条件改为：两圆外离，连结O1O2，分别交⊙O1⊙O于点C、D，其余条件不变，则AC⊥BD是否成立？

问题2若把题设条件改为：两圆相交，连结O1O2，分别交⊙O1⊙O于点C、D，其余条件不变，则AC⊥BD是否成立？

问题3在上述两种情况下，若将O1O2向两端延长，分别交两圆于M、N，则AM垂直BN吗？

问题4解决这类问题的规律是什么？

这样的设计问题可以不断激发学生去思考，有助于强化学生的类比、联想等数学思维。

五、“问题”设计的创新性

思维是从问题开始的，有问题才有思考，有思考才有进行创造性的学习的可能，所以问题是创造的基础。然而，发现为、提出问题是有效开发创新学习潜能的开端，创新学习也由此开始。因此，教师要根据实际情况，通过“问题”设计将科学发现过程简捷地重演于课堂，让学生积极主动地参与学习，给予他们充分的时间和空间，进行探索、猜想、发现。

例如，在弦切角及性质的教学中，我设计了与弦切角及弦切角定理相关的一系列问题，启发、引导学生层层深入发现概念和定理。

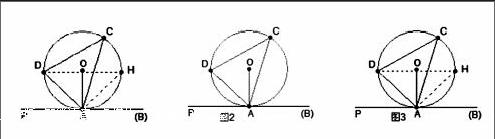
问题1延长⊙O的内接四边形ABCD的BA边至点P，则∠PAD等于哪个角（∠PAD=∠BCD）？想一想如何证明？

问题2如果O的内接四边形ABCD的BA边渐渐往DA方向平移，使直线PA与⊙O相切（点A与点B重合），则∠PAD等于哪个角（让学生分组讨论，并交流结论）想一想如何证明？

问题3依照作平行线的方法，对于问题2有没有其他的新证法？让学生讨论后，启发学生通过点D来作直线MN又如何呢？作DH∥PA，交⊙O于H，连结AH，则∠PAD=∠ACD吗？

问题4象∠PAD这样的角，叫什么角？在解决上述问题的过程中，你发现了什么规律？请你用文字概况出来。（弦切角定理：顶点在圆上，一边和圆相交，另一边和圆相切的角叫弦切角。弦切角定理：弦切角等于它所夹弧对的圆周角）

优化“问题”的设计师课堂教学中必须重视的研究课题，它的效应不单单表现为课堂教学效益的提高，更为重要的是对学生在学习中如何发现问题、提出问题、研究问题、解决问题起着潜移默化的影响，在此良性循环的过程中，学生的思维方法、思维能力、创新意识、创新精神可以不断得到锤炼与增强，这样才能使学生从“学会”逐步走向“会学”。