沿板平面材料梯度变化的二维梯度薄板挠度分析

许杨健，庞宇飞，刘 硕

沿板平面材料梯度变化的二维梯度薄板挠度分析

许杨健1，庞宇飞1，刘 硕2

(1.河北工程大学 土木工程学院，河北 邯郸 056038；2.哈尔滨工业大学 航天学院， 黑龙江 哈尔滨 150001)

采用有限单元法，分析了由Ti-6Al-4V、Al 1100和ZrO2组成的二维功能梯度材料（2D-FGM）薄板的小挠度问题，计算了在不同温度环境下，四边简支受均布荷载的2D-FGM薄板挠度值和四边固支受均布荷载的2D-FGM薄板挠度值，并对本方法进行了正确性检验，给出了2D-FGM薄板挠度分布图。进一步讨论了温度和孔隙率对2D-FGM薄板挠度的影响。结果表明，温度和孔隙率对受载2D-FGM薄板挠度变形影响较为明显，在环境温度不变的情况下，四边固支和四边简支的2D-FGM薄板挠度都随孔隙率的增大而逐渐变大，在孔隙率不变情况下，四边固支和四边简支的2D-FGM薄板挠度都随环境温度的不断升高而逐渐变大。

功能梯度材料薄板；挠度；温度；孔隙率；有限元法

FGM是材料科学领域发展起来的一种新一代非均匀复合材料，它是各国在航空航天高技术领域里的竞争产物。薄板构件在机械、土建、造船、航空等工程领域中应用都很广泛，因此，研究薄板结构性能对各个工程领域都很重要，目前，研究学者们就薄板结构性能做出了大量的研究[1-5]，并获得了丰富的研究成果。Ping Tan等[6]分析了在弹性约束边界下的变刚度复合环形薄板的自由和强迫振动。董文堂[7]导出了四边固支边界条件下的矩形薄板纳维叶解法。Rui Li等[8]得出了基于多点支撑下的矩形薄板自由振动新的解析解。Shilang Xu等[9]对由不同的胶凝材料组成的织物增强混凝土（TRC）薄板进行了耐高温性能试验研究。许杨健等[10]采用层合板有限元法对FGM薄板的瞬态热弹性弯曲问题进行了分析研究。Amin Joodaky[11]对不同边界条件下FGM薄斜板的挠度和应力进行了分析。孙建等[12]计算出了构造挠度函数的系数。目前，大多数研究只在材料属性沿板厚度方向变化上，而沿着板平面材料梯度变化的研究相对很少，曹志远等[13-14]得到了沿板平面材料特性梯度变化的功能梯度板件力学量三维分布状态。本文基于经典薄板理论，利用有限元方法结合Matlab编程求解出2D-FGM薄板受均布荷载下的挠度值，并分别讨论了四边固支和四边简支两种边界条件下，温度和孔隙率对受均布荷载2D-FGM薄板挠度值的影响。可供新型材料挠度变形要求苛刻的航空航天、精密仪器制造等领域作参考，为FGM的设计和应用提供了理论计算依据。

1 模型建立

如图1所示，建立由金属相Ti-6Al-4V、Al 1100和陶瓷相ZrO2组成的2D-FGM矩形薄板模型，考虑材料组分物性值随温度变化，假设材料属性沿x、y轴方向变化，沿薄板厚度无变化。

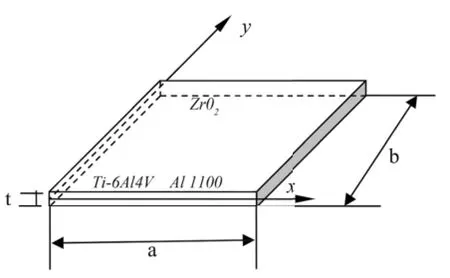
图1 2D-FGM 薄板模型Fig.1 Model of 2D-FGM thin plate

2 FGM薄板弯曲变形有限元方程

为了研究薄板的弯曲变形，则采用经典薄板理论，构造矩形薄板单元。矩形薄板单元共有四个节点，每个节点有3个基本未知数：挠度w，法线绕x轴的转动θx和绕y轴的转动θy。

根据微小位移的假定，位移可表示为：

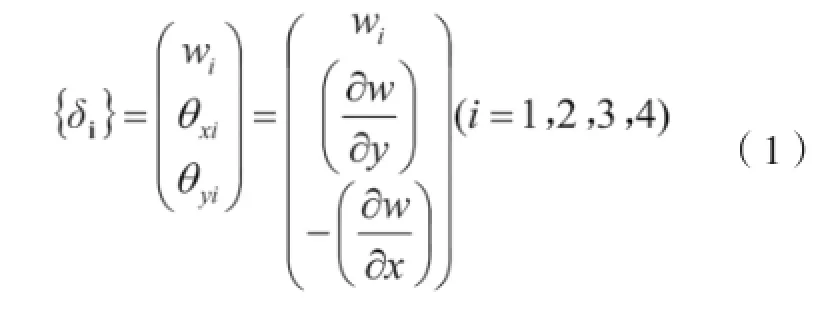
单元节点位移向量为：

取位移函数为：

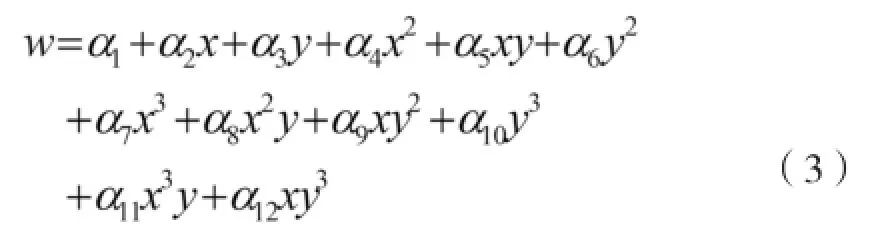
由位移w在薄板单元各个节点处的取值，可以确定w中的12个参量，

式中｛N｝为形函数。

根据虚功原理得：：

式中：｛δ*｝代表虚位移，表示FGM的广义弹性矩阵。而由于｛δ*｝e具有任意性，故得：

式中：［K］ε表示功能梯度材料薄板的单元刚度矩阵。

3 数值算例与分析

3.1 FGM薄板物性值

根据FGM材料研究现状，本文FGM薄板采用由金属相Ti-6Al-4V、Al 1100和陶瓷相ZrO2组成的二维FGM薄板作为研究对象，不考虑组分的影响，考虑物性系数随温度的变化，依据文献[15]，金属Al 1100、Ti-6Al-4V以及陶瓷ZrO2组分材料的变物性物性系数分别如下：

金属Al 1100：

金属Ti-6Al-4V：

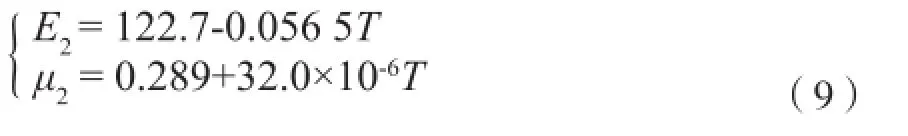
陶瓷ZrO2：

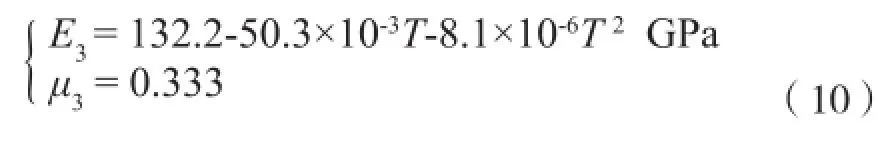
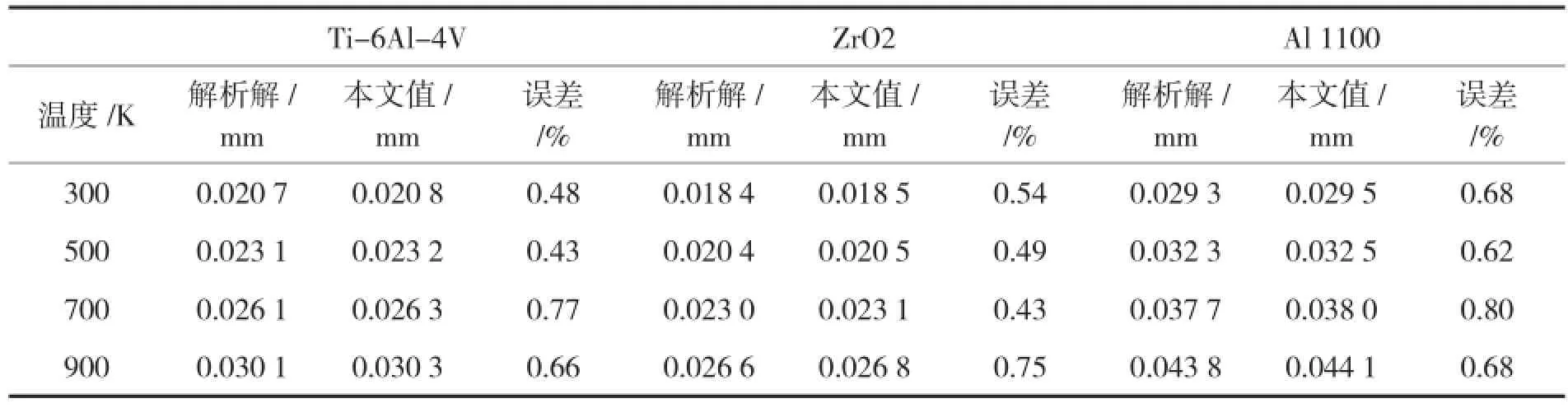
表1 四端固支均质材料薄板受均匀荷载时中心点的挠度Tab.1 Def l ection at center point of clamped supported homogeneous sheet under uniformly distributed loads

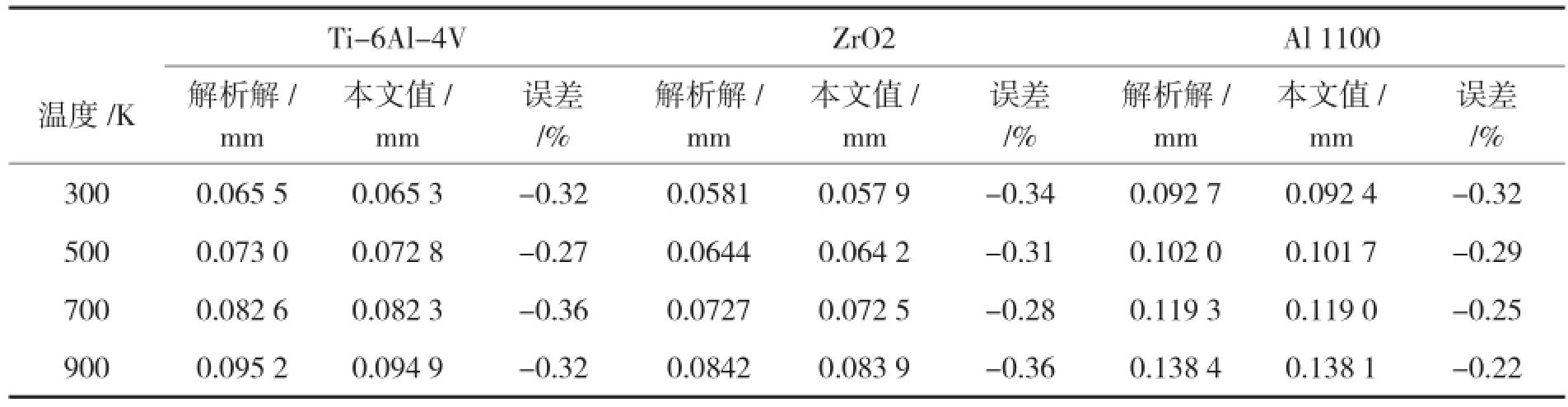
表2 四端简支均质材料薄板受均匀荷载时中心点的挠度Tab.2 Def l ection at center point of simply supported homogeneous sheet under uniformly distributed loads

3.2 正确性检验

为验证本文推导的表达式的正确性，取薄板厚度t为4 mm，a、b都取为100 mm，横向均布荷载取q=0.1 N/mm2，同时将FGM薄板退化为Ti-6Al-4V、Al 1100和ZrO2三种均匀材料薄板，在单元内对材料属性取平均值。将本文有限元计算程序计算的四端固支均质薄板中心挠度与文献[7]的3.7式计算结果对比，四端简支均质薄板的与文献[16]的3.43式计算结果对比。本文方法和文献方法计算薄板中心挠度的结果如表1和表2所示：

通过对比两种方法的计算结果，误差都不超过±0.8%，则本文结果正确。

3.3 温度、孔隙率影响

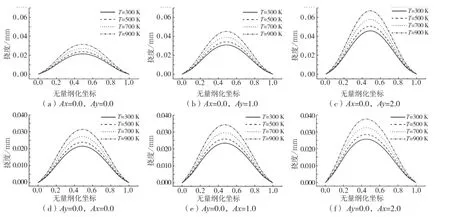
图2 固支2D-FGM薄板的挠度曲线Fig.2 Deflection curve of clamped supported 2D-FGM thin plate

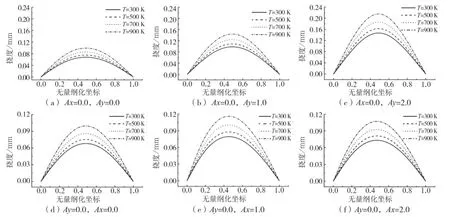
图3 简支2D-FGM薄板的挠度曲线Fig.3 Deflection curve of simply supported 2D-FGM thin plate

图2 和图3表明：不同孔隙率、和不同温度下的四边固支和四边简支2D-FGM薄板的挠度分布图。分析可知：(1)薄板的挠度值从板的边缘到中间逐渐变大，且薄板的最大挠度值靠近板的中心处。(2)在不考虑薄板孔隙率变化的情况下，薄板随环境温度的增加挠度逐渐增大，并且变化率越来越大。如：在图2中Ax=0.0, Ay=1.0时，T=500 K薄板中心点处挠度比T=300 K时增加10.7%，而T=700 K薄板中心点处挠度比T=500 K时增加了14.2%。在图3中Ax=0.0, Ay=1.0时，T=500 K薄板中心点处挠度比T=300 K时增加10.7%，而T=700 K薄板中心点处挠度比T=500 K时增加了14.2%。(3)在不考虑环境温度变化的情况下，薄板挠度随孔隙率的增加不断变大。如：在图2中T=700 K时，Ay=0.0，Ax=1.0薄板中心点挠度比Ay=0.0, Ax=0.0时增加了8.3%。取T=500 K时，Ax=0.0，Ay=1.0薄板中心点挠度比Ax=0.0，Ay=0.0为时增加了43.9 %。在图3中T=300 K时，Ay=0.0，Ax=1.0薄板中心点挠度比Ay=0.0，Ax=0.0时增加了7.4 %，T=900 K时，Ax=0.0, Ay=1.0薄板中心点挠度比Ax=0.0，Ay=0.0时增加了45.0%。

4 结论

1）通过对由Ti-6Al-4V、Al 1100和ZrO2组成的2D-FGM薄板算例的挠度计算，计算结果和文献给出的结果是一致的，说明了本文方法正确可行，给出了不同孔隙率下2D-FGM薄板挠度分布。

2）根据算例计算结果分析可知，无论FGM薄板四端简支还是四端固支，环境温度和孔隙率对受载FGM薄板挠度影响均较为明显，薄板挠度随着环境温度的升高而增大且变化率也在增大，随着孔隙率变大挠度也在逐渐增大。

3）在本文的相同条件下，四边固支薄板比四边简支薄板挠度值小，更适合承受大的荷载。

[1]MIRSALEHI M，AZHARI M，AMOUSHAHI H.Stability of thin FGM microplate subjected to mechanical and thermal loading based on the modified couple stress theory and saline finite strip method[J].Aerospace Science and Technology,2015;47(8)：356-366.

[2]TAN P, NIE GJ.Free and forced vibration of variable stiffness composite annular thin plates with elastically restrained edges[J].Composite Structures,2016;149：398-407.

[3]LIN R, TIAN Y, WANG P C.New analytic free vibration solutions of rectangular thin plates resting on multiple point supports[J]. International Journal of Mechanical Sciences,2016;110：53-61.

[4]IIDA J, HASEBE N.Stress intensity factors of a rhombic hole with symmetric cracks under uniform transverse thin plate bending[J].Engineering Fracture Mechanics,2016,156：16-24.

[5]王春玲,高 典,刘俊卿.横观各向同性弹性半空间地基上四边自由各向异性矩形薄板弯曲解析解[J].力学季刊,2015，36(1)：95-104.

[6]PING TAN, G.J. NIE.Free and forced vibration of variable stiffness composite annular thin plates with elastically restrained edges[J].Composite Structures,2016,149：398-407.

[7]董文堂.固支边矩形薄板的纳维叶解法[J].黄石高等专科学校学报, 1999,1(15)： 1-4.

[8]LI R, TIAN Y, WANG P C.New analytic free vibration solutions of rectangular thin plates resting on multiple point supports[J].International Journal of Mechanical Sciences,2016,110：53-61.

[9]XU S L, SHEN L H, WANG J Y.The high-temperature resistance performance of TRC thin-plates with different cementitious materials： Experimental study[J]. Construction and Building Materials,2016,115：506-519.

[10]许杨健, 赵志岗.梯度功能材料薄板瞬态热弹性弯曲有限元分析[J].工程力学,2001,18(1)：71-81.

[11]JOODAKY A, JOODAKY I, HEDAYATI M.Deflection and stress analysis of thin FGM skew plates on Winkler foundation with various boundary conditions using extended Kantorovich method[J].Composites： Part B,2013;51(3)：191-196.

[12]孙 建,胡 洋.均布和静水压力作用下固支矩形薄板力学特性[J].应用力学学报，2015,32(6)： 908-914.

[13]曹志远,程红梅.沿板平面材料梯度变化功料板件分析[J].力学季刊,2007,28(2)：203-208.

[14]曹志远,程红梅.沿板平面材料组分变异功梯度板件分析[J].同济大学学报,2007,35(11)：1460-1465.

[15]王 飞.变物性二维梯度板热弹性行为[D]. 邯郸：河北工程大学, 2014.

[16]曲庆璋.弹性板理论[M].北京：人民交通出版社出版,1999.

（责任编辑 王利君）

Deflection analysis of two-dimensional graded thin plates varying along plane direction

XU Yangjian1,PANG Yufei1,LIU Shuo2

(1 College of Civil Engineering, Hebei University of Engineering, Hebei Handan, 056038;2 School of Astronautics, Harbin Institute of Technology, Heilongjiang Harbin, 150001 )

The small deflection of the two dimensional functionally graded material (2D-FGM) thin plate (Ti-6Al-4V, Al 1100 and ZrO2) is analyzed by the finite element method(FEM) .The deflection value of 2D-FGM thin plate subjected to uniform distributed load with four edges simply-supported or clampedsupported is calculated under different temperatures. At the same time, the accuracy of this method is examined. The deflection distribution diagrams are obtained. Effects of temperature and porosity on the deflection of 2D-FGM thin plate are discussed. The results show that the influence of temperature and porosity on the load 2D-FGM thin plate is obvious. In the case of constant ambient temperature, the deflection of 2D-FGM thin plate with four edges clamped-supported and four edges simply-supported increases with the increasing of porosity. Under the condition of constant porosity, the deflection of 2D-FGM thin plate with four edges clamped-supported and four edges simply-supported increases with the increasing of temperature.

functionally gradient material thin plate; deflection; temperature; porosity; finite element method

TB333

A

1673-9469（2017）01-0034-04

10.3969/j.issn.1673-9469.2017.01.008

2016-09-08 特约专稿

河北省自然科学基金资助项目 (E2011402033)

许杨健(1956 -)，男，四川富顺人，教授，从事固体力学计算、有限元应用和梯度功能材料方面的研究。