发行者视角下保函支持商业票据定价研究

王 进，何建敏，汤正洪

(东南大学经济管理学院，江苏 南京 211189)



发行者视角下保函支持商业票据定价研究

王 进，何建敏，汤正洪

(东南大学经济管理学院，江苏 南京 211189)

在商业票据职能和资产支持商业票据融资潜在风险基础上，提出保函支持商业票据发行融资方式。考虑保函支持商业票据发行的客观基础和主观动因，通过分析发行过程中各参与者之间利润分配确定发行者收益函数。进一步利用累积前景理论，引入价值函数和决策权重函数构建发行者的效用函数，得出发行者效用最大化的保函支持商业票据最优定价及最优定价约束条件。最后，结合部分参数的现实取值，对定价与所选取的自变量之间的关系进行仿真。结果表明，在既定的参照点和基础收益函数结构下，发行者效用最大化条件下的最优定价与主体风险属性和市场随机干扰无关，发行者表现出风险中性特征；最优定价和最优发行规模在不同凹凸性的支配下，均随着分享系数的增加而单调递增。

发行者视角；保函；商业票据；累积前景理论；定价

1 引言

持票人对商业票据(Commercial Paper，CP)即时或未来现金流有请求权和追索权，且可以贴现和转贴现。这体现了CP作为支付手段和融资工具的两个重要职能[1]，可为资金实力较弱的中小企业延期支付行为和摆脱融资困境提供有力保障。在我国具有短期融资功能的CP又称为“短期融资券”，但规模很小[2]，融资功能未得到充分发挥。而利用CP进行融资在国外较为普遍，且随着资产证券化技术的不断成熟，资产支持商业票据(Asset Backed Commercial Paper，ABCP)于20世纪80年代逐步兴起。借助资产证券化思想，金融机构或企业把能够产生稳定现金流的资产(如资产支持证券、应收款项、抵押贷款等基础资产)出售给受托机构，受托机构以此为资产池发行商业票据进行融资。

基础资产的加入在提升ABCP融资潜力的同时又带来了新的风险因素，如：信用支持由单一或少数机构提供[3]，导致基础资产信用风险的分散不足；基础资产与票据期限易出现错配[4]，面临展期风险[5]等。保函又称保证书，是指合规金融机构或个人应申请人请求，向第三方开立的一种书面信用担保凭证。保证在申请人未能按双方协议履行责任或义务时，由担保人代其履行一定金额、一定期限范围内的某种支付责任或经济赔偿责任。可见，将能够产生稳定现金流的资产附加保函后作为ABCP基础资产，上述风险因素可得到有效化解。

本文将“保函支持商业票据”界定为：具有融资职能的资产支持商业票据，其产生现金流的基础资产由保函进行信用担保(下文称“保函资产”)。在实践中，被要求在商业合同基础上附加保函的企业多为中小企业，其数量庞大且在地域和行业上比较分散。因此，无论是基础资产，还是保函出具机构和出具时间都更加多元化，有效化解了传统ABCP发行中原始债务人信用风险较大以及基础资产流动性风险抵御能力不足等问题。同时，由于商业信用的广泛运用，大量企业持有延期支付款项及其保付保函，即保函资产。为提高资金利用效率，持有人存在变现需求，这为发行保函支持商业票据提供了客观基础。而在主观方面，新的融资工具的发行需要考虑的核心问题之一在于其定价能否体现参与各方，尤其是发行者的主观利益诉求。

具体来说，对于票据潜在发行者而言，其发行意愿主要取决于成本和收益的权衡。就成本而言包括两个方面：第一，隐性学习成本，包括发行者是否熟悉相关发行流程和技术细节，若不熟悉则需要额外付出成本进行“学习”；第二，显性货币成本，包括发行者在发行过程中向基础资产持有者支付的购买成本，向其他金融服务机构支付的费用等。

在隐性学习成本方面，我国现有票据定价研究多局限于货币市场的利率相关问题讨论[6] [7]，而本文所探讨的保函资产支持商业票据(下文在不引起混淆的情况下简称“票据”)在本质上属于资产证券化范畴，因而发行者需要借鉴资产证券化技术进行定价。因此，票据发行流程上与其它资产的证券化过程并无太大差异，而在技术细节上最大的差异在于定价方面。因为目前无论实务界和理论界对资产证券化的关注重点都在中长期资产上，其定价方法主要以提前偿付模型[8-12]、违约概率模型[13-18]和期权调整利差(Option Adjusted Spread，OAS)模型[19-22]为主。其中提前偿付模型与违约概率模型对历史数据依赖程度较高，而实际中，我国缺乏有关票据发行的历史数据，如提前偿付与违约。因为一般来说短期资产的债务人不会有提前偿还的动机，经济环境和债务人产生较大变化的可能性也不大。而OAS模型需要一个类似资产的收益率作为参考以计算贴现率而现实中，相对于住房抵押贷款等长期资产而言，由于短期融资产品规模较小，发行者在定价时很难找到与其收益相近的参考基准，为此，使用OAS亦具有一定的难度。除此之外，短期资产与中长期资产在现金流、规模、风险以及支付结构等方面均存在着较大的差异。目前，对商业票据定价的研究比较少，利用保函相关资产进行融资的理论研究和实践活动更少，国内仅有少量文献化进行了定价研究，如汤正洪等[23]基于无套利原理和风险减值因子的定价模型研究了附加保函的应付款资产支持证券定价。

而在显性货币成本方面，主要体现发行过程中各参与者的利润分配上。票据的现金流主要来源于原始债务人的本息支付，对于参与者而言，这一大于本金的本息支付成为整个发行过程的利润来源，因而该利润的分配情况决定了各机构的参与热情。同时由于市场上缺乏相关短期证券产品的参照，作为潜在发行者的金融机构在向原始基础资产持有人和相关中介服务机构支付相对固定的成本和费用后，将通过对票据的定价来实现与投资者的剩余利润共享“博弈”，这一博弈特性在以机构投资者为主的票据市场更为显著。同时，由于现金流具有“或有”特性，在这一情境下发行者和投资者需要对潜在收益和损失进行考量，从而表现出“行为人”特征。

票据的短期和或有资产特性以及发行过程定价“博弈”特点，导致现有的主要定价模型，即提前偿付模型、违约概率模型和期权调整利差模型等并不适用本文研究对象。Kahneman和Tversky[24-25]于1979年提出了前景理论，后来对这一理论进行了改进，提出了累积前景理论(Cumulative Prospect Theory，CPT)。近年来，前景理论与累积前景理论被用于资产定价的研究中来，如张永莉等[26]、邹高峰等[27]和郑君君等[28]。本文鉴于现有的资产证券化定价研究在票据定价研究的局限性，创造性地提出利用累积前景理论刻画潜在发行者在票据发行过程中和投资者之间利润分配不确定性的考量。通过引入价值函数和决策权重函数来构建发行者的效用函数，推导出票据的最优定价及最优定价约束条件，并对结论进行仿真分析，得出发行金额和发行价格与分享系数之间的关系，以期为票据的发行者和投资者等提供参考。

2 发行者收益分析

与资产证券化发行流程类似，保函支持商业票据发行者从持有保函资产的机构或个人(简称“持有人”)处购买保函资产，向银行等中介机构支付相关服务费用后，组建特殊目的机构(Special Purpose Vehicle，SPV)，并最终确定发行价格，向投资者销售。因此，票据发行的最优资本结构就是确定总收益在持有人、发行者、银行等服务机构和投资者之间的分割[29]，如图1所示。

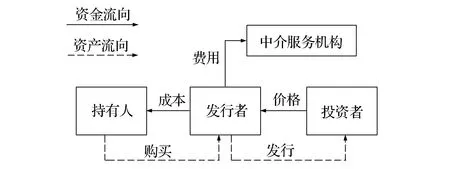
图1 保函支持商业票据收益分配

从发行者视角来看，向持有人支付的收益率主要受原始债务人的保证金比率水平ω和履约率η影响，可设为a=F(ω,η)=R-η(d-fω)，其中R为非违约基础资产的平均收益率，d>0和f>0为待估参数。根据上式可知，a与平均保证金比率成正比，ω越大意味着分配给持有人的收益越低；而η与a成反比，暗示了违约率越高，分配给持有人的收益越低，实际定价中，ω和η可以根据原始债务人的经验数据得到。因此，a就表示了在不考虑供求关系的情况下，扣除持有人收益后的剩余。另外，发行者向银行等中介服务机构的支付比率为常数值c，由行业管理确定。

在向持有人和相关中介机构支付必要成本和费用后，假设剩余收益率r的函数形式为r=a-bq，a>b>0。其中q为发行规模，a定义为非违约保函资产总收益率扣除支付给持有人购买资产成本后的剩余。b为衰减系数，表示受供求关系的影响，随着保函支持商业票据发行金额的增加，发行者从持有人购买保函资产的价格递增，因而收益率递减。b暗示了受供求关系的影响，发行者从持有人购买保函资产的价格是递增的。由于特定的金融工具交易市场，b应是一个较稳定的值。因此，票据发行过程中发行者的收益取决于：发行金额、发行者与投资者之间对收益r=R-η(d-fω)-bq分割比率，为方便下文分析，将该分割比率定义为π。

3 基于累积前景理论的发行者效用

因保函支持商业票据为短期融资，本文假设发行者拟采用折价方式发行三个月期的票据，投资者于票据到期日获得票面金额，且发行间隔与基础资产存续期相同，则发行者的收益函数如式(1)所示。

x=π(qr+θ)-cq

(1)

其中，x为发行者净收益；q为任意一次发行的票据的票面总金额；c为发行单位金额票据时，发行者向银行等中介服务机构支付的费用率；r与前文含义相同，为支付持有人的收益后，由发行者和投资者分享的剩余收益率，表示为q的函数，技术上满足r′(q)<0；π为发行者对剩余收益(qr)的分享系数，满足π∈[0,1]。θ为收益的市场随机扰动项，与正态分布相比，韦伯分布能够更好的刻画市场波动的真实情况[30][31][32]，故假设θ服从韦伯分布，其概率密度与分布函数分别如式(2)和式(3)所示。

(2)

(3)

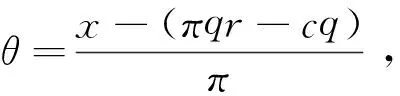
x～f(x)=

(4)

(5)

式(4)和式(5)表明x也服从韦伯分布，且E(x)=πqr-cq。假设参照点k=0，根据CPT，发行者的价值函数和权重函数分别为：

(6)

(7)

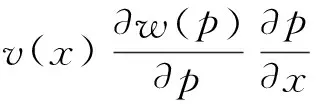
(8)

由于p=1-F(x)|x≥0，则结合式(7)可知：

(9)

得出：

(10)

(11)

首先考虑x≥0时的发行者效用。将(6)和(10)式代入(8)式右端的第一部分，则为：

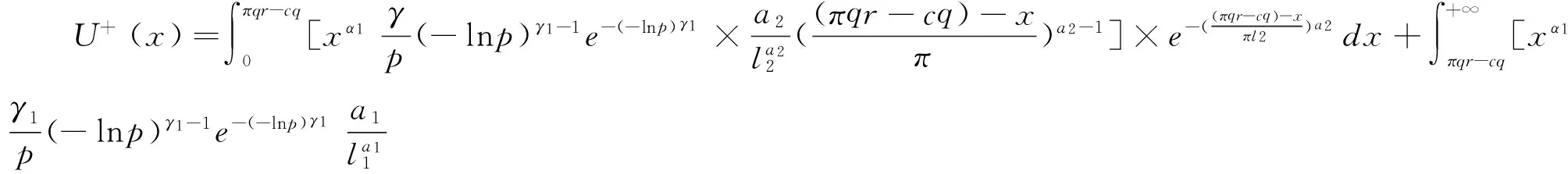
(12)

采用换元法，令y=x-πqr+cq，则式(12)变换为：

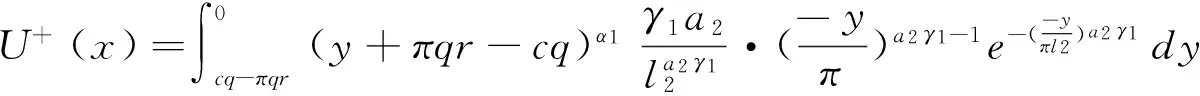
(13)

根据积分的定义，可求得到当x≥0时，发行者的效用为：

(14)

其中Γ(·)为伽玛函数，γ(·,·)为不完全伽玛函数，分别为：

(15)

同理，将(6)和(11)式代入(8)式右端的第二部分，得到x<0时的发行者效用为：

(16)

将(14)和(16)式代入(8)式，得到发行者的总效用函数为：

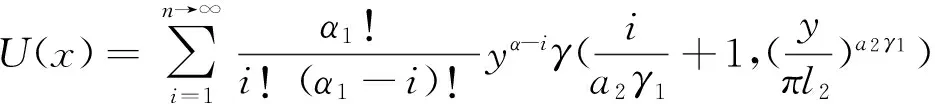
(17)

至此，基于保函支持商业票据发行过程的收益分配和CPT，经推导得到发行者的总效用函数，为下文最优定价的确立做准备。

4 最优定价与约束条件

4.1 理论最优定价

由前文分析知，(17)式为发行保函支持商业票据时CPT下发行者的总效用函数。显然，基于发行者视角的票据最优定价应满足发行者效用最大化条件。而式(17)中，变量个数较多，因而选择合理的可以作为求解效用最大化的自变量尤为重要。如前文所述，从票据发行过程中收益分配结构看，发行者净收益函数(1)由参数ω、η、c、π、r、q决定。其中ω和η可以根据原始债务人的经验数据得到；c为行业约定费用率；分享系数π由发行者和投资者竞争决定，不能完全由发行者决定；净收益率r是q的单调递减函数，反映了发行者与基础资产持有人之间的客观供求关系，其函数的具体形式应为外生的。因而，票据发行过程中，发行者能够有效控制的变量仅为q。假设发行者可以自由选择不同的发行金额，即q∈[0,+∞)，且为连续的，则在q的定义域内发行者效用最大化条件可以表示为式(18)。

UMAX(x)=

(18)

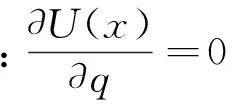
(19)

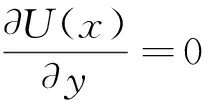
同时，U(x)对q的二阶条件为：

(20)

根据一阶条件得：

(21)

x*=E[π(q*r+θ)-cq*]=(aπ-c)q*-bπ(q*)2

(22)

从票据发行的收益分配结构看，发行价格等于投资者购买价格，故可以通过发行面值扣除投资者净收益的方式求得。根据(21)和(22)式，在发行者效用最大条件下，票据发行中分享给投资者的期望净收益为：

(23)

设单位票据的面值为V，采用贴现发行(投资者以低于V的价格购买证券，并于证券到期日获得V)，因而单位票据发行份数为q*V-1。则基于发行者视角的票据最优定价为：

(24)

上式中，由于参数a、b、c和V均为外生，因此，最优价格P*仅由分享系数π决定。虽然本文根据累积前景效用理论推导了基于发行者视角的票据最优定价模型，但是最优定价模型中没有发行者风险态度、损失厌恶系数、权重函数参数以及市场干扰分布参数。这意味着发行者风险态度、市场干扰等因素对最优定价没有影响，采用何种效用函数均应得到相同的定价结论。其主要原因可以解释为发行者效用最大化的位置取决于基础收益函数x=π(qr+θ)-cq，而非累积效用理论中的主体属性参数。

4.2 机会成本约束下的最优定价

根据前文推导的发行者最优定价模型可知，对于任意一个分享系数π，都存在唯一一个的最优价格P*。从经济意义上分析，发行者进行保函支持商业票据发行的基本条件应为rs≥0，rs为票据发行收益率。然而，鉴于理性人的逐利性特征，发行者在票据的发行周期内将面临若干机会成本。本文界定发行者的机会成本为筹集与任意一次发行金额相同资金的筹资成本rj，因此，发行者发行票据的动机必须满足条件rs≥rj，即发行保函支持商业票据的收益率不小于发行者的筹资成本。由于最优发行价格等于单位保函资产购买成本Cb、发行者净收益x*q*-1V与中介服务机构费用cV之和，即Cb+x*q*-1V+cV=P*，则票据的发行收益率rs等于发行者净收益除以购买单位票据的成本。

(25)

将(22)、(23)和(24)式带入(25)式得

(26)

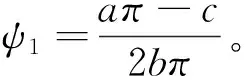
aπ2+(arj-c-2rj-2crj)π+crj=0

(27)

根据二次线性方程的求根公式，若(arj-c-2rj-2crj)2-4acrj≥0，式(27)存在两个实数根。根据现实中三个月期的筹资成本rj、a和c的经验值可知，4acrj非常小，式(必有两个实数根为：

(28)

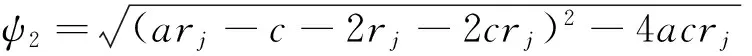
因此，不等式rs≥rj可表示为：

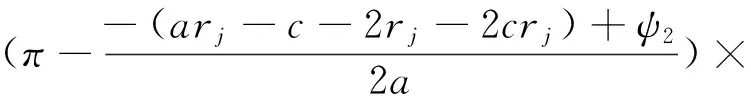
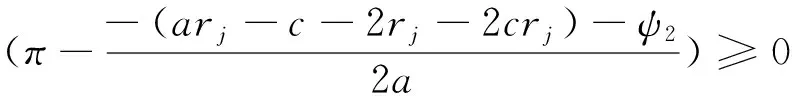
(29)

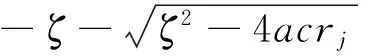
(30)

5 基于小贷公司保函资产历史数据的仿真案例

为了检验基于发行者视角的保函支持商业票据定价结果是否合理，并揭示分享系数与发行金额之间的动态关系，本文首先根据定价模型和约束条件计算出在特定参数条件下的最优定价区间，同时根据江苏省小额贷款公司应付款保函业务的实际数据对相关参数进行经验估计，最后对最优价格、最优发行金额与分享系数之间的关系进行仿真和分析。根据《江苏省小额贷款公司 应付款保函业务管理暂行办法》规定，应付款保函由小贷公司开户企业或个人申请签发，到期后小贷公司负责承兑并向原始债务人提示付款。因而，该保函同时具有基础资产和担保凭证的特性。在保函到期前，保函持有人可以向小贷公司进行贴现，小贷公司之间也可进行转贴现。因而，大量持有应付款保函的小贷公司有出售该资产给发行者进行融资的需求。

由前文分析知，发行者能够控制的变量为分享系数π，而π又由a、c、rj决定，其中a=F(ω,η)=R-η(d-fω)。因此在进行仿真前需要根据各外生变量确定π的取值范围。图2是在保证金比率水平ω以及履约率η不变的情况下，根据a=F(ω,η)=R-η(d-fω)，对剩余收益率a与平均保证金比率和债务履约率的乘数d，f进行数值仿真得到。可以看出，a与d，f形成一张平面，a的取值随d的增大而单调递减；a的取值随f的增大而单调递增。根据式a=F(ω,η)=R-η(d-fω)可知，a与平均保证金比率成正比，平均保证金比率越大意味着分配给小贷公司的收益越低；而原始债务人的履约率与a成反比，违约率越高分配给小贷公司的收益越高，这暗示了在基于小贷公司应付款保函的票据发行过程中，真实出售原则对发行者的风险补偿随着原始债务人违约率的增加而增加。以来源于“江苏省人民政府金融工作办公室”的江苏省小贷公司保函业务历史数据为例，单位金额保函资产的总收益一般为11%，原始债务人申请保函业务的保证金比率约ω为20%，履约率η为98.5%，则可估计出a=0.09，b=1×10-10。

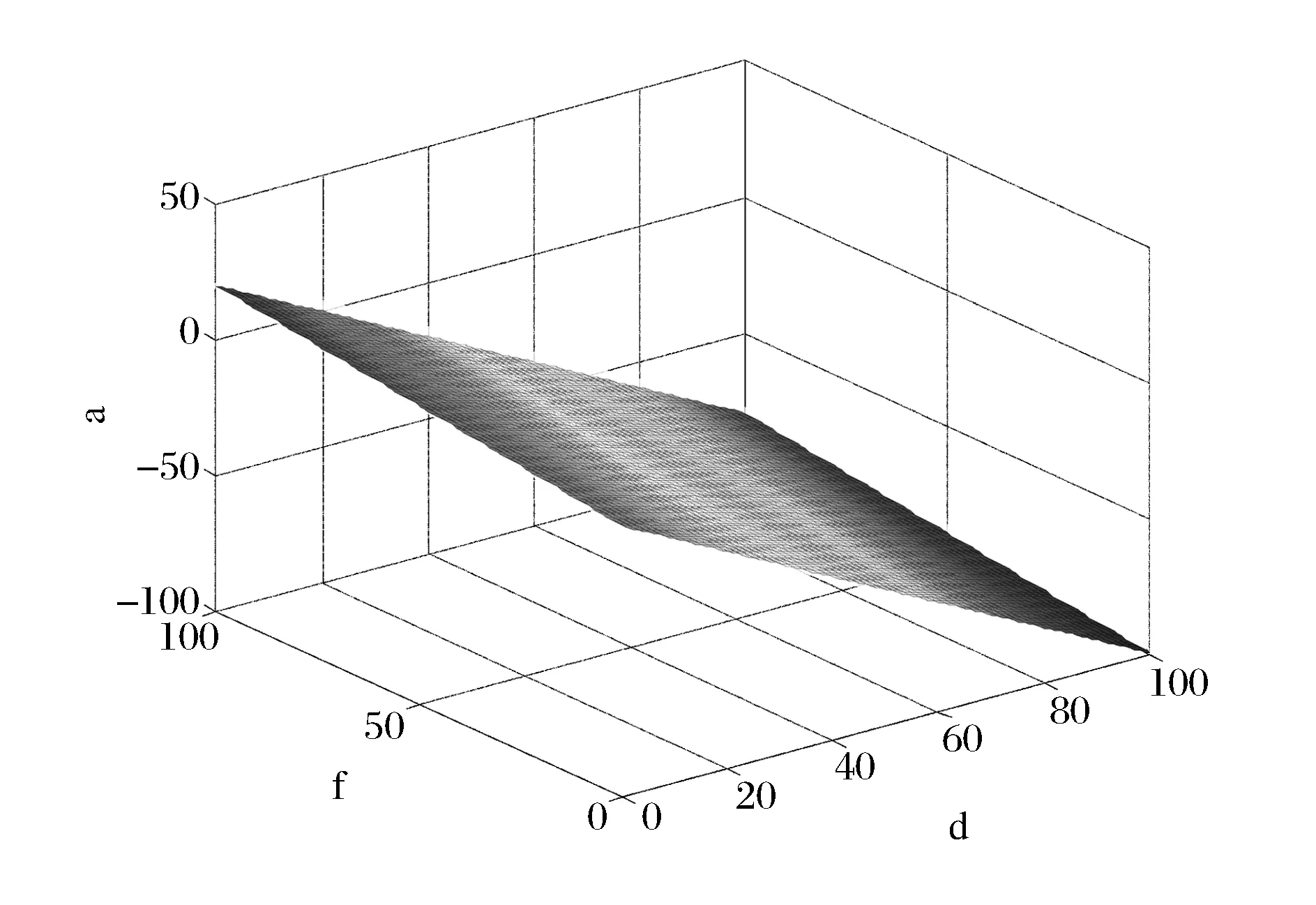
图2 d，f和a的仿真图像

同时，根据三个月期短期资产证券化实际数据，中介服务费收入为0.6%至2%之间，本文假设为c=0.015；根据2015年1月至4月的三个月期银行间平均同业拆借利率，假设发行者维持经营的三个月最低报酬率rj=0.0125；若保函资产证券的面值V为50万元，根据(30)式可求出分享系数π>0.3181。将此区间带入(24)式可求出保函支持证券最优发行价格为P*>4.77×105。直观上看，该最优价格是可接受的，说明本文基于发行者视角的票据定价模型在实际中是可行的。由于在票据最优定价模型中，发行者仅能影响分享系数π，因此，在约束条件0.3181<π<1条件下，本文将分析分享系数π与发行金额q*、发行价格P*的仿真关系，分别如图3和图4所示。

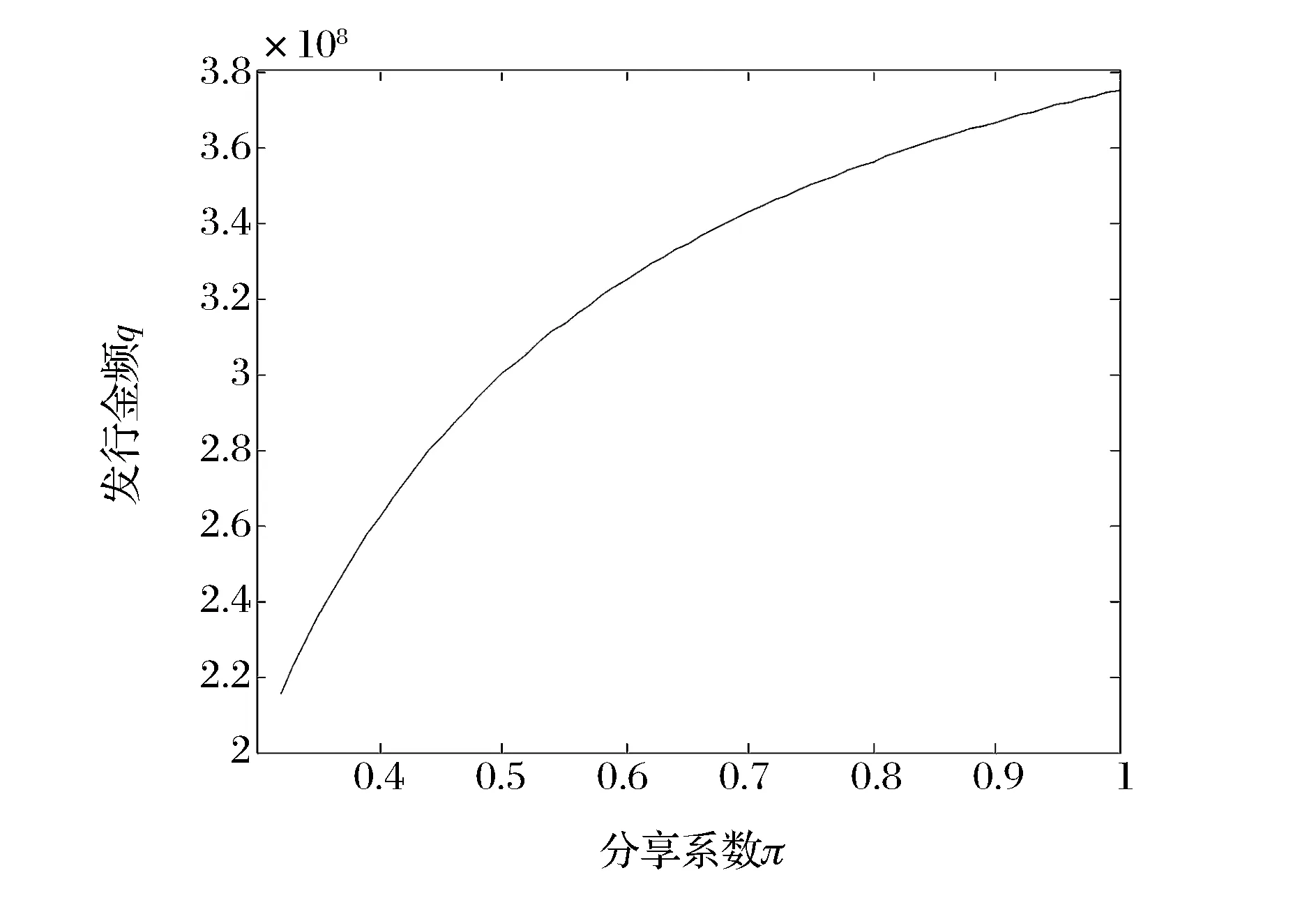
图3 分享系数π与发行金额q*的关系

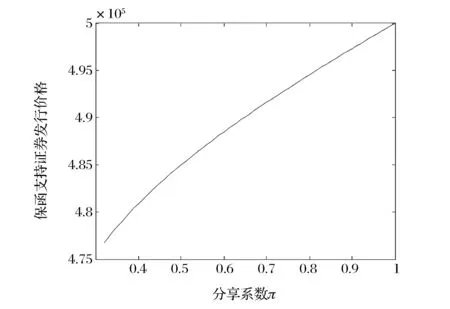
图4 分享系数π和发行价格P*的关系

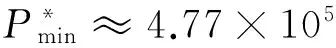
6 结语

根据保函支持商业票据期限、发行方式、现金流特征以及在各主体之间的收益分配关系，本文基于发行者视角构造了基本收益模型，在累积前景效用理论框架下推导了基于发行者视角的保函支持商业票据最优定价模型和约束条件，并得到以下结论。

(1)发行者风险属性、权重函数以及市场干扰分布参数不影响最优定价模型结果。根据累积前景效用理论可知，发行者的效用由价值函数和权重函数决定。然而，本文得出的最优定价模型中没有发行者风险属性、权重函数以及市场干扰分布参数，仅与发行者的净收益模型相关。这意味着采用累积前景效用理论推导的最优定价模型与采用期望效用理论推导的结果是一致的。罗彪等[33]在研究企业委托代理中的最优契约报酬分配时也得到了相似的结论。

(2)最优定价的仿真结果在可接受的范围之内。根据市场上存在的短期融资利率和江苏省小贷公司应付款保函业务数据，估计发行者基本收益模型参数，以三个月期保函资产为例进行仿真分析。在满足约束条件基础上计算的最优发行定价在(4.77×105,5×105]的范围内，因此保函支持商业票据的发行价格是可接受的，是本文模型有效性的有力佐证。

(3)发行金额、最优价格均与分享系数正相关。通过仿真分析可知，在约束条件范围内，最优发行金额q、最优价格P*均随分享系数π的增大单调递增，当分享系数π=0.3181时，取得最小值；当π=1时，取得最大值。虽然仿真关系表明分享系数越大对发行者越有利，但是本文的最优定价仅仅是基于发行者视角的，最优价格的实现还需要考虑投资者的决策行为。这暗示了保函支持商业票据市场的供求关系和双方的议价能力将确定最优价格，并落于(4.77×105,5×105]之内。

[1] 刘春志. 商业票据业务发展[J]. 中南财经政法大学学报, 2003，(6):38-43.

[2] 沈红波, 廖冠民. 信用评级机构可以提供增量信息吗——基于短期融资券的实证检验[J]. 财贸经济, 2014，(8):62-70.

[3] 刘传哲, 史国庆. 资产支持商业票据:中小企业融资新渠道[J]. 证券市场导报, 2006,(7):69-73.

[4] 陈颖, 王胜邦, 张守川. 次贷危机对新资本协议实施的影响[J]. 国际金融研究, 2008,(10):51-60.

[5] 邢天才, 袁野. 次贷危机时期的资产支持商业票据市场——基于GMM方法对美国ABCP市场的检验[J]. 宏观经济研究, 2012,(7):72-79.

[6] 潘永明, 李雪, 张婷婷. 基于信用增级视角的中小企业集合票据定价研究[J]. 金融经济学研究, 2013,(4):26-35.

[7] 李合怡, 贝政新. 银行间市场中期票据信用利差的影响因素研究[J]. 审计与经济研究, 2014,(4):107-112.

[8]ChristopoulosAD,JarrowRA,YildirimY.Commercialmortgage-backedsecurities(CMBS)andmarketefficiencywithrespecttocostlyinformation[J].RealEstateEconomics, 2008, 36(3): 441-498.

[9]ZhouTi.Indifferencevaluationofmortgage-backedsecuritiesinthepresenceofprepaymentrisk[J].MathematicalFinance, 2010, 20(3): 479-507.

[10] 魏成龙, 王述评. 个人住房抵押贷款提前偿付率实证研究—基于建元2005资产证券化产品资产池的模型[J]. 经济管理, 2011,(4): 160-164.

[11] 孔凝, 吴文锋. 中国个人住房抵押贷款支持证券提前偿付率实证研究 [J]. 上海金融,2013,(12): 132-135.

[12] 范为, 俞乔, 刘江波. 基于Monte-Carlo模拟的CMOs多因素定价模型研究[J]. 管理评论, 2014, 26(5):12-22.

[13] 周颖, 李璞. 应收账款证券化融资选择问题研究[J]. 中央财经大学学报,2007,(2): 91-96.

[14]KauJB,KeenanDC,YildirimY.Estimatingdefaultprobabilitiesimplicitincommercialmortgagebackedsecurities(CMBS)[J].TheJournalofRealEstateFinanceandEconomics, 2009, 39(2): 107-117.

[15]PinheiroFAP,SavoiaJRF.Securitizationofreceivables-ananalysisoftheinherentrisks[J].BrazilianReviewofFinance, 2009, 7(3): 305-326.

[16] 叶文忠, 杨招军,郑毅. 抵押贷款证券的效用无差别定价[J].中国管理科学, 2010, 18(4): 21-27.

[17]ChangWE.Acaseofelusivecross-bordertransaction:Securitizationofinternationalairlinesfutureflowreceivables[J].KoreaUniversityLawReview, 2011, 10(12): 97-115.

[18]FabozziFJ,VinkD.Lookingbeyondcreditratings:FactorsinvestorsconsiderinpricingEuropeanasset-backedsecurities[J].EuropeanFinancialManagement, 2012, 18(4): 515-542.

[19]EricssonJ,RenaultO.Liquidityandcreditrisk[J].TheJournalofFinance, 2006, 61(5): 2219-2250.

[20]PanJun,SingletonKJ.DefaultandrecoveryimplicitinthetermstructureofsovereignCDSspreads[J].TheJournalofFinance, 2008, 63(5): 2345-2384.

[21]LiuZhangyong,FanGangzhi,LimKG.Extremeeventsandthecopulapricingofcommercialmortgage-backedsecurities[J].TheJournalofRealEstateFinanceandEconomics, 2009, 38(3): 327-349.

[22] 陈蓉, 郭晓武. 期权调整利差(OAS)及其应用研究[J].统计研究, 2005,(8)： 44-47.

[23] 汤正洪, 何建敏, 韩扬.附加保函的应付款资产支持证券定价研究——一个基于无套利原理和风险减值因子的定价模型[J].北京航空航天大学学报(社会科学版), 2014, 27(4):82-87.

[24]KahnemanD,TverskyA.Prospecttheory:Ananalysisofdecisionunderrisk[J].Econometrical,1979,47:263-291.

[25]TverskyA,KahnemanD.Advancesinprospecttheory:CumulativerepresentationofUncertainty[J].JournalofRiskanduncertainty, 1992, 5(4): 297-323.

[26] 张永莉, 邹勇.基于前景理论的行为资本资产定价模型的构建[J].统计研究, 2013(12): 39-41.

[27] 邹高峰, 张维, 张海峰, 等. 中国市场条件下的前景理论资本资产定价模型[J].系统工程学报, 2013, 28(3): 355-361.

[28] 郑君君, 韩笑, 邹祖绪. 引入前景理论的股权拍卖异质投标者竞价策略演化均衡研究[J]. 管理工程学报, 2015, 29(4): 109-116.

[29] 张勇, 杨招军, 罗鹏飞. 信贷资产证券化模式选择与产品设计[J]. 中国管理科学, 2016, 24(12): 1-9.

[30]DaviesGB,SatchellSE.Continuouscumulativeprospecttheoryandindividualassetallocation[R].WorkingPaper,UniversityofCambridge, 2004.

[31]LaherrereJ,SornetteD.Stretchedexponentialdistributionsinnatureandeconomy:“Fattails”withcharacteristicscales[J].TheEuropeanPhysicalJournalB-CondensedMatterandComplexSystems, 1998, 2(4): 525-539.

[32]SornetteD,SimonettiP,AndersenJV.φq-fieldtheoryforportfoliooptimization:“Fattails”andnonlinearcorrelations[J].PhysicsReports, 2000, 335(2): 19-92.

[33] 罗彪, 王成园. 基于累积前景理论的报酬契约模型设计与分析[J]. 中国管理科学, 2013, 21(5): 121-128.

StudyontheGuaranteeofAssetSecuritizationPricingfromthePerspectiveofBondIssuers

WANGJin，HEJian-min，TANGZheng-hong

(SchoolofEconomicsandManagement,SoutheastUniversity,Nanjing211189,China)

To alleviate funding pressure of enterprises, especially middle and small-sized ones, and to assure application of deferred payments in business activities, the concept of guarantee backed commercial paper was proposed based on the functions of commercial paper and potential funding risks of asset backed commercial paper. The pricing of the proposed paper, whose underlying assets are backed by guarantee, was also studied. The key point of financing tool issuance is that whether the pricing of it could reflect interests of issuers and investors at the same time after paying cost to other stakeholders. And for a new tool, the interest of issuers must be the first consideration. Like asset backed commercial paper, guarantee backed commercial paper is also a generalized kind of asset securitization. However, the traditional pricing methods of asset securitization, which focus on the medium and long term asset, do not apply to guarantee backed commercial paper. Therefore, the concept of utility maximization was applied in the present paper to obtain reasonable price and its constraint conditions. The potential issuer exhibits more behavioral rather than rational traits given the bargaining power of institutional investors, which are more common in commercial paper markets, and the consideration of risk and payoff affected by contingency. Thus, the cumulative prospect theory was used to capture different risk attitudes when individual facing gains or losses, and utility function of the issuer was presented via value and weight functions. Results have shown that mathematical model of pricing is just relevant to net profit and does not take risk attribute, weight function and parameter of market turbulence into account. Thus, the issuer it risk neutral in this circumstance. Furthermore, a case study was conducted by substitute parameters in pricing model and its constraint conditions with data gathered from relevant guarantee business of micro-credit companies in Jiangsu province. Simulation between total profit, issuance scale, price and concerned variables are performed with given reference point and profit function. Results have shown that this pricing method could help issuers to determine a reasonable range of pricing, and that the final price of the guarantee backed commercial paper is depend on supply-demand relationship and bargaining power of both sides in the market.

the perspective of the issuer；guarantee；asset securitization；cumulative prospect theory；pricing

1003-207(2017)03-0001-09

10.16381/j.cnki.issn1003-207x.2017.03.001

2016-02-14；

2016-07-15

国家自然科学基金资助项目(71671037，71371051，71201023)；教育部人文社会科学研究规划基金项目(16YJA630026)；江苏省社会科学基金青年项目(15GLC003)

何建敏(1956-)，男(汉族)，江苏无锡人，东南大学经济管理学院，博士生导师，教授，研究方向：金融风险管理,E-mail：hejianmin@seu.edu.cn.

F830.91

A