偏心梁和非偏心梁建模方法合理性分析
王健明,卢慧敏,戴睿,张少雄
(1.上海船舶研究设计院,上海 201203;2.中国船级社 江苏分社,南京 210000;3.武汉理工大学 交通学院,武汉 430063)
偏心梁和非偏心梁建模方法合理性分析
王健明1,卢慧敏1,戴睿2,张少雄3
(1.上海船舶研究设计院,上海 201203;2.中国船级社 江苏分社,南京 210000;3.武汉理工大学 交通学院,武汉 430063)
为了验证《结构共同规范》、《双壳油船规范》规定的非偏心梁和CSR散货船规范规定的偏心梁属性定义的合理性,采用一加筋板模型,利用MSC.Patran/Nastran对比在复杂弯曲状态下板梁组合模型有限元收敛解与同量级全板元位移及应力结果,发现偏心梁模型结果与全板元相对误差能够满足工程需求,非偏心梁不能满足工程需求。对比一条散货船和一条双壳油船发现,偏心梁与非偏心梁应力差距最大可达100.70 MPa,与普通钢的屈服极限235比值为42.85%。偏心梁模型计算结果更加符合实际,验证了CSR-H摒弃非偏心梁的合理性。
CSR;偏心梁;非偏心梁;复杂弯曲
CSR(common structural rules)《散货船共同规范》和CSR《双壳油船共同规范》是2本独立的规范,对其中不协调部分进行协调是必然趋势。2009年,GBS在IMO的大力推动下,于MSC 87次会议确定了GBS符合性验证导则,确定了对IACS《共同结构规范》进行GBS符合性验证。在IACS理事会C60会议上,对协调后的《共同结构规范》(CSR-H)的性质和涵盖范围进行了明确。首先,CSR-H是协调一致、合二为一的一本规范;第二,HPT工作组协调后的规范内容必须符合GBS的要求,列入项目目标范围。这样,CSR-H的重要性上升到了新的高度,未来CSR-H规范一方面应该是完成协调要求的规范,同时也是满足GBS要求的规范[1]。
为了适应GBS的要求,CSR-H更讲究规范背后的技术论证,相关的技术背景文件和资料必须要满足IMO GBS审核的要求[1]。2012年7月,IACS向工业界发布了CSR-H(EXTERNAL RELEASE 1 JUL 2012)。CSR和CSR-H对于有限元直接计算(direct strength analysis,DSA)中,梁单元建模方法存在差异。在有限元结构设计分析中,对梁的受力形式以及在空间放置方式等的理解直接影响整个分析计算结果[2]。
CSR《散货船规范》规定梁截面属性采用偏心梁,以板中面处的节点M作为主节点,梁的形心处节点S作为从节点,认为主从节点间用刚臂连接。梁的抗弯惯性矩按梁的形心轴计算[3]。然而,CSR《双壳油船规范》规定,梁截面形式采用非偏心梁,把节点取在板的中面处,梁的形心取在板的中面上。梁的抗弯惯性矩考虑梁本身截面和带板(两边均为纵骨间距的一半)来计算[4]。具体截面形式见图1和图2。
2012年7月发布的CSR-H协调《共同结构规范》摈弃了CSR《双壳油船共同规范》规定的非偏心梁截面属性,取的是偏心梁截面属性[5]。为对比分析这两种截面形式的可靠性,采用一加筋板将偏心梁和非偏心梁收敛解与全板元结果进行对比,并以两种截面属性,分别计算一条散货船和一条油船,得出主要纵向构件应力差值,以验证CSR-H梁单元属性的合理性。
1 板架分析论证
1.1 计算对象
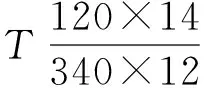
计算坐标系以船底板左端面中点为原点,x轴向前为正方向,y轴向左舷为正方向,z轴向上为正方向,见图3。
1.2 技术路线
建立上述加筋板模型,采用以下2种边界条件和载荷进行计算分析。
1)模型1。边界条件为四周刚性固定,底板承受均布水压力4 MPa;采用以下分级网格模型,800 mm×800 mm、400 mm×400 mm、200 mm×200 mm、100 mm×100 mm、50 mm×50 mm、25 mm×25 mm和12.5 mm×12.5 mm进行计算。
取A点(1 200,0,0)和B点(1 200,800,0)的位移、XComponent和von Mises值与板厚量级模型(12.5 mm×12.5 mm)进行比较,分析得到收敛解的网格大小[6]。
2)模型2。边界条件为自由支持,前后两端承受拉力,并承受面内均布水压力,以模型1得到的有限元收敛解的网格大小(经验算为50 mm×50 mm的网格)为基准建立全板元、偏心梁和非偏心梁3种模型,分析比较哪种梁截面和全板元最贴合。
1.3 收敛性证明
从表1可知:偏心梁模型的位移和von Mises值在网格大小为50 mm×50 mm时已经收敛,相对板厚量级网格误差最大为0.3%,故可以认为50 mm×50 mm网格计算结果为板梁组合模型的收敛解。而非偏心梁在模型1的边界条件和载荷作用下,中面应力恒为0,这与实际情况相悖。
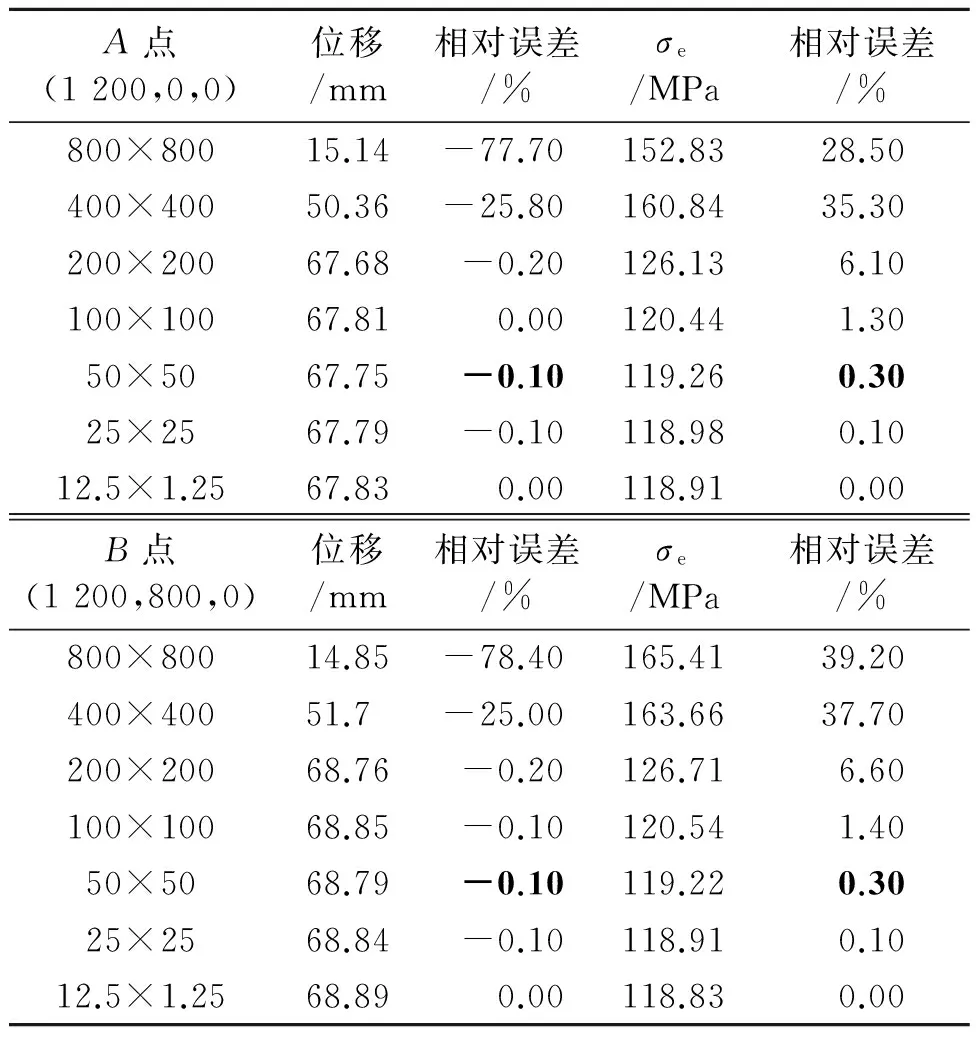
表1 随着网格逐级细化,A、B点位移和von Mises值 及板厚量级网格的误差
以下分析可采用50 mm×50 mm全板元应力结果作为基准,对比偏心梁和非偏心梁2种计算模型的应力和应变值,判断出哪种梁截面形式更加准确。
1.4 复杂弯曲时,偏心梁和非偏心梁位移及应力结果与全板元的对比
利用偏心梁和非偏心梁分别建立加筋板的计算模型,模型均以50 mm为基准建立网格,边长比尽量接近1∶1。将纵骨用板单元模拟,仍然以50 mm为基准划分网格,建立全板元模型。采用如下边界条件和载荷进行:四周自由支持,左右两侧节点承受150 kN的水平拉力,方向相反;底板承受均布水压力0.2 MPa。
四周边界约束z向位移,对称轴ab约束y位移和绕x、z轴向转角,对称轴cd约束x位移和绕y、z轴向转角。
由于梁改板及节点力分配不协调的问题,为了保持板梁组合模型与全板元载荷的一致性,纵骨与底板交点不加节点力,在两侧节点施加水平拉力是为了模拟实际底板是复杂弯曲状态。
1.5 应力对比单元
取图4和图5所示单元为位移和应力对比位置,其中Stiff-for、Stiff-mid和Stiff-end 3个单元形心为船底板纵骨中和轴位置。
1.6 全板元结果
表2、表3为全板元对比单元的位移及应力值,图6、图7为应力云图。
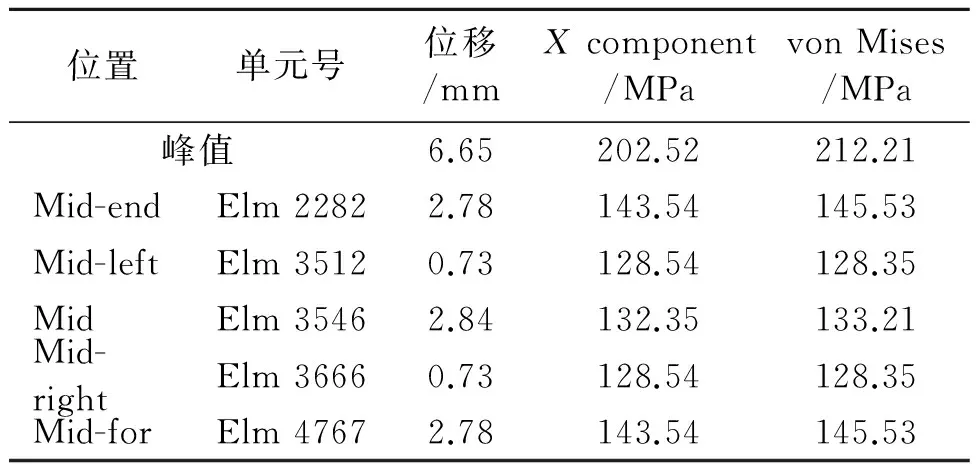
表2 外底板对应单元的位移、X Component和 von Mises值(全板元模型)

表3 纵骨对应单元的X Component值(全板元模型)
1.7 对比分析
偏心梁和非偏心梁与全板元相对误差见表4和表5。
1)从图4选定的底板的5个单元对比可知,偏心梁模型板单元形心处位移相对全板元最大误差为-6.84%,非偏心梁最大是240.77%;Xcomponent相对全板元误差最大为-0.54%,非偏心梁最大是-9.03%;von Mises相对全板元误差最大为-0.55%,非偏心梁最大是-9.84%。

表4 偏心梁和非偏心梁单元形心处位移、X component和von Mises与全板元相对误差
2)底板对比可知,偏心梁模型板单元形心位移峰值相对全板元最大误差为-0.60%,非偏心梁最大是15.19%;Xcomponent峰值相对全板元误差最大为0.00%,非偏心梁最大是0.02%;von Mises峰值相对全板元误差最大为3.72%,非偏心梁最大是21.25%。

表5 偏心梁和非偏心梁梁单元轴心处X component 与全板元相对误差
3)从图5选定的3个单元对比梁单元轴向应力Xcomponent可知,偏心梁模型梁单元轴心处相对板单元对应位置的误差最大为-5.96%,非偏心梁最大为28.15%。
2 实船舱段对比分析
分别采用某型散货船和油船进行实船验证,计算思路见图8。
主要纵向构件应力差值云图如图9和图10。
由图9和图10可知,CSR规定的偏心梁和非偏心梁截面属性对于计算结果影响较大,其中散货船最大差值为37.5 MPa,油船最大差值为100.7 MPa,与普通钢屈服极限比值为42.85%。
3 结论
1)非偏心梁模型对于承受面内压力和轴向拉伸的复杂弯曲下,加筋板的位移及应力结果相对同量级全板元误差超过工程允许范围。
2)偏心梁模型板单元应力及梁单元轴心处应力与全板元模型应力基本吻合,能够满足工程计算的要求。
3)验证了CSR-H摒弃非偏心梁,采用偏心梁截面属性的合理性。
[1] XU Hua. Invisible opportunity of CSR-H[J]. China ship survey,2011(2):33-34.
[2] 孙秀峰,谷良贤,姜晋庆.MSC.NASTRAN中偏心梁的有限元建模问题[J].弹箭及制导学报,2005,25(1):249-250.
[3] IACS.Common structural rules for bulk carrier[S].2012.
[4] IACS.Common structural rules for double hull oil tank[S].2012.
[5] IACS.Common structural rules for bulk carriers and oil tankers[S],1 JUL 2015.
[6] 杨刚.一种MSC.NASTRAN中偏心梁有限元计算结果修正方法[J],科学技术与工程,2011,11(33),83-86.
[7] 张少雄,陈南华,张伟.8 000 t级江海直达驳船的全船结构强度直接计算[J].船海工程,2005(5):39-41.
[8] 杨永谦.有限元法及其在结构分析中的应用[M].大连:大连海运出版社,1992.
Modeling Method Rationality Analysis of Eccentric Beam and In-Plane beam
WANG Jian-ming1, LU Hui-min1, Dai Rui2, ZHANG Shao-xiong3
(1.Shanghai Merchant Ship Design and Research Institute, Shanghai 201203, China;2.Jiangsu Branch of China Classification Society, Nanjing 210000, China;3.School of Transportation, Wuhan University of Technology, Wuhan 430063, China)
In order to validate the rationality of the in-plane beam in common structural rules (CSR) for double hull oil tankers and the eccentric beam in CSR for bulk carriers, a stiffened plate model was established in MSC Patran/Nastran. In the complex bending state, the convergence of displacement and stress in beam-plates combination model and the data in full plate element with the same mesh size was contrasted. It was found that the differences between the eccentric beam model and the full plate element are small, which can meet the engineering requirements, while the in-plane beam model can't meet the engineering requirements. Through a comparative analysis of a bulk carrier and a double hull tanker, the largest gap of the in-plane beam and full plate model can reach 100.70 MPa. So the eccentric beam modeling method is more reasonable.
CSR; eccentric beam; in-plane beam; complex bending
10.3963/j.issn.1671-7953.2017.02.010
2016-08-25
王健明(1989—),男,硕士,助理工程师
U661.43
A
1671-7953(2017)02-0044-05
修回日期:2016-09-20
研究方向:船舶结构设计

