几何参数对加肋凹型锥环柱极限承载能力影响
毛开仁,吴梵,张二
(海军工程大学 舰船工程系,武汉 430033)
几何参数对加肋凹型锥环柱极限承载能力影响
毛开仁,吴梵,张二
(海军工程大学 舰船工程系,武汉 430033)
利用ANSYS有限元软件分析大尺寸加肋凹型锥环柱在静水压力作用下的破坏机理,采用单一变量法,分析几何参数对加肋凹型锥环柱结合壳的极限承载能力和破坏模式的影响。减小半锥角、适当增加环壳厚度及环壳两端肋骨尺寸有利于提高环壳的稳定性和结构整体的极限承载能力,提高环壳肋骨腹板尺寸,能更有效提高整体结构的极限承载能力;增加肋骨的水平方向尺寸能更好地提高环壳的稳定性。
加肋凹型锥环柱结合壳;大尺度;极限承载能力;破坏模式
加肋锥环柱作为一种新型潜艇耐压连接结构,相关的研究已经论证了其优越的力学性能。结构上,凹形结合壳较凸形结合壳有着更不利的受力特性。因此研究人员对于凹形结合壳的研究更为关心。文献[1]运用分区样条等参元法分析了结构参数对凹形结合壳的应力和稳定性的影响,发现0°~30°内半锥角越大,嵌入环壳段的优势越明显,增大环壳与柱壳半径比可降低环壳段中部的纵向弯曲应力,并提出了环壳中部增加一档肋骨的建议。文献[2]对凹形加肋锥环柱的环壳加强方式进行了讨论,对环壳中部增加肋骨与环壳适当加厚2种方式,以“应力放大系数”作为衡量加强效率的指标,并进行了模型试验研究,表明环壳适当加厚是较为优越的加强方式。文献[1]的分析方法仅适用于弹性阶段应力和稳定性分析,文献[3-4]指出模型试验中应变片无法区分弹性与塑性应变,无法准确、全面地了解评价壳体状态,进而提出加肋轴对称壳体结构的非线性应力分析方法,并通过试验的验证。文献[5]提出基于缩减弹性模量的理念,建立加肋轴对称组合壳塑性极限载荷计算的有限元方法,并通过算例进行了验证。由于试验条件限制,上述凹结合壳都是基于小尺寸模型研究,大比例甚至实尺寸的研究较少。由于大模型的结构材料及结构尺寸对实际的研究结果会产生部分影响,因此本文以大尺寸的加肋凹形锥环柱为研究对象,采用ANSYS有限元软件对其破坏过程进行仿真分析,研究几何参数变化对其极限承载能力及破坏模型的影响规律,为加强或结构优化提供参考。
1 计算模型
圆柱壳半径R1=4 000 mm,半锥角a=20°,柱壳、环壳和锥壳板厚度为40、63和45 mm,结合壳长L=7 430 mm,肋骨腹板尺寸bh=28 330 mm2,翼板尺寸为tf=35 135 mm2;锥壳端边界为l4=300 mm,锥壳段肋骨间距l3=600 mm;环壳段肋骨间距l2=680 mm,柱壳端边界l0=350 mm,柱壳段肋骨间距l1=700 mm,材料弹性模量E=210 MPa,泊松比为μ=0.3,屈服极限σs=785 MPa。结构示意于图1。
壳体与肋骨均采用ANSYS中的shell181单元。边界条件为锥壳边界固支,柱壳边界仅放松轴向(轴向移动)。壳板单元划分为100 mm,肋骨单元划分:周向为100 mm,径向为70 mm。图2所示为有限元模型示意图。
不考虑初始几何缺陷并假设材料为理想弹塑性(即采用双线性等向强化本构关系),采用Van Mises屈服准则,破坏条件即为局部Van Mises应力达到屈服,破坏时的载荷为极限承载能力。
求解方法采用非线性有限元中的弧长法进行加载分析,弧长法是增量非线性有限元分析中沿平衡路径迭代位移增量的大小(即弧长)和方向确定载荷增量的自动加载方案,通过追踪整个加载过程中实际的载荷、位移关系,获得结构破坏前后的全部信息。考虑大变形的情况下,总载荷设为15 MPa,子步数为20,最大弧长半径乘子比例为2,最小弧长半径乘子比例为0.000 1。
2 破坏机理分析
图3为模型最大位移点的载荷-位移曲线图。
由图3可见,在第8个载荷步时(第8个数据点),结构达到了最大承载,极限承载能力即为9.375 MPa。
由于模型达到极限承载点时结构还未失效或破坏,还有较高的承载能力,无法判断其破坏模式。利用弧长法平衡路径迭代追踪至下降阶段较小的载荷值时,观察对应的变形云图可判断结构的破坏模式。图4为载荷步60时模型的位移云图。
由图4可见,模型在环壳处出现周向失稳形态,环壳以及环壳靠近锥壳的一档肋骨(3号肋骨)呈现明显的8个波的周向失稳形态,而环壳靠近柱壳的一档肋骨(4号肋骨)未出现明显的周向失稳。从应力水平分析,由于3号肋骨的半径大于4号肋骨,因而3号承受的环向应力大于4号肋骨。仔细观察可以看出,3号肋骨的端部位移要大于根部的位移,环壳靠近3号肋骨部分位移大于环壳中部,因而可以判断为环壳3号肋骨失稳,引起环壳壳板发生失稳。
3 结构参数分析
采用单一变量法研究不同结构参数如半锥角、环壳厚度、环壳肋骨间距、环壳肋骨尺寸等对极限承载能力和破坏模式影响。
锥柱结构的半锥角一般处于10°~30°之间,因而本文研究的半锥角从10°~30°之间,每隔2°取一值进行计算。计算结果见表1。
由表1可见,半锥角增大,模型极限承载能力逐渐下降,半锥角在10°~16°模型破坏模式为锥壳屈服,半锥角在18°~30°破坏模式为环壳周向8个波失稳。环壳失稳破坏模式下,极限承载能力下降速度随半锥角的增加较锥壳屈服破坏模式更快,说明环壳对半锥角变化更敏感。
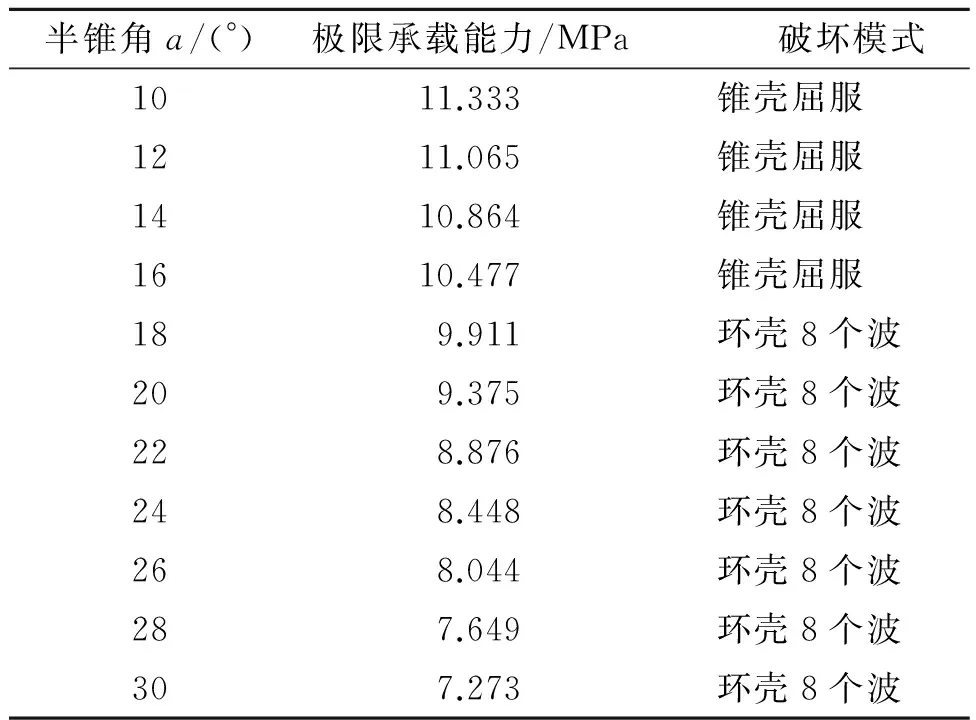
表1 不同半锥角下的极限承载力及破坏模式
由于凹形结合壳存在壳板纵向应力合成的附加径向力与静水压相叠加,造成结合部位环向应力较大,即使凹结合壳间嵌入环壳,其环向应力依然较高,因此环壳需要加厚。环壳加厚多少合适,这是设计人员所关心的。针对具体的结构,需要进行相关的计算。算例中按照相关应力要求将锥壳、环壳、柱壳厚度分别设计为45、63、40 mm,环壳与柱壳的厚度比已超过1.5,但从仿真结果分析,环壳处出现周向失稳破坏,说明该处的稳定性问题较为突出。现将环壳的厚度做如下调整,以分析环壳厚度对结构的极限承载力与破坏模式的影响。计算结果如表2。

表2 不同环壳厚度下的极限承载力与破坏模式
从表2可以看出,环壳厚度在49~67 mm范围内,模型的极限承载能力随壳板的厚度增加呈现上升的变化,此段范围内模型的破坏模式为环壳周向失稳。当环壳厚度超过67 mm时,模型模式由环壳失稳转变为锥壳屈服,同时,环壳厚度继续增加,对整体极限承载能力影响很小。
从环壳厚度变化幅值及破坏结果分析来看,环壳与柱壳厚度比从1.225~1.675的变化过程中,虽然整体的承载能力有所提升,但破坏模式依然是环壳的失稳;当环壳与柱壳厚度比超过1.725时,才能保证结构破坏前,环壳不失稳;环壳厚度超出柱壳厚度72%、超出锥壳厚度50%时,会造成新的应力集中,因此仅从环壳加厚来提高环壳的稳定性是不合理的。
模型中环壳的稳定性问题较为突出,因此本文还研究了环壳两端3#、4#肋骨间距对模型的极限承载能力和破坏模式的影响,肋骨间距从600~700 mm之间变化,每隔100 mm取一值计算。计算结果见表3。
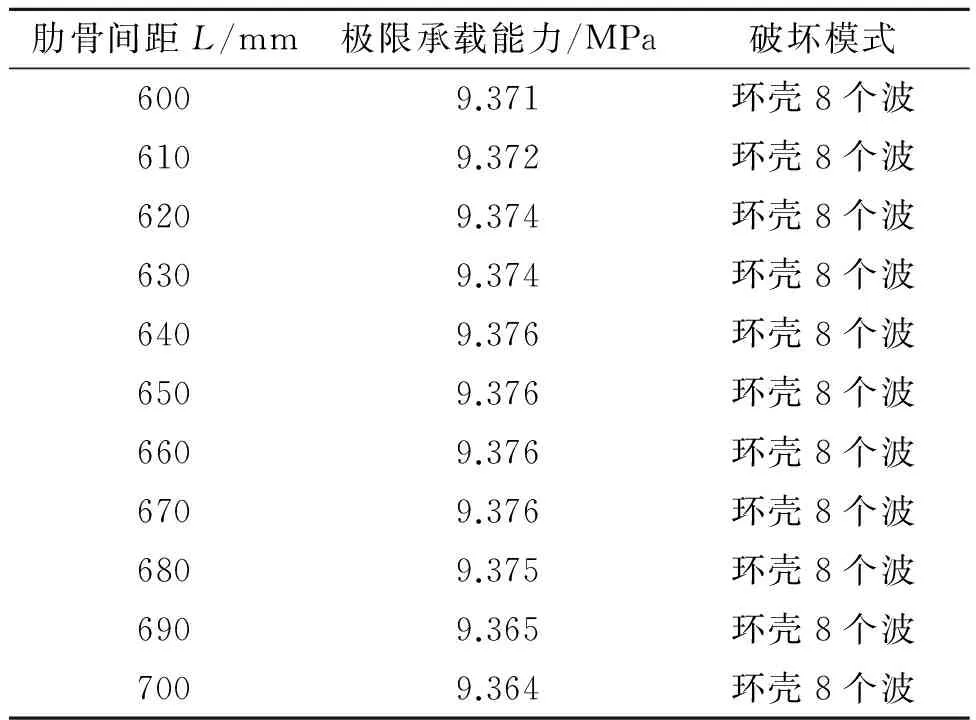
表3 不同肋骨间距下的极限承载能力和破坏模式
由表3可见,随着肋骨从600~700 mm的增加,模型的承载能力变化幅值非常小,差值不超过0.012 MPa,破坏模式均为环壳的周向失稳。从第2节破坏分析中可知,破坏是由于肋骨失稳带动壳板失稳,肋骨间距的改变无法提高肋骨的稳定。
从模型破坏结果中看到,环壳肋骨发生周向失稳,说明肋骨刚度不足,有必要将环壳的肋骨进行局部加强。肋骨原始尺寸为腹板高330 mm、厚28 mm,宽125 mm,厚35 mm。参考文献[6]中的研究方法,将肋骨尺寸调整后进行计算,见表4~表7。
从计算结果可以发现,环壳两端肋骨尺寸对加肋凹形锥环柱的极限承载能力和破坏模式有一定的影响,极限承载能力先随肋骨尺寸增加而增加,当肋骨尺寸过大时,壳板的相对承载能力就越低,极限承载能力反而有所降低,肋骨尺寸增大过
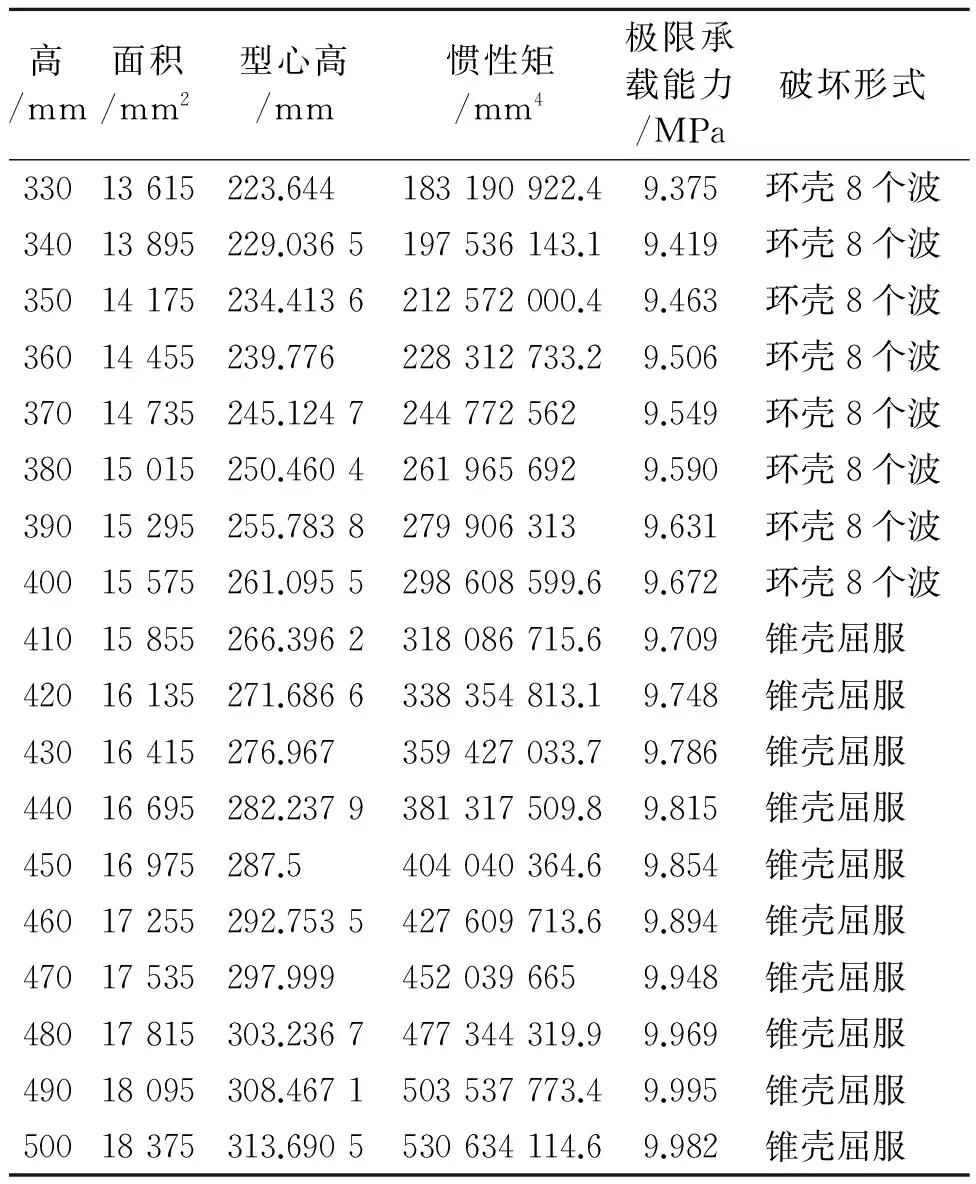
表4 不同腹板高度下的极限承载能力和破坏模式
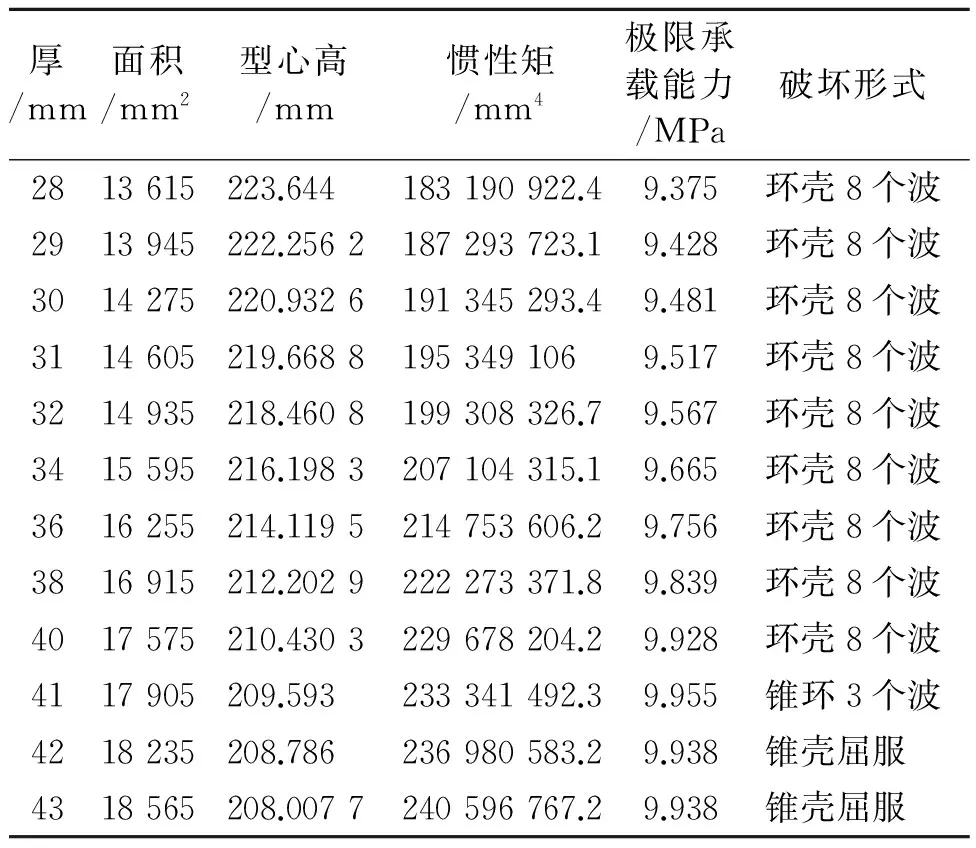
表5 不同腹板厚度下的极限承载能力和破坏模式
程中破坏模式由环壳的8个波的失稳转变为锥壳的屈服破坏,改变腹板厚度和翼板宽度过程中出现环壳与锥壳3个波整体失稳的特殊情况。
从改变肋骨尺寸幅度分析,改变肋骨的腹板高度和腹板厚度,对极限承载能力的影响大于改变翼板宽度和厚度。腹板高度增大48%、厚度增大46%时,达到极限承载能力最大值10 MPa左右,而相应腹板宽度和腹板厚度均需要增大100%才能达到同样效果。与此同时,增加腹板厚度与翼板宽度,所对应的截面积与惯性矩是最小的。
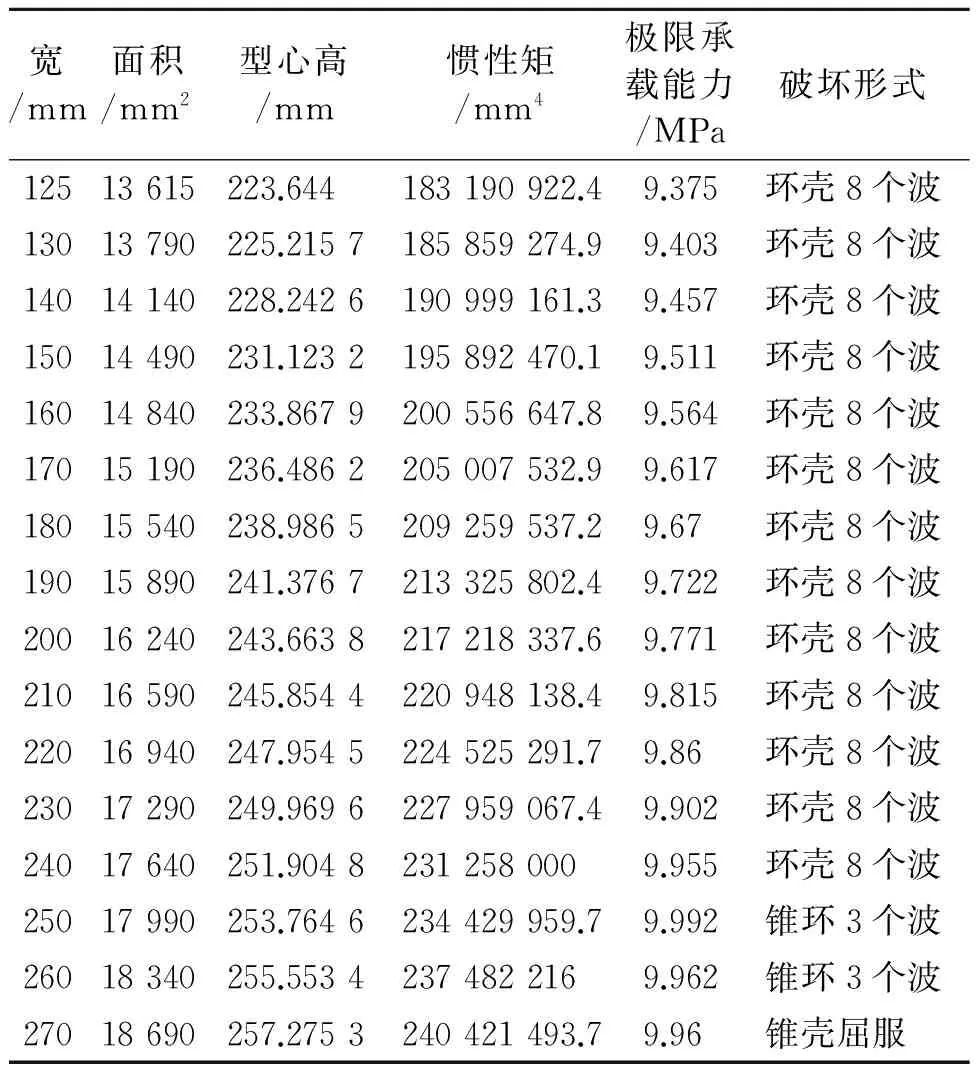
表6 不同翼板宽度下的极限承载能力和破坏模式
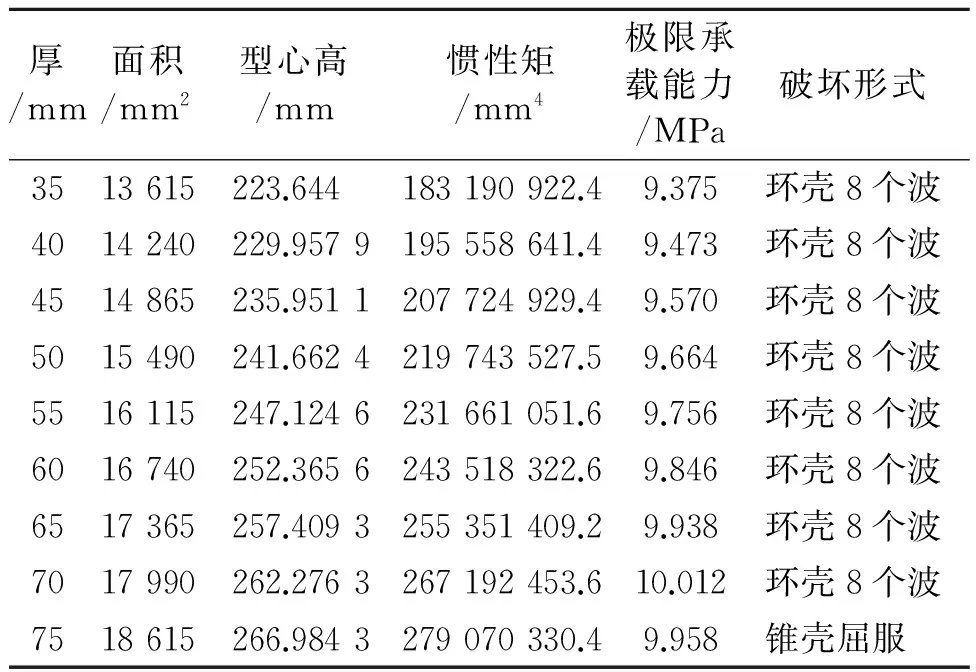
表7 不同翼板厚度下的极限承载能力和破坏模式
图5~图7为环壳失稳位移云图、整体失稳云图及锥壳失稳云图。
观察图5~图7,从参数分析中得到3种不同的破坏模式,可以发现凹形结合壳的环向应力对破坏模式起到决定作用,当环向局部加强之后,破坏模式转为锥壳屈服破坏,这与小尺寸、低屈服强度的模型试验[2]中所观测到的现象有所不同。因此,进行大尺寸、大比例下的模型研究是很有必要的。
4 结论
1)减小半锥角,增加环壳厚度,增大环壳肋骨尺寸,均能提高环壳的稳定性以及加肋凹型锥环柱的极限承载能力;改变环壳两端肋骨间距,对加肋凹型锥环柱的极限承载能力和破坏模式影响较小。
2)加肋凹型锥环柱环壳部分的环向应力较高,易出现环壳周向失稳破坏。对于结构设计而言,有必要将环壳两端肋骨进行局部加强。提高肋骨腹板尺寸,能更有效的提高整体结构的极限承载能力;增加肋骨的水平方向尺寸,能更好的提高其环壳的稳定性。
3)在提高加肋锥环柱结构环壳两端肋骨尺寸时,应避免出现整体失稳的破坏模式。
[1] 吴梵,陈昕,郭日修.加肋凹锥-环-柱结合壳结构参数分析[J].海军工程大学学报,2004,16(6):64-69.
[2] 郭日修,吕岩松.凹形加肋锥-环-柱结合壳局部加强方式研究[J].哈尔滨工程大学学报,2010,31(2):170-176.
[3] 陈志坚,郭日修.加肋轴对称壳非线分析分析方法的探讨[J].中国造船,2001,42(1):54-60.
[4] 陈志坚,郭日修.加肋轴对称壳非线稳定性分析[J].中国造船,2004,45(1):25-31.
[5] 吕岩松,郭日修.计算加肋轴对称组合壳塑性极限载荷的缩减弹性模量有限元法[J].工程力学,2014,31:171-176.
[6] 吴梵,王金,刘勇,等.几何参数对环肋圆柱壳肋骨侧向稳定性的影响[J].船舶工程,2015,10(4):59-64.
Effects of Geometric Parameters upon Ultimate Bearing Capacity of Ring-stiffened Concave Cone-toroid-cylinder Hull
MAO Kai-ren, WU Fan, ZHANG Er
(Dept. of Naval Architecture Engineering, Naval University of Engineering, Wuhan 430033, China)
The failure mechanism of the large-scaled ring-stiffened concave cone-toroid-cylinder hull under static water pressure was direct analyzed in ANSYS. The effects of geometric parameters upon ultimate bearing capacity and failure mode of the ring-stiffened concave cone-toroid-cylinder hull were studied. It was concluded that decreasing the half-cone angle, increasing the thickness of the toroid shell and the size of ribs next to the toroid shell are helpful to enhance entire structure’s ultimate bearing capacity; and increasing the ribs size in width is better to enhance the stability of the toroid shell.
ring-stiffened concave cone-toroid-cylinder hull; large scale; ultimate bearing capacity; failure mode
10.3963/j.issn.1671-7953.2017.02.005
2016-09-01
毛开仁(1992—),男,硕士,助理工程师
U661.43
A
1671-7953(2017)02-0021-05
修回日期:2016-09-23
研究方向:船舶结构强度与稳定性

