内河散货船总纵极限强度可靠性分析

邹路遥，邓乐，唐文勇

(1.上海交通大学 a.海洋工程国家重点实验室；b.高新船舶与深海开发装备协同创新中心，上海 200240；2.中国船级社 武汉规范研究所，武汉 430022；)

内河散货船总纵极限强度可靠性分析

邹路遥1，邓乐2，唐文勇1

(1.上海交通大学 a.海洋工程国家重点实验室；b.高新船舶与深海开发装备协同创新中心，上海 200240；2.中国船级社 武汉规范研究所，武汉 430022；)

针对影响内河散货船船舶结构安全的不确定因素，采用三维势流水动力程序进行波浪弯矩的长、短期预报，根据Turkstra准则选择外载荷极值组合形式，提出适用于内河散货船总纵极限强度可靠性分析方法，对某内河散货船的不同工况进行计算和分析，给出不同工况下失效概率的计算方法。

可靠性；内河船舶；总纵极限强度；不确定性因素；JC法

结构可靠性已经在船舶工业领域得到了越来越多的研究和应用。DNV于1992年发布了专门用于指导船体梁强度可靠性分析的Note30.6，并成为IACS各家船级社及学术界主要的参考资料之一[1]；IACS大力推广的协调共同结构规范(HCSR)中同样包含了可靠性理论的思想，应用结构可靠性原理进行分析，得到了极限承载能力、垂向波浪弯矩和静水弯矩的局部安全因子[2]；CCS近年来对国内钢质海船进行极限强度可靠性分析，为海船极限强度衡准公式的修订提供依据。国内许多学者也应用结构可靠性原理对船舶的极限强度、腐蚀疲劳、剩余强度等问题进行了研究[3-5]。但目前相关研究和应用仅针对海船，尚无文献针对内河船舶极限强度提出一套合适的可靠性分析方法。

在船体结构设计、建造以及运营当中，存在着许多不确定性因素，采用结构可靠性分析得到内河船总纵极限强度的可靠度指标，能更清晰反映内河船舶抵抗总纵弯曲失效的能力，并为内河船舶结构设计和相关规范的制定提供依据，以便更有效地控制内河船舶的安全水平和制造成本。

本文考虑板厚、材料、腐蚀、静水弯矩、波浪弯矩等参数的不确定性，区分航行、装卸、中垂、中拱工况，选择适合内河船舶的外载荷极值组合方法，利用改进一次二阶矩法和当量正态化(JC)法对内河船舶极限强度进行可靠性分析。

1 作用在船体上的外载荷

作用于船体梁的外载荷主要包括静水弯矩和波浪弯矩。对于内河船舶，静水弯矩是外载荷的主要成分。根据Turkstra准则，当静水弯矩为主要外载荷时，可将静水弯矩年极值和一个航次的波浪弯矩极值组合来进行可靠性分析。

1.1 静水弯矩分布和统计特征值

内河船静水弯矩的随机性主要是由于货物装载的随机性引起的，内河船在各种营运状态下，静水弯矩的随机变化近似服从正态分布[6]。具体处理时，根据装载手册或者其他资料统计散货船在航行工况和装卸工况下船中0.4 L范围内的中拱和中垂静水弯矩，从中分别选取不同工况下的最大值作为相应的静水弯矩均值：航行中垂工况变异系数选取0.10，航行中拱工况变异系数选取0(航行中拱工况一般为压载状态，舱内无货，认为静水弯矩为常数)，装卸中垂、中拱工况变异系数选取0.05。上述不同工况下的静水弯矩均值及其变异系数采用蒙特卡洛方法计算得到验证[7]。

对于原始分布为正态分布、对数正态分布等，随着样本数的增大，其极值分布都趋于极值I型分布，即Gumbel分布，因此在计算静水弯矩年极值时假设其服从Gumbel分布。

(1)

Gumbel分布参数的计算公式为

(2)

式中：f和F-1为原始分布的概率密度函数和分布函数的反函数；n为样本个数。

样本数的大小与所选取的单次航行时间、装卸时间有关，单次航行时间、装卸时间等理论上为随机变量。根据统计的平均结果，内河散货船单次航行时间设定为5 d，即1年有70多次航行工况和码头装卸工况，则静水弯矩1年的样本数可取值为70。

1.2 波浪弯矩分布和统计特征值

与海船类似，内河船舶波浪弯矩峰值的长期分布近似服从Weibull分布，单航次极值分布近似服从Gumble分布[8-9]。Weibull分布如下。

(3)

计算时根据内河船实际运营情况和内河环境设置计算参数：偏安全考虑取航速为10 kn，水深取10 m，计算频率范围为0～2 rad/s，计算浪向0°～180°(间隔15°等概率分布)，根据内河A级航区波浪散布图确定有义波高和谱峰周期的分布概率，波浪谱为JONSWAP谱，考虑短峰波的方向，分布函数取n=3[10]。在进行波浪弯矩长期预报和极值预报时，理论上应该综合考虑不同航行工况的计算结果。由于目前内河船舶不同航行工况的比例尚无可靠的数据，且内河船的满载出港工况一般为航行中的主要工况，故本文仅考虑较危险的满载航行工况，暂不考虑压载等其他工况。

随着原始样本数增大，Weibull分布的极值分布趋于Gumbel分布，即式(1)。据此认为内河船舶25年运营期间遭遇的波浪次数为108，则单航次波浪弯矩样本数n=108/25/70=57 142，将长期预报结果和的取值代入式(2)，就可以得到波浪弯矩的单航次极值分布参数。

2 极限强度的统计特征值

材料屈服极限是影响极限强度随机分布的主要不确定性因素。内河船钢材料分为高强度钢与普通碳素钢，认为这2种钢的屈服极限均服从对数正态分布，变异系数分别为0.08和0.06。常见的钢材种类和相关参数见表1。

船舶在建造过程中使用的钢板厚度也是随机变量。根据对国产钢材的调研结果，认为钢板厚度服从正态分布，所有板厚的平均值均等于名义板厚加上0.14 mm，而标准差取0.1 mm[11]。

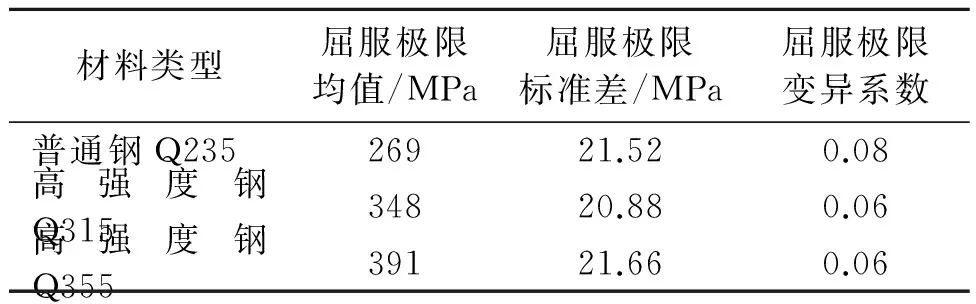
表1 钢材料相关参数

船舶在运营期间，船体构件由于腐蚀而不断变薄，极限强度也在逐渐降低。因为将腐蚀厚度作为随机变量考虑比较困难，但从安全角度出发，腐蚀减薄是不可忽视的，所以将单面腐蚀增量作为常量并按25年来考虑。参考《协调共同结构规范》(HCSR)，在对船体梁极限强度进行评估时，施加腐蚀厚度取0.5倍的腐蚀增量，即0.5tc(tc=Roundup0.5(tc1+tc2)+tres，其中tc为腐蚀增量；tc1和tc2为结构构件每侧的腐蚀增量；tres为储备厚度，取为0.5 mm)。内河船舶构件单侧的腐蚀增量见表2[12]。

表2 内河船构件单侧的腐蚀增量

考虑材料、板厚和腐蚀的影响，在未知极限强度Mu具体表达式的情况下，可以考虑采用改进Rosenblueth法计算极限强度的均值μMu和标准差σMu[13]。

3 可靠性分析原理

因为内河船舶在码头装卸货时几乎不承受波浪弯矩，所以航行工况考虑静水弯矩和波浪弯矩的组合，装卸工况仅考虑静水弯矩。

对于航行工况，极限状态方程为

(4)

式中:Mu、Msw、Mw为总纵极限强度、航行静水弯矩、航行波浪弯矩；μu、μsw、μw为对应的计算模型的不确定系数，设定为均值为1、标准差为0.1的正态分布。

对于装卸工况，不考虑波浪载荷的影响，其极限状态方程为

(5)

式中:Mu、Msw为总纵极限强度、码头静水弯矩；μu、μsw的定义和取值与航行工况相同。

建立以上极限状态方程，获得相关随机变量的统计参数，采用改进的一次二阶矩法和JC法进行可靠性分析[14]，可以得到不同工况下内河船舶极限强度的失效概率和可靠度指标。

4 算例

计算一艘内河散货船的相关统计特征并进行可靠性分析，该船的主要参数有：垂线间长Lpp=123.3 m，型深D=8.8 m，型宽B=21.8 m，方形系数Cb=0.922。船中横剖面构件布置见图1。

基于增量叠代法[15]编程并建立船中典型剖面模型，扣除腐蚀厚度，并按改进Rosenblueth方法的计算要求，修改模型中的材料屈服极限和板厚，计算出对应的极限强度，最后利用改进Ronsenblueth方法获得极限强度的均值和标准差。样本船极限强度的统计参数见表3。

表3 极限强度统计参数

统计静水弯矩数据，并根据式(2)进行静水弯矩年极值预报；采用三维势流水动力程序SESAM的Wasim模块建立湿表面水动力模型并计算波浪弯矩传递函数，接着采用其Postresp模块进行波浪弯矩长期预报，得到波浪弯矩长期分布参数，并代入式(2)得到波浪弯矩单航次极值分布参数。

航行中拱工况下静水弯矩为常数232 289.40 kN·m，其他工况下静水弯矩和波浪弯矩的极值分布参数见表4。

图2是该散货船在航行中垂工况下的静水弯矩单航次分布概率密度、年极值分布概率密度，图3是该散货船在航行中垂工况下的波浪弯矩长期分布概率密度、单航次极值分布概率密度。由图2和图3可以看出，静水弯矩集中分布在数值较大的取值区域，而波浪弯矩则集中分布在数值较小的取值区域，这与内河船舶静水弯矩大于波浪弯矩的事实相符。

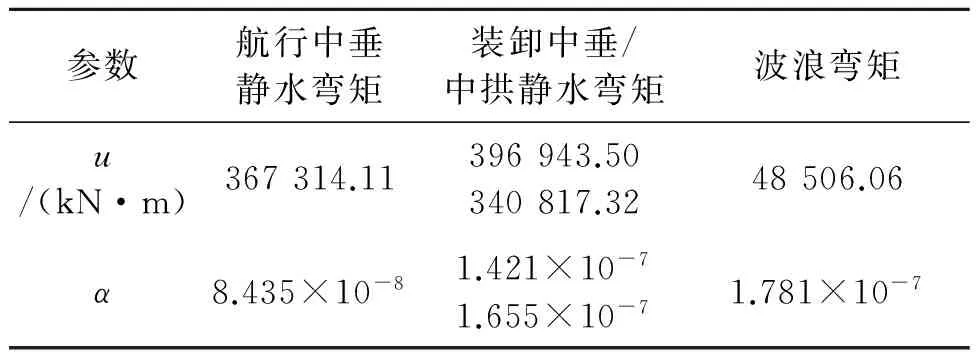
表4 外载荷极值分布参数

采用改进的一次二阶矩法和JC法进行可靠性分析，极限强度可靠性分析结果见表5。观察结果发现，与海船的目标失效概率10-3相比,该内河散货船失效概率较小，中垂工况的失效概率相比中拱工况偏大，最大失效概率接近10-4且发生在装卸中垂工况。这说明内河船舶的安全水平较高，但中垂工况仍可能是较为危险的工况，如对更多样本进行分析，则可进一步确认内河船舶总纵极限强度的安全水平。

表5 极限强度可靠性分析结果

5 结论

本文研究了内河船舶的总纵极限强度可靠性分析方法。采用适合内河船舶的外载荷极值组合方式，给出了静水弯矩和波浪弯矩极值分布的计算方法，考虑影响极限强度的不确定性因素，采用改进Rosenblueth法计算内河船舶极限强度统计特征值。在上述基础上给出了内河船舶在不同工况下失效概率的计算方法。通过计算一艘内河散货船，证明本文的方法是可行的，且能清晰地反映内河船舶抵抗总纵弯曲失效的能力。

[1] Det Norske Veritas. Classification notes No.30.6[S]. Norway: Det Norske Veritas,1991.

[2] IACS. Common Structural Rules for Double Hull Oil Tankers, Background Document[S]. IACS,2006.

[3] 何福志,万正权.基于船体结构总纵极限强度的可靠性分析[J].船舶力学,2002,6(2):27-45.

[4] 闫小顺,黄小平.基于改进裂纹扩展模型的船舶焊接结构疲劳寿命可靠性预报[J].上海交通大学学报,2015,49(2):215-219.

[5] 任慧龙,李陈峰.破损舰船剩余强度的可靠性评估方法研究[J].船舶力学,2010,14(7):758-764.

[6] 王杰德,张怀宇.内河船舶静水弯矩的统计分析[R].武汉交通科技大学内河船舶强度标准研究报告,1997.

[7] 郭昌捷.船体梁静水弯矩的统计分析[J].大连理工大学学报,1990,01:73-79.

[8] 王杰德,张怀宇.关于船体波浪弯矩极值分布的近似分布规律的研究[J].武汉交通科技大学学报,1998,22(1):27-29.

[9] 王杰德,赵金霞.内河船舶总纵强度安全指标与安全系数的研究[J].武汉理工大学学报(交通科学与工程版),2003,27(1):15-17.

[10] 陈钰,邓乐,唐文勇.内河船舶可靠性分析中的波浪弯矩统计与极值分布[J].船舶工程,2016,38(6):6-9.

[11] 中国船级社.船体梁极限强度可靠性研究—板厚与材料参数统计及影响分析报告[R].北京：中国船级社，2013.

[12] 中国船级社.内河船舶结构腐蚀研究[R].北京：中国船级社，2014.

[13] 崔维成,徐向东,邱强.一种快速计算随机变量函数均值与标准差的新方法[J].船舶力学,1998,2(6):50-59.

[14] 吴世伟.结构可靠性分析[M].北京:人民交通出版社,1990.

[15] 中国船级社.钢质内河船舶入级规范[M].北京:人民交通出版社,2015.

Reliability Analysis of Ultimate Strength of Inland Waterway Bulk Carriers

ZOU Lu-yao1, DENG Le2, TANG Wen-yong1

(1 a.State Key Laboratory of Ocean Engineering; b.Collaborative Innovation Center for Advanced Ship and Deep-sea Exploration, Shanghai 200240, China;2.Wuhan Rule and Regulation Research Institute, China Classification Society, Wuhan 430022, China)

According to various uncertainties affecting the structural safety of ships, the short-term and long-term forecasts for wave bending moment were calculated based on the 3D wave loads theory. The combination method of extreme external loads was chosen by Turkstra’s principle. A suitable reliability analysis method including calculation of the failure probability in different operation conditions for inland waterway ships was proposed. A numerical example was given.

reliability; inland waterway ships; longitudinal ultimate strength; uncertainties; JC method

10.3963/j.issn.1671-7953.2017.02.007

2016-08-02

工信部项目(工信部联装〔2016〕26号)

邹路遥(1992—)，男，硕士生

U661.43

A

1671-7953(2017)02-0030-04

修回日期：2016-08-23

研究方向:船舶结构可靠性分析