某复杂大跨火车站风致响应分析
陈 卓 曾加东
(1.西南交通大学风工程实验研究中心,四川 成都 611031; 2.风工程四川省重点实验室,四川 成都 611756)
某复杂大跨火车站风致响应分析
陈 卓1曾加东2
(1.西南交通大学风工程实验研究中心,四川 成都 611031; 2.风工程四川省重点实验室,四川 成都 611756)
针对某复杂大跨火车站屋盖结构风致振动问题,采用频域法中考虑模态耦合效应的分量法,求解了结构在风荷载下的响应,结果表明,采用改进的分量法求解大跨屋盖结构的风振系数具有较高的精度,可满足工程计算的要求。
大跨屋盖,风振系数,分量法,时程分析,风洞实验
0 引言
近年来,为了满足功能和外形的需要,大型火车站越来越多地采用大跨屋盖结构形式。大跨屋盖结构具有质量轻、柔度大、阻尼小、自振频率低、振型密集等特点,导致其风荷载作用敏感,风荷载已成为大跨屋盖结构的主要设计荷载之一[1-3]。然而在现行建筑结构荷载规范[4]中,大跨度屋盖结构的风振系数的选取带有较大的经验性。对于重要且体型复杂的房屋和构筑物,为确保结构的抗风安全,需利用刚性模型测压风洞实验,研究作用于建筑物上的风荷载及风致振动特性。
本文以某大型火车站这一实际工程结构为例,介绍了计算大跨屋盖位移风振系数方法。采用频域法中考虑模态耦合效应的分量求解法和时程分析法求解结构在风荷载作用下的响应,得到了大跨度火车站屋盖在各个风向角下的脉动响应。不仅能为结构设计提供依据,也可对类似建筑结构风荷载作用研究提供了一定的参考价值。
1 大跨度屋盖结构风振响应理论分析
1.1 结构风振响应的分析方法
对大跨屋盖结构风致振动的分析可分为时域分析法和频域分析法两类。频域法由于其概念清晰、计算效率高,方法简单可靠,在工程实践中有更为广阔的应用前景。频域法一般采用模态叠加法和分量法。
模态叠加法的基本方法是CQC法和SRSS法。CQC法精度较高,但效率较低,而SRSS法忽略了模态之间的耦合项,精度较低。同时模态叠加法还需要考虑参振模态的选取,而将风振响应分为背景响应和共振响应进行分析,不仅能够克服模态叠加法的不足,并且能够较好地解释风荷载对结构作用的机理,因此在国内外风工程研究中得到了广泛应用[5,6]。但传统的分量法将共振响应和背景响应采用SRSS方法进行组合,忽略了模态耦合项,并且分析共振响应时仍存在高阶模态截断误差。国内外众多学者对其进行了分析与改进。
沈国辉等[7]比较了模态叠加法与分量法之间的联系和区别,认为对于风致响应两种方法得到的结果一致。
Huang G[8]则提出结构的背景响应采用所有的模态,共振响应则采用白噪声的简化方法,并引入了共振响应各阶模态广义力之间的实部相关系数表达式。
柯世堂等[9]采用随机振动的方法推导了背景和共振以及二者之间的耦合项的计算公式,并以实际工程结构为例证明其方法具有较高精度。
本文在此基础上,从模态加速度法出发,介绍考虑模态耦合效应的分量求解法。
1.2 考虑模态耦合效应的分量求解法[10,11]
对于自由度数为n的多自由度体系,动态位移可用结构的全部振型表示为:
(1)
其中,φj为第j阶振型向量;qj,b(t)为仅包含准静力贡献的第j阶背景模态响应向量;qj,r(t)为仅包含共振效应贡献的第j阶共振模态响应向量;{y(t)}b,n为包含所有模态准静力贡献的背景位移响应向量;{y(t)}r,m为前m阶主要贡献振型的位移。
根据式(1),{y(t)}的互相关函数为:
(2)
其中,Ryy(τ)为动态位移的互相关函数;Rybyb(τ)为位移背景分量的互相关函数;Rybyr(τ)为位移背景分量与共振分量的互相关函数;Ryryb(τ)为位移共振分量与背景分量的互相关函数;Ryryr(τ)为位移共振分量的互相关函数。
两边进行傅里叶变换,得:
Syy(ω)=Sybyb(ω)+Sybyr(ω)+Syryb(ω)+Syryr(ω)
(3)
其中,Syy(ω)为动态位移的互谱函数;Sybyb(ω)为位移背景分量的互谱函数;Sybyr(ω)为位移背景分量与共振分量的互谱函数;Syryb(ω)为位移共振分量与背景分量的互谱函数;Syryr(ω)为位移共振分量的互谱函数。
对式(3)积分,根据式(1),并由轮换对称性,均方根响应可表示为:
(4)
其中,σy为脉动风总位移向量{y(t)}的均方差;σb为背景响应的均方差;σr为共振响应的均方差;σb,r为背景响应与共振响应间的耦合项;ρb,r为背景响应和共振响应间的相关系数。
实际结构在设计时,并不直接使用屋盖各点在脉动风作用下的位移均方差,而是采用风振系数计算风荷载:
(5)

2 工程实例分析
2.1 风洞实验简介及结构振型分析
某大型火车站长304 m,宽208 m,高40 m,空间尺度较大。为确保结构的抗风安全,需进行刚性模型测压风洞实验,研究作用于建筑物上的风荷载及风致振动特性。风压实验在西南交通大学风工程实验研究中心XNJD-3工业风洞中进行。该风洞目前是世界上最大的工业风洞。模型的几何缩尺比取为1∶100,按几何外形相似要求,采用金属管材、复合材料、有机玻璃等制成。大气边界层属B类地区,模拟装置由挡板、尖塔、粗糙元组成,风洞中的实验模型如图1所示。

本次风洞实验采用同步脉动压力测量系统,测试了屋盖表面共2 010个测点的风压时程。对节点风荷载时程进行适当变换,可获得广义模态力谱矩阵。同时建立有限元模型,采用时程分析法计算了结构的风振响应,以用于和频域法计算结果的对比。
2.2 风振响应计算
采用频域法中考虑模态耦合效应的分量求解法和时程分析法求解了结构在风荷载下的响应,提取典型节点的脉动位移根方差,见表1。应当指出,风向角工况较多,考虑到篇幅,本文仅选取45°风向角的结果为例。
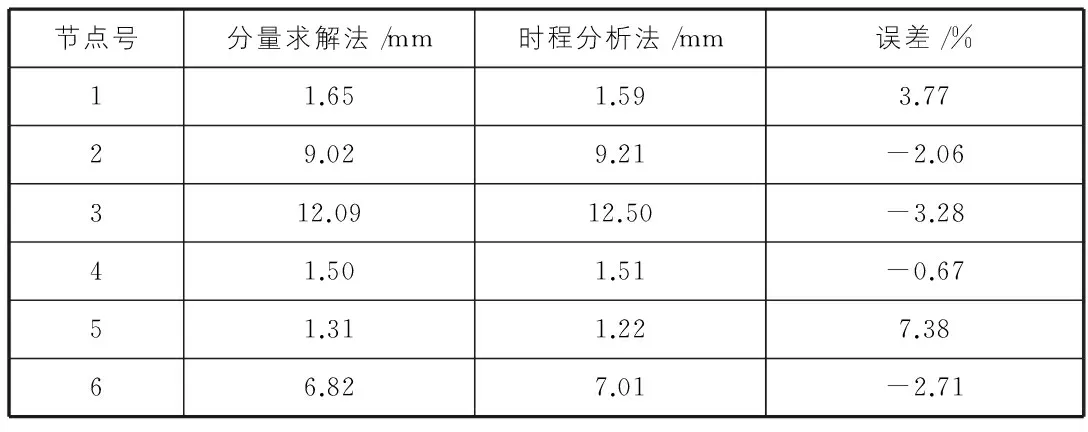
表1 典型节点脉动响应均方差
从表1中可以看出分量求解法和时程分析法两种算法结果较为吻合,相对误差较小(10%以内),可见考虑模态耦合效应的分量求解法具有较高的精度,故可以用来计算大跨屋盖结构风振系数。
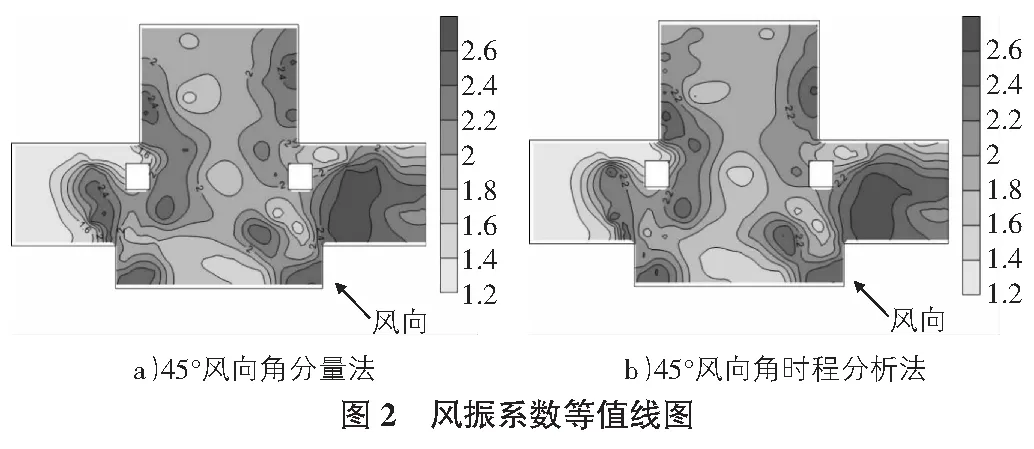
由于本火车站屋盖主要以竖向振动为主,故只对其竖向响应进行分析,对0°,45°,90°,135°,180°,225°,270°,315°等8个风向角下的竖向位移风振系数进行了分析。由于屋盖面积较大,分区较多,为方便观察与工程应用,做出各风向角下风振系数的等值线图。图2为45°风向角下频域和时域两种算法求得的风振系数等值线图。
从图2中可以看出:考虑模态耦合效应的分量求解法和时程分析法两种算法求得的风振系数在屋盖上的分布几乎一致,大部分地方风振系数相对误差在10%以内,满足工程精度。说明可以用频域内改进的分量法代替时程分析法求解大跨屋盖结构的风振系数。
同时可以看出,本火车站大跨屋盖结构竖向位移风振系数在1.22~2.63的范围内变化,背风区屋檐风振系数较小,屋盖中心区域风振系数较一致。
3 结语
通过对某大型火车站风洞实验,采用频域法中考虑模态耦合效应的分量求解法进行了风振系数的计算分析,可以得出以下结论:
1)采用频域法中考虑模态耦合效应的分量求解法和时程分析法求解结构在风荷载下的响应,提取典型节点的脉动位移根方差进行对比,两种算法结果相对误差较小。说明采用频域内改进的分量法求解大跨屋盖结构的风振系数具有较高的精度,可满足工程计算的要求。
2)风荷载是大跨屋盖结构的控制荷载,需进行风洞实验加以分析。
本文采用改进的分量法分析了某火车屋盖的位移风振系数,其竖向位移风振系数在1.22~2.63的范围内变化。
[1] 张相庭.结构风压和风振计算[M].上海:同济大学出版社,1985.
[2] Yasui H,Marukawa H,Katagiri J,et al.Study of wind-induced response of long-span structure[J].Journal of Wind Engineering & Industrial Aerodynamics,1999,83(1):277-288.
[3] 田玉基,杨庆山.国家体育场屋盖结构的风振响应特点[J].土木工程学报,2010(6):1-7.
[4] GB 50009—2012,建筑结构荷载规范[S].
[5] Zhou Y,Kareem A.Gust loading factor:New model[J].Journal of Structural Engineering,2001,127(2):168-175.
[6] Holmes J D.Effective static load distributions in wind engineering[J].Journal of Wind Engineering & Industrial Aerodynamics,2002,90(2):91-109.
[7] 沈国辉,孙炳楠,楼文娟.屋盖结构背景响应等效风荷载的一种简化算法[J].工程力学,2006,23(S1):163-168.
[8] Huang G,Chen X.Wind load effects and quivalent static wind loads of tall buildings based on synchronous pressure measurements[J].Engineering Structures,2007,29(10):2641-2653.
[9] 柯世堂,葛耀君.基于一致耦合法某大型博物馆结构风致响应精细化研究[J].建筑结构学报,2012,33(3):111-117.
[10] 陈 波.大跨屋盖结构等效静风荷载精细化理论研究[D].哈尔滨:哈尔滨工业大学,2006.
[11] 罗 楠.大跨屋盖结构风致振动分析及等效静力风荷载研究[D].成都:西南交通大学,2012.
Study of wind-induced vibration response on long span roof of a railway station
Chen Zhuo1Zeng Jiadong2
(1.ResearchCenterforWindEngineering,SouthwestJiaotongUniversity,Chengdu611031,China;2.WindEngineeringKeyLaboratoryofSichuanProvince,Chengdu611756,China)
Aiming at the wind-induced vibration of the long span roof, a three-component procedure which considers the coupling effect is proposed to obtain the response of structure on wind loads. The results show that the three-component procedure can work out the wind vibration coefficient sufficiently and meet the requirements of engineering calculation.
long-span roof structure, wind vibration coefficient, component method, time domain analysis, wind tunnel test
1009-6825(2017)10-0057-03
2017-01-23
陈 卓(1991- ),男,在读硕士
TU391
A

