基于DEA模型的皖北各市R&D效率研究
李少付,张 娜
(蚌埠学院 经济与管理系,安徽 蚌埠 233000)
基于DEA模型的皖北各市R&D效率研究
李少付,张 娜
(蚌埠学院 经济与管理系,安徽 蚌埠 233000)
以2010~2014年皖北六市R&D投入与产出数据为样本,利用DEA模型测算了样本的整体效率、技术效率、规模效率和规模收益;通过建立包含时期影响的固定效应变截距模型检验了R&D经费投入强度对整体效率的影响是否显著。研究发现:皖北六市R&D投入与产出水平较低,研发整体效率具有显著的空间异质性,在2010~2014年期间皖北地区研发整体效率表现为逐年上升的趋势,R&D经费投入强度对整体效率具有显著的负面影响。
DEA模型;R&D经费投入强度;固定效应模型
0 引言
我国经济的驱动方式正在从要素驱动向创新驱动转变,创新驱动将是未来经济发展的关键推动力。《“十三五”国家科技创新规划》强调,坚持创新是引领发展的第一动力,以深入实施创新驱动发展战略、支撑供给侧结构性改革为主线,大力推进以科技创新为核心的全面创新,塑造更多依靠创新驱动、更多发挥先发优势的引领型发展,确保如期进入创新型国家行列,为建成世界科技强国奠定坚实基础。
皖北地区包括淮北市、亳州市、宿州市、蚌埠市、阜阳市和淮南市。表1显示了皖北地区2014年R&D投入产出情况。R&D人员折合全时当量投入除了蚌埠市为8 384人年,略高于全省平均水平的8 082人年,淮南市为7 098人年,略低于全省平均外,其余各市均大幅低于全省平均水平;淮北市和蚌埠市R&D资本投入(用科研用仪器设备原价表示)分别为231 234万元和246 728万元,高于省平均值189 995万元,其余各市均低于省平均水平;R&D经费投入除了蚌埠市为234 059万元,略低于全省平均水平的246 004万元,其余均大幅低于全省平均水平;R&D经费投入强度(R&D经费投入占GDP的百分比)只有蚌埠市和淮南市为2.03%,高于全省平均水平的1.89%,其余均较大幅度低于全省平均水平;各市的新产品销售收入均不同程度地低于全省平均水平的3 300 551万元;新产品销售收入占GDP的百分比除了蚌埠市为24.99%,略低于全省平均水平外,其余各市均大幅低于全省平均水平;各市的专利申请数均不同程度地低于全省平均水平。
综上分析,皖北六市2014年研发创新投入与产出水平较低,且内部差异显著。研发创新的产出水平较低既有可能是由于较低的投入水平所致,也有可能是由于较低的研发效率引起。皖北地区经济发展水平较低,靠增加投入提高研发创新水平和能力空间有限,提高R&D效率尤其重要。
目前国内学术界对决策单元研发效率的研究方法主要有参数与非参数两大类。参数方法以随机前沿分析(Stochastic Frontier Analysis,SFA)方法为代表,SFA 采用计量方法对前沿生产函数进行估计,通过估计生产函数对生产过程进行描述,从而测算每个决策单元的技术效率。SPF方法的优点是不仅可以测算每个决策单元的技术效率,而且可以根据经济理论定量分析各种相关因素对决策单元技术效率差异的具体影响。然而SPF方法也存在一定的缺点:一是要求设定具体的生产函数,对决策单元技术效率的测评结果依赖于生产函数的选择。二是SPF只能处理单一产出的情况,使得对研发创新活动技术效率的衡量不够全面。

表1 皖北地区2014年R&D投入产出情况
资料来源:根据2015年《安徽省统计年鉴》计算整理。
非参数统计分析方法以数据包络分析(data envelopment analysis,简称DEA)为代表,DEA是1978年由美国运筹学家A.Charnes,W.W.Cooper and E.Rhodes首先提出[1]。它是根据一组关于投入/产出的观测值来估计有效生产前沿面(efficient production possibility surface)。DEA可用线性规划来建模、求解及判断决策单元对应的点是否位于有效生产前沿面上,不需要考虑指标的纲量,无需设定生产函数的具体形式,从而避免了主观设定函数形式的影响。徐磊等基于2004~2012年间全国31个省份的面板数据,同时使用随机前沿分析法及数据包络分析法,实证分析了中国各区域研发投入产出的效率,研究发现两种方法所得效率值之间存在着显著正相关关系[2];代明等利用双前沿面数据包络法,测量了中国高技术产业的乐观效率和悲观效率,并用两者的几何平均效率表示综合效率[3];冯志军等将高技术产业研发创新过程分解为技术开发和经济转化两个前后相续的子阶段,构建了资源约束型两阶段DEA模型,实证测评了中国高技术产业17个细分行业研发创新的整体及各子阶段的效率[4]。
本文利用DEA模型对皖北各市R&D效率进行测量与评价。与以往的研究相比,本文在以下两个方面进行了探索:第一,以科研用仪器设备原价作为研发创新存量资本投入,以研究与实验发展经费作为研发创新流动资金和维持运营资本投入。白俊红等认为应选用R&D资本存量[5],而非R&D经费支出这一流量指标,并用永续盘存法来核算R&D资本存量,计算公式为Kit=(1-δ)Ki(t-1)+Eit,即以第t-1期资本存量扣除折旧,加上第t期实际R&D 经费支出作为第t期资本存量。这种处理方法并不准确,根据统计年鉴指标解释,R&D经费支出包括用于R&D项目活动的直接支出,以及间接用于R&D活动的管理费、服务费、与R&D有关的基本建设支出以及外协加工费等,按用途划分可分为日常性支出与资产性支出。总之,实际R&D 经费支出并没有全部转化存量资本,存量资本与流量支出作为研发创新活动的两项投入不可替代,两者不可或缺。第二,在对研发效率测量结果观察分析时发现,研发经费投入强度高的蚌埠市和淮南市研发整体效率反而较低,而投入强度适中的淮北市研发整体效率最低,于是提出“研发经费投入强度对研发整体效率具有显著负面影响”的假设,通过建立包含时期影响的固定效应变截距模型证实了假设的正确性。
1 DEA模型
数据包络分析模型包括投入型与产出型两种类型,由于投入资源的稀缺性和可控性,本文以投入型DEA作为分析模型。
1.1 评价生产效率的DEA-CCR模型
设参照集为
其中,xj=(x1j,x2j,…,xmj)T,j=1,2,…,n为m维投入向量;yj=(y1j,y2j,…,ysj)T,j=1,2,…,n为s维产出向量。
在满足平凡性、凸型、锥性、无效性和最小性公理体系下[6](P39-46),可以唯一地确定投入DEA-CCR模型的生产可能集
相应的DEA-CCR模型为
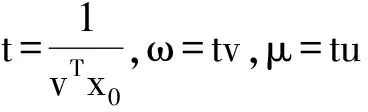
它的对偶规划为
上述对偶形式CCR模型的经济含义比较容易理解:判断决策单元j0相对于其他决策单元是否有效就是观察在产出不减少的约束下,投入可以缩减的最大比例(即最小的θ)。然而,求解上述模型并非易事。为了有效利用单纯形法求解以及对求解结果分析的方便,应用中通常使用下面带有非阿基米德无穷小量的模型。
其中,xij:第j个决策单元对第i种类型投入的投入量,xij>0,为已知数据;
yrj:第j个决策单元对第r种类型产出的产出量,yrj>0,为已知数据;



(1)若θ0=1,s0-=0,s0+=0,则决策单元j0为DEA有效。
此时在原投入量基础上得到的产出量已达最优,既不存在投入剩余,即(1-θ0)x0+s0-=0,也不存在产出亏空,即s0+=0。

因为这时虽径向移动等于0,即(1-θ0)x0=0,但或存在投入剩余,或存在产出亏空,或两者都存在。
(3)若θ0<1,则决策单元j0不为弱DEA有效。
DEA-CCR模型求解的是决策单元的整体效率,使用该模型进行效率评价时,是同时对技术效率和规模效率进行评价,DEA-CCR模型不能单纯评价决策单元的技术有效性。
1.2 评价技术效率的DEA-BCC模型
由于DEA-CCR模型不能单纯评价决策单元的技术有效性,1984年Banker,Charnes和Cooper给出了DEA-BBC模型[7],可以单纯地评价决策单元的技术有效性。


1.3 评价规模收益的DEA-FG,ST模型
DEA-FG模型是1985年由Fare和Grosskopf首先提出,其不仅可以评价决策单元的技术有效性,而且可以判断决策单元或为规模收益不变或为规模收益递减。DEA-ST模型是1990年由Seiford和Thrall首先提出,其既可以评价决策单元的技术有效性,也可以判断决策单元或为规模收益不变或为规模收益递增。
与DEA-BBC模型相比,DEA-FG模型公理体系中多了压缩性假设,DEA-ST模型多了扩张性假设。相应地DEA-FG模型和DEA-ST模型的生产可能集分别为:
2 实证分析
2.1 变量与数据
数据包络分析模型需要设定投入变量和产出变量,投入变量主要包括人员投入与资金设备投入。参照白俊红等的研究,本文选取R&D人员折合全时当量表示人员投入,其值为报告年内R&D全时人员数加非全时人员按工作量折算成全时人员数的总和[8];选取R&D经费投入与科研用仪器设备原价代表资金设备投入,选取的原因引言中已有分析,这里不再赘述。
产出变量主要包括知识产出和经济产出。有关知识产出的代表变量有的学者认为专利申请数较为理想,如冯志军[4]等;有的学者选取专利授权数,如项本武[9]。专利授权数的优点是能更好地反映知识产出的质量,但专利授权滞后于专利申请1~2年,所以本文选取专利申请数作为知识产出的代表。关于经济产出的代表,本文选取新产品销售收入表示,该指标在应用研究中被广泛采用。
本文以皖北六市2010~2014年研发投入、产出数据作为参考集,利用DEA模型评价决策单元期间R&D活动的相对效率,所有数据来源于2011~2015年安徽省统计年鉴,其中2014年数据已整理在表1中。
2.2 模型求解与结果分析
2.2.1 模型求解
利用MaxDEA软件求解,求解结果整理于表2中。
2.2.2 结果分析
观察表2的特点,可根据R&D经费投入强度将皖北6市分为3类:{蚌埠市、淮南市},{淮北市},{亳州市、宿州市、阜阳市}。以2014年为例,蚌埠市与淮南市的R&D经费投入强度均为2.03%,高于全省平均的1.89%;淮北市R&D经费投入强度为1.20%,水平适中;亳州市、宿州市与阜阳市R&D经费投入强度分别为0.39%、0.33%、0.51%,处于较低水平。
首先,淮南市的整体效率、技术效率、规模效率和规模收益从2012年开始均表现出与蚌埠市相同的特点,这里仅以蚌埠市展开分析。蚌埠市的整体效率从2010年的0.840 478缓步下降至2014的0.737 092,而技术效率却呈上升趋势,其中2012~2014年均为DEA技术有效。由整体效率的分解式(见本文第二部分)可知,蚌埠市期间整体效率下降的主要原因是规模效率的下降,期间规模收益均为递减状态,即产出扩张的比例小于投入扩张的比例。
为进一步深入了解产出剩余和产出亏空情况,将蚌埠市2010~2014年DEA-CCR模型求解的变量取值情况列于表3中。以2014年为例,投入方面:人员投入存在2 467人年的剩余,全部为径向移动,没有人员闲置;科研用设备投入剩余为124 530万元,其中64 867万元为径向移动距离,表示相对于其他有效决策单元,科研用设备可以缩减的最大值,59 663万元为偏差变量取值,表示处于闲置状态的资源价值;经费投入存在61 536万元剩余,全部为径向移动。产出方面:新产品销售收入不存在产出亏空,专利申请数有394件产出亏空。
其次,淮北市整体效率具有以下特点:第一,逐年上升,从2010年的0.127 805逐年上升至0.472 529;第二,水平较低,2014年整体效率仅为0.472 529,模型求解结果显示径向移动距离和各投入变量的偏差变量均较大,从而导致较大的投入剩余,新产品销售收入和专利申请数均不存在产出亏空;第三,整体效率水平较低的原因由技术效率和规模效率共同所致,并主要由技术效率低下所引起;第四,各年规模收益均递增,结合投入剩余较大、不存在产出亏空的情况,说明对于淮北市来说,缩减研发规模在经济上是有益的。
最后,亳州市、宿州市、阜阳市的整体效率、技术效率、规模效率基本上处于上升趋势,并在2014年达到DEA有效,投入剩余和产出亏空都为0,规模收益不变。
2.3 R&D经费投入强度对整体效率的影响
本文在引言中指出,研发创新的产出水平较低既有可能是由于较低的投入水平所致,也有可能是由于较低的研发效率引起。《“十三五”国家科技创新规划》提出到2020年R&D经费投入强度达到2.5%的战略目标,检验“R&D经费投入强度对整体效率的影响是否显著”假说具有重要的现实意义。下面通过建立面板数据模型对上述假设进行检验,因为面板数据模型有三种形式,关于模型的设定做三点说明:首先,因为我们的样本包括了总体中所有的个体,因此选择固定效应模型;第二,总体中的六个个体处于同一区域,假设R&D经费投入强度对整体效率的影响是相同的,据此选择变截距模型;第三,在变截距中同时包含截面个体的空间异质性和跨时期的变化[10](P319-338)。基于此,本文选择包含时期影响的固定效应变截距模型。

表2 皖北地区2010~2014年R&D效率
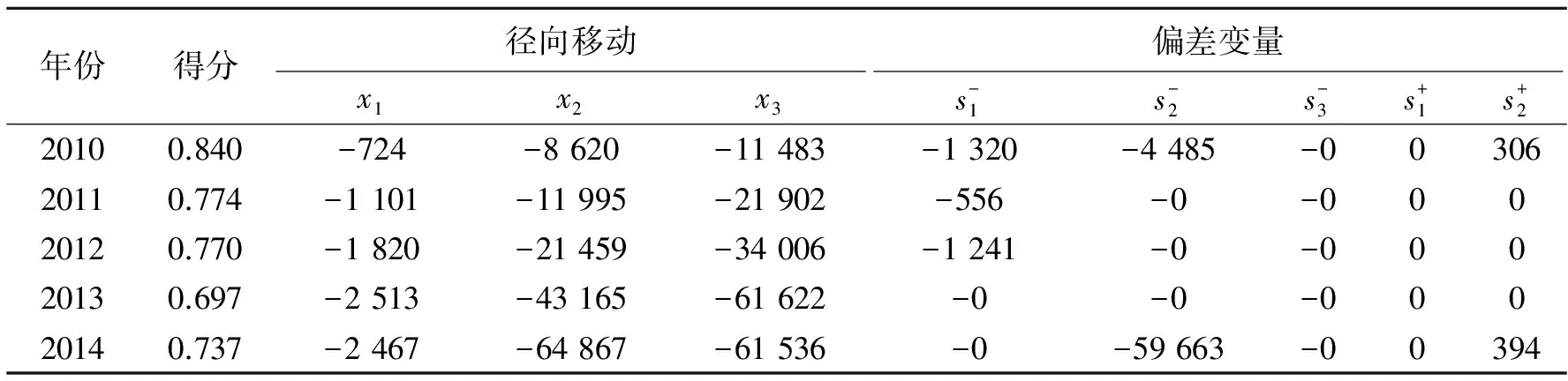
表3 蚌埠市2010~2014年DEA-CCR模型求解有关变量取值情况
说明:表中的x1,x2,x3分别表示R&D人员投入,科研用设备投入,经费投入。因为是投入DEA模型,产出变量的径向移动为0,表中没有给出。
其中,θit表示第i个城市在第t年的整体效率,inputit表示第i个城市在第t年R&D经费投入强度,D2011,…,D2014表示时期虚拟变量,比如D2011:当样本在2011年取值时等于1,其余等于0,其他类似;DBZ,…,DHN为截面个体虚拟变量,比如DBZ:当样本在亳州市取值时等于1,其余等于0,其他类似。注意为避免“虚拟变量陷阱”,时期虚拟变量设置了4个,选择2010年作为基准时期,系数α1,…,α4的含义为皖北六市研发整体效率在2011,…,2014的平均值相对于2010年的偏离;同样截面个体虚拟变量设置了5个,选择淮北市为基准个体,系数γ1,…,γ5的含义为亳州市、宿州市、蚌埠市、阜阳市、淮南市的研发整体效率在2010~2014年的平均值相对于淮北市的偏离[11](P490-498)。
以皖北六市2010~2014年数据为样本,利用Eviews 6.0软件及普通最小二乘法对模型进行估计,结果如表4所示。
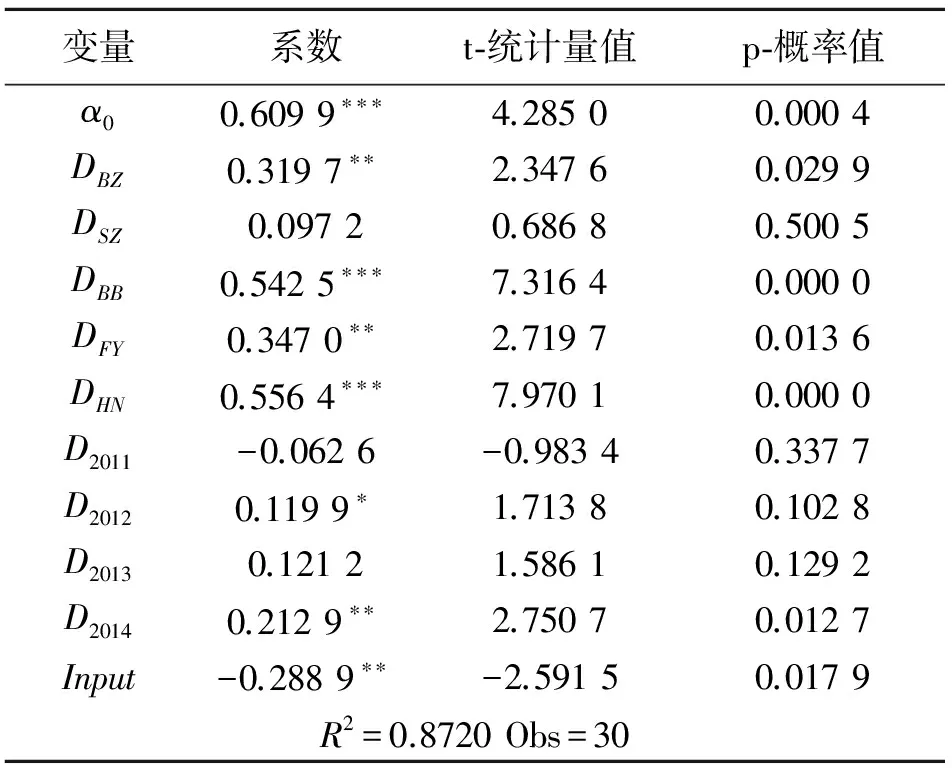
表4 含时期影响的固定效应变截距模型估计结果
说明:*,**,***分别表示在10%,5%,1%的水平上显著。
由表4可知模型的拟合优度为0.872 0,模型中的变量较好地反映了R&D整体效率的变异,同时也说明了模型设定的合理性。根据模型估计结果可总结三点结论:第一,在控制了时间变化和投入强度变化之后,皖北六市研发整体效率由强到弱的排序为:淮南、蚌埠、阜阳、亳州、宿州和淮北,注意这里的排序与DEA模型的排序结果表现的差异:{蚌埠市、淮南市}排在了{亳州市、宿州市、阜阳市}的前面,其主要原因在于面板数据模型控制了R&D经费投入强度的变化,而DEA模型则没有。第二,在2010~2014期间,皖北地区研发整体效率表现为逐年上升的趋势(只在2011年出现轻微下降且不显著)。第三,R&D经费投入强度对整体效率具有显著的负面影响。
3 总结
本文在引言中通过对皖北地区2014年研发活动的投入和产出现状与全省平均水平进行了对比分析,发现皖北六市2014年研发投入与产出水平较低,且内部差异显著。在第二部分对DEA模型的相关概念和基本原理做了概要的总结和梳理,为模型求解结果的分析奠定了基础。第三部分利用DEA模型测算了皖北六市2010~2014年间R&D活动的整体效率、技术效率、规模效率和规模收益,结合模型变量值对求解结果展开了较为详细的分析。最后通过建立包含时期影响的固定效应变截距模型对皖北地区R&D整体效率的空间异质性、时间演化趋势及R&D经费投入强度对整体效率的影响进行了研究,发现R&D经费投入强度对整体效率具有显著的负面影响。“R&D经费投入强度对整体效率具有显著的负面效应”具有较强的政策意义,该结论在样本以外的其他区域、其他时期是否存在,影响的机理是什么留待后续研究。
[1]A.Charnes, W.W.Cooper and E.Rhodes. Measuring the Efficiency of Decision Making Units[J]. European Journal of Operational Research,1978(2):429-444.
[2]徐磊,周帆.我国区域研发投入产出有效性研究[J].云南财经大学学报,2015(1):92-98.
[3]代明,刘可新,陈俊.中国高技术产业研发创新效率研究[J].中国科技论坛,2016(1):5-10.
[4]冯志军,陈伟.中国高技术产业研发创新效率研究——基于资源约束型两阶段DEA模型的新视角[J].系统工程理论与实践,2014(5):1202-1212.
[5]白俊红,江可申,李婧.应用随机前沿模型评测中国区域研发创新效率[J].管理世界,2009(10):51-61.
[6]魏权龄.评价相对有效性的数据包络分析模型[M].北京:中国人民大学出版社,2012.
[7]R. D. Banker, A. Charnes and W. W. Cooper. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis[J].Management Science,1984, 30(9): 1078-1092.
[8]白俊红,江可申,李婧.中国区域创新系统创新效率综合评价及分析[J].管理评论,2009(9):3-9.
[9]项本武.中国工业行业技术创新效率研究[J].科研管理,2011(1):10-14.
[10]高铁梅.计量经济分析方法与建模(第二版)[M].北京:清华大学出版社,2009.
[11]Chris Brooks. Introduction Econometrics for Finance(second edition)[M].Cambridge University Press, 2008.
Research on the R&D Efficiency of Different Northern Citiesin Anhui Province Based on DEA Model
LI Shaofu, ZHANG Na
(Economics&ManagementCollege,BengbuUniversity,Bengbu233030,China)
With R&D input and output data of six Northern cities of Anhui province during 2010~2014 period as samples, The overall efficiency, technical efficiency, scale efficiency and returns to scale had be estimated by using DEA model;By establishing fixed effects variable intercept model containing period impact to test whether R&D funding intensity on the overall efficiency was significant or not. The study found: R&D input and output levels were lower in six Northern cities of Anhui province, The overall efficiency of R&D had significant spatial heterogeneity, The overall efficiency of research and development in Northern Areas of Anhui province showed an increasing trend in the 2010~2014 period, and R&D funding intensity had significant negative impact on the overall efficiency.
DEA model; R&D funding intensity; fixed effects model
2016-11-07
安徽省教育厅重点项目“皖北地区高新技术产业政府支持策略研究”(SK2016A0588);安徽省教育厅重点项目(SK2017A0628)。 作者简介:李少付(1969-),男,安徽蚌埠人,副教授,硕士,研究方向:应用统计与计量;张娜(1978-),女,安徽蚌埠人,副教授,硕士,研究方向:区域经济。
F127
A
1009-9735(2017)02-0032-06

