具反馈控制和时滞的离散竞争系统的持久性
余胜斌
(阳光学院 基础教研部,福建 福州 350015)
具反馈控制和时滞的离散竞争系统的持久性
余胜斌
(阳光学院 基础教研部,福建 福州 350015)
研究具有反馈控制和时滞影响的非自治离散竞争系统的持久性问题,通过运用差分不等式,得到了保证该系统永久持续生存的充分性条件。所得结果改进了现有的工作。数值模拟表明,本文结果具有可靠性。
持久性;离散;竞争;反馈控制;时滞
0 引言
对任一非负有界序列{f(n)},本文恒设:
众所周知,在一个生态系统中,两种群之间的关系有四种:捕食者与被捕食者,寄生物与寄生,两种群相互竞争,两种群互惠共存。近年来,诸多学者开始研究竞争系统的动力学行为[1-7],得到了丰富的结果。唐帆和刘志军[1]提出并讨论了如下具反馈控制和时滞的离散竞争系统:
(1)

(2)
通过应用概周期函数壳理论和构造Lyapunov函数的方法,文[1]得到了系统(1)正概周期解的存在性和全局吸引性的充分条件,给出了如下系统(1)的持久性的结论:

从条件(H0)可以看出,该系统的持久性与反馈控制变量有关。但是最近诸多具反馈控制的离散型生态系统的持久性研究结果均表明,反馈控制变量不会影响系统的持久性[8-10]。于是,我们就有了如下有趣的问题:反馈控制变量是否也不会影响系统(1)的持久性呢?事实上。通过采用文献[8-10]的分析手法,我们将得到如下结果:

注1:通过对比定理1和定理2可知,条件(H)比条件(H0)弱化了很多,故我们的结论实质性地改进了唐帆和刘志军[1]的结果。此外,定理2的条件(H)与反馈控制变量无关,说明系统(1)的持久性与反馈控制变量无关。
1 主要引理及证明
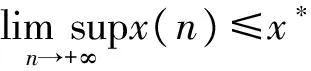
引理2[11]假设A>0,y(0)>0且y(n+1)≤Ay(n)+B(n),n=1,2,…,则有
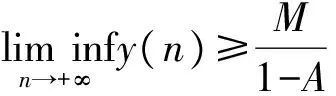
引理3[11]假设A>0,y(0)>0且y(n+1)≥Ay(n)+B(n),n=1,2,…,则有

引理4[1]设(x1(n),x2(n),u1(n),u2(n))T为系统(1)的任一正解,则有:
证明 由引理4可知,对∀ε>0,存在N1>0,当n≥N1时,有
由条件(H1),对上述的ε>0,我们可以找到足够小的β1>0,使得
(3)
由上式及系统(1)的第一个方程可知,当n≥N1+r时,
x1(n+1)
(4)
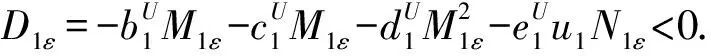
即
(5)
由系统(1)的第三个方程容易得到
(6)

(7)

(8)
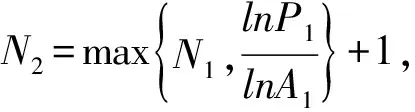
(9)
固定N2,则当n≥N1+N2时,有
(10)

由(3)式、(9)式、(10)式和系统(1)的第一个方程得,

(11)
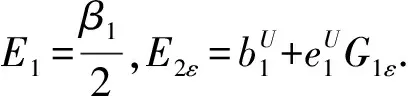




与引理5的证明类似,我们可以得到如下结论:
由引理5和引理6可知,定理2成立。
2 应用举例
本节通过举例验证结果的可行性。
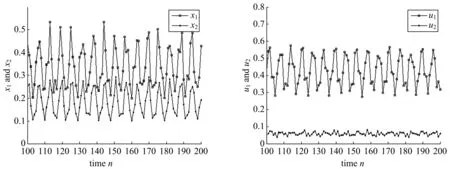
图1 具初始条件(0.2,0.4,0.1,0.2)T,(0.4,0.3,0.11,0.3)T,(0.1,0.6,0.4,0.7)T和(1.1,0.3,0.5,1.2)T的系统(12)的数值模拟结果
例1 考虑系统
(12)
对应于系统(1),由引理4可知,

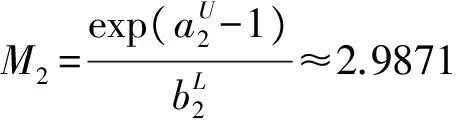
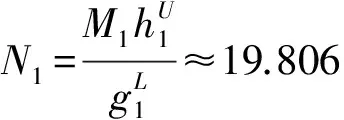
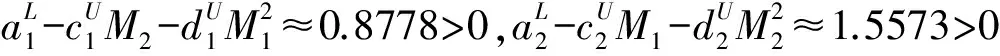

即定理1的条件(H0)不满足,所以根据定理1是没办法得到持久性的结论的,故本文结果极大地改进了文[1]的结果。
3 结论
本文研究了具有反馈控制和时滞影响的非自治离散竞争系统的持久性问题,通过运用差分不等式,得到了保证该系统永久持续生存的充分性条件。所得结果不但弱化了文献[1]关于持久性的条件,还表明该系统的持久性确实与反馈控制变量无关,从而极大了改进了文献[1]的工作。数值模拟表明了本文结果的可靠性。
[1]唐帆,刘志军.一类具有反馈控制的概周期时滞差分竞争系统(英文)[J].生物数学学报,2016,31(1):28-46.
[2]Yue Q. Extinction for a Discrete Competition System with the Effect of Toxic Substances [J].Advances in Difference Equations,2016 (1):1-1.
[3]余胜斌.一类离散非自治竞争系统的绝灭性和稳定性[J].延边大学学报(自然科学版),2015,41(4):279-284.
[4]余胜斌.具毒素影响的连续型竞争系统的绝灭性和稳定性[J].延边大学学报(自然科学版),2016,42(3):196-202.
[5]Chen F D,Xie X D,Miao Z S ,et al. Extinction in two Species Nonautonomous nonlinear Competitive System[J].Applied Mathematics and Computation,2016,274(1):119-124.
[6]Chen F D, Gong X J, Chen W L. Extinction in two Dimensional Discrete Lotka-Volterra Competitive System with the Effect of Toxic Substances(II)[J]. Dyn. Contin. Discrete Impuls. Syst., Ser. B, Appl. Algorithms, 2013(20): 449-461.
[7]Yu S B. Extinction for a Discrete Competition System with Feedback Controls [J].Advances in Difference Equations, 2017(1):9-9.
[8]Yu S B. Permanence for a Discrete Competitive System with Feedback Controls [J]. Communications in Mathematical Biology and Neuroscience, 2015: Article ID 16.
[9]余胜斌,张杰华.具时滞和反馈控制的修正Leslie-Gower离散系统的持久性[J].应用泛函分析学报,2014,16(3):244-249.
[10]ChenFD.PermanencefortheDiscreteMutualismModelwithTimeDelays[J].MathematicalandComputerModelling, 2008, 47(3-4): 431-435.
[11]WangLL,FanYH.PermanenceforaDiscreteNicholson’sBlowiesModelwithFeedbackControlandDelay[J].InternationalJournalofBiomathematics, 2008, 1(4): 433-442.
Permanence of a Discrete Competitive System with Delayand Feedback Controls
YU Shengbin
(DepartmentofBasicTeachingandResearch,YangoUniversity,Fuzhou350015,China)
A noautonomous discrete competitive system with time delay and feedback controls is studied in this paper. By using difference inequality theory, a set of conditions which guarantee the permanence of system is obtained. The results indicate that feedback control variables have no influence on the persistent property of the system. Our results not only supplement but also improve the existing work. The numerical simulations show that the results are reliable.
permanence; discrete; competitive; feedback controls; delay
2017-03-26
2016年福建省高校杰出青年科研人才培育计划;福建省自然科学基金资助项目(2015J01012、2015J01019)。
余胜斌(1984-),男,福建仙游人,硕士,讲师,研究方向:生物数学。
Q-332
A
1009-9735(2017)02-0038-04

