变增益PI控制器在开关磁阻电机中的应用
宋世潮,曲兵妮,宋建成
(太原理工大学,太原030024)
0 引 言
开关磁阻电机(以下简称SRM)具有结构简单、坚固,成本低,起动转矩大,起动电流小等特点,这使开关磁阻电机调速系统(以下简称SRD)非常适用于纺织、电动汽车和采矿等传动控制领域[1-4]。然而SRD是高度非线性系统,传统的固定参数PI控制器不能满足整个调速范围内的性能要求。非线性控制器虽然能够改善控制效果,但是控制器设计复杂,实现成本高,限制了SRM的工业应用。
针对SRD高度非线性的特点,国内外学者将非线性控制理论[5-6]引入到SRD中,取得了一定效果。同时,许多智能控制方法也被应用于SRD中,如模糊控制[7-8]、神经网络控制[9]等;文献[10]以小信号分析为基础,通过建立系统小信号动态模型,采用经典控制理论整定控制器PI参数,整定完成后控制器PI参数固定不变,只在一定调速范围内具有良好的动静态响应特性。文献[11]提出了一种积分型滑模变结构与神经网络补偿相结合的控制策略,使用积分补偿方法降低系统的振动与稳态误差,通过引入神经网络补偿控制环节,改善了系统的动静态性能。该方法采用的滑模变结构控制器与神经网络控制器,设计过程复杂,实现成本较高。文献[12]通过采用参数自适应的SRM转速电流双闭环控制策略,提高了SRD的稳定性和快速性,控制器根据转子位置自适应调节PI参数。
实践证明,要实现SRM在整个调速范围内良好的动态品质、控制相对简单的要求,需要在考虑SRD非线性的同时兼顾实现成本。SRD精确动态模型难以建立,而PI调节器的优点就在于即使受控对象的模型未知,其比例、积分常数亦可通过系统实际运行现场整定出来。SRD在不同的控制方式下,其参数和结构都是变化的,固定参数的PI调节器不能满足要求,必须引入参数自适应PI调节器。针对上述存在的问题,本文的目标是设计出变增益PI转速控制器,以实现PI参数随系统运行状态自适应调节,使SRM在整个调速范围内具有良好的动态性能。
1 SRM模型建立
SRM工作原理是基于磁通总是沿着磁阻最小的路径闭合。图1为本文研究的12/8极SRM定转子结构示意图。当转子位置处于图1的位置时,若给B相绕组通电,电机逆时针旋转;若给C相绕组通电,电机则顺时针旋转。
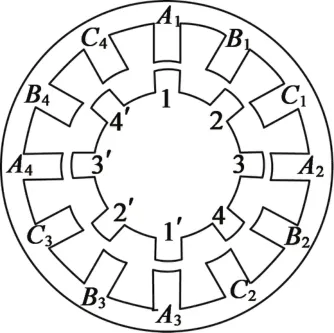
图1 12/8极SRM定转子结构图
SRM第k相绕组的电压方程:

式中:uk为第k相电压;ik为第k相电流;Rk为第k相电阻;Ψk为第k相磁链。
SRM第k相电磁转矩表达式:

式中:Tk为电机的第k相电磁转矩;W(ik,θ)为第k相绕组磁共能。
假定电机各相对称,忽略相间电感,相绕组的电感与电流大小无关,可得SRM简化线性模型[13]:
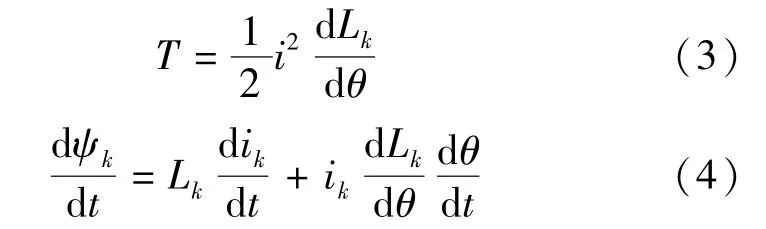
式中:Lk为第k相绕组电感。
简化线性模型下相电感对转子位置变化关系可表示[14]:
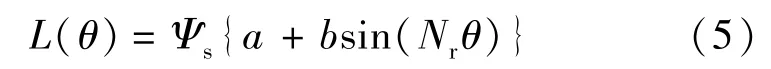
式中:Ψs为饱和磁链;Nr为转子极数。
电机电磁转矩T与负载扭矩TL作用下的转子机械运动方程式:
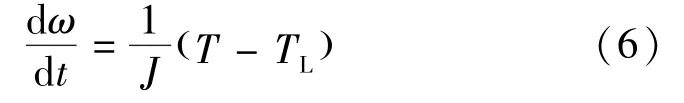
式中:ω为转子角速度;J为电机转子与负载的转动惯量。
建立了SRM简化模型,得出了相绕组电感L与转子位置角θ对应关系,忽略电流对相电感的影响,在此基础上设计变增益PI控制器。
2 控制器设计
以一相绕组为分析对象,由式(1)与式(4)可得:
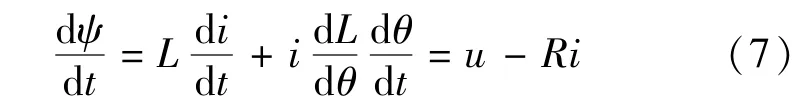
将式(3)与式(5)代入式(6)可得转速变化率:
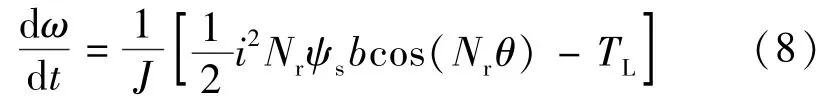
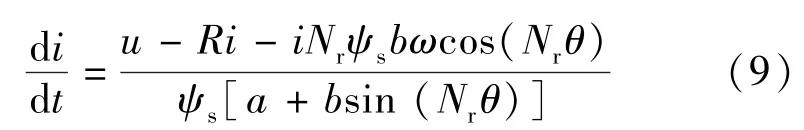
电阻压降远小于控制电压,因此可忽略电阻压降;由于SRM机械惯性大,电流动态响应速度相比机械状态变量要快得多,电流内环动态响应速度相比转速外环也要快得多[15]。SRM工作在单相励磁模式下,任意时刻只有一相绕组通电,励磁绕组通电后,电流迅速达到稳态,稳态后相绕组电流表达式:
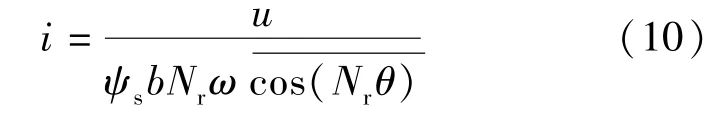
式中在相绕组通电励磁阶段的平均值。
将式(10)代入式(8)可得:
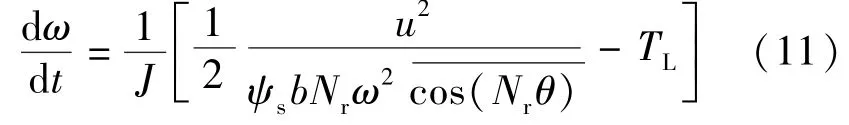
令f代表转速变化率,其在平均转速ω和平均控制电压两个工作点附近的小信号线性化方程:

式中
达到稳态后转速变化率的小信号线性化方程可表示:
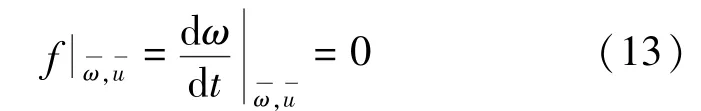
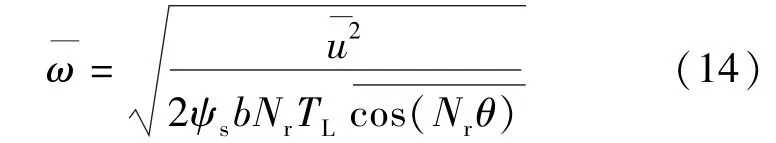
根据式(13)可得稳态平均转速可表示:根据式(14)与式(12)进一步推导可得:
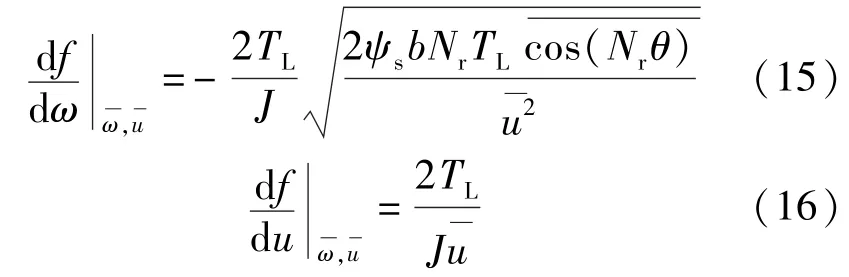
再将式(15)与式(16)代入式(12)可得线性化方程表达式:
用Trizol提取总RNA,采用PrimeScript® RT reagent Kit进行逆转录,采用miRNA特异性引物扩增miR-219。采用SYBR试剂在IQ5光学系统实时PCR机上进行qRT-PCR。β-actin和U6分别作为mRNA和miRNA的内参。采用2-ΔΔCt法定量计算,试验重复3次。
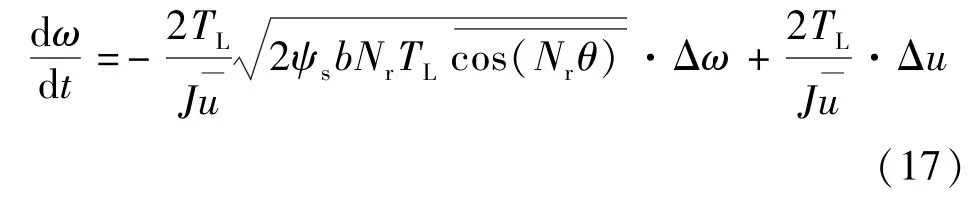
对式(17)等式两边进行拉普拉斯变换,可得转子角速度小信号Δω(s)与控制电压小信号Δu(s)之比:

式中
式(18)为电机s域一阶模型传递函数。
PI控制器是SRM调速系统的必要环节,其传递函数:
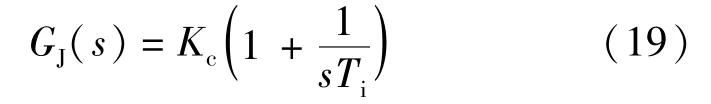
式中:Kc为比例系数;Ti为积分时间常数。
不同于传统PI控制器,变增益PI控制器比例增益Kc与积分时间常数Ti需要随系统运行状态的变化自适应调节。式(18)为SRM一阶动态模型,是一阶惯性环节,PI控制器比例增益Kc、积分时间常数Ti应与系统参数Kp,Tp成函数关系。结合SRM一阶动态模型与PI控制器传递函数,变增益PI控制器比例增益Kc、积分时间常数Ti与系统参数表达式可取:
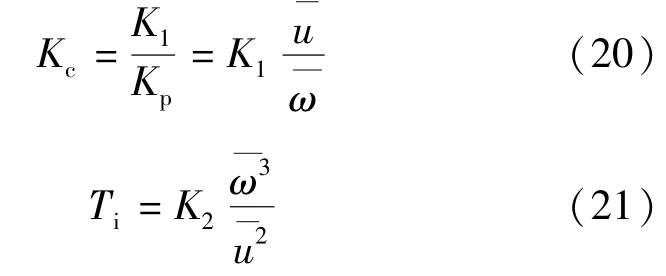
式中:K1为比例修正系数;K2为积分修正系数。
针对具体的SRM及其应用场合,K1与K2需要经过实验调节获取。
3 实验分析
3.1 实验方案
本文将一台三相12/8极SRM作为实验样机,其额定数据如下:额定功率7.5 kW,额定电压直流514 V,额定转速1 500 r/min,最高转速2 000 r/min。控制核心采用DSP,型号为TMS320LF2407A,主电路采用三相不对称半桥式结构。
电机电感和磁链数据通过有限元分析得到,饱和磁链Ψs=1.59 Wb,转子位置角为0°时电感Lu=12.11 mH,转子位置角为25°时电感La=39.03 mH,转子极数Nr为8极。根据式(5)可得,a=0.076,b=0.147。
本文基于DSP的SRD控制原理图如图2所示。SRD系统主要由SRM、控制器、功率变换器、位置传感器4部分组成。虚线框内部为控制器部分,采用软件编程实现内部功能。
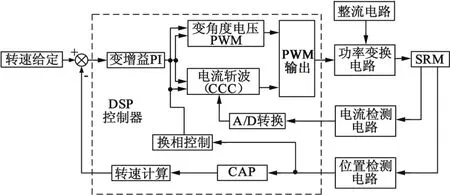
图2 SRD控制系统框图
变增益PI控制器的输入为给定转速与实际转速的差值,输出根据电机转速的高低分别作为参考电流或占空比。系统工作在电流斩波与变角度电压PWM两种控制方式下,实际转速的高低决定所要采用的控制方式,实际转速和控制电压共同决定PI参数。通过对转速差进行自适应PI调节后,控制SRM的转速,实现系统在整个调速范围内稳定运行。
3.2 实验结果
工业应用场合要求调速系统在不同运行状态下都具有良好的动态性能。本文在传统PI及变增益PI两种控制模式下,分别测试了系统于100~1 500 r/min转速区间内的动态性能。测试实验在SRD系统和加载操作台上完成,动态响应曲线由加载操作台采集的数据绘制而成。系统实验平台如图3所示所示。

图3 SRD系统实验平台
系统在传统PI和变增益PI两种控制方式下,给定转速为500 r/min、运行电压为额定514 V时的三相绕组电流波形分别如图4(a)和图4(b)所示。
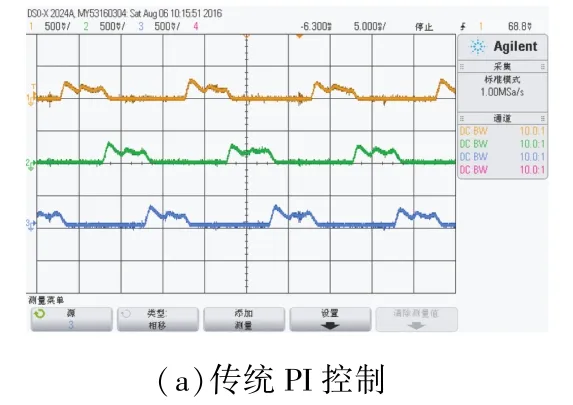
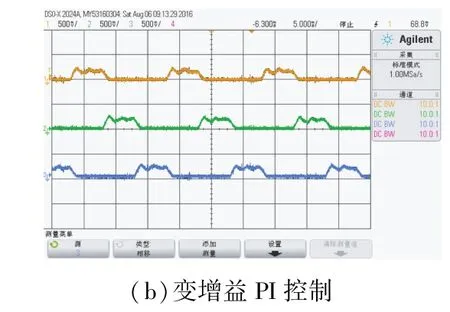
图4 相绕组电流波形(截图)
图4中,系统工作在电流斩波控制方式下。采用传统PI控制方式时,三相电流波形对称,绕组电流基本控制在斩波上下限范围之内,但在每相绕组电流上升区有斩不住的趋势;采用变增益PI控制方式时,三相电流波形对称,绕组电流能够良好地控制在斩波上下限范围之内,基本为平顶波。
图5是SRD在传统PI和变增益PI两种控制方式下的动态性能对比结果。传统PI控制器比例系数Kc整定为0.37,积分时间常数Ti整定为1.2;变增益PI控制器比例系数Kc整定为0.93u/ω,积分时间常数Ti整定为3.84×10-4ω3/u2。电机在两种控制方式下的转速响应曲线分别如图5所示。曲线1为变增益PI控制下的响应曲线,曲线2为传统PI控制下的响应曲线。
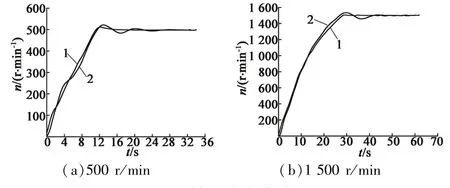
图5 转速响应曲线
图5(a)中,给定转速为500 r/min,电机在传统PI控制方式下,转速超调为4.5%,经过两个振荡周期14 s后达到稳态;在变增益PI控制方式下,满足快速响应的同时,转速超调为1%,且能够迅速达到稳态。图5(b)中,给定转速为1 500 r/min,电机在传统PI控制方式下,由于PI参数固定不变,转速超调为3.5%,振荡周期也变长;在变增益PI控制方式下,PI参数能够根据实际转速自适应调节,超调明显减小为0.5%,且快速达到稳态。可以得出:采用变增益PI控制方式时,系统转速动态响应性能更优,解决了传统PI控制快速响应时超调大的矛盾。
给定转速为额定转速1 500 r/min时,系统稳定运行后,突加和突减负载时,电机在传统PI控制方式和变增益PI控制方式下的动态响应曲线如图6所示。曲线1为变增益PI控制下的响应曲线,曲线2为传统PI控制下的响应曲线。
图6中,电机在传统PI控制方式下,突加10 N负载后,速度降落为200 r/min,经过30 s恢复到稳态;所加负载扰动消失后,速度突升160 r/min,经过20 s恢复到稳态。

图6 动态响应曲线
电机在变增益PI控制方式下,速度降落为30 r/min,经过6 s恢复到稳态;所加负载扰动消失后,速度突升30 r/min,经过7 s恢复到稳态。可以得出:采用变增益PI控制方式时,SRD根据实际转速自适应调节PI参数,具有更好的抗扰性能。
4 结 语
本文以7.5 kW SRM为研究对象,设计了变增益PI控制器,得出研究结论如下:
1)理论分析SRM数学模型与电感特性,建立了电机转速环s域一阶动态模型,给出了PI参数随控制电压和转速变化表达式,设计了工程实现简单、参数自适应的变增益PI转速控制器。
2)利用SRD实验平台对比了传统PI和变增益PI两种控制器的控制效果。实验结果表明:变增益PI控制器能够根据电机转速变化自适应调节PI参数,在宽广的调速范围内实现了动态响应快,超调小,抗扰动性能好的控制目标,从而对SRM在工业传动系统的广泛应用具有参考价值。
参考文献
[1] WANG S,ZHAN Q,MA Z,et al.Implementation of a 50-kW fourphase switched reluctance motor drive system for hybrid electric vehicle[J].IEEE Transactions on Magnetics,2005,41(1):501-504.
[2] SCHULZ S E,RAHMAN K M.High performance digital PI current regulator for EV switched reluctance motor drives[C]//37th IAS Annual Meeting.Conference Record of the IEEE,2002(3):1617-1624.
[3] HA K,LEE C,KIM J,et al.Design and development of low-cost and high-efficiency variable-speed drive system with switched reluctance motor[J].IEEE Transactions on Industry Applications,2007,43(3):703-713.
[4] KIYOTA K,KAKISHIMA T,CHIBA A,et al.Cylindrical rotor design for acoustic noise and windage loss reduction in switched reluctance motor for HEV applications[J].IEEE Transactions on Industry Applications,2016,52(1):154-162.
[5] 修杰,夏长亮.基于遗传算法的开关磁阻电机自适应模糊控制[J].电工技术学报,2007,22(11):69-73.
[6] HANNOUN H,HILAIRET M,MARCHAND C.High performance current control of a switched reluctance machine based on a gainscheduling PI controller[J].Control Engineering Practice,2011,19(11):1377-1386.
[7] 张艳杰,徐丙垠,熊立新,等.一种基于SRD模糊控制的风力机模拟器[J].电机与控制学报,2011,15(1):38-43.
[8] RODRIGUES M,COSTA BRANCO P J,SUEMITSU W.Fuzzylogic torque ripple reduction by turn-off angle compensation for switched reluctance motors[J].IEEE Transactions on Industrial Electronics,2001,48(3):711-715.
[9] LIN Z,REAY D S,WILLIAMS B W,et al.Online modeling for switched reluctance motors using B-spline neural networks[J].IEEE Transactions on Industrial Electronics,2007,54(6):3317-3322.
[10] 王宏华,许大中,陈永校.开关型磁阻电动机脉宽调压调速系统小信号模型及调节器设计[J].电工技术学报,1997(3):1-5.
[11] 李永坚,许志伟,彭晓.SRM积分滑模变结构与神经网络补偿控制[J].电机与控制学报,2011,15(1):33-37.
[12] 王喜莲,许振亮.基于PI参数自适应的开关磁阻电机调速控制研究[J].中国电机工程学报,2015,35(16):4215-4223.
[13] MILLER T J E.Brushless permanent-magnet motor drives[J].Power Engineering,1988,2(1):55-60.
[14] 王宏华.开关磁阻电机调速控制技术[M].北京:机械工业出版社,1995
[15] HO W K,PANDA S K,LIM K W,et al.Gain-scheduling control of the switched reluctance motor[J].Control Engineering Practice,1998,6(2):181-189.

