永磁同步电动机神经元PID控制设计与仿真
于 淼,娄 鹏,孙 伟
(中国电子科技集团公司第二十一研究所,上海200233)
0 引 言
对于永磁同步电动机而言,矢量控制技术的出现使得交流电动机的控制性能得到了质的提升[1],矢量控制的核心是励磁电流和转矩电流的解耦控制,并解决了交流电机自身耦合的不足。直接转矩控制技术也是基于磁场与转矩分别独立控制的思想,但采用的是比较巧妙的技术——具有继电器特性的砰砰控制和电压矢量查询表[2]。
永磁同步电动机控制不仅要调节的变量多,且模型还有复杂的非线性、强耦合等特点,工作情况复杂,诸多电动机参数都会发生着一定程度的变化,从而影响着交流电动机的实际控制性能[3]。随着自动控制技术的飞速发展,一些先进的控制方法不断涌现,参数辨识技术、自适应控制技术、基于神经网络和模糊控制等先进的控制控制算法逐步融入到电动机控制技术中,一定程度提高电机控制的快速稳定性和鲁棒性[4]。
1 永磁同步电动机转子磁场定向矢量控制
为了建立一个可以从0°到360°可控的磁场,需要利用α-β坐标系和d-q坐标系,以方便系统模型变量解析,iABC-iαβ变换与iαβ-idq变换如图 1 所示[5]。

图 1 iABC-iαβ变换与变换
电磁转矩Te对能够使定子和转子产生相对运动,永磁同步电动机的调速控制,即是控制电机内部的电磁转矩Te[6]。永磁同步电动机在dq转子坐标系中的转矩公式:
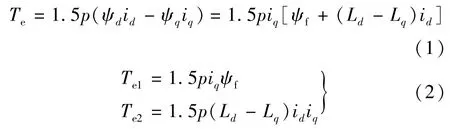
可见转矩分量都与iq成正比,因此若要控制永磁同步电动机磁场转矩,实现转矩伺服或者速度伺服,可以通过调节定子电流转矩分量来实现。
2 神经元解耦控制
神经元解耦算法具有在线学习整定系统参数、消除耦合的优势,成熟的神经元解耦器不断运用在控制系统中[7]。单神经元网络可以由一个或者多个神经元组成,X定义输入模式的元素,T定义目标相关联的元素,利用单输入神经元样本,求取最小偏差值y,可以用来实现系统的解耦控制问题,其对应的解耦过程如图2所示。
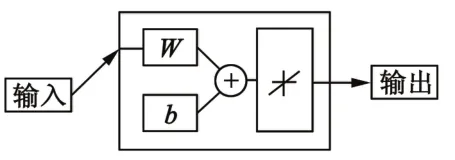
图2 解耦过程图
图2对应的解耦过程可以理解为如下的数学公式:
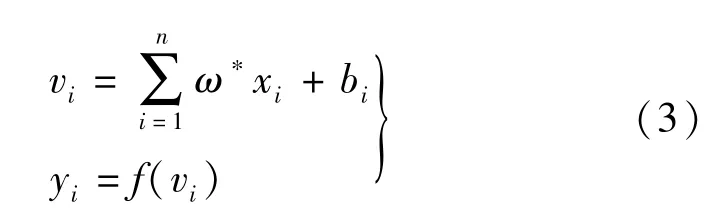
其向量形式可以表示成:

式中:xi为给定输入信号变量;bi为神经元i的阈值;ω是神经元i连接权值;f(·)称为激发函数或响应函数。MATLAB中算法实现如图3所示。
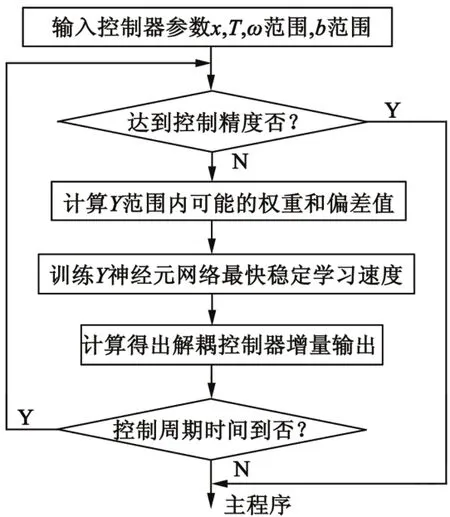
图3 算法流程图
永磁同步电动机的控制模型对应输入输出可以表示:
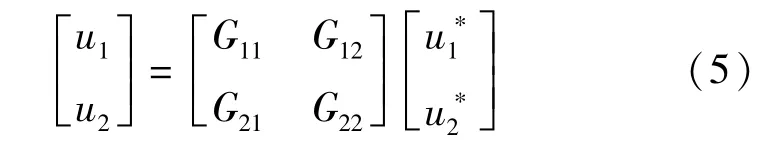
将单神经元解耦控制器融入到永磁同步电动机控制模型后,式(5)便可以得到一个广义对象,可以表示:
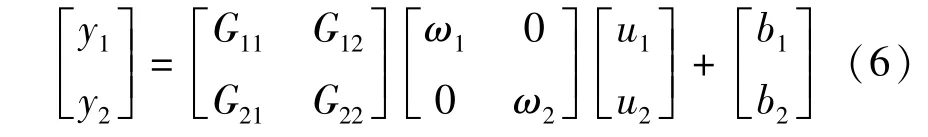
采用W-H学习规则修订正权矢量,即采用最小均方和作为网络收敛的准则。神经网络的目标训练公式:
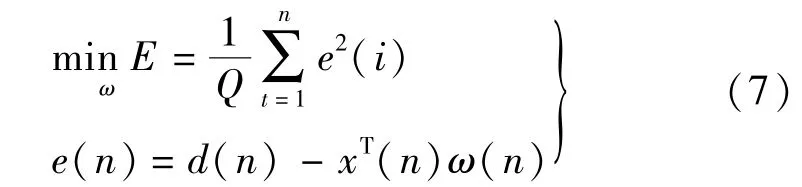
Q是给定模型的取样数目,神经网络调整的过程是找到最优的权值ω,使得模型误差结果均方差达到最小。通过用对权值ω求偏导,令该偏导的表达式等于零,即可求解得出的极值。
建立永磁同步电动机单神经元解耦控制系统模型如图4所示。电机控制系统动态结构图中包含两个闭环控制,一个是转速的外环控制,另一个是电流的内环控制。电流调节器和转速调节器模型的输入端均加上PI模块和神经元解耦模块,目的在于消除控制模型的系统误差和变量解耦。
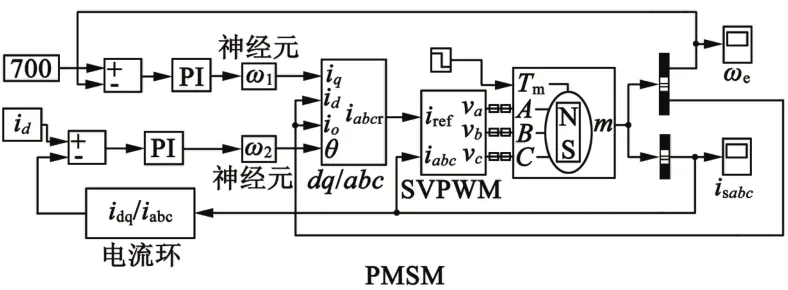
图4 模型结构图
在MATLAB仿真模块中建立单神经元永磁同步电动机控制系统模型,神经元解耦控制器外部接入多个延迟节拍,映射相应的控制算法。针对神经元解耦算法研究,图4中永磁同步电动机本体模型使用仿真模型库中现有的模型,这种理想的线性模型对应的输入输出也存在耦合情况。
权值ω是一个在线学习且不断整定的值,在系统启动后开始自学习,最终收敛,如图5所示。系统误差收敛且趋于0后,ω收敛于定值。
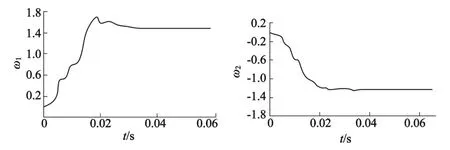
图5 单神经元解耦控制器ω调整过程
输入速度指令并使电机运转在此转速下,瞬间施加25 N·m转矩,此时电机对应的转速波动波形如图6所示。

图6 突加力矩载荷响应曲线比对比
单神经元解耦控制模型转速响应明显比常规PID控制快,且转速上下跳变值低。瞬间施加转矩前,这两类不同策略模型对应的转速波动为4 r/min。瞬间施加转矩后,采用神经元的控制模型电机转速未出现明显振荡,受到突加转矩的影响,转速略微掉至996 r/min,然后在2 r/min内波动,最后稳定到996 r/min。采用常规PID的控制模型在突加载荷瞬间转速掉至975 r/min,突变较大,在转速996 r/min稳定之前出现了明显的波动。
3 PID控制器设计
PID中加大kp值能提高系统调整速率,同时可能会使控制系统振荡现象加剧,调整ki值的目的在于削弱系统稳态误差,但使模型过渡时间增加,添加kd值能够避免调节对象溢出,却会使系统在一定程度上响应速度降低。因此传统的PID控制方法对于转矩和转速控制精度要求高的永磁同步电动机伺服控制系统难以满足。在控制系统中发挥神经网络的在线学习优势,根据阶跃区间信号和系统所能承受的“能力”来调整优化PID参数值。本文根据电机系统控制特性设计一种PID控制器,在不同的控制区间整定出最优的控制参数,快且无超调,使控制器的适应性大大改善。
一般的控制系统都具有如图7所示的响应波形。按特征阶段分为4个区间,可以根据图7中的波形整定PID调节器在不同的阶跃区间系数。
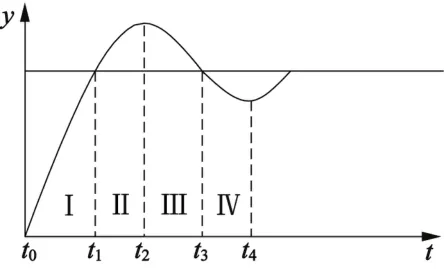
图7 控制系统分区间阶跃响应波形
(1)比例增益系数kp
Ⅰ区间,控制系统作用初始阶段,响应速度要求快,应增加kp值,但kp过大会引起系统出现超调,因此在控制系统接近输入值时适当减小kp值。Ⅱ区间,为了加快向下调节作用,使控制系统调整速度加快,kp值应缓慢增加。Ⅲ区间,降低控制系统输出滞后,使控制量平稳,kp应该缓慢降低;Ⅳ区间,kp应缓慢加大,效果与Ⅱ区间类似。另外kp主要是加快响应速度,获得较小的超调量,因此可以设计kp值与e(t)绝对值成正比。根据上述整定趋势,把kp与系统偏差e(t)的对应关系描述为如下函数模型:
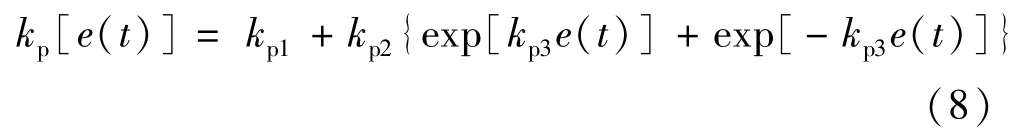
(2)积分增益系数ki
在控制系统误差变大阶段,减小ki值可以降低系统超调效果,避免控制系统出现振荡响应结果;在控制系统误差变小后,增大ki值可以削弱稳态误差。因此,把ki与系统偏差e(t)的对应关系描述为如下函数模型:

式中:ki2调整ki的变化速率。
(3)微分增益系数kd
Ⅰ区间,控制系统作用初始阶段,给定一个较小的kd值,并使其缓慢增加,可以避免出现超调,同时不会干扰控制系统响应灵敏度;Ⅱ~Ⅳ区间,进一步加大kd可以增强系统的向下能力,降低超调幅值。但随着响应延长,kd值应该锁定在一段区间内。
ev(t)为偏差e(t)的变化速率,其符号需要被考虑,把kd与系统偏差e(t)和ev(t)的对应关系描述为如下函数模型:
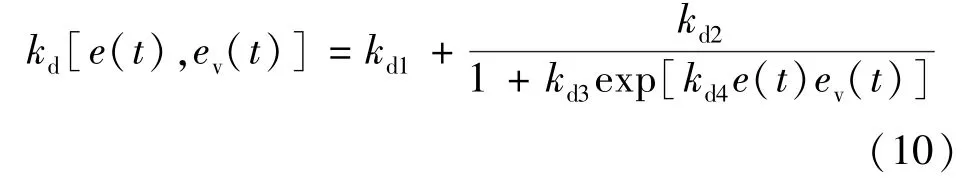
式中:kd4调整kd的变化速率。
4 仿真结果
在控制模型中给定电机载荷为30 N·m转矩,分别使用常规的PID控制模型和本文设计的单神经元解耦PID模型,电机起动从零转速增加至1 000 r/min,对应的速度曲线如图8所示。
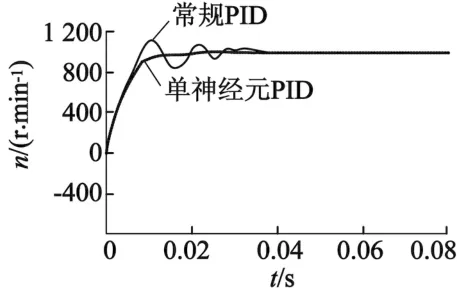
图8 转速波形对比
在控制模型中卸掉负载,重新起动电机,在速度稳定在998 r/min情况下,瞬间施加30 N·m负载,对应的速度响应曲线如图9所示。
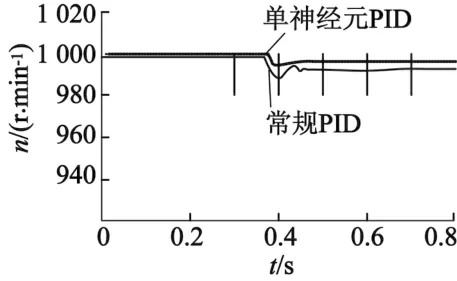
图9 神经元解耦与常规PID控制方式扰动响应曲线
分析仿真结果可知,本文的神经元PID控制虽然在一定程度上削弱了电机控制系统的响应速度,但是使控制系统没有超调,且增强了电机转速的稳定精度。对比常规的PID控制策略,电机转速稳态误差为2 r/min,转速超调量降低为3%,但系统的稳态误差接近0,被控量没有超出期望值,且调节过程中没有来回波动。瞬间施加转矩负载30 N·m时,转速最大偏差为6 r/min,对比分析可得本文的神经元PID使电机控制系统的抗干扰能力增加。
5 结 语
通过分析永磁同步电动机控制模型的被控对象与调节量,结合磁场定向矢量控制坐标变换数学原理,在MATLAB中建立永磁同步电动机仿真控制模型。在控制模型的速度环和电流环加入单神经元解耦器,以消除系统控制量与被控量相互耦合作用,根据控制系统分区间阶跃响应波形,设计一种PID控制器。通过仿真结果对比发现,神经元PID控制方法系统响应速度依然较快,且对比常规PID控制方式,超调和振荡效果被消除,且突加载荷,速度波动更小,验证了这种模型的正确性和可行性。
参考文献
[1] 秦忆.现代交流伺服系统[M].武汉:华中理工出版社,1995:37-42.
[2] 黄守道.电机瞬态过程分析的MATLAB建模与仿真[M].1版.北京:电子工业出版社.2013.
[3] 袁登科.永磁同步电动机变频调速系统及其控制[M].北京:机械工业出版社,2015.
[4] 徐邦荃.直流调速系统与交流调速系统[M].武汉:华中理工大学出版社,2000:156-287.
[5] 吴利刚.基于模糊逻辑的永磁同步电机控制算法研究[D].长沙:湖南大学,2012.
[6] 覃甫军.永磁同步电机伺服控制系统设计与仿真验证[D].成都:电子科技大学,2012.
[7] 孙冠群,于少娟.控制电机与特种电机及其控制系统[M].北京:北京大学出版社,2011:147-151.

