基于模糊PID的单连杆旋转机器人鲁棒控制
卢勇威,黄良永
(1.广西职业技术学院,南宁530227;2.广西科技师范学院,来宾546199;3.武汉理工大学,武汉410082)
0 引 言
无刷直流电动机[1](以下简称BLDCM)具有调速性能好、效率和可靠性高等优点,被广泛应用在机器人领域。为了实现机器人的精确控制,电机驱动系统的性能尤为重要。在机器人的控制中通常采用闭环控制系统,其中,比例-积分-微分(以下简称PID)[2]控制技术最为常见。
本文以BLDCM驱动的单连杆机器人为研究目标,单连杆机器人只包含一个可平面360°转动的机械臂。由于单连杆机器人在运动过程中受到的重力、向心力不同,致使其动力学模型具有非线性[3]。因此,传统PID控制器不能满足其非线性要求。机器人与人类不同,缺乏使用不准确信息解决问题的能力。为此,学者在 PID控制中融入了模糊理论[4],模糊控制器不需要了解系统的精确模型,使用语言规则来解决系统非线性问题[5]。因此,在存在参数变化和负载扰动下,模糊PID控制器仍然能够较好地工作。
基于上述分析,采用了一种新型的参数自整定模糊PID控制器,将模糊推理和PID控制相结合,并融入了参数自整定技术,以此动态调整PID参数,从而精确控制单连杆旋转机器人的位置。通过Simulink仿真和实际实验,证明了控制系统具有较高的控制精度,并对机械臂重力具有较好的鲁棒性。
1 单连杆旋转机器人模型
单连杆旋转机器人可以根据安装方式的不同,在垂直面或水平面转动。在水平面转动过程中,由于作用在机械臂中心的重力是一个常数,所以有效负载没有改变[6]。然而,在垂直面转动过程中,有效负载与它的运动方向有关。图1显示了机械臂在垂直面的360°范围内旋转时,由于重力引起的负载转矩的变化曲线。
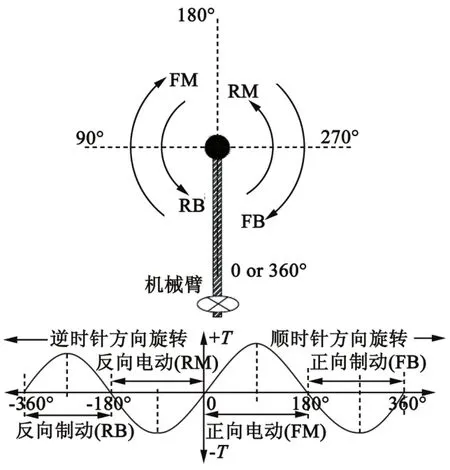
图1 单连杆机械臂在垂直面旋转时的转矩曲线
当机械臂以顺时针方向旋转时,重力会施加一个向下的力。为此,电机前半圈需要执行驱动,后半圈执行制动。其中电机驱动转矩在90°处最大,制动转矩在270°处最大。同理可知,当机械臂以逆时针方向旋转时也会出现同样的场景。然而,由于机械臂运动需要保持稳定,速度不能受负载转矩变化的影响,以此来确保机械臂能够准确到达目的位置。
电机的负载转矩曲线在两个方向上都类似于正弦波。因此,电机转矩Tm可定义如下:
Tm=TLsinθ(1)
式中:TL为机械臂重力引起的最大有效负载转矩;θ为机械臂的角度位置。
2 单连杆机器人控制系统
2.1 控制系统框架
由于机械臂在垂直面旋转时,负载转矩在不断变化,所以需要一种鲁棒性好的控制系统。本文的位置控制系统框架如图2所示。
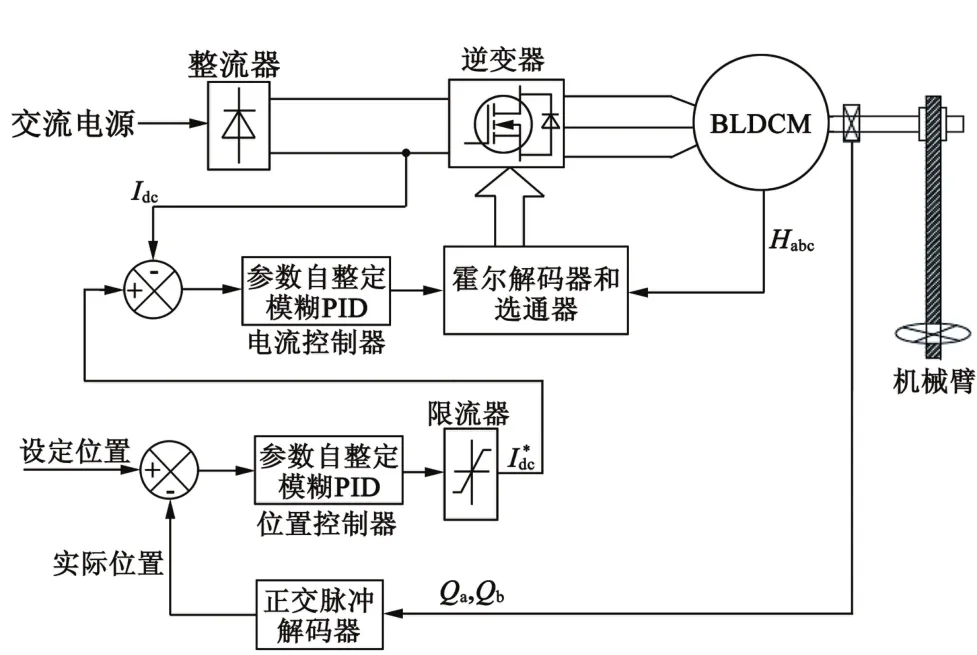
图2 机械臂位置控制系统框图
机械臂直接与电机传动轴相连接,并通过正交编码器[7]来获取机械臂的实际位置。通过比较机械臂的实际位置和设定位置获得位置误差,并反馈到位置控制器中。本文中,位置控制器采用了参数自整定模糊PID控制模型,输出为参考直流电流值。接着,将电流绝对值与实际测量的电流值Idc进行比较,得到电流误差反馈到电流控制器中。同样,电流控制器采用了参数自整定模糊PID控制模型。电流控制器的输出决定了电机驱动器的选通脉冲信号占空比。电机驱动器根据霍尔信号和电流控制器的输出来产生PWM信号,用来控制电机逆变器选通,从而控制电机转动。
2.2 参数自整定模糊PID控制器设计
在机械臂位置控制系统中,位置控制器和电流控制器是系统的核心,直接影响控制精度。这些闭环控制系统通常使用PID控制器,传统PID结构简单且容易操作,但是其性能较差,容易受到负载扰动和命令改变的影响。此外,控制增益的设计涉及复杂的数学建模。为此,本文采用了模糊PID控制器[8-9],它不需要复杂的数学建模,并且对工作环境的变化具有较好的鲁棒性。
参数自整定模糊PID控制器是利用模糊推理系统,根据系统实时控制误差参数来自适应地调节PID参数,使控制器能够根据环境变化达到最优设置。参数自整定模糊PID控制器的基本结构如图3所示。
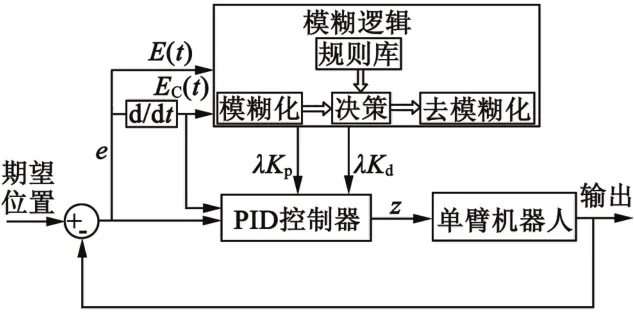
图3 参数自整定模糊PID的基本结构
将测量误差E和误差变化量EC作为PID控制器的输入,可以用来防止由于直接触发微分过程而产生参考信号的阶跃变化[10]。同时,将这两个参数也作为模糊推理系统的输入。模糊推理系统中使用的隶属度函数的范围为±1,因此,在模糊推理之前和之后需要对信号进行归一化和去归一化操纵。另外,位置控制器的输出为参考电流幅值±I*dc,电流控制器的输出为选通脉冲占空比(0~1)。
模糊推理系统分为4个步骤:1)模糊化;2)基于If-Then规则的知识库;3)模糊推理;4)去模糊化。模糊推理系统根据E和EC参数,通过模糊规则决策出最佳PID控制器参数Kp和Kd。
在本文中,输入和输出变量是通过隶属度值为0.5的三角隶属度函数进行映射[11]。其中,具有7个语言变量,即负大(NL),负中(NM),负小(NS),零(ZO),正小(PS),正中(PM)和正大(PL)。另外,推理机中采用Mamdani型推理机制[12],去模糊化过程采用重心法。图4分别显示了输入和输出的隶属度函数。
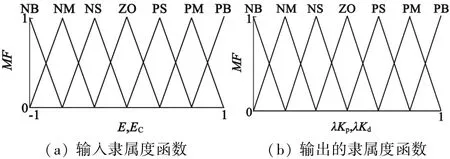
图4 隶属度函数
推理机基于7×7=49个模糊规则进行推理,模糊规则矩阵如表1所示。其中,矩阵的最顶行和最左列分别表示变量“E”和“EC”的模糊集,矩阵的主体为变量“u”。
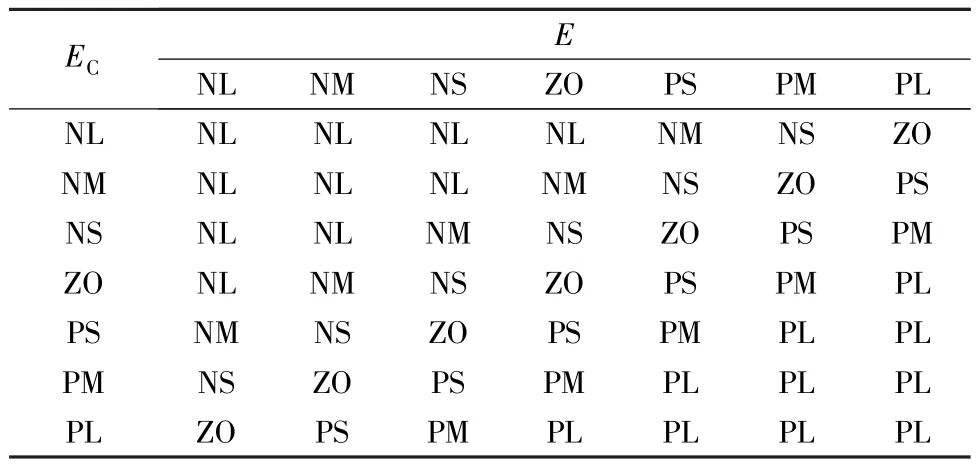
表1 模糊规则矩阵
推理过程分为两个阶段:1)根据输入的E和EC参数,对所有规则进行查询比较以确定适用于当前场景的规则;2)根据选择的规则作出控制决策。
这里使用“AND”操作对各规则的决策进行融合,以此作出最终决策,表达式如下:
μ(z)=min{μ(x),μ(y)} (2)
接着,对模糊推理得到的控制决策μ(z)进行去模糊化操作,即将模糊决策转换为实际值输出。其中,本文采用重心法来去模糊化。λ(E,EC)权重系数的表达式如下:
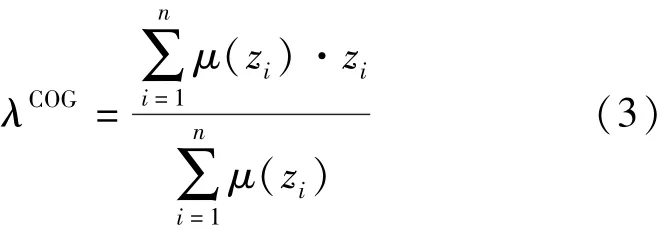
最后,PID控制器的自整定参数计算如下:
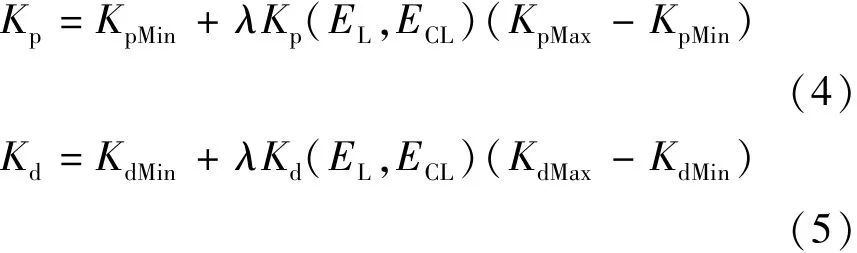
式中:λ为权重系数;KpMax,KpMin,KdMax,KdMin分别为比例增益和差分增益的最大和最小限制值。
3 仿真及分析
3.1 仿真设置
通过MATLAB/Simulink构建单连杆机器人位置控制器的仿真模型,其中,电机模型参数根据魔力公司的TETRA系列BLDCM设定,如表2所示。
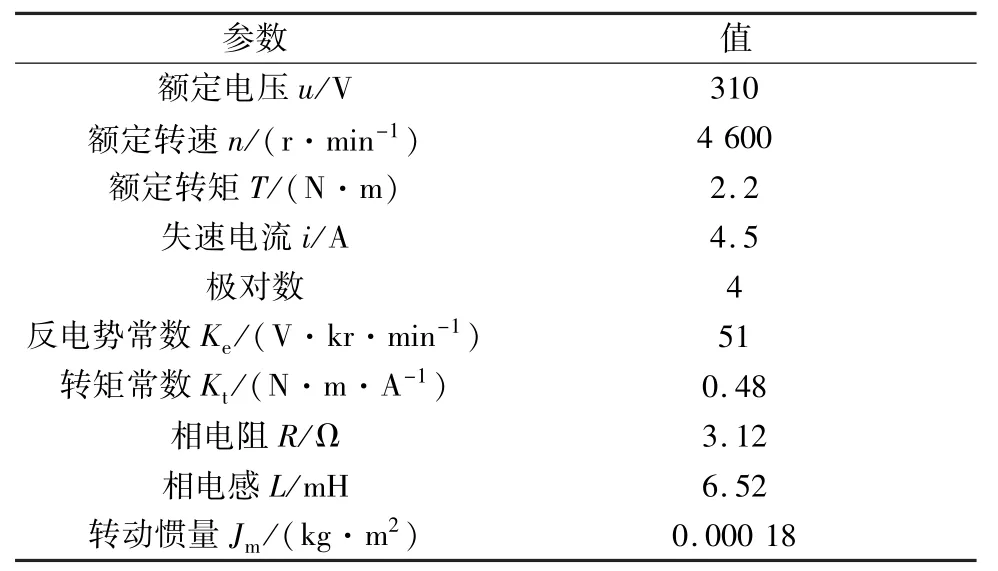
表2 电机参数
3.2 仿真结果
为了验证模糊PID控制系统的可行性,并将其与传统PID控制器的性能进行比较。根据机械臂的运动方向,执行4个仿真实验,即顺时针从0°转动到180°;顺时针从 180°转动到 360°;逆时针从 360°转动到180°;逆时针从180°转动到0°。同时对电机施加一个最大1 N·m的正弦型负载转矩来模拟机械臂受重力的影响(见图1)。
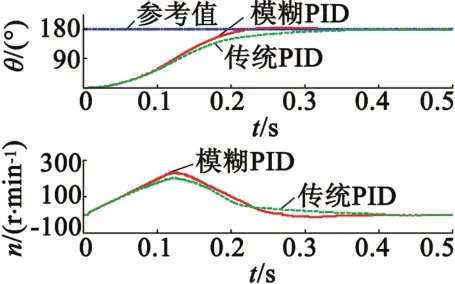
图5 正向电动模式(0°~180°)动态曲线
图5 给出了实验1中机械臂位置和电机转速的动态曲线。当机械臂从0°~180°顺时针转动时,驱动器执行正向电动模型,重力转矩为正,且在90°处最大。可以看出,传统PID控制机械臂转动到指定位置需要0.35 s的建立时间,而模糊PID只需要0.25 s。
图6给出了实验2中机械臂位置和电机转速的动态曲线。在机械臂从180°~360°顺时针方向向下转动时,驱动器执行正向制动模式,重力转矩为负。可以看出,传统PID的建立时间为0.2 s,比在正向电动模式中快。这是由于受到重力的影响,使机械臂向下转动速度变快,说明其对重力的鲁棒性较差。而模糊PID的建立时间为0.25 s,等于正向电动模式中的时间,具有较好的控制稳定性。另外可以看出,传统PID的过冲现象比较严重,而模糊PID则很小。
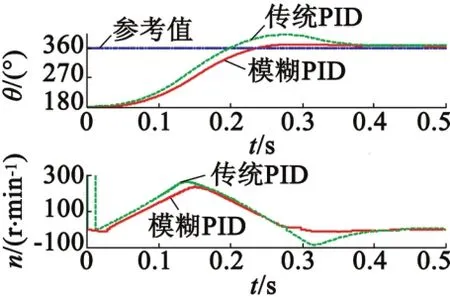
图6 正向制动模式(180°~360°)动态曲线
同样,图7和图8分别给出了实验3和实验4中,机械臂沿逆时针(360°~0°)转动时,机械臂位置和电机转速的动态曲线。其结果与顺时针转动实验类似,进一步证明了模糊PID控制器性能优越。
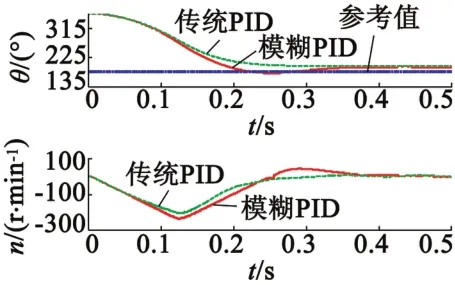
图7 反向电动模式(360°~180°)动态曲线
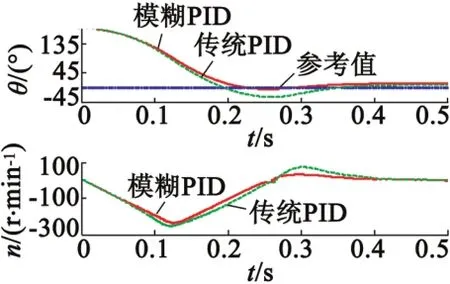
图8 反向制动模式(180°~0°)动态曲线
为了更加直观地比较传统PID和模糊PID的性能,表3列出了建立时间、最大过冲百分比和稳态误差百分比的比较结果。可以看出,模糊PID控制器要比传统PID控制器性能更优越。
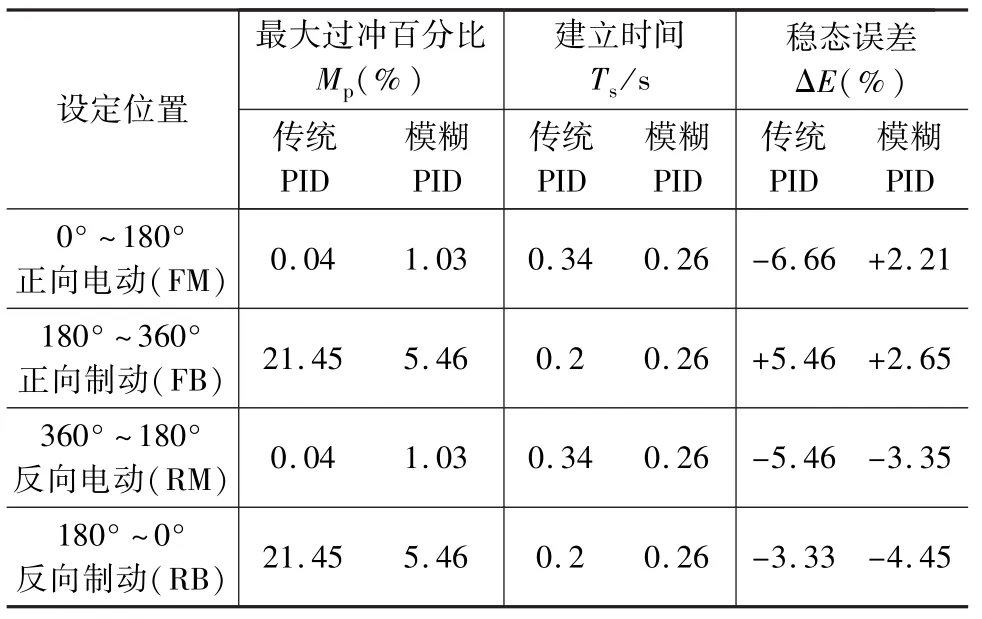
表3 仿真结果比较
4 实验及分析
构建了实际实验平台,通过DSP编程实现模糊PID控制器,单杆机械臂与电机轴传动机构连接,机械臂长度约为35cm,质量约为2 kg,经过传动机构后,由重力产生的电机负载扭矩最大约为1 N·m。电机参数如仿真分析中的表2所示。另外,利用三相智能功率模块来驱动电机。
图9分别给出了机械臂沿顺时针方向从0°转动到180°时,在具备传统PID和模糊PID的控制器中,机械臂位置曲线和电机转速曲线。可以观察到,传统PID控制器的位置建立时间约为0.37 s,而模糊PID需要约0.26 s,实验结果和仿真结果相似。说明了模糊PID控制器能够快速且稳定地控制机械臂转动到设定位置。

图9 正向电动模式(0°~180°)的响应
图10 分别给出了机械臂沿顺时针方向从180°转动到360°时,传统PID和模糊PID控制器的机械臂位置和电机转速曲线。
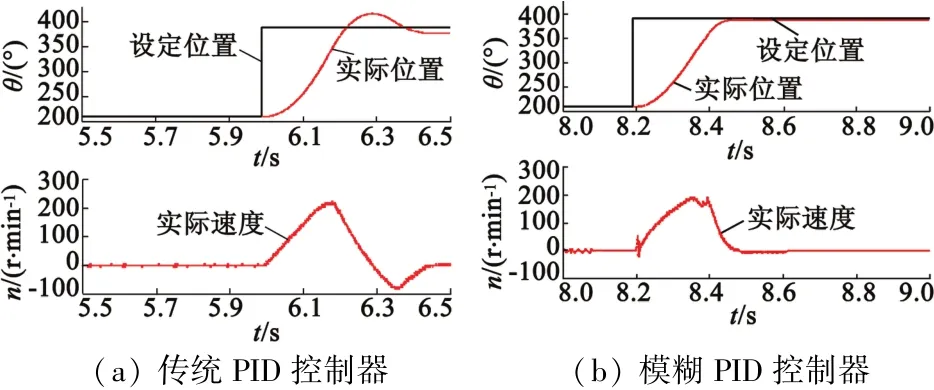
图10 正向电动模式(180°~360°)的响应
从图10可以看出,由于重力作用,传统PID控制器的建立时间约为0.21 s,而模糊PID约0.25 s,与0°~180°转动时基本相同。这个对比结果说明了模糊PID控制器对重力具有较好的鲁棒性。另外,从图10(b)中可以看出模糊PID控制器没有明显的过冲现象,稳定性较好。
5 结 语
本文采用了一种基于模糊PID的BLDC转速控制系统,用于垂直旋转单连杆机器人的位置控制。在机器人控制系统中的位置控制和电流控制模块中采用了模糊PID技术,以此通过调节电机转速实现对机械臂位置的精确控制,并对由机械臂重力引起的转矩变化具有鲁棒性。仿真和实验结果都证明了该系统的可行性和有效性,具有较高的实用价值。
[1]周里津.清洗机器人无刷直流电机驱动系统的设计[D].武汉:武汉理工大学,2012:12-13.
[2]张钊,郭亮.层叠绕组式磁悬浮永磁直流平面电机PID控制系统研究[J].浙江理工大学学报,2014,31(9):525-531.
[3]SUVILATH S,KHONGSOMBOUN K,BENJANARASUTH T,et al.IMC-based PID controllers design for a two-links SCARA robot[J].2011,58(11):1030-1034.
[4]徐敬召,李声晋,卢刚,等.基于模糊PID算法的双闭环电机伺服系统设计[J].微特电机,2013,41(10):40-43.
[5]梁娟,赵开新,陈伟.自适应神经模糊推理结合PID控制的并联机器人控制方法[J].计算机应用研究,2016,33(12):3586-3590.
[6]ALASSAR A Z,ABUHADROUS IM,ELAYDIH A.Comparison between FLC and PID Controller for5DOF robotarm[C]//International Conference on Advanced Computer Control.2010:277-281.
[7]张涛,杨振强,王晓旭.应用eQEP及编码器测量电机位置与速度的方法[J].电气传动,2011,41(4):48-51.
[8]张琪琪,储春华.基于神经网络模糊PID的步进电动机控制系统[J].微特电机,2015,43(8):90-94.
[9]PRIYA K,KUMAR C S.A comparative analysis of PI and fuzzy logic speed control in BLDC motor[J].International Journal of Applied Engineering Research,2015,10(20):15885-15889.
[10]BEGUM A Y,MARUTHEESWAR G V,SWAMY K A.tuning of pid controller for superheated steam temperature system using modified zeigler-nichols tuning algorithm[J].International Journal of Engineering&Advanced Technology,2013,24(5):541-543.
[11]焦军武,卢刚,李声晋,等.模糊PID算法在电动执行器控制系统中的应用[J].微特电机,2014,42(6):55-57.
[12]王万良,石浩,李燕君.基于Mamdani型模糊推理的加权质心定位算法[J].计算机科学,2015,42(10):101-105.

