一种高效的PMSM无位置传感器I/f控制方法
张乘玮,沈汉林,唐其鹏,沈安文
(华中科技大学,武汉430074)
0 引 言
永磁同步电机(以下简称PMSM)具有效率高、动态响应快、转矩惯量比高、功率密度大等诸多优异的性能,在工业、农业和国防领域中得到了广泛的应用。
由于PMSM的无位置传感器控制方式能够减化系统的硬件结构,提高系统的可靠性,近年来得到了国内外学者的较为深入的研究。在低速阶段,常用的方法是通过高频信号注入法[1]获取转子角度信息;在中高速阶段,有滑模观测器法[2-3]、磁链观测器法[4]、扩展卡尔曼滤波器法[5]等,这些方法很难兼顾低速和高速时PMSM位置和速度的有效估算,因此通常需要将这些方法结合起来使用,这不可避免地带来了算法的切换问题,在很大程度上增加了算法的复杂程度和实现难度。
另外在风机、压缩机、水泵等应用领域,由于负载特性相对来说比较固定,往往对系统的动态响应要求不高,通过V/f或者I/f控制方案就能满足要求。针对开环的V/f和I/f控制存在的控制曲线难以规划、负载突变时易失步、效率低等问题,许多学者提出了改进的方法[6-11]。文献[6]利用电机的有功功率的高频分量来调节电压矢量的旋转频率,用来增加系统的阻尼转矩,通过简化的小信号模型分析证明了这种控制方法的稳定性,解决了开环V/f控制在高速阶段运行不稳定的问题。文献[8]利用有功功率的变化量来调节电压矢量的转速、利用功率因数角来动态调节电压矢量的幅值,实现高效稳定的V/f控制。文献[9]提出了一种基于功率观测的电压矢量幅值调节算法,使电机运行在每安培电流最大转矩输出状态(以下简称MTPA),有效地提高了系统的效率,但系统的动态性能则没有明显的提高。
在电机起动或低速运行阶段,由于电机的反电动势较小,不能忽略定子电阻的压降,使用V/f控制时要对电阻压降进行补偿,否则很容易出现失步故障造成无法起动。而当负载大小不确定时,很难规划定子电阻压降的补偿量,导致V/f控制下电机起动困难、低速阶段运行不稳定。另一方面,由于开环的I/f控制能够输出稳定的转矩,并且起动过程电流可控,避免产生了过流故障,当起动电流的大小选取合适时,能够在一定范围内响应负载的振荡变化,因此I/f常用作电机起动阶段的控制方法。为实现电机全频段的I/f控制,文献[10]通过电机有功功率的扰动分量反馈到电流矢量的旋转速度上,用以提高系统的阻尼,但文中的I/f曲线不能进行动态的调节。文献[11]利用电机的瞬时功率来调节电流矢量的频率和幅值,但电流幅值调节过程中使用了无功功率与输出电流的比值,有可能会出现较大的波动而出现振荡。
本文在以上文献的基础上,提出了一种改进的高效永磁同步电机I/f控制方案,文中使用了两个反馈环节:基于有功功率高频分量的电流矢量转速调节闭环;基于电流矢量与q轴夹角的电流幅值调节闭环。在 MATLAB/Simulink平台上的仿真和PMSM样机上的实验表明,所提出算法能显著提高系统运行效率和抗负载扰动的能力。
1 开环I/f控制数学模型
开环I/f控制工作在电流闭环、速度开环状态,一般选取以电流矢量定向的γ-δ坐标系,如图1所示,δ轴方向和电流矢量I方向保持一致,电压矢量U与电流矢量I的夹角记为δ,电流矢量I与实际q轴的夹角记为φ。

图1 坐标系定义
以转子磁链定向的d-q坐标系下的电压方程:

式中:vd和vq代表d轴和q轴电压;id和iq表示d轴和q轴电流;Rs,Ld,Lq分别表示定子电阻、d轴电感和q轴电感;ωr是转子的电角速度;Ψm是永磁体磁链,p为微分算子。
由于δ轴与q轴之间的夹角为φ,可得δ-γ坐标系下的电压方程:

式中:vγ,vδ分别表示γ轴和δ轴的电压;iγ,iδ分别表示γ轴和δ轴的电流;ωi为电流矢量的角速度。因为γ-δ坐标系是以电流矢量定向的,所以iγ=0,式(2)可简化为式(3):
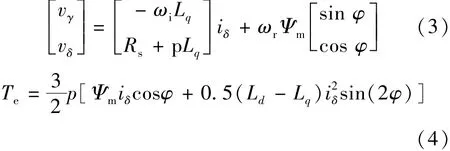
式(4)是γ-δ坐标系下的电磁转矩公式,式中p为电机极对数。
2 I/f控制改进方案
为提高系统的效率和动态响应能力,所提出的改进I/f控制引入两个反馈环节,分别对电流矢量的转速和幅值进行调节。整体的控制框图如图2所示,图中的I*δ为初始电流给定,根据起动负载的大小选取一个合适的值,电机就能够比较稳定地完成起动过程。ω*i是电机的参考运行电角速度,通常要经过一个升降速时间函数的处理,避免参考频率发生突变而产生失步故障。角度θ通过对电流矢量的角速度ωi进行积分得到,由坐标系的定义可知θ角也是γ轴与A相绕组之间的夹角,用来进行坐标变换。Vdc是逆变器的母线电压。
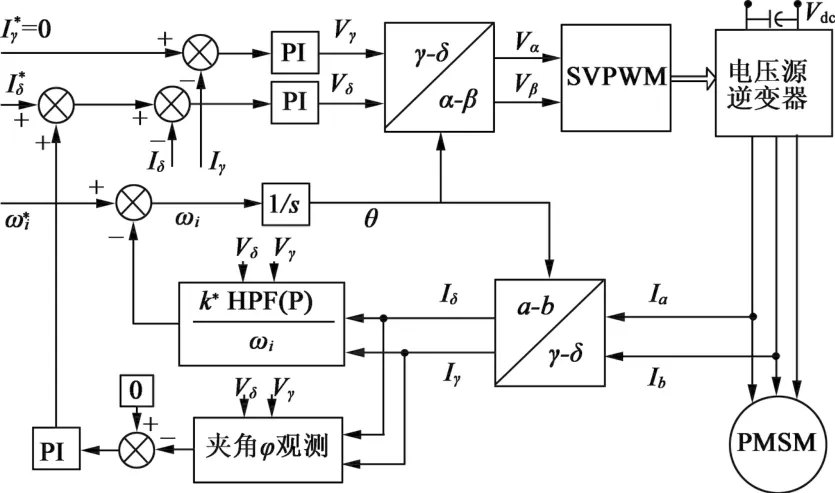
图2 所提出改进方案的整体框图
改进方案包括两个方面:利用有功功率的扰动分量调节电流矢量的频率,以增加系统的阻尼转矩分量。利用电流矢量与q轴之间的夹角φ来调节电流矢量的幅值,以提高系统的运行效率。
2.1 电流矢量频率反馈算法
对于没有阻尼绕组的电机,运行在开环I/f控制时,由于系统阻尼转矩较小,在负载发生突变时很容易失步而产生故障,需要从控制算法上给系统增加必需的阻尼,以提高系统的抗扰动能力。通常通过有功功率的扰动分量来补偿,这一点在文献[6],[7],[11]中进行了比较详细的分析,这里只作简要的叙述。
可以通过对旋转电流矢量增加一个与转子波动量成比例关系的分量,来增加系统的阻尼转矩:
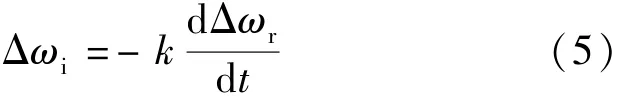
式中:系数k的值与运行频率成反比:

由反馈量Δωi所产生的电磁转矩如式(7)所示,可知ΔTe与转子转速的变化方向相反,起到增加系统阻尼转矩的作用。
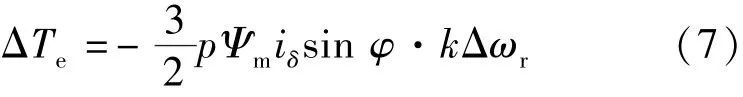
由于电机的实际转速未知,可通过电机的输入有功功率Pe的扰动量来实现电流矢量转速调节:

式中:HPF()表示高通滤波器。
2.2 电流矢量幅值反馈算法
普通开环I/f控制,其I/f控制曲线是由负载的特性离线设置好的,无法根据运行中负载的大小动态调节输出电流矢量的幅值,在负载发生突变的时候由于算法中没有附加的阻尼转矩补偿,电机很容易出现失步而造成停机,严重的情况下系统会失控而损坏功率模块,因而其适用性比较差。
本文所提出的方案是根据计算得到的电流矢量与q轴之间的夹角φ,经过PI调节器反馈到电流矢量的幅值给定,反馈调节框图如图3所示。对于表贴式PMSM来说,可以调节角度φ为0,即电流矢量的方向与永磁体磁链的交轴重合,达到MTPA的控制效果。
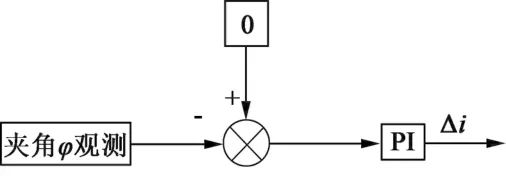
图3 电流矢量幅值调节框图
而对于内嵌式PMSM,其Ld,Lq一般不相等,每安培电流最大转矩状态下的夹角φ不为0,可利用

可利用图3的PI调节器使夹角φ收敛到此值。
各向量之间的关系如图4所示,U是电机的输出电压,忽略逆变器的损耗,可以用vγ和vδ来近似计算。E0是电机的反电动势,R是电机相电阻,Xd和Xq分别表示d轴和q轴电抗。
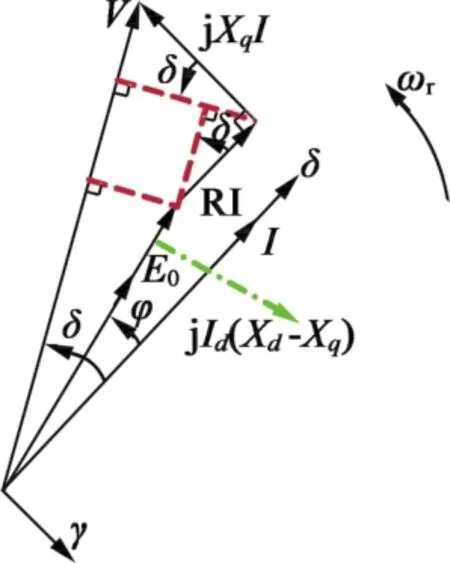
图4 矢量相位图
瞬时有功和无功功率通过vγ,vδ,iγ和iδ计算得到:

它忽略了逆变器的开关损耗。电机的功率因数角,即电流矢量与电压矢量的夹角δ,可利用瞬时无功功率Q和有功功率P来计算得到:

由于γ-δ坐标系是以电流矢量的方向定向的,所以iγ为0,有功和无功功率的计算可以简化为式(10)和式(11)。反电动势E0与q轴的方向重合,根据各矢量之间的关系,可以得到夹角φ,如式(13)所示。值得注意的是,式(13)是基于稳态时得到的角度关系,式中的Xq与电机的转速有关,由于电机的实际转速无法得到,计算时以电流矢量的旋转频率Δf代替,如下:

不同于其它转子角度和速度的观测方法,式(13)所表示的夹角φ的计算过程中不含有任何低通或带通滤波器,没有相位的延迟,也因此有着更快的动态响应。
为了使夹角φ更快地收敛到设定值,可以在夹角φ与参考值差别过大时,适当提高PI调节器的参数,以加快响应,提高系统的动态性能。
3 仿真和实验验证
为了对本文所提出的高效I/f控制方法进行验证,分别在MATLAB/Simulink仿真平台和8.3 kW PMSM实验平台上进行了实验,仿真和实验中所用电机的参数如表1所示。

表1 表贴式PMSM的参数
3.1 仿真分析
由于坐标系是以电流矢量定向的,即电流矢量I与α轴的夹角已知,由式(13)可以得到电流矢量I与实际q轴之间的夹角φ,由此可以得到观测的q轴的位置,图5给出了在50 Hz频率运行时实际q轴位置和利用式(13)观测到的q轴位置的仿真波形,可以看出这两者之间的误差很小。
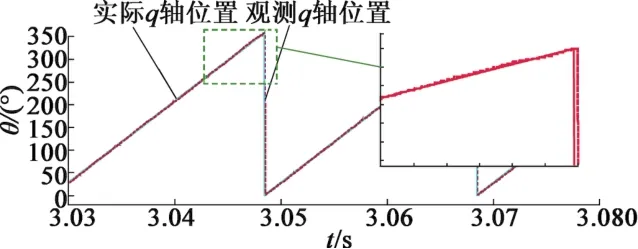
图5 50 Hz运行时实际和观测q轴位置
为验证所提出的改进方案在负载发生突变时的转速收敛性能,给出在额定频率(100 Hz)下负载变化时的仿真波形。如图6所示,在第5 s左右负载由2 N·m突变到20 N·m,在第7.6 s左右由20 N·m突变到40 N·m。由仿真波形可知,负载发生突变时,电机的转速和输出转矩会出现短暂的振荡,然后电机恢复了稳定运行。由观测到的电流矢量I与q轴之间的夹角φ的波形可知,经过短暂的调节之后夹角φ收敛到了0附近,即电机的d轴电流也调节到了0附近,达到了MTPA的运行状态。

图6 负载突变时的仿真波形
作为对比,图7给出了在额定频率(100 Hz)下普通开环I/f控制的仿真波形。电流幅值恒为10 A,从零速加速到100 Hz用时2 s,3.6 s之前负载转矩恒为2 N·m,可以看出,当负载较小而电流矢量幅值偏大时,电流矢量与q轴的夹角φ是较大的,即实际d轴电流所占比重较大,导致系统运行效率低下。在3.6 s时负载突变为20 N·m,可以看出电机转速急剧下降,发生失步故障,系统的稳定性较差。由于仿真中所加的负载为反向转矩,所以失步后电机开始往反方向旋转。
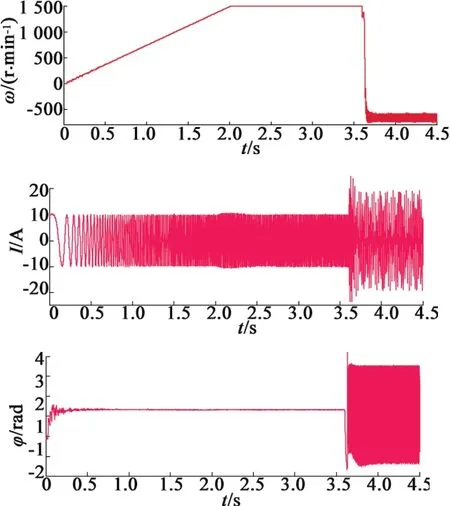
图7 开环I/f控制的仿真波形
3.2 实验验证
本文对表1中的表贴式PMSM进行了实验,对应电机型号为海天伺服电机HS1804152R-F,利用Wi-Fi上位机监控软件记录数据。
首先进行了50%额定频率运行时负载突变的测试,负载在4.0 s时从0突变到40%额定负载,9 s时从40%突变到80%额定负载,12.5 s时从80%突减至40%额定负载,15.5 s时从40%突减至0,电机的转速和A相电流波形如图8所示。

图8 50 Hz运行时负载突变实验波形
然后进行了在100%额定频率时负载突变的测试,负载在3.5 s时从0突变到60%额定负载,7.2 s时从60%突变到100%额定负载,12.8 s时从100%突减至60%额定负载,17.5 s时从60%突减至0,电机的转速和A相电流波形如图9所示。
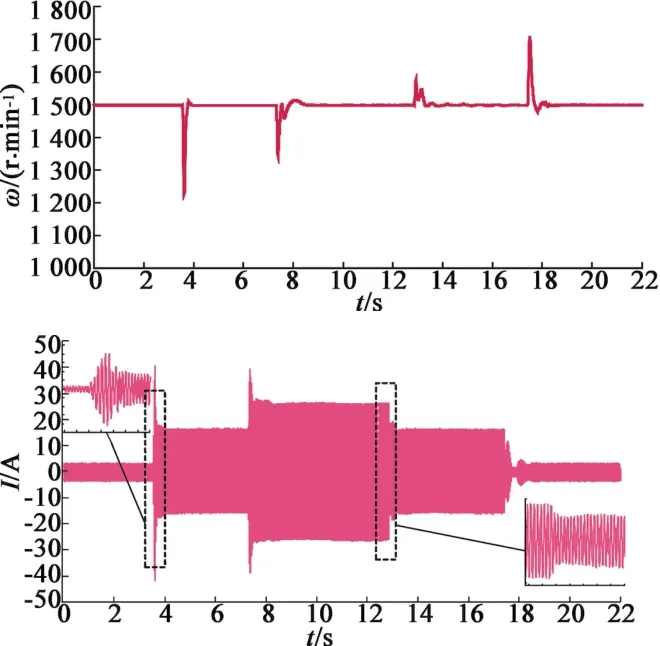
图9 100 Hz运行时负载突变实验波形
由图8和图9可以看出,所提出的改进I/f方案在负载发生较大的突加和突减变化时,经过短暂的调整,电机转速能够快速地收敛至给定运行速度,输出电流矢量的幅值能够跟随负载的大小而实时调节,使系统始终运行在MTPA状态。
4 结 语
PMSM的I/f控制由于电流可控、输出转矩较为稳定,常被用作无位置传感器控制起动阶段的控制方法。本文针对开环I/f控制存在的问题,介绍了一种改进的高效I/f控制方法,利用有功功率的高频分量对旋转电流矢量的频率进行补偿,利用观测所得的电流矢量和q轴的夹角来对电流矢量的幅值进行调节。结果表明所提出的改进方案在稳定性和运行效率方面优于普通开环I/f控制。
[1]鲁家栋,刘景林,卫丽超.永磁同步电机转子初始位置检测方法[J].电工技术学报,2015(7):105-111.
[2]陆婋泉,林鹤云,冯奕,,等.永磁同步电机无传感器控制的软开关滑模观测器[J].电工技术学报,2015(2):106-113.
[3]张润波,林荣文,高靖凯.基于改进滑模观测器的PMSM无位置传感器的研究[J].电气技术,2016(1):51-54,61.
[4]王斌,王跃,郭伟,王兆安.基于定子磁链降阶状态观测的永磁同步电机无差拍直接转矩控制系统[J].电工技术学报,2014(3):160-171,195.
[5]QUANGN K,HIEU N T,HA Q P.FPGA-Based Sensorless PMSM Speed Control Using Reduced-Order Extended Kalman Filters[J].IEEE Transactions on Industrial Electronics,2014,61(12):6574-6582.
[6]PERERA PD C,BLAABJERG F,PEDERSEN JK,etal.A sensorless,stable V/f controlmethod for permanentmagnet synchronous motor drives[J].IEEE Transactions on Industry Applications,2003,39(3):783-791.
[7]TANG Z,LI X,DUSMEZ S,et al.A new V/f-based sensorless MTPA control for IPMSM drives[J].IEEE Transactions on Power Electronics,2016,31(6):4400-4415.
[8]ANDREESCU GD,COMAN C E,MOLDOVAN A,etal.Stable V/f control system with unity power factor for PMSM drives[C]//Optimization of Electrical and Electronic Equipment(OPTIM),2012 13th International Conference on,Brasov,2012:432-438.
[9]张幸浩,章玮.一种基于功率观测的永磁同步电机高效V/f控制[J].机电工程,2015(4):516-520,530.
[10]BORISAVLJEVIC A,POLINDER H,FERREIRA JA.Realization of the I/f controlmethod for a high-speed permanentmagnetmotor[C]//Electrical Machines(ICEM),2010 XIX International Conference on,Rome,2010:1-6.
[11]王萌,杨家强,张翔,等.一种表贴式永磁同步电机电流矢量闭环I/f控制方法[J].中国电机工程学报,2015(10):2513-2521.

