基于问题驱动的方向导数性质探讨

陈佩树，马松林，彭维才

(巢湖学院 应用数学学院，巢湖 安徽 238000)

基于问题驱动的方向导数性质探讨

陈佩树，马松林，彭维才

(巢湖学院 应用数学学院，巢湖 安徽 238000)

方向导数是多元函数微分学中一个重要概念，首先给出方向导数定义，接着以问题驱动方式对方向导数性质进行剖析和探讨，深入分析方向导数与偏导数、可微、梯度、沿给定方向单调性等有关概念之间的关系。

问题驱动; 方向导数; 偏导数; 可微

0 引 言

方向导数既属于高等数学基本理论知识，[1-2]也是许多理工类专业必不可少的一个重要应用工具。方向导数是多元函数微分学的一个重要概念，其本质上是研究函数在某点处沿某一指定方向的变化率问题，是偏导数知识的拓展，在研究函数局部性质和解决许多实际应用问题中都有着重要作用。

1 方向导数定义

2 问题驱动式探讨方向导数性质

问题1 若函数f在点P0的沿任一方向的方向导数都存在，能否说明f在点P0偏导数存在？能否说明f在点P0可微？

仔细剖析方向导数的定义会发现： 即使是沿x轴正向、 负向两个方向导数分别存在，但无法确定其数值一定相等，所以依然可能偏导数不存在,也无法确保函数f在点P0可微。[3]

例1 函数f(x,y,z)=(x2+y2+z2)1/2在点(0,0,0)有

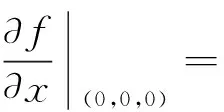
从而可知f(x,y,z)=(x2+y2+z2)1/2在点(0,0,0)关于x的偏导数不存在，同理可知在点(0,0,0)关于y或z的偏导数也不存在，故函数在点(0,0,0)也不可微。

问题2 若函数f在点P0的偏导数存在，能否断定f在点P0的方向导数也存在？

从偏导数定义出发，可以知道关于x轴的偏导数存在，仅能确保沿x轴正、负两个方向的方向导数分别存在，无法确定沿任一给定方向的方向导数也存在。下面通过案例加以说明。

显然以上极限不存在，也就是说在该点沿任意方向的方向导数不存在。

问题3 如果多元函数f在点P0可微，是否可以确保此函数在给定点沿任意方向的方向导数存在？如果存在，能否找到在给定点的最大(小)方向导数？

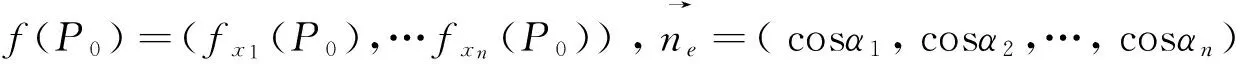
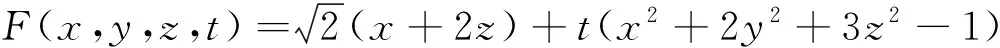
问题4 能否利用方向导数探讨函数沿任意给定方向的单调性及函数极值问题？

例4 试证明当x+y+z≠0时，有ex+y+z>x+y+z+1成立。

证明 构造辅助函数f(x,y,z)=ex+y+z-x-y-z-1，于是有f(0,0,0)=0。

当x+y+z>0时，有(ex+y+z-1)(x+y+z)>0;

当x+y+z<0时，也有(ex+y+z-1)(x+y+z)>0。

3 结束语

方向导数是多元函数微分学中在偏导数、函数微分概念之后，另外一个非常重要的基本概念。本文以问题为导向，从偏导数的概念很自然地引出方向导数在n元函数上的概念。 在某点偏导数存在仅能表明在此点沿某个给定坐标轴方向的方向导数存在，但不能保证沿其他方向的方向导数也存在；在某点任意方向的方向导数存在可以确保在此点沿着坐标轴正、反两个方向的方向导数都存在，但是不能断定它们存在且相等；函数可微可以确保方向导数和偏导数都存在，但反之不成立。另外，通过方向导数探讨了多元函数沿任意给定方向的单调性及极值问题。

[1] 同济大学数学教研室．高等数学：下册[M]．6版.北京：高等教育出版社，2007：101- 107．

[2] 华东师范大学数学系.数学分析：下册[M].4版. 北京：高等教育出版社,2010：133- 135.

[3] 陈春梅,屈娜,王正元.问题驱动式教学方法在方向导数教学中的应用[J].数学学习与研究，2013(4):13- 14.

[4] 马烁, 梁向. 基于方向导数的多元函数极值的判定[J]. 长江大学学报(自然科学版), 2016, 13(22):64- 67.

[责任编辑：张永军]

Research about Directional Derivative Properties Based on Problem Driven

CHEN Pei- shu, MA Song- lin; PENG Wei- cai

(School of Applied Mathematics, Chaohu University, Chaohu 238000，Anhui,China )

Directional derivative is one of the most important concepts in differential calculus of pluralistic functions. In this paper, the concept of directional derivative is introduced, explained and deeply analyzed by problem- oriented approach. The relationship between the directional derivative, the partial derivative, differentiable functions, and monotonicity are also studied by examples.

problem driver;directional derivative;differentiable function

2016-10-15

2017-02-20

省质量工程项目(2015jyxm324,2016jyxm0689, 2016jyxm0691)、大学数学教学团队项目(ch12td01)、巢湖学院质量工程项目(ch16kcjgxm22,ch16yykc07, chxy15yykc03, XLY-201301)资助。

陈佩树(1979—)，男，安徽来安人，巢湖学院应用数学学院副教授、博士，研究方向：运筹学。

O143

A

2096-2371(2017)02-0012-04