精心备课，提升数学课堂效率

朱叶青

【摘 要】有特色的知心数学课堂，它的教学的有效性往往取决于课前的精心备课，所谓的效果显课堂，功夫在课前。本文结合笔者的数学教学实践对如何生成特色知心数学课堂进行了探讨。

【关键词】知心；特色；备课；磨课

当前，课堂上的“特色，知心”这一严峻课题又摆在了每一位师生面前。既要特色又要知心，这是我们师生所期盼的最高境界。教材的不断更新，内容的不断加深，课堂教学目标设定的不科学，课外辅助教材的随意拔高，让教师、学生和家长都逼入了误区，在教学实践中往往把握不住分寸。然而仁者见仁，智者见智，现就“特色知心课堂”这一话题，以笔者所教的数学学科为例，细说如下。

一、如何理解有教学特色的知心数学课堂

什么样的数学课堂最受欢迎、最高效？答案应该是：有教学特色的知心数学课堂。教学特色，主要是指教师在教学中表现出来的独特教风。它包括教师的气质、仪表、语言、教学方式和方法等方面的与众不同之处，是教师长期探索、研究、涵养，水到渠成的一种自然表现，而绝不是东拼西凑、刻意苛求出来的矫揉造作。学生能够从富有特色的知心教学中，感受到学习的无穷乐趣、知识的无尽浩渺、人格的特有魅力，并令人神往。知心指的是体验别人内容世界的能力。“知心”的重点在一个“情”字，一个“理”字。知心课堂应该是有情有理，“情”与“理”融为一体的课堂。良好的师生关系对学习质量的影响，只有情感才能唤醒情感，教育是人与人之间心灵的沟通，是人的精神的生长和充盈。亲其师，才能信其道，只有“知心”才能建立和谐融洽的师生关系，才能快乐的学习，更快的进步。作为一名教师，与学生沟通是一门学问，在师生的交往中要少用情绪，多用智慧。在教育教学的过程中，教师站在学生的角度，感受学生的喜怒哀乐，不把自己的价值观强行地加在学生的身上，设身处地地理解学生，体验学生的真实内心世界，让学生充分地感受到自己被理解和接纳，以此促进师生间的沟通交流，建立和谐的师生关系。通过知心数学课堂的设计与应用，教学过程中体现教师与学生一起共同学习，实现共情，教学相长，从而达到共同发展。

具有教学特色的知心数学课堂的形成非一朝一夕之功，他凝聚着教师锲而不舍的心血。一位著名教师這样形容：一个教师要形成有特色的教学风格，要有坚实的专业知识。如果没有厚实的专业知识积淀，是不可能在教学中厚积薄发、左右逢源的；也不可能创造性地开展教学工作，形成自己的教学特色。

当然，不同教师、不同的教法会产生不同的教学效果，甚至在对学生的人生影响方面也会有天壤之别。特色、知心，正是有效教学最关注的问题，也是教师显示个性和才能的关键所在。

二、如何体现效果显课堂，功夫在课前

既然，特色教学的知心课堂如此重要，那么如何形成自己的教学特色的知心课堂？今天我着重从备课说起：课堂教学的有效性往往取决于课前的备课。我们要明确：效果显课堂，功夫在课前。

当今，教师的备课存在着几种无特色、无知心现象：

一是大部分教师抄教案，抄教参；

二是“翻新工程”，老的教案改改弄弄变新的；

三是网上直接照搬下载教案。

由于抄备课现象的存在，教师不能好好钻研教材，导致教师对教材的解读不到位。如果老师自己都对教材的解读有偏颇，都不到位，那么课堂教学的定位肯定是不恰当的，目标肯定是不明确的。这样的备课，教师根本没有去了解学生，研究教材，甚至抄了些什么内容都无从知道。上课拿着课本轻装上阵，教学效果可想而知了。教师由于没有好好地去钻研教材，缺少对整个教材整体的把握，理解不透，不知道这一课教学内容在整个一册教材体系中处于什么地位，那么往往对教学目标的确定是很模糊的，对重难点的把握更是难上加难了。这样一来，就会造成这样的现象：上课时，就像脚踩西瓜皮，上到哪里就算哪里，这样就忽略重要环节的设计，难点就难以突破，必然会造成重复累赘。“拖堂” 现象很大比例上是由于备课不充分造成的，而“拖堂”是课堂教学效能低下的直接表现。因此，这样不动脑子琢磨推敲，只动手抄写的“徒手教案”，很难生成精彩的课堂。

备受推崇、令人回味的好课，往往在学生探索新知识的过程中有新颖别致的精妙设计，让人豁然开朗、眼前一亮：“原来课还可以这样上。”

下面列举一堂特色知心数学课堂的备课过程中的磨课思路：

内容：八年级下册，6.1矩形第三课时。

这节课是继前面两课时学习了矩形的定义、性质和判定之后，对上述知识综合复习、应用的一节课。

（一）初始设计

本节课只安排了一个例题，“证明定理：直角三角形斜边上的中线是斜边的一半”，教材所安排的练习也大都是围绕着这一性质定理的应用来设置，因此，沿用教材的设置，按“回顾矩形性质与判定-应用性质证明-应用所证得的定理” 的环节来设计。但发现：这样的设计没能很好的理解教材的本意，容易会变成一节“炒冷饭”的课，学生也不爱听，更不能很好的对前面所学的矩形的知识进行巩固和应用。由此，考虑从课本所安排的例题着手拓展来进行教学设计，力求能突出教材安排本节课的意图，即本节课的主题——矩形知识的综合运用.

（二）二次设计

思考：教材中的证法为什么选用三角形旋转变换的方法来构造平行四边形呢？

理解：教材的意图是应用平行四边形的中心对称性来解决这个问题，突出平行四边形的一个本质的图形性质——中心对称性。事实上，平行四边形的所有性质都是可以用中心对称性来解释的，而平行四边形的形成，最初也是由三角形关于一边的中点做中心对称而形成的。“三角形中位线定理”的另外两种证法也是受此启发来另外添加辅助线构造平行四边形。基于以上的认知基础和解决问题的经验，既然矩形是特殊的平行四边形，那学生应该也可以基于其图形本质的属性——中心对称性来构造矩形。只不过要做的是，做好铺垫，引导学生捅破这层“窗户纸”，寻根溯源，回归数学的本质，图形的本质。

基于以上的考虑，做了如下的铺垫与设计：

（1）若用如图放置的两个全等直角三角形拼矩形。

①需将△ABC做怎样的变换才可以与△DEF拼成一个矩形？

②请在△DEF的基础上画出所拼出的图形，并说出所拼出的图形是矩形的理由？

（设计意图：引导学生经历矩形的形成过程，对于矩形的构造有一个直观的体验.既对矩形的中心对称性作进一步的认识，也顺带复习矩形的定义与形状，引导学生从矩形的本质属性中感受性质，从另一个不常见的角度来解读矩形。）

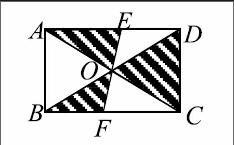
（2）如图，矩形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD和BD于点E，F，AB=2，BC=3，则图中阴影部分的面积为 .

（设计意图：进一步的让学生感受灵活运用中心对称性的优越性。）

（3）证明定理“直角三角形斜边上的中线是斜边的一半”。

（设计意图：通过上面两题的铺垫，使运用中心对称性来构造矩形的方法水到渠成。）

问1：可以通过什么方法来构造矩形？你是依据什么想到的？

问2：还有什么方法可以构造矩形？以往有什么可以借鉴的经验？

（设计意图：通过不停的寻根溯源，使思维层次不断的深入，体验数学中“类比”与“转化”数学思想，同时也引导学生善于去发现与总结学习的方法与规律，争取做到“授之以渔”。）

同时，还考虑到，矩形是特殊的平行四边形，矩形不仅是中心对称图形还是轴对称图形，从矩形轴对称性的角度是否也可以比较方便的来解决一些较为复杂的题目呢？由此，选取两个以往练习做过综合性比较强的问题来做了一个拓展：

（4）如图，在矩形ABCD中，AB=8cm，BC=6cm，对角线AC和BD相交于点O，点P沿线段AB从A向B运动，运动速度为1cm/s， 当点P运动到OP与△AOB的一边垂直的位置时：

①在备用图中画出满足条件的点P，并标上P1，P2…Pn；

②观察并判断这些满足条件的点P的位置。

答案是

（设计意图：从矩形的轴对称性可知△AOB是等腰三角形，因此，从答案图中可以看出P1与P3关于OP2成轴对称，使学生进一步的感受矩形的轴对称性的合理运用所带来的便利性。）

（5）如图，在矩形ABCD中，AB=8cm，BC=6cm，点P沿线段DC从D向C运动，运动速度为1cm/s，设点P运动的时间为t秒，若以点P，A，B为顶点的三角形为等腰三角形，请求出t的值。

（设计意图：通过上一题的铺垫，对于矩形对称性的灵活运用做一个巩固与提高，让学生体会寻找最优化解题方法的快乐.在不少中考題的压轴题中，多解的问题往往都可以利用对称性。）

（三）拓展与反思

本节课从对称的角度来解读矩形这一特殊的平行四边形，可谓是另辟蹊径，但又没有脱离矩形的知识，反而紧扣矩形的本质属性来研究。

三、形成有特色的知心数学课堂

这节课经过二次磨课，认真备课，形成了一节特色的有韵味的知心数学课，教学效果显然好多了。由此可见，有特色的知心数学课堂是从备课开始的。

因此，备课时应做到：以课例为载体；以课本为根本；以变式为方法；以效率为目标。能把复杂的问题简单化就是完美，能把简单的问题深刻化就是杰出！那我们的课堂一定是精彩的课堂，是备受推崇、令人回味的有特色知心数学课堂。

参考文献：

[1]高慎英，刘良华.有效教学论[M].广州：广东教育出版社，2004.9.

[2]皮连生.学与教的心理学[M].上海：华东师范大学出版社，2009.5.