数学中的习题变式教学——从一道关于三角形内接正方形习题谈起

文/吴卫通

数学中的习题变式教学
——从一道关于三角形内接正方形习题谈起

文/吴卫通

数学教材中例题、习题是数学问题的精华，挖掘其内在的学习线索,对这些题目进行推广与变式教学,能积极培养学生的创造性思维,达成多维目标的过程。现举数学课本中一道习题为例来谈谈变式教学。

如下图，△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?

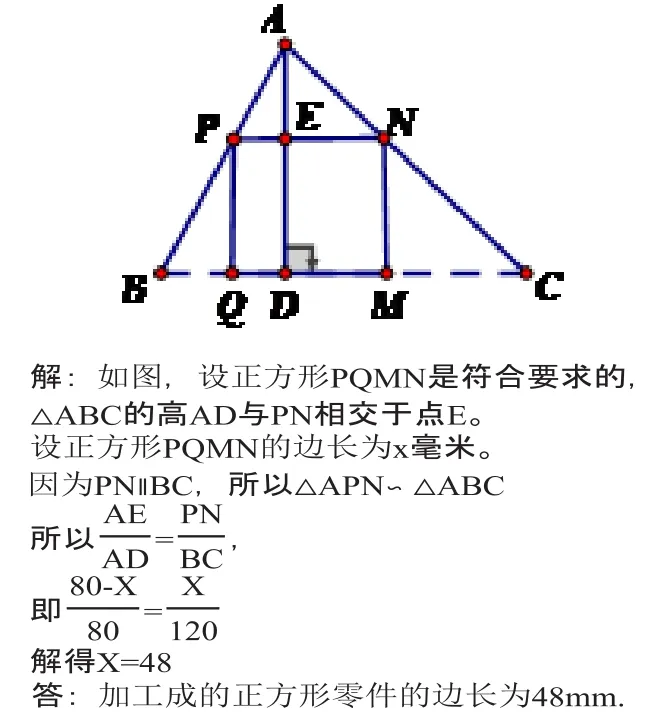
在教学中，笔者将此题做如下变式教学：

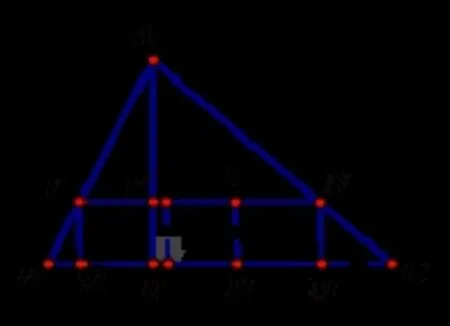
图一

图二

变式1 如图一，如果原题中要加工的零件是一个矩形，且此矩形是由三个并排放置的正方形组成，此时这个零件的两条边长分别是多是mm?

变式2 如图一，如果原题中要加工的零件是一个矩形，且此矩形是由n个(并排放置的正方形组成，此时这个零件的两条边长分别是多是mm?(直接用含n的代数式表示)

生1：上述变式1、2两题根据相似三角形性质即可完成。

变式3 如图二，如果原题中要加工的零件是只一个矩形，求此时这个矩形零件面积的最大值是多少mm？

生2：设矩形宽PQ=xmm,面积为ymm2,由相似性质求得PN= ，得y= ，再根据二次函数性质求得最大值。

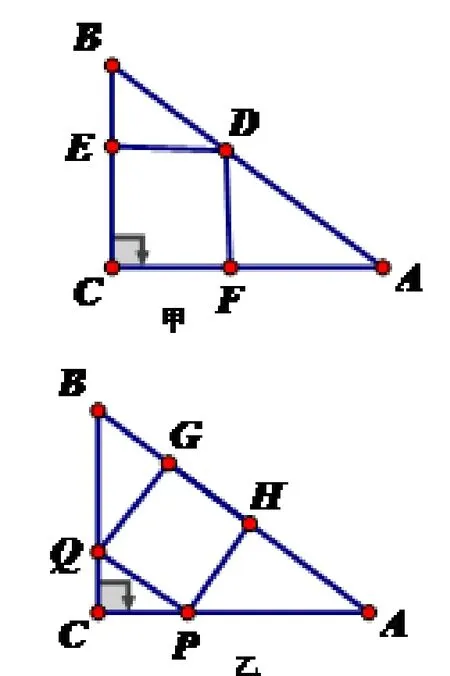
图三

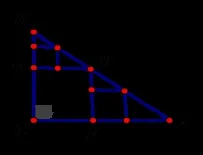
图四

变式4 如图三，有一块三角形余料，∠C=90°，AC=8cm,BC=6cm。要在这块余料中剪出一个尽可能大的正方形，有甲乙两种剪法，比较两种剪法，哪种剪法所得的正方形面积大，请说明理由。

生3：甲乙两种剪法都可根据相似三角形性质求得。

变式5 如图四，图三中甲种剪法称为第一次剪取，记所得的正方形面积为s1；按照甲种剪法，在余下的△ADF与△BED中，再剪出两个正方形，称为第二次剪取，并记这两个正方形面积和为s2,则s2=。

生4：根据相似三角形性质求得。

变式6 师：对任意一个三角形，其内接正方形共有几个呢？

生5：要根据三角形形状分类讨论。

生6：当三角形为锐角三角形时，有3个内接正方形；当三角形为直角角三角形时，有2个内接正方形；当三角形为钝角三角形时，有1个内接正方形。

师：再把有关”内接正方形问题“与函数等知识相结合，达到延伸拓展目的。

变式7 在平面直角坐标系中，将n个边长为1的正方形并排组成矩形OABC，相邻两边OA、OC分别在x轴和y轴正半轴上，设抛物线y=ax2+bx+c(a<0)过矩形顶点B、C。

（1）当n=1,如果a=-1,求b的值；

（2）当n=2,在矩形OABC上方作一个边长为1的正方形EFMN，使EF在线段BC上，如果M、N两点也在抛物线上，求出此时抛物线的解析式；

（3）将矩形OABC绕点O顺时针旋转，使点B落到x轴正半轴上，如果该抛物线同时经过原点O。

当n=3时a的值；

②直接写出a关于n的关系式。

生7：当n=1时，可知抛物线对称轴为直线x=，求得b=1;

生8：当n=2时，把B(2,1),M(C(0,1)带入函数解析式即可求得；

生9：当n=3时，结合相似三角形来解决第（3）题。

总之，教师在教学中要善于“借题发挥”，进行一题多变，引导学生去探索数学问题的规律性和方法，达到“做一题，通一类，会一片”的教学效果，让学生走出题海战术，真正做到轻负高质。

（作者单位：浙江省金华市第十四中学）