基于自抗扰的自适应控制在永磁同步电机控制中的应用
张德民, 徐仕源
(1.天津理工大学 自动化学院,天津 300384; 2.天津市复杂系统控制理论及应用重点实验室,天津 300384)
基于自抗扰的自适应控制在永磁同步电机控制中的应用
张德民1,2, 徐仕源1,2
(1.天津理工大学 自动化学院,天津 300384; 2.天津市复杂系统控制理论及应用重点实验室,天津 300384)
介绍了一种以自抗扰控制理论为基础的自适应控制技术,并通过MATLAB/Simulink建立仿真模型将其应用于永磁同步电机的控制。仿真结果表明,与传统的PI控制器相比,运用此方法后电机转速更加平稳,鲁棒性好,而且系统的控制能量小。
自抗扰控制;永磁同步电机;自适应控制;控制能量
0 引 言
永磁同步电动机(Permanent Magnet Synchronous Motor,PMSM)由电励磁三相同步交流电动机发展而来,具有结构紧凑、高气隙磁通密度、高功率密度、高转矩惯性比和高效率等优点,因而在伺服系统、机器人等领域应用广泛。但是,PMSM是一个多变量、强耦合、非线性、时变的机电系统,传统的PID控制虽然简单,便于应用,但已经不能满足现代工业的高精度、强抗干扰能力等要求。目前,PMSM控制的主要研究方向有:PID与其他现代控制方法的结合[1-2]、鲁棒控制[3]、滑模控制[4-5]、智能控制[6-7]和自抗扰控制(Active Disturbance Rejection Control,ADPC)[8-11]等。本文介绍了一种基于ADRC的自适应控制方法,并设计了PMSM转速自适应ADRC控制器。仿真结果表明,设计的PMSM速度控制器具有抗干扰能力强、鲁棒性好、控制能量小等特点。
1 PMSM的数学模型
在不计电机磁路饱和,忽略磁滞、涡流损耗等理想情况下,PMSM在dq同步旋转坐标系下的数学描述为
(1)
(2)
(3)
(4)
式中:θ——转子位置;ω——转子角转速;p——电机极对数;J——转动惯量;B——摩擦因数;TL——负载转矩;ψf——永磁转子磁链;id、iq,ud、uq——d、q轴定子电流和电压分量;
Rs、L——定子电阻、电感。
2 基于ADRC的自适应控制器
2. 1 ADRC的一般形式

图1 二阶ADRC框图
ADRC[12]是韩京清教授在深入剖析经典PID控制的优缺点后开发出来的一种新型实用的控制技术。ADRC主要由跟踪-微分器(Tracking Differentiator,TD),非线性状态反馈控制律(Nonlinear State Error Feedback,NLSEF)和扩张状态观测器(Extended State Observer,ESO)这三部分组成。二阶ADRC的框图如图1所示。图1中:v0为系统的给定输入;v1为TD的跟踪输出;v2为TD的微分输出;u0为中间虚拟控制量;z1为对输出的观测值;z2为输出微分的观测值;z3为对包括系统内扰和外扰在内的系统总扰动的观测值;b0为扰动的补偿因数,决定着对总扰动补偿的强弱。
2. 2 转速自适应控制
由文献[13]可知,控制量是系统给定值v0的函数u=f(v0),控制的能量则可以用u2=f2(v0)来表示,因此能量最小的控制问题归结为选择函数u2=f2(v0)取最小值的设定值v0的问题,即根据外扰的变化随时调整设定值来使所花的控制能量最小,是一种自适应控制过程。
由式(2)可知,PMSM转速环的动态方程为一阶微分方程,因此,这里用的是一阶ADRC,基于此的自适应算法优化具体如下。
首先,根据速度的设定值v0安排过渡过程,为了避免数字计算时产生高频振荡,这里采用离散化的TD:
(5)
式中:r0——决定TD跟踪快慢的系数,即决定着过渡过程的快慢;
h——积分步长。
然后,根据系统输出来设计ESO:
(6)
其中,fal函数的表达式为
(7)
式中,β01>0,β02>0为可调参数,0<α<1;δ>0,决定了线性区间的大小,这里取δ=h。
形成误差信号e1、误差反馈控制量u0及最终控制量u:
(8)
根据输入-输出关系确定优化所需导数。
把控制量u送入跟踪微分信号TD1来获得u的跟踪信号u1及其微分信号u2:
(9)
把设定值v0送入跟踪微分器TD2来获得v0的跟踪信号v01及其微分信号v02:
(10)
为了避免出现v02为零的情况,需要对v02进行处理:
(11)
这样就可以获得优化所需的导数:
(12)
为了获得比较好的微分信号,使用TD3对d进行滤波处理:
(13)
再对v0修正:

(14)
为了获得好的滤波效果,式(5)~式(13)的fhan中的h可以取h0=kh,k>1,每个式中的k可以不同。
通过以上处理可以设计出一个基于ADRC的速度自适应控制器。
3 仿真试验
为了验证设计的有效性,本文利用MATLAB/Simulink建立仿真模型。仿真系统采用矢量控制的方法,利用上述方法对速度环优化。其结构如图2所示。
图2中,电机模型使用MATLAB/Simulink自带的PMSM模型,其主要参数如下:定子电阻Rs为2 Ω,Lq和Ld均为8.5×10-3H,永磁转子磁链ψf为0.5 Wb,转动惯量J为8×10-4kg·m2,粘滞摩擦因数B为3.035×10-4N·m·s,极对数p为2。

图2 PMSM自适应ADRC框图
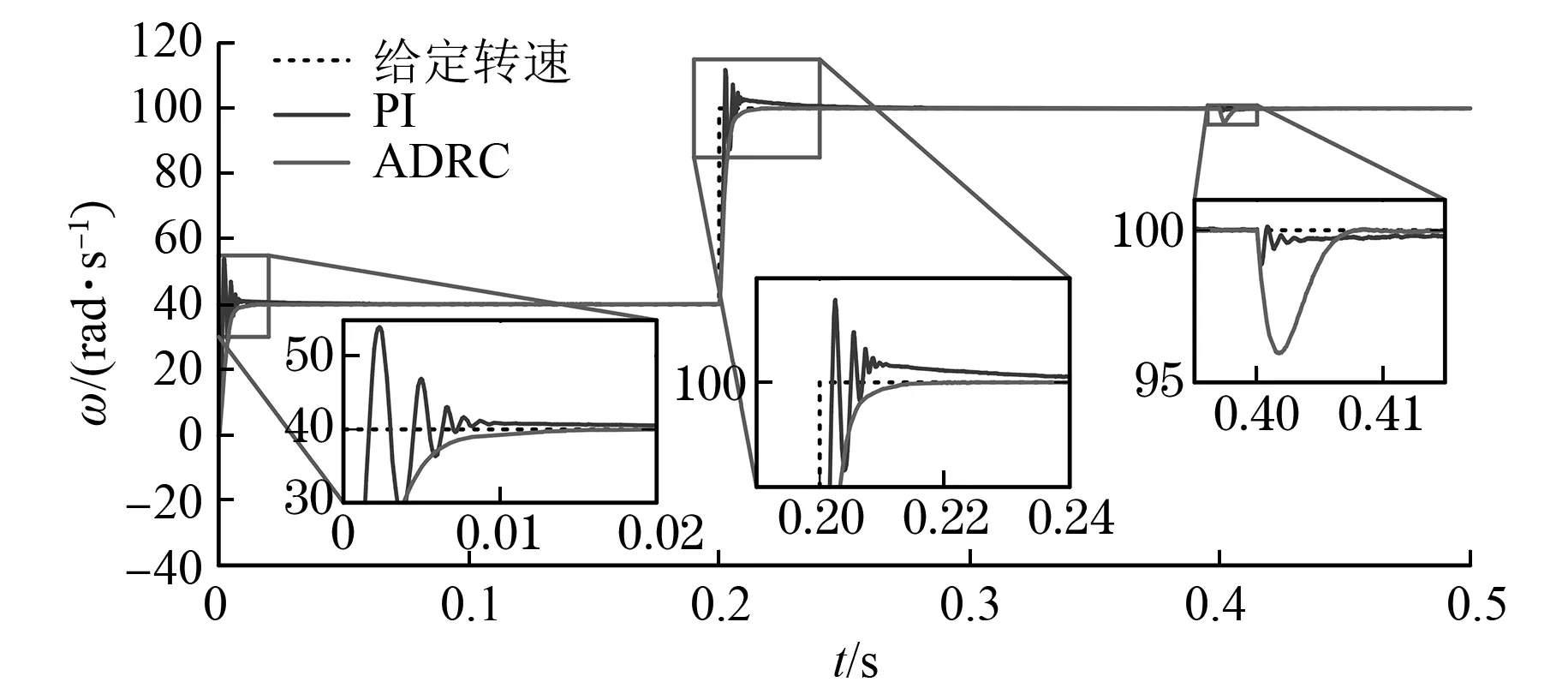
图3 转速响应曲线
图3为电机的转速响应曲线。初始转速给定为40 rad/s,在0.2 s时给定转速突变为 100 rad/s,在0.4 s时负载转矩由5 N·m变为 10 N·m,从响应曲线可以看出,使用上述方法优化后的ADRC,一次无超调地跟上了给定,而PI控制则要经过振荡才进入稳态。值得注意的是,在0.4 s时负载转矩提升,由于ESO的快速响应并给于补偿,使转速产生了一个向下的振动,但在约0.01 s内又进入了稳态。
图4为控制量的曲线,就是速度环控制器给下一级电流PI控制器的控制量。由图4可看出无论是初始响应还是当给定速度和负载发生变化时,ADRC的控制量始终很小,并且变化不大。
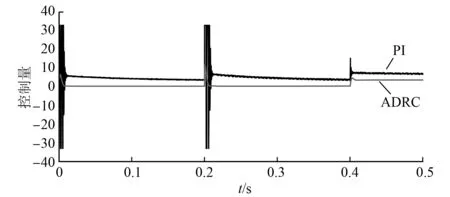
图4 控制量曲线
图5为定子三相电流响应曲线。由图5可看出,使用自适应ADRC时,当转速给定和负载转矩发生变化时,定子三相电流波动更小,而使用PI控制时,定子三相电流经过多次振荡才进入稳态。

图5 电流响应曲线
4 结 语
ADRC具有不需要精确的系统模型、抗干扰能力强及鲁棒性好等优点,将其运用于非线性、强耦合、多变量的PMSM控制中取得了非常好的效果。介绍了一种基于ADRC的自适应控制技术,并设计了电机转速环的自适应ADRC,可以看出这种控制方法不仅具有ADRC抗干扰能力强、稳定性好等优点,而且还具有最优控制的特点,控制能量小。
[1] 张伦健,陈利萍.基于智能PI的永磁同步电动机近似最大转矩电流比控制[J].微特电机,2012,40(8): 42-45.
[2] 郭卫杰,刘维亭,林永才.智能PI算法在永磁同步电动机控制系统中的应用[J].微特电机,2011,39(3): 34-37.
[3] 杨书生,钟宜生.永磁同步电机转速伺服系统鲁棒控制器设计[J].中国电机工程学报,2009,29(3): 84-90.
[4] 张晓光,赵克,孙力,等.永磁同步电动机滑模变结构调速系统新型趋近率控制[J].中国电机工程学报,2011,31(24): 77-82.
[5] 方斯琛,周波,黄佳佳,等.滑模控制永磁同步电动机调速系统[J].电工技术学报,2008,23(8): 29-35.
[6] 曹先庆,朱建光,唐任远.基于模糊神经网络的永磁同步电动机矢量控制系统[J].中国电机工程学报,2006,26(1): 137-141.
[7] 黄庆,黄守道,伍倩倩,等.基于模糊自抗扰控制器的永磁同步电动机伺服系统[J].电工技术学报,2013,28(9): 294-301.
[8] 侯利民,张美金,王巍,等.基于自抗扰控制的永磁同步电动机滑模控制调速系统[J].微特电机,2011,39(4): 50-52.
[9] 张隆,杨俊华,吴捷.基于自抗扰矢量控制的DFIG系统低电压穿越策略[J].电机与控制应用,2015,42(10): 6-11.
[10] SU Y X, ZHENG C H, DUAN B Y. Automatic disturbances rejection controller for precise motion control of permanent-magnet synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2005, 52(3): 814-823.[11] SIRA-RAMIREZ H, LINARES-FLORES J, GARCIA-RODRIGUEZ C, et al. On the control of the permanent magnet synchronous motor: an active disturbance rejection control approach[J]. IEEE Transactions on Control Systems Technology, 2014, 22(5): 2056-2063.
[12] 韩京清.从PID技术到“自抗扰控制”技术[J].控制工程,2002,9(3): 13-18.
[13] 韩京清.自抗扰控制技术-估计补偿不确定因素的控制技术[M].北京: 国防工业出版社,2013.
Application of Adaptive Control Based Active Disturbance Rejection Control for Permanent Magnet Synchronous Motor Control
ZHANGDemin1,2,XUShiyuan1,2
(1. School of Electrical Engineering, Tianjin University of Technology, Tianjin 300384, China; 2. Tianjin Key Laboratory of Control Theory & Applications in Complicated Systems, Tianjin 300384, China)
An adaptive control based on active disturbance rejection control (ADRC) was presented. And the technique to the control of permanent magnet synchronous motor (PMSM) was applied. Simulation experiment showed the validity of this technique. By comparison to the classical PI controller, the velocity of PMSM was smooth and steady, system had better robustness, and cost less control energy.
active disturbance rejection control (ADRC); permanent magnet synchronous motor (PMSM); adaptive control; control energy
张德民(1973—),男,副教授,研究方向为智能控制理论及应用研究、计算机控制系统。 徐仕源(1990—),男,硕士研究生,研究方向为电机控制与电气传动。
TM 301.2
A
1673-6540(2017)04- 0070- 04
2016 -07 -15

