改进自抗扰的永磁同步电机直接转矩控制无传感系统研究*
韩 晔, 厉 虹
(北京信息科技大学 自动化学院,北京 100192)
改进自抗扰的永磁同步电机直接转矩控制无传感系统研究*
韩 晔, 厉 虹
(北京信息科技大学 自动化学院,北京 100192)
针对永磁同步电机直接转矩控制系统低速时传统电压模型对定子磁链估计不准确的问题,采用自抗扰控制技术中的扩张状态观测器对定子磁链和转速进行估计,提高观测精度并实现直接转矩控制系统的无传感器运行;对自抗扰调节器进行改进,简化调节器的结构并引入模糊控制对调节器参数进行优化,减少待整定参数并实现参数的自动调节。将改进的自抗扰调节器替代PI调节器用于速度调节,以提高系统的抗扰性;采用空间电压矢量调制替代传统的开关表和滞环比较器,使功率器件开关频率恒定,减小系统的磁链和转矩的脉动。仿真结果验证了算法的有效性。
永磁同步电机;直接转矩控制;自抗扰控制;扩张状态观测器;空间矢量脉宽调制;模糊控制
0 引 言
直接转矩控制(Direct Torque Control,DTC)是利用逆变器输出的电压矢量直接控制电机定子磁链和电磁转矩的高性能交流电机控制方法[1]。与矢量控制相比,DTC摒弃了解耦的思想,省去了旋转坐标变换,具有结构简单、转矩响应速度快等优点[2]。采用矢量控制或DTC的电机调速系统需要用机械传感器检测电机的转子速度,而机械传感器的使用会增加系统的成本和复杂性,降低系统的可靠性。因此,永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)的无速度传感器技术[3-4]也是近年来的研究热点。对电机转子速度和位置的估计方法可分为适用于中高速的开环估计法[5]、模型参考自适应法[6],适用于低速的高频注入法[7]、卡尔曼滤波法[8],以及适用于转子初始位置估计的INFORM法[9]等。
PMSM具有多变量、非线性、强耦合的特点,要满足其在复杂系统中的应用,必须提高电机性能,克服大负载和多变扰动工况带来的影响。在传统的DTC系统中,采用传统的电压积分法进行磁链估计会出现积分初值难以确定、误差积累、直流信号偏置等问题,尤其是在电机低速运行时反电势很小,对定子磁链难以准确观测;速度反馈采用PI算法,存在系统快速性和超调间的矛盾;滞环比较器只能做出非0即1的判断,无法区分系统偏差的大小,造成逆变器开关频率不恒定;系统运行时,定子电阻值变化造成磁链畸变,导致磁链估计偏差较大。上述问题的存在,使DTC系统输出磁链和电磁转矩脉动较大,抗干扰性能较差,制约了DTC在工程中的应用。
本文设计一种改进的自抗扰控制器(Active Disturbance Rejection Control,ADRC)[10-15],对典型的ADRC结构进行简化,减少待整定参数,并引入模糊控制[16-17]对ADRC的参数进行优化,使控制器具有更强的自适应性。采用改进的ADRC替代PI控制器用于速度调节,减小电机参数变化和负载扰动对系统的影响;采用扩张状态观测器(Extended State Observer,ESO)准确估计系统的磁链和转速,提高系统低速运行时的观测精度;采用空间矢量脉宽调制(Space Vector Pulse Width Modulation,SVPWM)技术[18]替代传统的开关表和滞环比较器,保证逆变器开关频率恒定,抑制DTC系统中输出磁链和转矩的脉动。仿真验证了上述方法的有效性。
1 改进ADRC的速度调节器设计
1. 1 ADRC的数学模型
ADRC主要由三部分组成:非线性跟踪微分器(Tracking Differentiator,TD)、ESO和非线性状态误差反馈(Nonlinear State Error Feedback,NLSEF)。其中TD实现对系统输入信号的快速跟踪,并能从中提取出良好的微分信号;ESO是ADRC的核心,通过ESO的观测可以得到各状态变量的估计值,且能估计出内外扰动的实时作用量并加以反馈和补偿;NLSEF是ESO和TD产生的状态量估计值间误差的非线性组合。
设被控对象数学模型为
(1)
式中:f0,b0——已知部分;f1,b1——未知部分;w(t)——未知扰动;u——控制输入。
一阶ADRC结构如图1所示。

图1 一阶ADRC结构框图
图1中,v是系统输入信号;v1是v的跟踪信号;y是被控对象的输出信号;z1是y的跟踪信号;z2是扰动观测值;b0是补偿因子;z2/b0是用于补偿对象内外扰动的补偿量。u0是经过NLSEF得到的被控对象初始信号;u是经过补偿扰动后得到的最终控制信号。
由于一阶ADRC需要整定的参数较多,且参数的调整过程繁杂,不利于在工程中推广应用。为了降低模型的复杂性并减小控制器的计算量,本文在保留ADRC精华的前提下,对控制器进行改进。
1. 2 改进的ADRC速度调节器设计
PMSM的运动方程为
(2)
式中:Te——电磁转矩;TL——负载转矩;ωr——电机转速;B——摩擦力矩;J——转动惯量。
根据式(2),转速输出方程可写为
(3)
由式(3)可知,负载转矩、转动惯量和摩擦力矩的变化都会对转速控制的精度产生影响,所以将其视为扰动,则式(3)可表示为
(4)
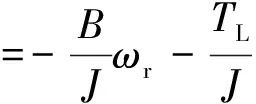
由于TD的主要作用是提取微分信号,但对一阶ADRC而言,ESO只输出系统和观测扰动的跟踪信号,并没有控制对象的微分输出信号,所以TD在系统中只起到了滤波作用。为降低模型复杂性并减少待整定参数,可省略TD。在NLSEF中由于fal函数的特性曲线并不平滑,这种不平滑特性易使系统在进入稳态后产生抖振,故可采用比例增益替代NLSEF部分,便于数字计算的实现,同时加快系统的响应速度。此时,一阶ADRC控制器数学模型如下。
ESO:
(5)
非线性误差反馈控制率:
(6)
式中的fal函数表示为
(7)
在工程应用中,一阶ADRC中NLSEF的误差增益系数β不易调节,在多变扰动工况的条件下,该参数需要进行手动调节,这不利于实际应用。因此,本文将模糊控制用于ADRC的设计中,利用模糊规则对NLSEF中的参数进行整定,达到在线修改参数的目的,有利于ADRC控制器在工程实际中的应用。
模糊控制器的输入为系统给定速度与状态观测器对反馈速度的状态估计值间的误差e和误差变化率ec,输出为NLSEF中待整定参数的修正值Δβ。在它们的论域上均定义7个语言子集,分别为{“正大(PB)”、“正中(PM)”, “正小(PS)”、“零(ZO)”、“负大(NB)”、“负中(NM)”, “负小(NS)”}。取e和ec的论域分别为[-4,+4]、[-15,+15], 隶属度函数选取高斯型;取Δβ的论域为[-0.6,0.6],隶属度函数选取三角形;模糊推理采用Mamdani算法,去模糊化算法采用平均加权法[19]。对Δβ整定的模糊规则如表1所示。

表1 Δβ模糊规则表
去模糊化后,查出修正值Δβ后代入式(8):
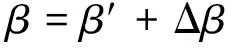
(8)
式中:β′——NLSEF中误差增益的初始值。
改进的自抗扰速度调节器结构如图2所示。

图2 改进的一阶自抗扰速度调节器框图
2 基于ESO的磁链和转速观测器
PMSM DTC无传感系统需要对定子磁链和转速进行准确观测。由于PMSM在αβ坐标系下的定子磁链方程中包含电机的定子磁链和转子位置信息,所以将定子磁链方程作为研究对象,把含磁链和转速的不确定项扩张为新的状态变量,利用ESO进行实时观测,并提取出磁链和转速状态信息,最终实现系统的无传感器运行。
PMSM在两相静止坐标系下的电压方程为
(9)
磁链方程为
(10)
式中:iα、iβ,uα、uβ,ψα、ψβ——定子电流、电压、磁链在α、β轴上的分量;
ψr——转子永磁磁链;
Ls——定子电感;
Rs——定子电阻;
ωr——电机转速;
θr——转子位置角。
由式(9)、式(10)可得
(11)
由于系统实际测量的是定子电流和电压,待估量为定子磁链,因此选输入变量U=[uαuβ]T,输出变量I=[iαiβ]T,状态变量X1=[ψαψβ]T,即可得到状态方程:
(12)
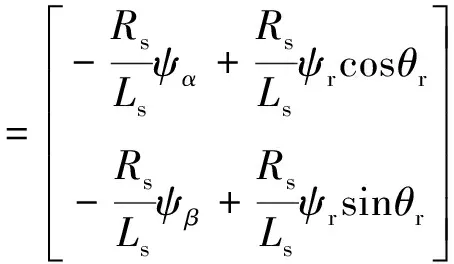
为设计状态观测器,将f(X1)分解成两部分,即:
式中:f1(X1)——线性项;f2(X1)——非线性项。
由于f2(X1)中包含转子位置信息θr,所以将f1(X1)视为系统的已知部分,将f2(X1)视为系统的未知部分并扩张成新的状态变量X2,即有
(13)
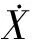
(14)
根据式(14)可构造ESO为
(15)
由式(15)可得定子磁链的实时观测值:
(16)
(17)
(18)
与一些传统的定子磁链和转速估计方法相比,基于ESO的观测方法可将系统中的所有不确定因素都归为未知扰动,只要ESO对扩张项的观测准确,就可以保证磁链和转速的估计准确,减小了电机参数变化和负载扰动对系统的影响,提高了磁链解算和转速估计的准确性。
3 SVPWM DTC系统
表贴式PMSM的转矩方程为
(19)
对式(19)求导可得
(20)
式(20)表明,电机的电磁转矩Te与负载角δ之间存在着非线性关系。当δ很小时,cosδ可近似为1,则Te与δ之间近似为线性关系。所以,用PI调节器可将转矩误差T转化成负载角增量δ,这时,可依据负载角偏差δ、定子磁链位置角θs和给定定子磁链幅值计算出参考定子磁链矢量在αβ坐标上的分量:
(21)
则定子磁链矢量的偏差为
(22)
再结合定子电流和电阻及其采样周期就可以得到预期电压矢量Us及其分量Uα、Uβ的大小:
(23)
(24)
式中:φ——参考电压矢量的位置角。
计算出参考电压矢量后,通过SVPWM算法得到电压矢量间的等效组合。其中,完成SVPWM算法可分为三个步骤,首先要判断出电压矢量所处的扇区,然后推导出电压矢量的通用时间变量,再根据电压矢量的作用时间生成控制信号,最终输出六路脉冲信号驱动逆变器控制电机。
由上述分析可知,在参考定子磁链和参考电压矢量的计算中考虑了电磁转矩和定子磁链的误差,利用SVPWM算法将得到的预期电压矢量表示成基本电压矢量和零电压矢量的优化组合,并以逼近预期电压矢量为目标来确定开关电压矢量的作用时间,最终对磁链和转矩的偏差进行准确补偿,降低系统输出的磁链和转矩脉动。另外,在传统的DTC系统中,滞环比较器环宽的设置范围会影响到逆变器的开关频率,导致开关频率不恒定。SVPWM算法的采样周期恒定,可保证逆变器的开关周期和频率恒定,提高了系统的可靠性。
4 仿 真
基于改进ADRC的PMSM DTC无传感系统结构如图3所示。其中,速度调节采用模糊ADRC,通过ESO对定子磁链和转速准确估计,得到反馈的电磁转矩值和转速估计值。给定电磁转矩和反馈电磁转矩间的误差信号经过PI调节后输出负载角的偏差。根据负载角的偏差、定子磁链位置角及给定磁链的幅值计算出参考定子磁链矢量,以确定预期电压矢量,最终经过SVPWM输出6路控制信号驱动逆变器。

图3 基于改进ADRC的PMSM DTC无传感器系统
在MATLAB/Simulink环境下进行仿真。其中逆变器的直流母线电压Ud=400 V,磁链给定值Ψ*=0.215 Wb。PMSM参数如下:极对数p=4,定子电阻R=2.875,dq轴电感Ld=Lq=8.5 mH,转子磁链Ψf=0.215 Wb,转动惯量J=0.8×10-4kg·m2,摩擦因数B=0。
给定转速为300 r/min、转矩为3 N·m的条件下,转速在0.1 s时从300 r/min突变到600 r/min,转矩在0.25 s时由3 N·m跳变到10 N·m。图4为采用传统DTC系统和改进ADRC的DTC系统得到的定子磁链轨迹。

图4 定子磁链圆波形
图4表明,在传统的DTC系统中,磁链圆有一定的环宽,其半径在0.215 Wb处波动,因此定子磁链的脉动较大。在采用改进ADRC的DTC系统中,定子磁链圆的环宽明显变窄,磁链脉动减小。
图5是相同条件下用传统的电压模型进行定子磁链估计的曲线。
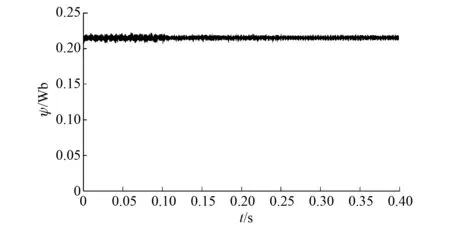
图5 基于电压模型的估计磁链曲线
图6是在相同条件下用ESO观测定子磁链的曲线。
图6 基于ESO的估计磁链曲线
比较图5和图6,ESO对定子磁链的估计比电压模型的估计更加准确,在稳态时磁链脉动更小。这主要是因为ESO对系统扰动的准确估计和补偿。另外,与传统的电压模型相比,ESO的观测没有纯积分环节,不会产生较大的误差积累和直流漂移,也不存在电机低速运行时反电势很小、对定子磁链难以观测的问题,所以在低速时对磁链的估计准确性更高。
图7是在相同条件下采用传统DTC系统和改进ADRC的DTC系统得到的电磁转矩响应曲线。

图7 转矩响应曲线
图7表明,与传统DTC系统相比,当电机运行速度变化时,采用改进ADRC的DTC系统输出的转矩变化更小,转矩脉动也有所减小。这是由于用SVPWM技术替代滞环比较器和开关表,经过优化组合的电压矢量可以对磁链和转矩的偏差进行准确补偿,提高系统的稳态性能;另外,采用ESO对定子磁链的观测更加准确,提高了控制精度,能够更加准确地补偿磁链和转矩的偏差。
图8是在相同条件下采用传统DTC系统和改进ADRC的DTC系统得到的转速响应曲线。
图8表明,传统的DTC系统中,转速超调较大,稳态阶段存在转速脉动,且转速受负载变化的影响明显,稳态误差为2.25%;而改进ADRC的DTC系统中,转速基本无超调,稳态精度高,转速受负载变化的影响更小,稳态误差为0.48%,且恢复时间更短。说明改进的ADRC具有抗干扰能力强、稳定性好的优点。
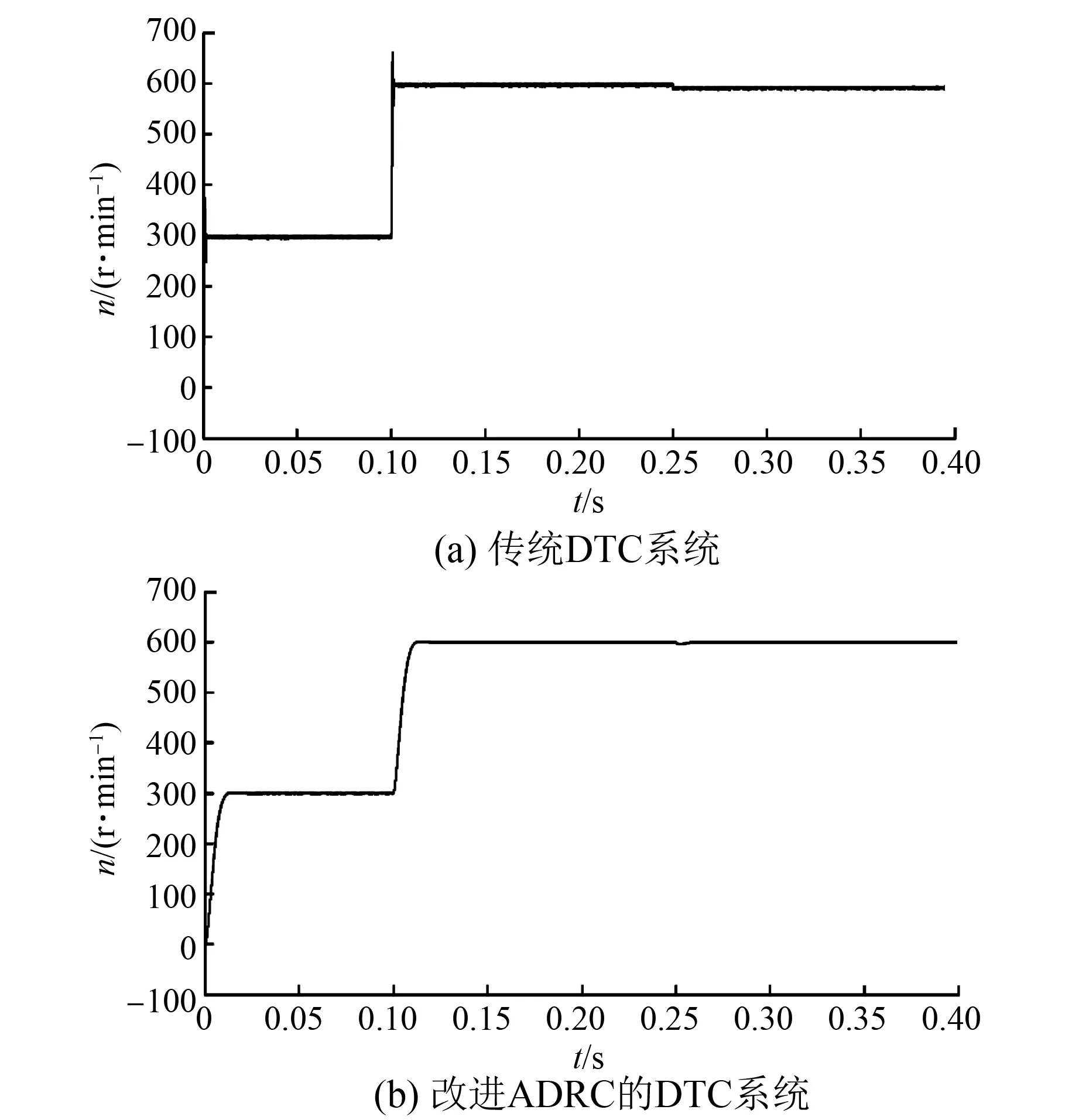
图8 转速响应曲线
同样条件下,改进ADRC的DTC系统中ESO对电机速度的误差观测结果如图9所示。
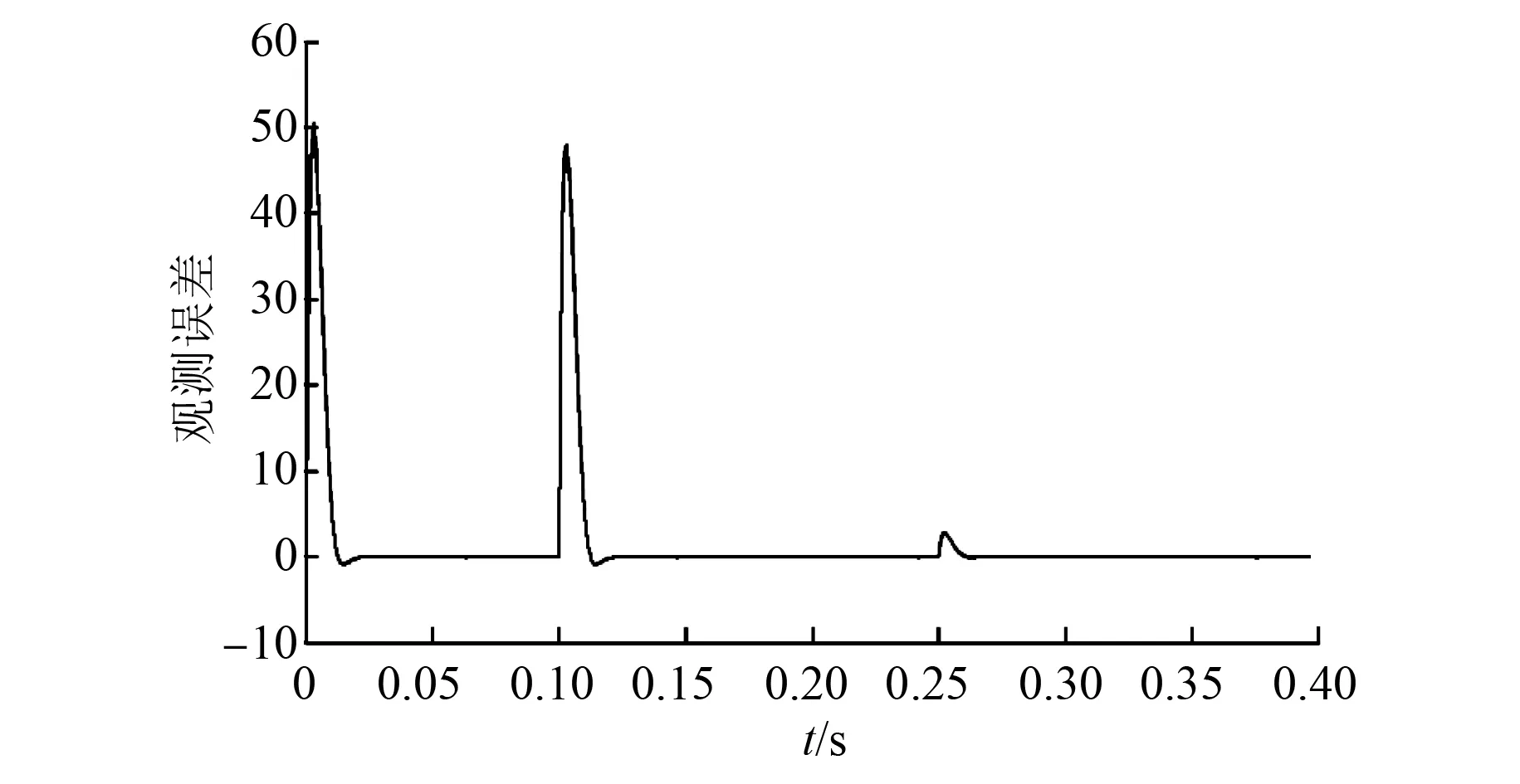
图9 ESO对速度的观测误差
图9表明,ESO对系统速度的状态估计和系统实际速度间的误差很小,说明ESO对系统中的非线性因素和扰动的估计比较精确,验证了ESO实时估计系统内外扰动作用的实用性与有效性。
图10是在给定转速为1 200 r/min、负载为3 N·m的条件下,分别采用常规ADRC和改进ADRC得到的转速响应曲线。

图10 转速响应曲线
图10表明,在电机的速度调节中,采用带状态观测器前馈补偿加模糊控制的一阶ADRC,省略了TD,以线性误差控制率替代NLSEF中的非线性fal函数,减少了控制器待整定参数和系统计算量,降低了模型的复杂性,缩短了系统的调节时间。此外,采用模糊控制对ADRC控制器中NLSEF的参数进行整定,对于不同的外部工况条件,参数无需手动调节,有利于工程应用。
图11是在电机堵转时,在0.1 s突加负载到3 N·m的条件下,传统DTC系统和改进ADRC的DTC系统得到的转速响应曲线。

图11 转速响应曲线
图11表明,改进ADRC的抗干扰能力较PI调节器更强,这主要是由于ADRC中的ESO将系统的负载扰动和电机的参数变化都归为未知扰动,并进行准确的估计和补偿,使系统对负载突变具有很强的抗干扰能力。同时,引入模糊规则对ADRC的参数进行自动调节,在一定范围内优化系统参数,也进一步提高了控制器的自适应性。
图12是在给定转速为400 r/min、负载为4 N·m的条件下,实际转速响应曲线和ESO观测的估计转速响应曲线。

图12 转速响应曲线
图12表明,基于ESO的速度估计方法,估计转速能快速跟踪电机的实际转速,在稳态阶段的速度辨识误差约为0.4 r/min,稳态精度较高,说明ESO的转速估计方法准确。这主要是因为基于ESO速度观测的方法受电机参数变化的影响小,并可以对系统扰动进行有效补偿,所以转速估计准确性较高。
图13是在相同条件下转子的实际位置和ESO观测得到的转子估计位置曲线。

图13 转子位置
图13表明,ESO速度观测器估计的转子位置与电机转子的实际位置比较接近,说明这种观测方法能减小电机参数变化和负载扰动对系统转速估计的影响,在电机低速稳态运行时对转子位置的估计是准确的。
5 结 语
本文设计了基于改进ADRC的PMSM DTC无传感系统。系统采用改进的模糊自抗扰速度调节器替代PI调节器,提高了调节器的自适应性和系统的抗干扰能力;引入ESO对定子磁链和转速进行更准确的观测,并实现系统的无传感运行,与传统的电压模型相比,提高了磁链解算的准确性;采用SVPWM技术替代传统的开关表和滞环比较器,有效降低磁链和转矩脉动。仿真验证了控制策略的有效性,为PMSM DTC无速度传感器系统的转速估计提供了可行的思路。
[1] 杨建飞,胡育文.永磁同步电机最优直接转矩控制[J].中国电机工程学报,2011,31(27): 109-115.
[2] 高靖凯,林荣文,张润波.永磁同步电机直接转矩控制的研究及算法改[J].电机与控制应用,2015,42(11): 16-20.
[3] 李君,李毓洲.无速度传感器永磁同步电机的SVM-DTC控制[J].中国电机工程学报,2007,27(3): 28-34.
[4] JANISZEWSKI D. Sensor less control of permanent magnet synchronous motor based on Kalman filter[J]. Power Engineering, Energy and Electrical Drives, 2011(1): 11-13.
[5] 吴奇,程小华.永磁同步电机的无传感器控制策略[J].电机与控制应用,2009,36(8): 29-32.
[6] 张伯泽,阮毅.基于MRAS内置式永磁同步电机无位置传感器控制研究[J].电机与控制应用,2016,43(4): 13-16.
[7] 缪学进,李永东,肖曦.高频信号注入无速度传感器永磁同步电机控制系统[J].电气传动,2007,37(3): 11-14.
[8] 于信忠,张承瑞,李虎修,等.基于自适应扩展卡尔曼滤波器的永磁同步电机超低速控制[J].电机与控制应用,2012,39(9): 24-29.
[9] 刘颖,周波,李帅,等.转子磁钢表贴式永磁同步电机转子初始位置检测[J].中国电机工程学报,2011,31(18): 48-54.
[10] 韩京清.自抗扰控制技术[M].北京:国防工业出版社,2008.
[11] 李婉婷,厉虹.永磁同步电机自抗扰控制技术研究[J].电气传动,2015,45(9): 20-24.
[12] 刘英培.一种永磁同步电机直接转矩控制无传感运行优化方法[J].中国电机工程学报,2014,34(30): 5368-5377.
[13] 刘英培,栗然,梁海平.基于最小二乘支持向量机优化自抗扰控制器的永磁同步电机直接转矩控制方法[J].中国电机工程学报,2014,34(27): 4654-4664.
[14] 邵立伟,廖晓钟,张宇河,等.自抗扰控制在永磁同步电机无速度传感器调速系统的应用[J].电工技术学报,2006,21(6): 35-39.
[15] 顾问,王久和.基于自抗扰控制的永磁同步电机矢量控制策略[J].电源学报,2011,9(5): 65-68.
[16] 薛薇,路鸦立.永磁同步电机调速系统的模糊自抗扰控制[J].电机与控制应用,2013,40(8): 57-65.
[17] 于金鹏,陈兵,于海生,等.基于自适应模糊反步法的永磁同步电机位置跟踪控制[J].控制与决策,2010,25(10): 1547-1551.
[18] 陈振,刘向东,戴亚平,等.采用预期电压矢量调制的PMSM直接转矩控制[J].电机与控制学报,2009,13(1): 40-46.
[19] 黄庆,黄守道,伍倩倩,等.基于模糊自抗扰控制器的永磁同步电动机伺服系统[J].电工技术学报,2013,28(9): 294-301.
Research on Permanent Magnet Synchronous Motor Direct Torque Control Sensorless System Based on Improved Active Disturbance Rejection*
HANYe,LIHong
(School of Automation, Beijing Information Science & Technology University, Beijing 100192, China)
To solve ripples on stator flux linkage when using traditional voltage model to estimate at low speed in the direct torque control (DTC) of permanent magnet synchronous motor (PMSM) system. The stator flux and rotor speed were estimated by the extended state observer (ESO) of the active disturbance rejection control (ADRC) technique, and the sensorless speed control had been realized. The structure of the ADRC controller was simplified and fuzzy control was introduced to optimize the parameters of the controller. In the DTC system, the improved ADRC regulator was used to replace the PI regulator for speed regulation, and the anti-interference ability of the system was improved. The space vector pulse width modulation (SVPWM) instead of the traditional selecting table and hysteresis comparator, the switching frequency constant and the ripples on flux linkage and torque had been reduced. Simulation results verified the effectiveness of this algorithm.
permanent magnet synchronous motor (PMSM); direct torque control (DTC); active disturbance rejection control (ADRC); extended state observer (ESO); space vector pulse width modulation (SVPWM); fuzzy control
国家自然科学基金项目(11472058)
韩 晔(1991—),男,硕士研究生,研究方向为交流电机非线性控制。 厉 虹(1959—),女,教授,研究方向为高性能电气传动控制系统。
TM 351
A
1673-6540(2017)04- 0052- 08
2016 -10 -24

