污染源位置对圆柱形水工建筑下游污染物浓度分布的影响

武玉涛,任华堂,夏建新

(中央民族大学生命与环境科学学院,北京 100081)



污染源位置对圆柱形水工建筑下游污染物浓度分布的影响

武玉涛,任华堂,夏建新

(中央民族大学生命与环境科学学院,北京 100081)

利用雷诺方程和RNGk-ε紊流模型,对排放源在圆柱形水工建筑上游和下游两种工况下的尾流浓度场进行数值模拟,从污染物时均浓度、浓度脉动强度和浓度半宽度3个方面比较了污染源位置对圆柱形水工建筑下游污染物浓度分布特性的影响。结果表明:随流程的增大,两种工况下污染物时均浓度横向断面分布先后经历双峰结构、过渡阶段和高斯分布3个阶段;排放源在上游时,浓度脉动强度先增大后减小;排放源在下游时,浓度脉动强度一直减小;两种工况的浓度半宽度变化规律一致,当1≤x/D<15时浓度半宽度呈非线性增长,当15≤x/D≤30时呈线性增长。

圆柱绕流;雷诺方程;数值模拟;浓度分布;尾流

桥墩、高柱等圆柱形水工建筑会对其上下游的污染源产生截然不同的影响。污染源位于上游,污染物输移至水工建筑位置时会随水流向建筑物两侧迁移,横向影响范围快速扩展;而污染源位于下游,建筑物后方由于圆柱绕流形成的负压作用,污染物将会长期滞留难以扩散至外围。因此,污染源位置不同会导致圆柱形建筑物周边污染物浓度分布出现明显的差异。在水环境治理中,需要根据污染源所处的位置制定针对性的处理措施；同时,在桥墩或圆形岛屿附近的排污口选址需要考虑水流方向和水工建筑位置进行科学设计。研究污染源位置和圆柱形水工建筑后方浓度场分布之间的响应关系对于水环境保护和工程设计具有重要的理论意义和现实意义。

近年来,关于河口海岸附近污染物在水动力作用下输移扩散规律的研究[1-2]屡见报道，但对于河口海岸建设的桥墩、高柱等圆柱形水工建筑对浓度场分布影响的研究尚不多见。Balachandar等[3-4]通过物理模型试验,测量了污染源位于平板下游时,尾流区浓度分布的不均匀特性,发现浓度峰值可达平均浓度的数倍。梁东方等[5-6]利用平面激光诱导荧光技术(PLIF)定量测量了污染源在圆柱上游5D(D为圆柱直径)处时圆柱下游较近断面的污染物浓度分布,结果表明时均浓度分布呈现明显的双峰结构,但浓度的峰值仅稍大于平均浓度。Chen等[7]研究发现排放源的位置对海岬浅水尾流区污水的滞留时间和浓度分布有重要影响。晏智锋[8]采用数学模型模拟了污染源在上游5D处时单圆柱和多圆柱的污染物浓度场,结果显示不同浅水尾流系数条件下尾流中污染物浓度横向分布可以表现为双峰分布结构和正态分布结构。这些研究成果均揭示了特定污染源位置条件下圆柱体周围的污染物浓度分布特性。由于问题的复杂性,目前研究成果多为污染物绕流现象的测量和特征的定性描述,缺少对圆柱绕流过程中污染物迁移扩散的内在原因揭示和定量分析,对于不同污染源位置条件下圆柱形水工建筑下游污染物迁移扩散特性比较系统的研究尚未见报道。

本文基于FLUENT软件平台,在雷诺数Re=3 900条件下,利用雷诺时均的N-S方程和RNGk-ε紊流模型,在排放源分别位于圆柱上、下游条件下进行污染物浓度场的数值模拟,比较不同点源位置对各个断面上污染物的时均浓度、浓度脉动强度、浓度半宽度的影响,以对圆柱形水工建筑附近的水环境保护和工程设计提供参考。

1 数学模型及数值方法

1.1 控制方程

水动力控制方程为雷诺时均的N-S方程：

(1)

(2)

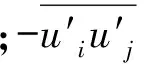
采用对流扩散方程模拟尾流区污染物输移扩散规律:

(3)

式中:C为污染物质量浓度;μt为紊流涡黏系数;Pr为Prandtl数,Pr=0.7;Dm为污染物的背景扩散系数;S为源项。

紊流模型采用RNGk-ε紊流模型[9]:

(5)

式中:k为湍动能；ε为湍动能耗散率；Gk为平均速度梯度引起的湍动能生成率；μeff为有效紊流黏性系数;αk=αε≈1.393;C1=1.42;C2=1.68。

1.2 数值试验条件与模型验证

a. 计算区域。圆柱绕流的数值试验区域如图1所示,圆柱直径为D(半径记为R),入口边界距离圆柱前滞点的距离为10D,上下边界距离圆柱为10D,出口边界设置在柱后30D处。设置3种工况：工况1的污染源位于圆柱前方5D处(x/D=-5,y/D=0);工况2的污染源位于圆柱后方0.6D处(x/D=0.6,y/D=0);工况3作为对照,将工况1中的圆柱去掉。

图1 计算区域

采用四边形结构网格,在计算区域上下边界各对称布置290个节点,左右边界各对称布置160个节点,圆柱壁面等间距布置160个节点,计算域单元数为48 480,计算区域单元和圆柱周边单元划分如图2所示。

图2 网格划分

b. 边界条件。入口设置为速度入口边界,设定雷诺数为3 900,相应的流速u0=0.39 m/s;上、下边界设置为对称边界;圆柱表面设置为无滑移壁面条件;出口边界设置为自由出流边界;3种工况条件下污染源均为垂向连续点源,且均保持污染物通量一致,质量浓度均为0.039 kg/m3。

c. 离散方法和计算参数。对控制方程采用有限体积法(FVM)进行离散,对流项的离散项采用二阶迎风格式,压力与速度耦合的求解采用SIMPLE算法。残差收敛标准为1.0×10-3,时间步长设置为0.002 s。

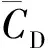
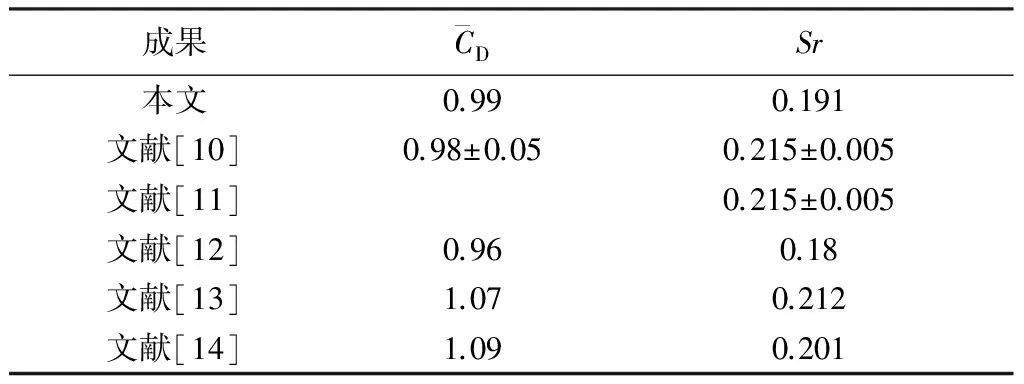
表1 特征参数模拟结果对比

2 模拟结果及分析

2.1 周期平均浓度的分布

2.1.1 污染源下游中心线上的浓度沿程分布

定义相对周期平均浓度Cave为

(6)

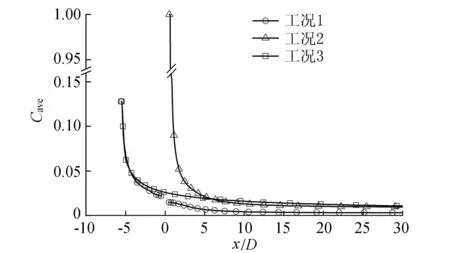
图3 中心线上(y/D=0)的浓度沿程分布

图3为污染源分别位于圆柱上、下游及无障碍物存在3种工况下中心线上的相对浓度分布。由于3种工况条件下污染物源处浓度通量一致,工况1、3污染源处的流速较大,故污染物绝对浓度值较低;而工况2污染源位于圆柱后方负压区,流速较小,故绝对浓度值较高。结果显示,当x/D<5时,污染源在圆柱体下游时,尾流区浓度较高,说明圆柱后方的负压对污染物有富集作用;当x/D>5时,相较于无障碍物存在的水域,工况1和工况2均显示圆柱体的存在加快了沿程浓度值的衰减,这是因为圆柱绕流产生了剧烈的流体扰动和尾流旋涡运动,促进了污染物在横向的输移和扩散。

2.1.2 圆柱下游断面浓度分布

图4为工况1、2条件下各断面的相对周期平均浓度分布。在靠近圆柱体的断面,由于卡门涡衔的剧烈作用呈现出明显的双峰结构,随着x/D的增大,在过渡阶段双峰结构逐渐消失,浓度在横向上的分布趋于均匀化。当x/D足够大时,各断面上的浓度呈高斯分布。

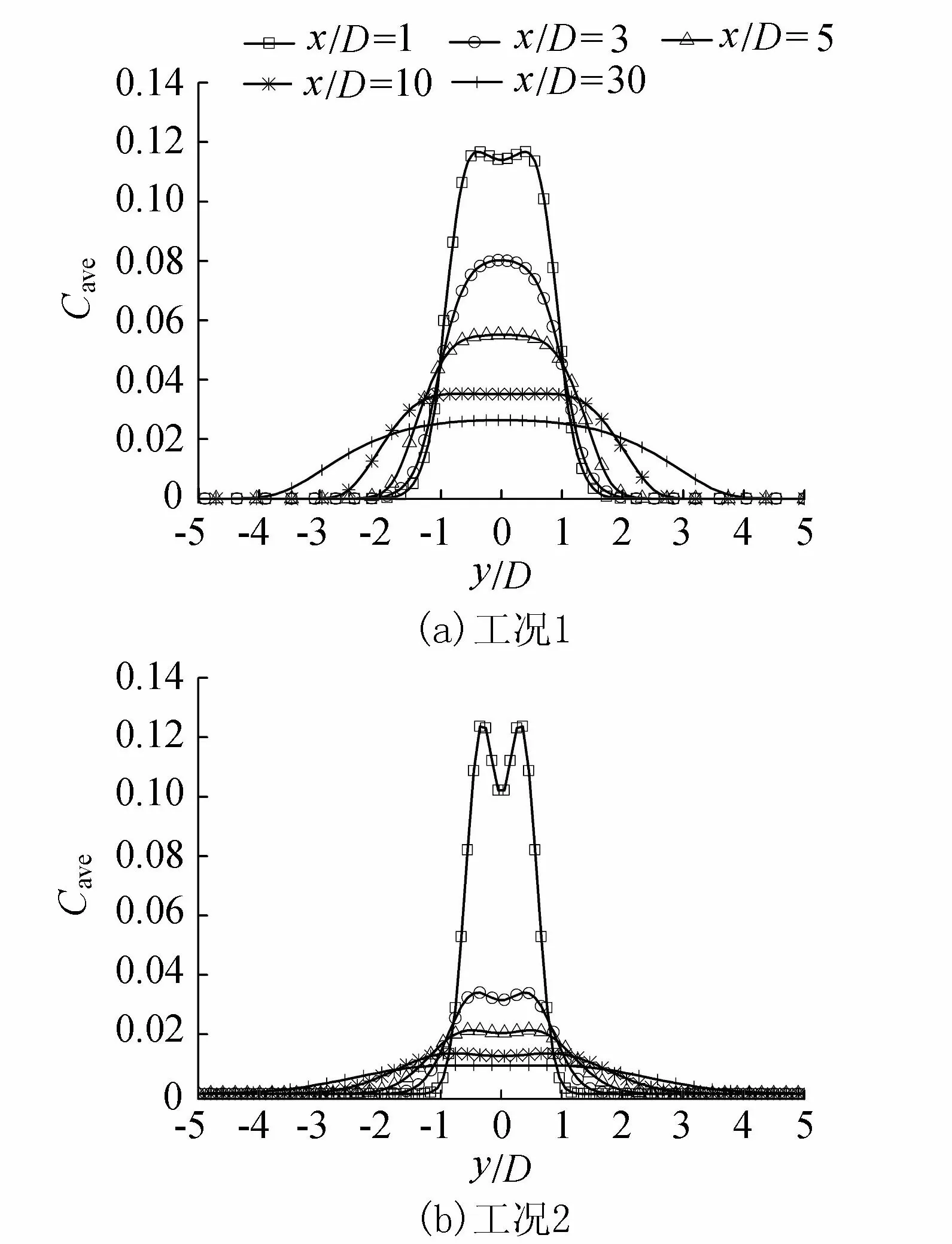
图4 圆柱下游断面相对周期平均浓度分布

比较图4可以看出,在相同的污染源强条件下,在旋涡形成的负压区内的x/D=1断面,工况1比工况2的浓度要小,而之后的各个断面,工况1比工况2的浓度要大。工况2污染物浓度衰减速度较快是因为大部分污染物滞留在圆柱后方的负压区,仅有小部分污染物随旋涡迁移到下游,导致点源在下游时圆柱附近断面的污染物浓度很高,而远离圆柱断面的浓度较低。

当污染源的位置处于圆柱尾流的负压区时,由于旋涡强烈的回流作用,将污染物牢牢锁定在圆柱附近,旋涡可以看作是相对封闭的系统,与主流水体的物质交换很小,导致了浓度场的不均匀性。随着旋涡不断地脱落,旋涡夹带着大量的污染物向下游扩散,同时涡能量的不断减小,使得旋涡对污染物的束缚能力降低,因此加快了污染物的衰减速度。当点源在圆柱上游时,污染物从两侧流经圆柱体会有一定程度的混掺作用,使圆柱后方污染物浓度分布得更加均匀。

2.2 浓度脉动强度的分布

定义浓度脉动强度KC为

(7)

各断面的浓度脉动强度分布情况如图5所示。由图5可见,各个断面上的浓度脉动强度都呈明显的双峰结构。因为尾流区与主流区的边界是随着尾流的周期性摆动而不断变化的,导致在边界附近污染物浓度时大时小,脉动强度较大。当点源位于上游时,由于圆柱体的阻碍及其导致的横向掺混作用,x/D=1断面的浓度脉动强度很小,随着x/D的增大,浓度脉动强度先增加后减小,并在x/D=3时达到最大值,此时KC=2.68。当点源在下游时,在x/D=1时取得最大值,此时KC=4.33,随着污染物远离圆柱,KC值一直减小。x/D=30断面的浓度脉动强度接近于零,表明当x/D≥30时断面的浓度分布不再随时间发生变化,圆柱导致的尾流横向摆动作用消失,瞬时的浓度分布可以近似为时均浓度分布。

图5 浓度脉动强度分布

2.3 下游不同断面污染物横向影响范围

为了衡量污染物在下游不同位置的横向影响范围,引入尾流浓度半宽度的概念,尾流浓度半宽度b1/2,C指横向断面上自尾流中心线至断面质量浓度为最大周期平均值的1/2处的距离。图6给出了3种工况下浓度半宽度的沿程变化。由图6可见,圆柱不存在的情况下,浓度半宽度随着x/D的增加,呈线性增加。由于圆柱的影响,当1≤x/D<3时,点源在上游的浓度半宽度增长缓慢,但其值均高于点源在下游的情况。原因是污染物需要先流经圆柱体,在圆柱体导致的混掺作用下,扩大了污染物的影响范围,并使浓度分布均匀化。当3≤x/D≤30时,点源在上游与点源在下游的浓度半宽度增长情况一致,点源在上游的值略高一些。

图6 浓度半宽度

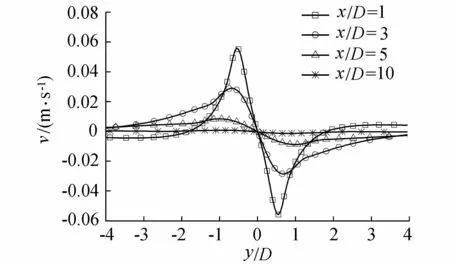
图7 各断面横向速度分布

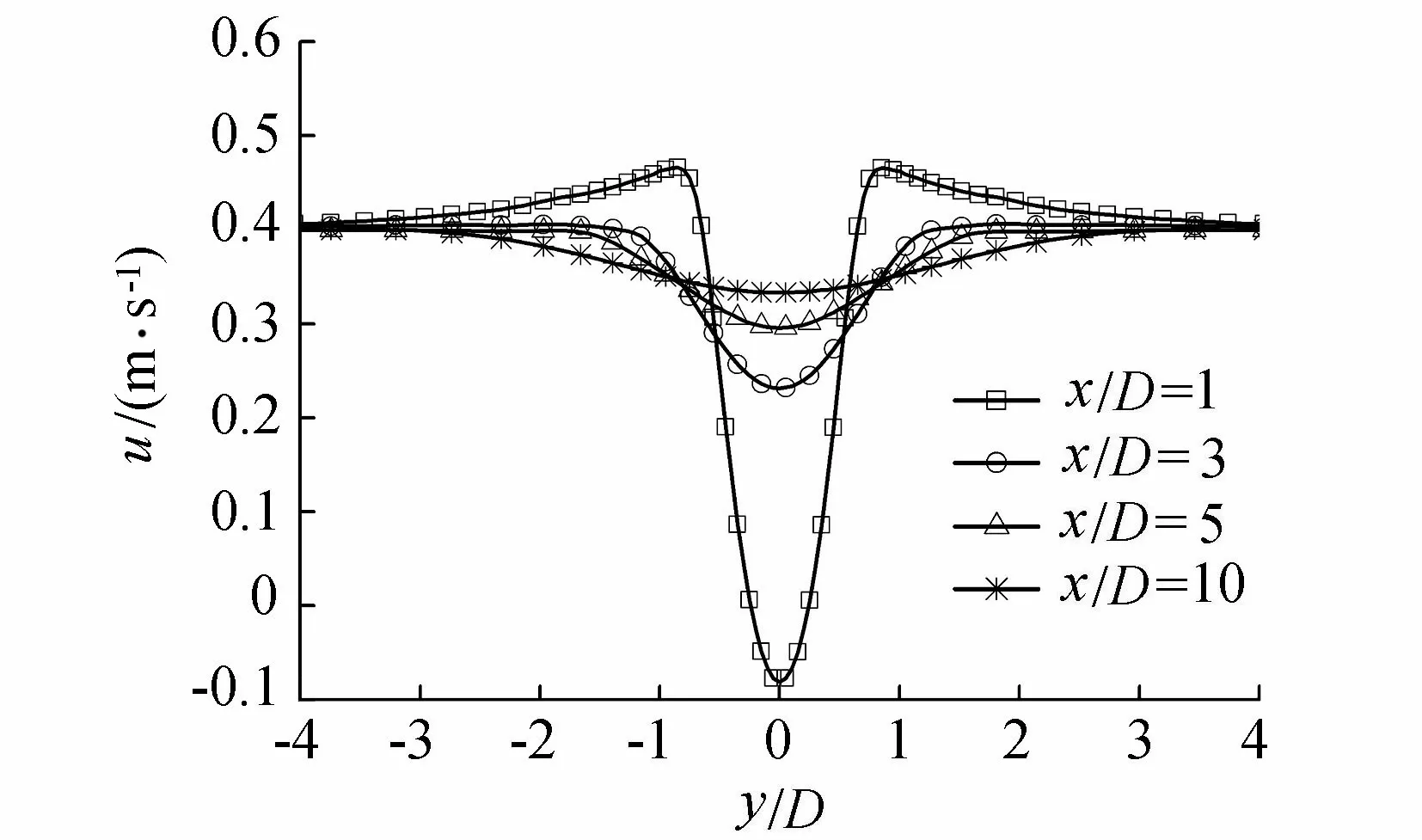
图8 各断面纵向速度分布

为了揭示圆柱横向影响范围的物理机制,图7和图8分别给出了各断面上横向和纵向的流速分布。由于尾流旋涡摆动的影响,流场在横向和纵向上都表现出分布的不均匀性。流场的不稳定直接影响到污染物的浓度分布特性,从而影响污染物的浓度半宽度。点源位于圆柱上游和下游的浓度半宽度方面沿程变化规律一致。当1≤x/D<15时,在横向和纵向速度梯度的作用下,浓度半宽度沿程呈非线性增长;由图7可知,当15≤x/D≤30时横向速度几乎可以忽略,此时浓度半宽度仅受到纵向速度梯度的影响,与x/D线性相关。因此,浓度半宽度在靠近圆柱的区域受到的影响较大,增长较快,而距离圆柱较远的区域受到的影响较小,与无圆柱的情况一样呈线性增长。

根据数值模拟结果(图9)得到当3≤x/D<15时尾流浓度半宽度与x/D的关系满足下式：

(8)

由式(8)可知，b1/2,C与x1/2成正比。

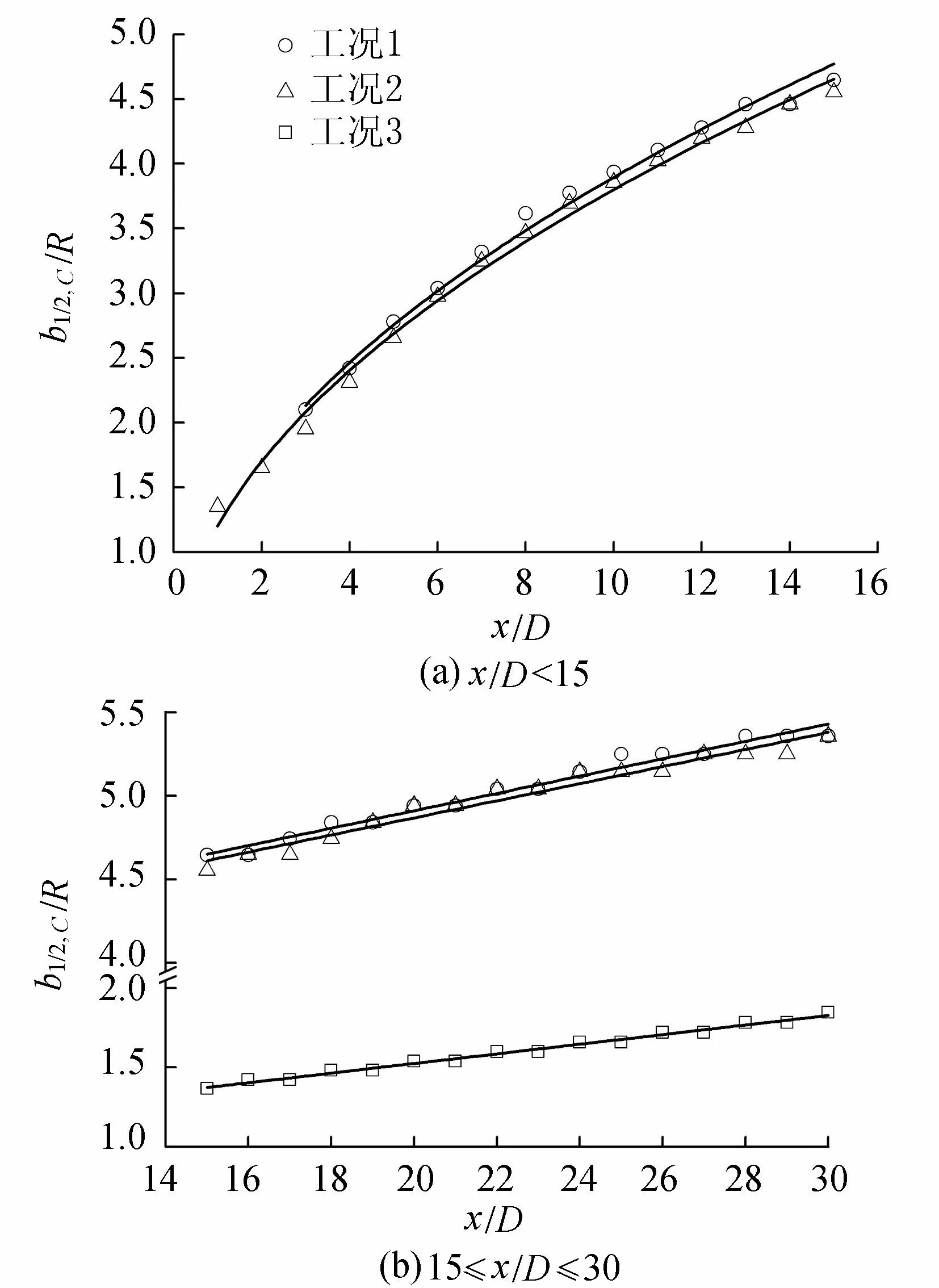
图9 浓度半宽度的拟合曲线

随x/D的增大,在远离圆柱的区域(即15≤x/D≤30)3种工况的尾流浓度半宽度与x/D呈线性关系。可以预见,当x/D的值足够大时,3条线的斜率将保持一致。

Reichardt研究结果表明,圆柱尾流速度半宽度bV随距离变化满足下式[15]:

(9)

对照式(8)(9)可以看出浓度半宽度与纵向速度半宽度之间的关系为

b1/2,C=abV

(10)

式中a为系数。

3 结 论

a. 工况1、2污染物时均浓度的分布均随x/D的增大而增大,沿程经历双峰结构、过渡阶段和高斯分布3个阶段。

b. 浓度脉动强度的计算结果显示,工况1、2浓度脉动强度均呈典型的双峰结构。当点源在上游时,随着x/D的增大,浓度脉动强度先增加后减小,在x/D=3处取得最大值;当点源在下游时,浓度脉动强度一直减小。

c. 当1≤x/D<3时,点源在上游时浓度半宽度沿程增长缓慢,但其值均高于点源在下游的情况;当3≤x/D≤30时,工况1、2的浓度半宽度沿程增长情况一致,与纵向速度半宽度之间满足b1/2，C=abV。且当3≤x/D<15时,浓度半宽度的增长满足b1/2,C∝x1/2;当15≤x/D≤30时,呈线性增长。

[1] 韩龙喜,易路,刘军英,等.连云港近岸海域污染物输移规律[J].河海大学学报(自然科学版),2011,39(3):248-253.(HAN Longxi,YI Lu,LIU Junying,et al.Transport laws for pollutants in coastal area of Lianyungang City[J].Journal of Hohai University (Natural Sciences),2011,39(3):248-253.(in Chinese))

[2] 路川藤,黄华聪,钱明霞.长江口北槽丁坝坝田区潮流及污染物迁移扩散特征[J].河海大学学报(自然科学版),2016,44(3):265-271.(LU Chuanteng,HUANG Huacong,QIAN Mingxia.Tidal current and pollutant diffusion characteristics in spur dike field of North Passage in Yangtze Estuary[J].Journal of Hohai University (Natural Sciences),2016,44(3):265-271.(in Chinese))

[3] BALACHANDAR R,CHU V H,ZHANG J.Experimental study of turbulent concentration flow field in the wake of a bluff body[J].Journal of Fluids Engineering,1997,119(2):263-270.

[4] BALACHANDAR R,TACHIE M F,CHU V H.Concentration profiles in shallow turbulent wakes[J].Journal of Fluids Engineering,1999,121(1):34-43.

[5] 梁东方,李玉梁,江春波,等.岛屿尾流近区浓度的分布特性[J].清华大学学报(自然科学版),2001,51(8):117-120.(LIANG Dongfang,LI Liangyu,JIANG Chunbo,et al.Concentration field in near wakes[J].Journal of Tsinghua University(Science and Technology),2001,51(8):117-120.(in Chinese))

[6] 梁东方,李玉梁,陈嘉范.半岛浅水尾流近区流动特性的试验研究[J].自然科学进展,2004,14(4):431-435.(LIANG Dongfang,LI Liangyu,CHEN Jiafan.Experiment research of peninsula characteristics near wake flow in the shallow water area[J].Progress in Natural Science,2004,14(4):431-435.(in Chinese))

[7] CHEN D,TANG F E,CHEN C.Pollutant trapping at a coastal headland[J].Journal of Waterway Port Coastal & Ocean Engineering,2005,131(3):98-114.

[8] 晏智锋.浅水尾流流动特征及污染物输移扩散特性研究[D].北京:清华大学,2010.

[9] FLUENT Inc.FLUENT 6.3 user’s guide[R].Lebanon: New Hampshire,2006.

[10] NORBERG C.Effects of Reynolds number and a low-intensity freestream turbulence on the flow around a circular cylinder[R].Gothenburg:Department of Applied Thermosdynamics and Fluid Mechanics,Chalmers University of Technology,1987.

[11] ONG L,WALLACE J.The velocity flied of the turbulent very near wake of a circular cylinder[J].Experiments in Fluids,1996,20:441-453.

[12] 于定勇,崔肖娜,唐鹏.并列双圆柱绕流的水动力特性研究[J].中国海洋大学学报(自然科学版),2015,45(5):107-113.(YU Dingyong,CUI Xiaona,TANG Peng.Hydrodynamic characteristics of viscous flow past two side-by-side cylinders[J].Periodical of Ocean University of China,2015,45(5):107-113.(in Chinese))

[13] KRAVCHENKO A G,MOIN P.Numerical studies of flow over a circular cylinder atReD=3 900[J].Physics of Fluids,2000,12(2):403-417.

[14] KIM S E.Large eddy simulation of turbulent flow past a circular cylinder in subcritical regime[C]//Aiaa Aerospace Sciences Meeting & Exhibit.Renoi:[s.n],2006.

[15] 窦国仁.紊流力学:下册[M].北京:高等教育出版社,1987.

Effects of pollution source location on distribution of pollutant concentration downstream of cylindrical hydraulic structure//

WU Yutao, REN Huatang, XIA Jianxin

(CollegeofLifeandEnvironmentalSciences,MinzuUniversityofChina,Beijing100081,China)

The wake concentration fields of a cylindrical hydraulic structure with different pollution source locations (upstream and downstream of the structure) were simulated using the Reynolds equation and RNGk-εturbulence model. The effects of pollution source locations on the distribution of pollutant concentration downstream of the cylindrical hydraulic structure were investigated from three aspects: the time-averaged pollutant concentration, the fluctuation intensity of concentration, and the half-concentration width, which is the distance from the central line of the wake flow to the position with half of the maximum concentration. The results show that with the increase of flow path length, the transverse distribution of time-averaged pollutant concentration experienced three stages, i.e., the bimodal structure, transition stage, and Gaussian distribution. When the pollution source was located upstream, the concentration fluctuation intensity first increased and then decreased; when the pollution source was located downstream, the concentration fluctuation intensity decreased continuously. The variation of the half-concentration width shows the same trends for the two pollution source locations: a nonlinear increase trend when 1≤x/D<15 and a linear increase trend when 15≤x/D≤30.

flow around circular cylinder; Reynolds equation; numerical simulation; concentration distribution; wake flow

国家自然科学基金(51479218);一流大学与一流学科建设过渡性经费专项(1031-01601205)

武玉涛(1991—),男,硕士研究生,主要从事水利工程研究。E-mail:yutaowu2010@163.com

任华堂(1976—),男,副教授,博士,主要从事水利工程研究。E-mail:renhuatang@muc.edu.cn

10.3880/j.issn.1006-7647.2017.03.008

TV131.4

A

1006-7647(2017)03-0049-06

2016-06-22 编辑：郑孝宇)